\n", + "Why did I created a session to plot the graph?
\n", + "[Ans]" + ] + }, + { + "metadata": { + "id": "P3-iuxE4sjAf", + "colab_type": "code", + "colab": {} + }, + "cell_type": "code", + "source": [ + "# Let's define the placeholders\n", + "\n", + "# Placeholders?\n", + "# The input to the model changes on iteration\n", + "# So we cannot have a constant in the input as we did before\n", + "# And thus we need placeholders which we can change on each \n", + "# iteration of the training\n", + "\n", + "x = tf.placeholder(tf.float32, name='x')\n", + "y = tf.placeholder(tf.float32, name='y')" + ], + "execution_count": 0, + "outputs": [] + }, + { + "metadata": { + "id": "8hPRkaoxvRyV", + "colab_type": "code", + "colab": {} + }, + "cell_type": "code", + "source": [ + "# Let's define the linear regression model\n", + "\n", + "# tf.Variable?\n", + "# We define the model parameters as tf.Variables\n", + "# as they get updated throghout the training.\n", + "# And variables denotes something which changes overtime.\n", + "\n", + "W = tf.Variable(0.0, name='weight_1')\n", + "b = tf.Variable(0.0, name='bias_1')\n", + "\n", + "pred_y = (W*x) + b" + ], + "execution_count": 0, + "outputs": [] + }, + { + "metadata": { + "id": "cSw1P8bkv96r", + "colab_type": "code", + "colab": {} + }, + "cell_type": "code", + "source": [ + "# Let's define the loss function\n", + "# We are going to use the mean squared loss\n", + "loss = tf.reduce_mean(tf.square(y - pred_y))" + ], + "execution_count": 0, + "outputs": [] + }, + { + "metadata": { + "id": "5G4uQqjsygNj", + "colab_type": "code", + "colab": {} + }, + "cell_type": "code", + "source": [ + "# Let's define the optimizer\n", + "# And specify the which value (i.e. loss) it has to minimize\n", + "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)" + ], + "execution_count": 0, + "outputs": [] + }, + { + "metadata": { + "id": "ttI7ZT-ozAm1", + "colab_type": "code", + "colab": { + "base_uri": "https://localhost:8080/", + "height": 721 + }, + "outputId": "d0ff4839-1198-44d8-bd4d-79d92dc1a528" + }, + "cell_type": "code", + "source": [ + "# So the graph is now built\n", + "# Now let's execute the graph using session\n", + "# i.e. lets train the model\n", + "\n", + "# What it is to train a model?\n", + "# To update the paramters in the graph (i.e. tf.Variables)\n", + "# So that the loss is minimized\n", + "\n", + "# Okay let's start!\n", + "with tf.Session() as sess:\n", + " # We need to initialize the variables in our graph\n", + " sess.run(tf.global_variables_initializer())\n", + " \n", + " for epoch in range(n_epochs):\n", + " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n", + " \n", + " if epoch % interval == 0:\n", + " print ('Loss after epoch', epoch, ' is ', curr_loss)\n", + " \n", + " print ('Now testing the model in the test set')\n", + " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n", + " \n", + " print ('The final loss is: ', final_loss)\n", + " \n", + "# Plotting the final predictions against the true predictions\n", + "plt.plot(test_X[:10], test_Y[:10], 'g', label='True Function')\n", + "plt.plot(test_X[:10], final_preds[:10], 'r', label='Predicted Function')\n", + "plt.legend()\n", + "plt.show()" + ], + "execution_count": 20, + "outputs": [ + { + "output_type": "stream", + "text": [ + "Loss after epoch 0 is 48290.105\n", + "Loss after epoch 50 is 29.782778\n", + "Loss after epoch 100 is 29.7724\n", + "Loss after epoch 150 is 29.762121\n", + "Loss after epoch 200 is 29.751879\n", + "Loss after epoch 250 is 29.741611\n", + "Loss after epoch 300 is 29.731339\n", + "Loss after epoch 350 is 29.721113\n", + "Loss after epoch 400 is 29.710855\n", + "Loss after epoch 450 is 29.700636\n", + "Loss after epoch 500 is 29.690397\n", + "Loss after epoch 550 is 29.680191\n", + "Loss after epoch 600 is 29.66994\n", + "Loss after epoch 650 is 29.65969\n", + "Loss after epoch 700 is 29.6495\n", + "Loss after epoch 750 is 29.639277\n", + "Loss after epoch 800 is 29.629047\n", + "Loss after epoch 850 is 29.618847\n", + "Loss after epoch 900 is 29.608654\n", + "Loss after epoch 950 is 29.598469\n", + "Now testing the model in the test set\n", + "The final loss is: 33.011585\n" + ], + "name": "stdout" + }, + { + "output_type": "display_data", + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAFKCAYAAADMuCxnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XdYU3cfBfCThBlAluBA1FYtbhHt\n6+pQHNU6ahUVZ7WOundx7713cW9xW6rWWluVqrVaFbWOCooDHChTICGEJPf9I4pVERACNyHn8zx9\nCubm5ptfKcfc5J4rEQRBABEREYlKKvYARERExEAmIiIyCgxkIiIiI8BAJiIiMgIMZCIiIiPAQCYi\nIjICFmI+eExMcr7u39lZjoQEZb4+RmHHNTQMrqNhcB3zjmtoGLldRzc3h3feVqhfIVtYyMQeweRx\nDQ2D62gYXMe84xoaRn6sY6EOZCIiIlPBQCYiIjICDGQiIiIjwEAmIiIyAgxkIiIiI8BAJiIiMgIM\nZCIiIiOQo2IQlUqFVq1aYeDAgahXrx7GjRsHjUYDCwsLLFiwAG5ubqhSpQp8fHwy7rN582bIZKZ3\nvtuKFUsQFvYv4uPjoFKpULKkB4oUccTs2QsMsn8/v9Zwdy8GqfTV34VWrlyb5/2eOfMH6tSpj6Sk\n59iwYQ0CAibkeZ9ERFRwchTIgYGBcHR0BAAsXboUHTt2xJdffokdO3Zg06ZNCAgIgL29PbZt25av\nwxaEIUNGAACOHDmEu3cjMHjwcIM/xsKFyyGXyw26z127dsDH52O4uhZlGBMRmaBsAzkiIgJ37txB\nw4YNAQBTpkyBtbU1AMDZ2Rk3btzI1wGNRWjoRezatR1KpRKDB4/AqFGD8fPPxwEAEycGoF27jqhY\nsRJmz56G5ORkaLVaDB/+PcqXr5Cj/bds2fit/V2+fAkKRQoiIx/g0aOHGDp0FOrVa4CjR3/Gvn27\nIZFI4O/fFenp6bh58zpGjx6KsWMnYdq0idiwYRtCQy9i7dofYGFhATc3d4wbNxm///4r/vnnChIT\nExAZ+QBdunRHq1Zt823diIgoZ7IN5Hnz5mHSpEkIDg4GgIxXdlqtFkFBQRg0aBAAQK1WY9SoUXj0\n6BG++OIL9OrVK8/DTT07EYcignN9f6lUAp1OeO3PWpdri6n1Z+ZqfxERd7Bz5wFYWVllevuePTtR\np059tG7dFvfu3cWyZQuxdOkPuXqsl549e4qFC5fj3Lmz+Omn/ahRwxubN6/Hli07oVanY9asKZg7\ndzHWr1+NhQuX4/nzxIz7Llw4B0uWrEKxYsWxePE8/PbbUUgkEkRE3MHq1Rvx8GEUpkwZz0AmIsrE\n30/OI0mdiCZlviiQx8sykIODg+Ht7Q1PT8/X/lyr1SIgIAB169ZFvXr1AAABAQFo06YNJBIJunXr\nhtq1a6NatWpZPrizszzLPlC5rRWkUklOn0um3ry/3NYqy3LvlxwcbCCXv9rWyUmOypUrwcPDFQAg\nkUgybrO2toSTkxxhYTcQHx+PkyePAQDS0lLfeiyZTIpx40ZkvL/u7OyM5cuXZ7o/Oztr1KtXB25u\nDvDy+gBpaal4/vwZKlQoj1Kl3AAAGzasy9hv0aL2kMnSYWEhhaWlFhYWMlStqn+F3rDhp7hw4QIq\nV66Mjz+uheLFneDgYInUVEW265GT9aLscR0Ng+uYd1zDdxMEAccijmHW6Vk4HXkacks5UsalQCJ5\nO4sMvY5ZBnJISAiioqIQEhKC6OhoWFlZoXjx4ggODkaZMmUwePDgjG07d+6c8XXdunURHh6ebSBn\nd6WMgJqTEVBzck6eR6bc3BwyvaJUTq4ylZysglKpztg2MVEJQZBkfC8IQsbXCkVqxu1DhoxC1arV\n3/lYWq0Oc+Ysee095JiY5Ez3p1CkwdLSFjExyUhIUECt1uD5cxVUKnWm+42NTcHz5wpoNDrExSmg\n0WgztouLS4JKpUFysgpqtQ4xMclQKpXQanVZrse71pDeD9fRMLiOecc1zJxO0OHI3cNYFroIV2Mu\nAwCalG6G7z8eh9jYlLe2z+065vpqT0uXLsX+/fuxZ88edOjQAQMHDkRsbCwsLS0xdOjQjO3u3r2L\nUaNGQRAEaDQahIaGokKFnL13aqokEglUKhVUKhXCw8MAAJUrV8WpUyEAgHv37mLXru152l9mypQp\ni8jIB1AqlUhLS8Pw4QMhCAIkEim0Wm3GdkWKFIFEIkF0dDQA4MqVUFSsWCkXz5SIqPDS6DTYE7YT\nn+2qg29/7YZ/Yq6gTbmvcbzDaQS12oeaxWoV2CzvfT3koKAgpKWloXv37gCAcuXKYerUqShevDj8\n/PwglUrh6+uL6tWrZ7Mn09a2rR/69fsGZct+CC8vfdD5+XXCrFlTMXBgH+h0OgwfPjpP+8uMra0t\nevfuj+HDBwIAOnXqAolEgpo1fTBwYG9MmDA1Y9uAgImYNm0CZDIZPDxKoXHjZjh27JfcPWEiokJE\npVFhd1gQVlxeisik+5BJZOjk1QVDfUaigvNHoswkEQRByH6z/JHfh014aCbvuIaGwXU0DK5j3pn7\nGirSFdh6YxN+uLIcT5XRsJZZo0ul7hjkPQyli5TJ8X7y45D1e79CJiIiMjXP0xKx/toarPsnEPGq\neNhZ2mOQ9zD0rzEIxeyKiz0eAAYyEREVYjHKGKy5ugobr69DSnoynKydMLr2WPSt3h/ONi5ij/ca\nBjIRERU6j5IfYtWVZdh+cwtUWhXcbN0xsnYAelb5FvZWxnnaFwOZiIgKjbuJd7A8dAn2hu9Cui4d\npew9MdhnODpX7AZbC1uxx8sSA5mIiEzezbgbWHZpIX6K+BE6QYdyTuUxzGcU2lfoCEuZpdjj5QgD\nmYiITNalpxew9NJC/Hpff0pn1aLVMdxnFFp+2AYyqWldcZCB/IYnTx6jRw9/eHlVBKDv6O7a9Rt8\n/nmj997X/v27kZiYiM8+a4hTp0LQu/d3mW738tKJlpbZ/y3u7t07WLx4/luXbPz88zqoVq1Gxveu\nrq6YNm3Oe8/8pqNHj6JWrQa4fTssy+dARFRQBEHAmUensDR0EU4/DAEAfFy8DkbUGo3GpZtlWnNp\nChjImShdukxG4CUlPUevXl1Rt249WFvb5Gp/FSp4oUIFr3fe/vLSiTkJ5Hext7c3yHWV37R27Vqs\nWdMg2+dARJTfBEHAbw+OYsmlhbj09AIA4PNSjTC81mjUL/mJyQbxSwzkbBQp4ghX16KIi4vDpk3r\nYGFhiaSkREyfPhfz58/C48ePoNFo0KdPf9Sq9TEuXvwby5cvgouLK1xdi6JkSQ+Ehl7EgQN7MHPm\n/CwvnbhsWSAOHvwRv/9+FBKJFJ9+2hCdO3fDs2dPMWnSWFhaWqJ8+Zw3yDx58hgTJ47Bhg3661T3\n7t0dM2fOw8aNa1G0qBvCwv7F06fRmDx5Jry8KmLHji0ICTkOiUSK/v0H49atmwgLC8P48d/Dz69T\nxnM4fvw37N69AzKZDF5elTB8+Ghs2LAm00tFEhHllVanxaGIYCwNXYSbcdcBAM0/aInhPqPgU6y2\nyNMZjlEHst3UibA+lPvLL0Iqgcsbl19Ma90Wiqk5v/zikyePkZT0HO7uxQDoO6LHjJmAo0d/hqtr\nUYwbNxmJiYkYNqw/tmzZhTVrVmLSpBmoUOEjjB49FCVLemTsS6lUZHnpxJiYZwgJOY4fftgAABgw\noDcaNWqCAwd2o3HjZujYsTO2b9+MO3fCc78mL6jVaixevBLBwftw9OjPkMvlCAk5jjVrNuPx40fY\nvn0zxo6dhKCgrZg9ewFCQy++eA5KrF27Cps2BUEulyMgYETGbW9eKpKBTER5odaqsS98N5aHLsbd\n5xGQSqRoV6EDhvmMQiXXymKPZ3BGHchiiYx8gMGD+wEArKysMHHiNFhY6JeqcuUqAIDr1//B1auX\n8c8/VwAAaWlpSE9Px5MnT1Chgv5VrLe3D9LS0jL2e//+PZQuXRbW1jawtrbB3LmLX3vcf/+9gYcP\nozBkiP59WqVSgejox7h//x4aNWoCAKhZszbOnTv71swpKSkZMwNAuXLl4e/f7Z3PsUaNmgAAN7di\nuHnzBsLDw1C5clVIpVKUKuWJsWMnZXq/qKhIlCpVOuNqVTVr1kJ4+C0AQPXq3gAAd3d3pKS8fXUU\nIqKcSNWkIujfrVh5eRkepTyEpdQS3Sv3xKCaw/ChYzmxx8s3Rh3Iiqkz3+vV7Jvc3BwQn4uu0f++\nh/wmCwvLjH/36PEtmjZt/trtUumrC2i9WRMulcogCLp3Pq6FhSXq1WuAgIAJr/35jh1bIJFIX+wz\n8/tn9h5ydPST177XaDQZX7+8HvPLOWUyKXS67GvNJZLXn5dGkw5ra+tM90lE9D6S1UnYdH0DVl9d\nidjUGNha2KJf9QEY6D0UJe09st+Bicvy8ov0bpUrV8WZM38AABIS4rFmzSoAQNGiboiMvA9BEHD5\n8qXX7pPdpRO9vCohNPQSVCoVBEHA0qULkZamQunSZXDr1k0AyDg8nBNyuR0SEuIhCALi4mLx+PHD\nd27r5VUJ165dhUajQXx8HMaN01+p6s1g9fQsg4cPI6FUKgAAly+Hwsur8B06IqKCE6+Kw7y/Z8Fn\nW1XMPDcFado0DPcZjUvdb2DmJ/PMIowBI3+FbMx8fZsgNPQC+vf/FlqtFt9+qz9c3K/fQEycOAbF\ni5fIeN/5pewunbhixVp07NgZgwb1hVQqxWefNYS1tQ06dOiMSZPG4tSpkyhXLufXmS5SpAhq1/4f\n+vTpgfLlK2T5KekSJUriiy++xODB/SAIAr77bhAAoFKlSujbtwcGDBia8RwGDRqGUaOGQCKRonp1\nb9So4Y2LF8+/1/oREUUrniDwykpsubERSo0CrjauGF9nMr6t2hdFrB3FHq/A8fKLlCWuoWFwHQ2D\n65h3xrCGD5LuY+XlZdj57zaodWqUsCuJgd5D0K1yT9hZ2ok6W07x8otERGSywuPDsPzyYuwP3wOt\noEWZImUx1GckOnp1hrXMWuzxRMdAJiKifCEIAm7G3UBI1AmciPodZx7+AQECKrpUwjCfUfiqfDtY\nSBlDL3EliIjIYJ4pn+HUw5M4GXkcfzw8iWfKpxm31Sr2MYbUHIHmH3wJqYSfKX4TA5mIiHItTZuG\nv5+cw8mo4wiJOoHrsf9k3OZm644OH/mjoacvPvf0hbvcXcRJjR8DmYiIckwQBIQnhCHkRQCffXwG\nqZpUAIC1zBqflWqEhp6+aOjpiyquVU2+X7ogMZCJiChL8ao4nIoKQUjUCYREncBjxaOM2yq6VMLn\nnr5o5OmLuiUaQG4pF3FS08ZAJiKi16i1alx6eiHjVfCVZ5chQH+GrIuNC74u3x4NPRvjc89GZlPa\nURAYyEREZk4QBNx7HoGTUSfwR9QJnH50Cop0fR+9hdQC9Uo2QENPXzTybIxqbjX4gax8wkAmIjJD\nz9MScfrhqReHoY8jMvlBxm3lnMq/eB+4MRqU/AT2Vu8usyDDYSATEZkBjU6Dy88u4cKNP3H41hGE\nPrsI3YuL1RSxckSrD7/K+DBW6SJlRJ7WPDGQiYgKqcikBwiJOoGTUcdx+uEfSFI/BwBIJVLUKvZx\nRgDXdK/Fgg4jwP8CRESFRIo6GX8+PoOTkb8jJOoE7j6PyLittEMZtC3fHl9VbYnqDh/D0dpJxEkp\nMwxkIiITpdVpcS32Kk5GHkfIwxO4EH0eGp3+uud2lvZoXvZL/SlJpRvjgyIfQiKRGMXFJShzDGQi\nIhOSpk3Dz3cP4ui9n3HqYQjiVfEAAAkk8Hav+eLT0E1Qq9jHsJRZijwtvQ8GMhGRCYhMeoCtNzYh\n6NZWxKbGAgBK2nmgS8XuaOjpi888G8LFxlXkKSkvGMhEREZKq9PiRORv2HR9PY5H/gYBApytnTGg\nxhD4V+yKii6VWE1ZiDCQiYiMTIwyBkH/bsXWm5sQlRwJQH+lpJ5VeqNN+a9ha2Er8oSUHxjIRERG\nQBAEnI8+h83X1+FQxE9I16VDbiFH98o90bNKb1RzqyH2iJTPGMhERCJKVidhb/hubLm+Af/G3wQA\nfOTshZ5VeqOjV2cUsXYUeUIqKAxkIiIR3Ii9js03NmBf+G4o0lNgIbXAV+XaoWfV3qhf8hO+N2yG\nGMhERAUkTZuGQxHB2Hx9A/6OPgcA8LAvhSE1h6Nr5W9QTF5M5AlJTAxkIqJ89iDpPrbe2ISdt7Zl\nnLLUyLMxelXtiyZlmrG2kgAwkImI8oVWp8XxyGPYfH3Da6csDfQeih5VeuFDx3Jij0hGhoFMRGRA\n7zplqVfVPmhT7mvYWNiIPCEZKwYyEVEeCYKA80/+wuYb63nKEuUaA5mIKJfedcpSr6p90OEjf56y\nRO+FgUxE9J7edcpSr6p9UK9kA56yRLnCQCYiyoF3nbI0tOYIdKncg6csUZ4xkImIsvDylKWgf7ci\nThUHAPAt3QQ9q/ThKUtkUPxJIiJ6Q2anLLnYuGCQ9zD0qNILHzh+KPaIVAgxkImIXsjslKXaxf6H\nnlV785QlyncMZCIyay9PWdp0fR0O3z344pQlO3Sv3As9q/ZGtaLVxR6RzAQDmYjMVlLac3Q90hHn\nn/wFAPByroieVXvzlCUSBQOZiMySSqPCN790wfknf6Fx6aYY6jMSdUvU5ylLJBoGMhGZHa1Oi0HH\n++HPx6fR8sM2WN9sC2RSmdhjkZmTij0AEVFBEgQB406PxqGIYNQv+QkCm6xnGJNRYCATkVlZdHEe\nNt/YgCqu1bC1xU5+cpqMBgOZiMzGlhsbMf/CbJR2KINdrfbzg1tkVBjIRGQWDkccxJhTI1HUtij2\ntP4RxeyKiz0S0WsYyERU6P356DT6//YtbC3k2NlyPz50Ki/2SGQCZNevwfL0HwX2ePyUNREVatdj\nr6HHL50hQMCm5ttRw72m2CORkZOFh8Fu3ixYHwqGIJcj9t4ToABOh8vRK2SVSoUmTZrgwIEDePLk\nCXr27Ilu3bqhZ8+eiImJAQAcPHgQ7du3R4cOHbB37958HZqIKCfuP78H/8PtkKJOxsrGa9DQ01fs\nkciISR/ch8OQ/nD+rA6sDwUj3acWnu/cXyBhDOQwkAMDA+HoqP/ww9KlS9GxY0ds374dTZs2xaZN\nm6BUKrFq1Sps3rwZ27Ztw5YtW5CYmJivgxMRZSVGGYNOh7/GM+VTzPpkHr6u4Cf2SGSkpE+jYT9m\nJFzq14LN7iBovSri+ZadSPzlBNLrNSiwObI9ZB0REYE7d+6gYcOGAIApU6bA2toaAODs7IwbN27g\n6tWrqFatGhwcHAAAPj4+CA0Nha8v/zZKRAUvRZ2MLj/74d7zuxjuMxp9qvcXeyQyQpL4OMhXLIXt\nxrWQpKZC88GHUAaMR1rb9oCs4M9Nz/YV8rx58zB27NiM7+VyOWQyGbRaLYKCgtC6dWvExsbCxcUl\nYxsXF5eMQ9lERAUpTZuGnke74WrMZXSt1APj6kwSeyQyMpLkJMgXzIFL7eqQr1oGnbMLkhctR8KZ\nC0hr31GUMAayeYUcHBwMb29veHp6vvbnWq0WAQEBqFu3LurVq4dDhw69drsgCDl6cGdnOSws8veJ\nu7k55Ov+zQHX0DC4joaR1TrqBB267O+LUw9Poo1XG2z22wALKT+7+iaz/VlMTQVWrQLmzgXi4gA3\nN2DGdMj694eDjQ3ed1UMvY5Z/qSGhIQgKioKISEhiI6OhpWVFYoXL47g4GCUKVMGgwcPBgC4u7sj\nNjY2437Pnj2Dt7d3tg+ekKDM4/hZc3NzQExMcr4+RmHHNTQMrqNhZLWOgiBgwpkA7L6xG3VK1MOK\nz9chIS61gCc0fmb5s6hWw2bHVsiXLIAs+gl0RRyROm4SlH0HAPb2QHK6/p/3kNt1zCrEswzkpUuX\nZny9YsUKeHh4IDY2FpaWlhg6dGjGbTVq1MDEiRORlJQEmUyG0NBQjB8//r0HJSLKrWWhi7D+2hpU\ncqmMbS12wdbCVuyRSGxaLaz374Hd/DmQRd6HIJdDOWwUlAOHQHB2yf7+Bey9j+UEBQUhLS0N3bt3\nBwCUK1cOU6dOxahRo9C7d29IJBIMGjQo4wNeRET5bfvNLZh9fjpK2XtiV6sDcLJxFnskEpMgwOrn\nQ7CbNxMWYbcgWFlB2ec7KIeNhlCsmNjTvZNEyOkbvvkgvw+bmOWhGQPjGhoG19EwMlvHX+79jF5H\nu8LJ2gmHvj6GCs4fiTSdaSjUP4uCAMuTx2E3ZwYsr16GIJVC5d8VylFjoPMsbdCHKvBD1kRExuzc\n47P47lgv2MhsENRyH8PYjFmc+wt2c6bD6q8/AQCqtu2gDJgAbfkKIk+WcwxkIjJJN+NuoPsv/tAI\nGmxvsRs+xWqLPRKJwOKfK5DPmQHr478BANKaNYdizERoq1UXebL3x0AmIpMTlRwJ/8Pt8DwtET80\nWQff0k3FHokK2H/7pgFA3eBTKMZPhubjOiJPlnsMZCIyKXGpceh4qC2iFU8wvcFs+H3USeyRqABJ\nH9yH3cK5sN67CxKdDuk1faAYPwXpnzUssM7p/MJAJiKTkaJOQdef/RCReAeDaw5H/xqDxR6JCoj0\naTTki+fDZvsWSNLToalUGYqxk6Bu/qXJB/FLDGQiMglqrRrd93RF6LNL6OTVBZPqThN7JCoAb/ZN\na8t+AMWYCaL1TecnBjIRGT2doMOwEwPxa8SvaFrmCyxuuAKSQvKqiDInSU6C7ZofYBu4EtLkJGhL\nlIRyxlyoOncDLC3FHi9fMJCJyKgJgoApZydg/+09qFuqLtY12wJLWeH8hUwAUlNhu2k95MsXQRof\nD52rK1Kmz0Zqzz6AjY3Y0+UrBjIRGbWVV5ZhzdVV+MjZC4c7H4ZOYSX2SJQf1GrYBG2DfPH8jL5p\nxdiJSO03AIK9eTQ/MpCJyGjturUDM/6ajJJ2Htjd6ke4yl0RoyikLVPm6s2+aVtbKIeOhHLQUKPs\nm85PDGQiMkrH7v+CEScHw8naCbtb/wgPh1Jij0SG9GbftKWlSfRN5ycGMhEZnb+fnEffYz1hJbPC\njpZ74eVSUeyRyFBe9k3PnQHLK/q+6dQu3fOlb9rUMJCJyKiExd9CtyMdoNaqsbXFTnxc3HSbl+h1\nb/VNf9UOyoDx0FZgBznAQCYiI/Io+SE6HfoaiWmJWO4biKZlm4s9EhnAW33TTb+AYuwkk+ybzk8M\nZCIyCvGqOHQ6/DUeKx5hUr3p8K/YVeyRKI/e6puu/wkU46dA8z8e9cgMA5mIRKdIV6Drzx0RnhCG\n/jUGY7D3MLFHojyQRj7Q903v2fmqb3rcZKR/3qjQ1FzmBwYyEYkqXZuOvr9+g0tPL6B9hY6YWn8m\nW7hMlPRpNORLFsBm22Z933TFSvq+6RYtGcQ5wEAmItEIgoARIYPxe+QxNPJsjGW+P0AqkYo9Fr0n\nSXwc5CuXwXbDmld90wHjkfa1X6Hrm85PDGQiEs2Mc1OwJ2wnfNxrYUPzbbCSsYXLlEhSkmG7epVZ\n9U3nJwYyEYki8MpKrLy8FOWdKmBHy32wt7QXeyTKqZd90ysWQxoXZ1Z90/mJgUxEBW5v2C5MOTse\nxe1KYHfrH+Fq6yr2SJQT6en6vulF8/R90w5FzK5vOj8xkImoQJ2I/A3DTg6Eo7UTdrf6EZ4O5t3O\nZBJe9k0vmAPZA/Pum85PDGQiKjCXnl7At0e7w0JigW0tdqGSa2WxR6KsCAKsjhyG3dwZGX3Tqb37\nQTl8NHTFios9XaHDQCaiAnE7IRxdf+4AlVaFzc2DULdkfbFHoncRBFiGnIDdnOmv+qY7d9P3TZcu\nI/Z0hRYDmYjy3eOUR+h06GvEq+KxpOFKNP/gS7FHonewOH9O3zd99gwA9k0XJAYyEeWrRFUC/A+3\nw8OUKIyvMxldK/cQeyTKhMW1q/q+6d+PAdD3TSvHToSmWg2RJzMfDGQiyjepmlR0O9IJt+L/RZ9q\n32GYzyixR6I3yG6HQz5vFmwO/giAfdNiYiATUb7Q6DTod6wn/o4+h7bl22HmJ/NYiWlE2DdtfBjI\nRGRwgiBgdMgw/Hr/F3xWqhFWNF7DSkxjER0N+4lTYLN1E/umjQwDmYgMbs75GQi6tQ013Gpic/Pt\nsJZZiz2S2ZMkxEO+chmwfjVsU1OhLVMWijET2DdtRBjIRGRQ6/4JxNLQhfjA8UMEtdwHeys2OIlJ\nkpIM2zU/wPaHFZAmJwEeHkgeEcC+aSPEQCaiHBMEAWnaNKi1aVC9+HeaVoU0rRppGhUux4Riwpkx\ncJcXw57WwXCTu4k9svlKTYXt5g2QL1/0Wt+0/ejhUKVoxJ6OMsFAJjIBOkEHtVb9Kvy0Kn0oal6G\n4st//nu7GqoX26Vp0l58nZN9vAzcN7bXqKDWqbOd1cGqCHa1OoAyRcrm/8LQ2172TS+eD9mTx2/1\nTdvb2gIpyWJPSZlgIBMZoeux1zD4+HeITHoAtTYtR0FoCFKJFDYyG1jJrGAts4G1zBrO1i6wklnD\nxsIaVjJrWGf8Y/PqawtrWEn127Qp1w5VilYtkHnpP7RaWP+4D3bzZ0N2/56+b3rICCgHD2PftIlg\nIBMZmVMPQ9Dzl65ISU9GZdeqsLWwgfWLkNSHpXWmQWiVEZJWb23/3zDNdB8v/txCyl8JJudl3/S8\nmbC49S/7pk0Y/+8jMiL7w/dg6IkBkECCNU034usKfmKPRMZKEGD5x0l93/TlUPZNFwIMZCIjIAgC\nVl1Zjul/TUIRK0dsaRGEBh6fij0WGSmLv8/r+6b/PA2AfdOFBQOZSGRanRaT/hyL9dfWoIRdSexs\ntR+VXauIPRYZIdm1f2A3dwasf/sVAPumCxsGMpGIVBoVBv7eF4fv/oSKLpWws+V+eDiUEnssMjKy\nO7f1fdM/HQDwom963GRo6tQVeTIyJAYykUgSVPH45pcuOPfkLOqX/ARbWgTB0dpJ7LHIiEijIiFf\nOBc2u4P0fdPeNaEYP4V904UUA5lIBA+To+B/uB3CE8LwVbl2WNlkDeslKYPk6VPYLV3Avmkzw0Am\nKmDXY6+hy89+iFY8Qf8agzG1/kxeeIEAvOqbtl2/GpKXfdMB45HWrgP7ps0AA5moAP33HOPpDWaj\nf43BYo9ERkCSkgzbtYGwXbVOZRLKAAAgAElEQVQc0uQkaEuUhHL6HKi6dGfftBlhIBMVkH3huzHs\nxEBIIMHappvQtkJ7sUcisalUsN28HvJl/+mbnjYbqT17A7a2Yk9HBYyBTJTPBEHA/D/nY8zvY3iO\nMemlp8Nm53bIF8171Tc9ZgJSvxsIwZ5XxzJXDGSifPTmOca7Wh1AJdfKYo9FYnlX3/SgoRBcXMWe\njkTGQCbKJ6maVAz8vS9+vnsQVd2rYnvzvShp7yH2WCQGQYDVLz/r+6b/vcm+acoUA5koHySo4tHj\nl844/+QvNCj5KQ53P4j0ZH5K1uxk0jet8u8Kxeix7JumtzCQiQwsKjkSnQ+3R3hCGNqWb4cVjdfA\nycYJMcm8Bq05eatvus3XUI6ZwL5peicGMpEBXY+9hs6H2+OpMhoDagzBlPozeI6xmXmrb7pJMyjH\nTWLfNGWLgUxkIC/PMVakp2BGgzn4rsYgsUeiAvRW33S9BlCMn8K+acoxBjKRAbx2jnGzTfiqfDux\nR6ICkmnf9LjJSG/oy5pLei8MZKI8EAQBK68sw4y/JqOIlSO2ttiJ+h6fiD0WFQDJ06eQL1sI2y0b\n9X3TXhX1fdNftmIQU64wkIly6b/nGJe088DOVvt5jrEZkCTEQ75qub5vWqlk3zQZDAOZKBf+e45x\nJZfK2NlqP88xLuTe6psuXgLKqbP0fdNWVmKPR4UAA5noPSWo4tH9iD/+jj6HBiU/xeYWO3gd48Ls\nzb5pFxekTJ2F1F592DdNBpWj8zFUKhWaNGmCAwf0nx7cunUrqlSpAoVCkbFNlSpV0L1794x/tFpt\n/kxMJKKo5Ei0OtAMf0efw9fl22NX6wMM48IqPR02WzfBpW5N2E8eD6jToQgYj/gL/yB14BCGMRlc\njl4hBwYGwtHREQAQHByMuLg4uLu7v7aNvb09tm3bZvgJiYzEtdh/0OWwH54qozHQeygm15vOc4wL\nI51O3zc9b9arvunBw6EcPIx905Svsg3kiIgI3LlzBw0bNgQANGnSBPb29jh06FB+z0ZkNP6IOole\nR7tBkZ6CmQ3mol+NgWKPRIYmCLA6egR2c2e86pv+ti+UI75n3zQViGz/ej9v3jyMHTs243t7e/tM\nt1Or1Rg1ahT8/f2xadMmw01IJLK9YbvQ+ef2UGvTsK7ZZoZxYSMIsAw5AacWvnD8pjNkYbeg8u+K\n+L9CkTJ3EcOYCkyWr5CDg4Ph7e0NT0/PbHcUEBCANm3aQCKRoFu3bqhduzaqVauW5X2cneWwsMjf\n0wTc3Hht0bwy1zV8eR3jscfHwsnGCcGdgvF52c9zvT9zXUdDM+g6nj0LTJgAhITov/fzg2T6dNhU\nqgQbwz2K0eHPomEYeh2zDOSQkBBERUUhJCQE0dHRsLKyQvHixVG/fv23tu3cuXPG13Xr1kV4eHi2\ngZyQoMzl2Dnj5uaAmBgW+ueFua6hVqfFxD/HYMO1tShp54FdrQ+gol2lXK+Fua6joRlqHd/qm27c\nVN83Xd1bv0Eh/m/Fn0XDyO06ZhXiWQby0qVLM75esWIFPDw8Mg3ju3fvYtWqVVi4cCG0Wi1CQ0PR\nvHnz9x6UyBikalIx4Lc+OHLvECq5VMHOVvt4jnEhIbtzG/L5s2AT/KJvum59fd903XoiT0aUi/OQ\nAwMDcfbsWcTExKBv377w9vZGQEAAihcvDj8/P0ilUvj6+qJ69er5MS9RvvrvOcafeHyGzc13oIi1\no9hjUR5JoyIhXzQPNrt26Puma9SEYtwkpDdqzJpLMhoSQRAEsR48vw+b8NBM3pnTGkYlR8L/UDvc\nTgxHuwp+WOYbCGuZtUH2bU7rmJ/edx0z+qa3boJErdb3TY+ZCHXL1mYbxPxZNIwCP2RNZC6uxf6D\nzofb45nyKQZ5D8OketN4jrEJe6tvunRZKALGIa19R/ZNk9FiIJPZC4k6gW+Pduc5xoVARt/0Dysg\nTXrOvmkyKQxkMmt7wnZi+MlBkElkWP/FFrQu11bskSg3VCrYbtmg75uOjWXfNJkkBjKZJUEQsOLy\nEsw8NxWO1k7Y2mIn6pVsIPZY9L7S02Gzawfki+ZB9vgRdPYOUASMR+p3AyE4FBF7OqL3wkAms6PV\naTHhTAA2Xl8HD/tS2NlqPyq6VBJ7LHof7JumQoiBTGblzXOMd7XajxL2JcUei3JKEGD1y8+wmzsT\nFv/e0PdN9+qj75suXkLs6YjyhIFMZiNeFYfuR/xxIfo8zzE2NYIAy1MhwIJZcPz7bwhSKVSdukAx\neix0ZcqKPR2RQTCQySxEJj2A/+F2uJN42+DnGFP+srhwHnZzZsDqzCkAQFrrtlCMmQDtR14iT0Zk\nWAxkKtTUWjV2hwVh7vmZiEl9xnOMTYjs+jV93/SxowD0fdPW8+ciybOCyJMR5Q8GMhVKKo0KQbe2\nYUXoEjxKeQhrmTVmfzIffar3F3s0yoYs4jbk8zLvm3ZzcyjUF34g88ZApkJFma7E9pubsfLKMkQr\nnsDWwhbfVR+IQTWHobgdP/RjzDL6pncHQaLVsm+azA4DmQqFlPQUbLm+EauuLENsagzkFnYYXHM4\n+tcYDHe5u9jjURYkz57p+6a3bGTfNJk1BjKZtGR1EjZeW4fAqysQr4qHvaUDRtQajX7VB8HVluej\nGjNJYoK+b3pdIPumicBAJhOVqErAumurse6fQCSmJcLR2gnffzwOfav1h5ONs9jjUVZSUiBfFwjb\nVcv1fdPFirNvmggMZDIx8ao4rLm6CuuvrUWyOgkuNi4YX2cyelfrBwcrViUatcz6pqfMROq3fdk3\nTQQGMpmIGGUMAq+uwMZr66DUKFDU1g0j6s1Az6q9YW9pL/Z4lBX2TRPlCAOZjNpTRTRWXlmGrTc2\nIlWTimLy4hhXZyK6V+4FuaVc7PEoKzodrIP3Qz5vFizu3YVgYwPloGFQDhnOvmmiTDCQySg9Sn6I\nFZeXYMe/W5GmTYOHfSkMrjkcXSv1gI2FjdjjUVYEAVa//gK7OTPYN030HhjIZFQikx5gWehi7Lq1\nHem6dJQuUhbDfEaik1cXWMn4gR9jZ3kqBHazp8Ey9BL7poneEwOZjMLd5xFYdmkR9obvgkanwQeO\nH2JEre/RvkJHWMosxR6PsmFx8W993/TpPwCwb5ooNxjIJKrbCeFYcmkBDtzeC52gw0fOXhheazTa\nlm8PCyl/PI2d7MZ1fd/0r78A0PdNK8dNgqa6t8iTEZke/sYjUfwbdxNLLs3HT3d+hAABlVyqYGTt\n79Hqw68gk7IUwtjJIm5DPn82bH7cD+D1vmkiyh0GMhWoazFXsejifBy5dwgAUK1oDYysHYAWH7Tk\nFZhMgPRhlL5vetcO9k0TGRgDmQpE6NOLWHxxPo490F9Kz8e9FkbVHoMmZb6AhL/Ijd5bfdMfeUEx\ndhL7pokMiIFM+er8k3NYfHEeTkYdBwD8r3hdjKo9Bg09fRnEJiDTvunvxyLNrxP7pokMjIFMBicI\nAs4+PoPFF+fj9CP9p24/8fgMI2sHoEHJTxnEpiAlBfL1q2G7ctmrvukpM6Hq2oN900T5hIFMBiMI\nAv54eBKLL87HuSdnAQANPX0xsvYY1C3BD/uYBJUKtls3Qr50EaSxMeybJipADGTKM0EQcDzyGBZd\nnIdLTy8CAJqW+QIjawegVrGPRZ6OckSj0fdNL5z7qm/6+3FI7T+IfdNEBYSBTLkmCAKO3j+CxRfn\n42rMZQBAiw9aYWSt71HDvabI01GOvOybnj8bFncj2DdNJCIGMr03naDD4YifsPjSAtyMuw4JJGhT\n7muMqPU9qhStKvZ4lBMv+6bnzoTFzesQLCzYN00kMgYyvZe/n5zHqJAhCEu4BalEinYVOmBEre/h\n5VJR7NEohyxP/6Hvm750Ud833bGzvm+67Adij0Zk1hjIlCNanRYrLi/BvL9nQYCATl5dMLzWKJRz\nqiD2aJRDb/VNt/pK3zftxb9MERkDBjJlK1rxBIN+74fTj/5ACbuSCGyyHvU9PhF7LMqhN/um1b5N\noBg3CZoafJ+fyJgwkClLR24fQY8DPRCnisMXZVtgaaMf4GrLD/uYgpd909bBByARBKTXqQfFhClI\nr1tf7NGIKBMMZMqUWqvGzHNTsfrqSlhJrTDrk3noU60/Sz1MgPTRQ33f9M7t+r7p6t5QjJ+E9EZN\nWHNJZMQYyPSWu88j0P/Yt7gScxkVXCpgdeONqOZWQ+yxKBuSZ88gX74Itps3vOqbHjMR6lZtGMRE\nJoCBTK/ZF74b3/8xAor0FHTy6oL17dYg9bkg9liUBUliAmx/WAH52h9e9E2XgeL7ceybJjIxDGQC\nAKSkp2DcqdHYHRYEO0t7rGq8Fh28/GFvZY9UJIs9HmXmZd/0quWQPk9k3zSRiWMgE67F/oN+x3oi\nIvEOarjVxJqmG/ChU3mxx6J3ebNv2tkZKZNn6Pum5XKxpyOiXGIgmzFBELDh2hpMPTsRap0a/WsM\nxsS6U2El46sro6TRwGZ3kL5v+tFDfd/06LFIHTCYfdNEhQAD2UzFq+Iw/MQgHL1/BK42rljReDWa\nlPlC7LEoMzodrH86APm8Wa/6pgcOhXLICAiuPAWNqLBgIJuhs4/OYMDvffBE8RifeHyGH5qsQ3E7\n9hcbHUGA1bGjsJsz41XfdM/eUI4MYN80USHEQDYjWp0Wiy7Ow+JL8yGBBOP+NwlDfUZCJuUncY2N\nvm96OiwvXYAgkbBvmsgMMJDNxOOURxjwex/89fhPlLL3xOqmG/G/EnXEHoveYHHpAuxmz4DV6RAA\nQFrLNvq+6YqVxB2MiPIdA9kMHL13BMNODEBCWgJaffgVFjdcDicbZ7HHov+Q3bgOu3kzYX30CABA\n3aixvm/a20fkyYiooDCQCzGVRoXpf03C+mtrYCOzwfzPluCbKt+y/tKIyO7e0fdN/7j/Vd/0+MlI\nr9dA7NGIqIAxkAupOwm30fdYT9yIu4aPnL2wttlmVHatIvZY9MJbfdPVakAxYTL7ponMGAO5kBEE\nAbvDgjD21CgoNUp0r9wTMxrMhdyShRHGQBITA/myha/6pit8BMXYiVC3bANIpWKPR0QiYiAXIsnq\nJHz/xwgcuL0XDlZFsK7ZZnxVvp3YYxEAJCRAPns25GsDIVEq9H3To8cirYM/+6aJCAADudC48iwU\n/Y71wv2ke6hVrDZWN92IMkXKij0WKRSwXb8aWLUMdomJ0LoXg3LydKi6fcO+aSJ6DQPZxOkEHVZf\nXYVZ56ZCo9NgaM2RGPO/CbCUWYo9mnlLS9P3TS9ZCGlsDODiwr5pIsoSA9mExShjMPREfxyP/A1u\ntu5Y1WQtGnr6ij2WeXuzb9rOHopRY2A3aRxS1XyPmIjejYFsok49DMHA3/vimfIpGnk2xorGa+Au\ndxd7LPP1sm96/mxYRNx5q2/aztEBiOFlLIno3RjIJiZdm44FF+ZgWegiyKQyTK43AwO9h0Aq4asv\nUWTWN/1NbyhHfg9diZJiT0dEJoSBbEIikx6g/2+9cfHp3yhTpCzWNN0In2K1xR7LbFmeOQW7WdNe\n9U138Ifi+3HsmyaiXGEgm4hDEcEYcXIIktTP8XX59ljw+VIUsXYUeyyzxL5pIsoPOTrOqVKp0KRJ\nExw4cAAAsHXrVlSpUgUKhSJjm4MHD6J9+/bo0KED9u7dmz/TmqFUTSpGhwxH7197QKNLx9JGq7C6\n6UaGsQhkN66jSA9/OLdoDKvTIVA3aoyEYyFI2rSdYUxEeZajV8iBgYFwdNQHQHBwMOLi4uDu/uoD\nREqlEqtWrcK+fftgaWkJPz8/NG3aFE5OTvkztZm4Ff8vvjvWC//G30Rl16pY23QTPnLxEnsss/NW\n3/T/6ur7put/IvZoRFSIZBvIERERuHPnDho2bAgAaNKkCezt7XHo0KGMba5evYpq1arBwcEBAODj\n44PQ0FD4+vIUnNwQBAHbbm7GpD/HIlWTim+r9sXU+rNgY2Ej9mhmJbO+aeX4SVD7NmXfNBEZXLaB\nPG/ePEyaNAnBwcEAAHt7+7e2iY2NhYuLS8b3Li4uiImJMeCY5uN5WiJGhQzDwYgf4WTthB+arEfL\nD1uLPZZZkcTEQL58EWw3rWffNBEVmCwDOTg4GN7e3vD09HyvnQqCkKPtnJ3lsLDI3x5fNzeHfN2/\nIZ17eA7++/zx4PkDfFL6E+xotwOlHUuLPZZJrWGeJCYCCxcCS5cCCgVQpgwwdSosunWDo0XeP/9o\nNuuYz7iOecc1NAxDr2OWv2VCQkIQFRWFkJAQREdHw8rKCsWLF0f9+vVf287d3R2xsbEZ3z979gze\n3t7ZPnhCgjKXY+eMm5sDYkygjEEn6LDy8lLMOT8DOkGHUbXHYFTtMbBQW4g+v6msYZ686JuWr1wG\n6fMXfdMTp+n7pq2tgYTUPD+EWaxjAeA65h3X0DByu45ZhXiWgbx06dKMr1esWAEPD4+3whgAatSo\ngYkTJyIpKQkymQyhoaEYP378ew9qjp4qn2LQ7/1w6uFJFLcrgcAm69HA41OxxzIPb/RN65yckDJp\nOlJ792PfNBEVuPc+DhcYGIizZ88iJiYGffv2hbe3NwICAjBq1Cj07t0bEokEgwYNyviAF2XuScpj\n7A3fhdVXVyE2NQbNyjTHMt9AuNq6ij1a4feyb3rRPMgeRmX0TacOGAyhCE8nIyJxSIScvuGbD/L7\nsImxHZpRpivxy73D2HVrB049DIEAATYyG0yqNw19qvWHxAg/uWtsa5gnb/ZNW1sjtVdfKIeOhFC0\naL4+dKFaRxFxHfOOa2gYBX7ImvJOEAScf/IXdocF4ac7PyIlXf8fsHax/6FTxS74qtzXcLJxFnnK\nQk4QYPXbUdjNZt80ERkvBnI+eZB0H3vCdmJP2E48SLoPAPCwL4W+1b9DR6/OKOdUQdwBzcRbfdN+\nnfR90x98KPZoRESvYSAbUIo6GYcifsLusCCcfXwGACC3kKPDR/7wr9gVDTw+5VWZCshbfdNfttb3\nTVeqLO5gRETvwEDOI52gw5lHp7Dr1g4cuXsISo3+VK4GJT9Fp4pd0OrDNrC34gfcCors5g3YzZ0J\n66M/AwDUDX2hGDcJmpq1RJ6MiChrDORciki8jd23dmJv+C48SnkIAChTpCw6eXVBR6/OKF2kjMgT\nmhfp3QjYzZ8N6x/3sW+aiEwSA/k9JKoSEHznAHaHBeHS0wsAAAerIuhW6Rt0rNgFdYrXNcpPShdm\n0kcPIV88HzZB2/R901Wr6/umGzdj3zQRmRQGcjY0Og1Coo5j962dOHr/Z6Rp0yCVSNHQ0xf+Fbui\nedmWkFuyRKKgZfRNb94ASVoaNOUr6PumW33FvmkiMkkM5He4GXcDu28FYf/tPXimfAoA+MjZCx29\nuqDDR51Qwp6ny4hB8jwRtj8sh3xNICRKBbSepaH4fhzS/DoBBuibJiISC3+D/UdsaiwOhO/B7rCd\nuBZ7FQDgZO2EXlX7wN+rK7zdfXhIWixv9E3r3NyRMmkqVN166vumiYhMnNkHslqrxm8PfsXusCD8\n/uBXaHQayCQyfFG2BTp6dUGzss1hLeMvfNGkpcFm2ybYLVkIacwzfd/0xGn6vmk7O7GnIyIyGLMM\nZEEQ8E/MFewK24Efb+9DvCoeAFDFtRr8K3ZBuwod4SZ3E3lKM6fRwGbPTsgXzn3VNz0yAKkDh7Bv\nmogKJbMK5KeKaOwN3409YUG4Ff8vAKCorRu+qzEInby6oGrRaiJPSNDpYH3wR8jnzcrom1b2H1wg\nfdNERGIq9IGcqknF0Xs/Y3dYEEKiTkAn6GAltULrcm3RyaszGnk2gaXMUuwx6WXf9JyZsLhxTd83\n3eNbfd90SQ+xpyMiyneFMpAFQcCF6L9x8Nxe7Lq+G0nq5wAAH/da6FixC74u3x7ONi4iT0kvWZ45\nBbvZ02F58W/2TROR2SpUgRyVHIm9YbuwJ2wn7j6PAACUsCuJnlV6o6NXZ3zk4iXyhPRfFqEX9X3T\np04CYN80EZm3QhPIR+8dwTe/dIYAAbYWtmhXoQP61+mLavYfQyaViT0e/cdbfdOfN4Ji/GT2TROR\nWSs0gVzSviRalfsKvp5N0KZ8WzhYFeGFuI3MW33TH9fR9003+FTs0YiIRFdoArm6mzc2fLFV7DEo\nE+ybJiLKXqEJZDI+mfVNK8dMQFrrtuybJiJ6AwOZDE7yPBG2gSsgX/2Dvm+6lKe+b7qDP/umiYje\ngb8dyXAUCthuWAP5yqWQJrJvmojofTCQKe/YN01ElGcMZMq9N/qmBbmdvm96wGAIjk5iT0dEZFIY\nyPT+dDpYHwqGfO7MV33T3w3S90278aIcRES5wUCmnBMEWP3+K+xmz9D3TctkSO3eC8pRAeybJiLK\nIwYy5Yjln6dhN2vaq77pdh2gCBgP3YflxB6NiKhQYCBT1v7+G47fj33VN92iFRRjJ7JvmojIwBjI\nlCnZvzdhN3cm8MthWOFF3/S4SdD41BZ7NCKiQomBTK+R3o2A3YI5sD6wFxJBAOrXR+L3E9g3TUSU\nzxjIBACQPn4E+aL5sNm5DRKNBpoq1aAYPwmOnf2QHpsi9nhERIUeA9nMSWJjIV+2CLab1+v7psuV\nh3LsxFd907z4AxFRgWAgm6mXfdO2awIhVaSwb5qISGT8zWtuFArYblgL+colGX3TyRMmQ9W9F/um\niYhExEA2F2lpsNm+GXaLF/ynb3oqUnt/x75pIiIjwEAu7DQaWO/dBbsFc/7TN/09UgcMYd80EZER\nYSAXVi/7pufNgsWd2+ybJiIycgzkwuZF37R8zkxYXv+HfdNERCaCgVyIWJ49o++bvnCefdNERCaG\ngVwIWFy+BLvZ02H1x4u+6eYt9X3TlauIPBkREeUUA9mEveybtv7lMABA/VkjKMZNhKbWxyJPRkRE\n74uBbIKk9+7q+6b374FEEJBe+39QjJ+M9E8+E3s0IiLKJQayCZE+eazvmw7a+lrftLrJF6y4JCIy\ncQxkEyCJjYV8+WLYblr3qm96zASktfla3zdNREQmj4FsxCRJz2H7wwrYrvlB3zftUQrK78dB1bEz\n+6aJiAoZ/lY3RkolbNevedU3XdSNfdNERIUcA9mYqNWw2bYZ8iULIHv2FDpH9k0TEZkLBrIx0Ghg\nvW+3vm86KpJ900REZoiBLCadDlaHf4LdvFmwuB3+om96IJRDR7FvmojIzDCQxSAIsDp+TN83fe3q\ni77pnlCODIDOo5TY0xERkQgYyAXM8uwZ2M2eDsu/z73om/aDMmA8tB+WF3s0IiISEQO5gFhcCdX3\nTYecAMC+aSIieh0DOZ/Jbv2r75s+cggA+6aJiChzDOR8wr5pIiJ6HwxkA8u0b3rcRKibNmffNBER\nvRMD2UAkcXGv+qZVKmg+LAfl2InsmyYiohxhIOeRJOk5bANXwnb1KvZNExFRruUoMVQqFVq1aoWB\nAweiXr16CAgIgFarhZubGxYsWAArKytUqVIFPj4+GffZvHkzZDJZvg0uOqUSthvW6vumExLYN01E\nRHmSo0AODAyEo6MjAGD58uXo0qULWrRogcWLF2Pfvn3o0qUL7O3tsW3btnwd1iiwb5qIiPJBtm9u\nRkRE4M6dO2jYsCEA4Pz582jcuDEAoFGjRvjrr7/ydUCjodHAetcOuNSvBYdxoyFNSYFixGjEX/wH\nqUNHMoyJiChPsg3kefPmYezYsRnfp6amwsrKCgDg6uqKmJgYAIBarcaoUaPg7++PTZs25dO4ItDp\nYHXwRzh/XhdFhg6A9Gk0lN8NRNyFf6AcN5kXfyAiIoPI8pB1cHAwvL294enpmentgiBkfB0QEIA2\nbdpAIpGgW7duqF27NqpVq5blgzs7y2Fhkb/vM7u5OeTujoIA/PILMHEicPkyIJMBfftCMmkS5J6e\nkBt2TKOW6zWk13AdDYPrmHdcQ8Mw9DpmGcghISGIiopCSEgIoqOjYWVlBblcDpVKBRsbGzx9+hTu\n7u4AgM6dO2fcr27duggPD882kBMSlAZ4Cu/m5uaAmJjk976f5V9/wm7WtIy+6bR2HaAMGPeqbzoX\n+zRVuV1Deh3X0TC4jnnHNTSM3K5jViGeZSAvXbo04+sVK1bAw8MDly9fxq+//oqvvvoKx44dw6ef\nfoq7d+9i1apVWLhwIbRaLUJDQ9G8efP3HlRs7JsmIiKxvPeJskOGDMGYMWOwe/dulCxZEm3btoWl\npSWKFy8OPz8/SKVS+Pr6onr16vkxb75g3zQREYlNIvz3jeAClt+HTbI7pCC9f0/fN71vN/um34GH\ntwyD62gYXMe84xoaRoEfsi6spE8eQ754AWx2bGHfNBERGQWzCmT2TRMRkbEyi0Bm3zQRERm7wp1G\nSiVsVyxl3zQRERm9whnIL/qmsWwh7KOj2TdNRERGr3AFskYD6327YbdwLmSRDwA7OyhGjEbqwKGs\nuCQiIqNWaAJZdjscRXp2gcXtcAjW1lB+NxDy6VOglNiKPRoREVG2Ck0gW9y4Btm9u0jt3hPKkQHQ\neZSC3M3BrGouiYjIdBWaQE5r2x5prdvqLwJBRERkYgrXybcMYyIiMlGFK5CJiIhMFAOZiIjICDCQ\niYiIjAADmYiIyAgwkImIiIwAA5mIiMgIMJCJiIiMAAOZiIjICDCQiYiIjAADmYiIyAgwkImIiIyA\nRBAEQewhiIiIzB1fIRMRERkBBjIREZERYCATEREZAQYyERGREWAgExERGQEGMhERkRGwEHuAvJo/\nfz4uXboEjUaD7777Ds2aNQMAnD59Gn369EFYWBgA4NatWxg/fjwAoHHjxhg0aJBoMxujnK7jkiVL\ncP78eQiCgCZNmqBv375ijm1U3lzDEydO4MaNG3BycgIA9O7dGw0bNsTBgwexZcsWSKVSdOzYER06\ndBB5cuOS03U8cuQINm7cCKlUinr16mHEiBEiT25ccrqOL40cORJWVlaYO3euSBMbn5yuocHyRTBh\nf/31l9CnTx9BEAQhPpxGHhcAAATPSURBVD5e+PzzzwVBEASVSiV069ZNaNCgQca2fn5+wvXr1wWt\nViuMGDFCUCqVYoxslHK6jmFhYUKnTp0EQRAErVYrNG/eXHj27JkoMxubzNZwzJgxwokTJ17bTqFQ\nCM2aNROSkpKE1NRUoWXLlkJCQoIYIxulnK6jUqkUGjVqJCQnJws6nU7w8/MTbt++LcbIRimn6/jS\nmTNnhPbt2wtjxowpyDGN2vusoaHyxaRfIX/88ceoXr06AKBIkSJITU2FVqvF6tWr0aVLFyxYsAAA\nEBsbC6VSiSpVqgAAFi9eLNrMxiin6+jg4IC0tDSo1WpotVpIpVLY2tqKObrReNcavunq1auoVq0a\nHBwcAAA+Pj4IDQ2Fr69vgc5rrHK6jra2tjh48CDs7e0BAE5OTkhMTCzQWY1ZTtcRANRqNQIDAzFg\nwAD89ttvBTmmUcvpGhoyX0z6PWSZTAa5XA4A2LdvHz777DNERkbi1q1baNGiRcZ2jx49gqOjI8aO\nHQt/f39s3rxZpImNU07XsUSJEmjevDkaNWqERo0awd/fP+MXornLbA1lMhm2b9+OHj16YMSIEYiP\nj0dsbCxcXFwy7ufi4oKYmBixxjY6OV1HABk/e2FhYXj06BFq1Kgh2tzG5n3Wcc2aNejcuTP/X35D\nTtfQoPmSp9f0RuK3334T/Pz8hKSkJKFv377CgwcPBEEQhEaNGgmCIAiXL18WPv30UyE+Pl5QKpVC\n69athfDwcDFHNkrZrWNkZKTQvn17QalUCklJScKXX34pxMbGijmy0fnvGp49e1a4efOmIAiCsGbN\nGmHatGnCwYMHhVmzZmVsv3jxYmHXrl1ijWu0slvHl+7duye0atUq43Z6XXbreO/ePaFfv36CIAjC\nuXPneMg6E9mtoSHzxaRfIQP6Dx2tXr0a69atg1KpxN27dzF69Gh07NgRz549Q7du3eDq6ooKFSrA\n2dkZtra2qFWrFm7fvi326EYlJ+t47do11KhRA7a2tnBwcICXlxfCw8PFHt1o/HcNHRwcUK9ePVSq\nVAkA4Ovri/DwcLi7uyM2NjbjPs+ePYO7u7tYIxulnKwjAERHR2PQoEGYO3duxu30Sk7WMSQkBI8f\nP0bHjh0xbdr/27tDVYXhKI7jZ019BPEBDL6BmLRpEnFgEsWkYWCyeZNYrVafwWwWm8Eo6AMMRRCE\ncW64OLhchQljHi/fTxz/cPiV3w77w75ktVrJfD5/8+R2RMkw1n6J800iaefzWWu12tMt7b7Zqaq6\nrqu+72sQBOq6ru52u6TGNC9qjtvtVpvNpgZBoLfbTavVqh6PxyRHNetRhoPBQA+Hg6qqLhYLHY/H\ner1etVKp6Ol00svlEl7wwo+oOaqqdjodXa/Xb5nTuldyvGND/u2VDOPql4++1LVcLsX3ffE8L3w2\nnU4lm83+OTsajaTX64njOFIqlSSfzyc5qmlRcywUClIsFqXVaomISKPRkFwul+isVj3KsF6vi+d5\nkk6nJZPJyGQykVQqJcPhULrdrjiOI/1+P7zgheg57vd72Ww2MpvNwnPtdlvK5fI7xjYnao547pUM\n4+oXfr8IAIABH/8NGQCA/4BCBgDAAAoZAAADKGQAAAygkAEAMIBCBgDAAAoZAAADKGQAAAz4Bk8v\ndOjNfm9CAAAAAElFTkSuQmCC\n", + "text/plain": [ + "
\n", + "\n", + "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n", + "\n", + "Or better, do it yourself!" + ] + }, + { + "metadata": { + "id": "OZ5TY7B_4E_v", + "colab_type": "code", + "outputId": "5f7cfdb6-e69e-40ea-a4e1-4e0eca574301", + "colab": { + "base_uri": "https://localhost:8080/", + "height": 415 + } + }, + "cell_type": "code", + "source": [ + "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n", + " # YOUR CODE HERE\n", + "\n", + " x = tf.placeholder(tf.float32 , name = 'x')\n", + " y = tf.placeholder(tf.float32 , name = 'y')\n", + " W = tf.Variable(0.0 , name = 'Weight_1')\n", + " b = tf.Variable(0.0 , name = 'bias_1')\n", + " pred_y = (W*x) + b\n", + " loss = tf.reduce_mean(tf.square(y - pred_y))\n", + " optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)\n", + " with tf.Session() as sess:\n", + " sess.run(tf.global_variables_initializer())\n", + " \n", + " for epoch in range(n_epochs):\n", + " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n", + " \n", + " if epoch % interval == 0:\n", + " print ('Loss after epoch', epoch, ' is ', curr_loss)\n", + " \n", + " print ('Now testing the model in the test set')\n", + " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n", + " \n", + " print ('The final loss is: ', final_loss)\n", + " plt.plot(test_X[:10], test_Y[:10], 'g', label='True Function')\n", + " plt.plot(test_X[:10], final_preds[:10], 'r', label='Predicted Function')\n", + " plt.legend()\n", + " plt.show()\n", + "pass\n", + "linear_regression()" + ], + "execution_count": 21, + "outputs": [ + { + "output_type": "stream", + "text": [ + "Loss after epoch 0 is 48290.105\n", + "Loss after epoch 50 is 29.782778\n", + "Now testing the model in the test set\n", + "The final loss is: 33.2231\n" + ], + "name": "stdout" + }, + { + "output_type": "display_data", + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAFKCAYAAADMuCxnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XdYk+fbxvFvBgkkgKLi3nuLo63W\nDrXaWqsd1l2tWtx7oqjUvfeuVuuqs2ptta1dSrV2Kq66xYUbUEASEkjyvH+k5fe2tYoKPAGuz3F4\nCCQ8ObnNwWmSJ9etURRFQQghhBCq0qodQAghhBBSyEIIIYRHkEIWQgghPIAUshBCCOEBpJCFEEII\nDyCFLIQQQngAvZo3Hh19L0OPHxBg4u5da4beRnYna5g+ZB3Th6zjk5M1TB+Pu46BgX7/eVm2foSs\n1+vUjpDlyRqmD1nH9CHr+ORkDdNHRqxjti5kIYQQIquQQhZCCCE8gBSyEEII4QGkkIUQQggPIIUs\nhBBCeAApZCGEEMIDSCELIYQQHiBNg0FsNhvNmzenT58+1KtXj9DQUBwOB3q9npkzZxIYGEiVKlWo\nVatW6vesXr0anS7rvd9t4cK5nDlzijt3YrHZbBQuXAR//1xMmTIzXY7fqlUL8ucvgFb7v/8LLVq0\n/ImP++OPP/DMM8+SkBDPypXLCAkZ/cTHFEIIkXnSVMhLly4lV65cAMybN482bdrQrFkz1q9fz6pV\nqwgJCcHX15d169ZlaNjM0L//YAC+/HInFy5E0q/foHS/jVmzFmAymdL1mJs2radWrafImzeflLEQ\nQmRBDy3kyMhIzp8/T4MGDQAYO3YsRqMRgICAAE6cOJGhAT1FRMRBNm36GKvVSr9+gxk6tB9ffPE9\nAGPGhNCyZRsqVqzElCnjuXfvHk6nk0GDhlO2bLk0Hf+111761/EOHz6ExZLIlSuXuXbtKgMGDKVe\nvfrs3v0FW7duRqPR0K7dO6SkpHDy5B8MGzaAkSPDGD9+DCtXriMi4iDLly9Br9cTGJif0ND3+e67\nrzl27AhxcXe5cuUyHTp0onnzNzNs3YQQQqTNQwt5+vTphIWFsWPHDoDUR3ZOp5MNGzbQt29fAJKT\nkxk6dCjXrl3jlVdeoWvXrk8cbtxPY9gZueOxv1+r1eByKX/7WosybzLu2UmPdbzIyPNs3Lgdg8Fw\n38u3bNnIM888S4sWb3Lx4gXmz5/FvHlLHuu2/nL79i1mzVrAL7/8xGefbaNGjSBWr17BmjUbSU5O\nYfLksUybNocVKz5g1qwFxMfHpX7vrFlTmTt3MQUKFGTOnOl8++1uNBoNkZHn+eCDj7h6NYqxY0dJ\nIQshxH38duNXEpLjaFzilUy5vQcW8o4dOwgKCqJYsWJ/+7rT6SQkJIS6detSr149AEJCQnj99dfR\naDR07NiROnXqUK1atQfeeECA6YHzQE0+BrRaTVp/lvv65/ebfAwPHO79Fz8/b0ym/103d24TlStX\nokiRvABoNJrUy4xGL3LnNnHmzAnu3LnD3r3fAGC3J/3rtnQ6LaGhg1NfXw8ICGDBggX3PZ7ZbKRe\nvWcIDPSjQoVS2O1JxMffply5shQtGgjAypUfph43Xz5fdLoU9HotXl5O9HodVau6H6E3aPA8v//+\nO5UrV+app2pTsGBu/Py8SEqyPHQ90rJe4uFkHdOHrOOTkzX8b4qi8HXk10zZP4X9V/Zj8jKRGJqI\nRvPvLkrvdXxgIYeHhxMVFUV4eDg3b97EYDBQsGBBduzYQYkSJejXr1/qddu3b5/6cd26dTl79uxD\nC/lhO2WE1HyfkJrvp+XnuK/AQL/77iiVll2m7t2zYbUmp143Ls6KomhSP1cUJfVjiyUp9fL+/YdS\ntWr1/7wtp9PF1Klz//YacnT0vfsez2Kx4+XlQ3T0Pe7etZCc7CA+3obNlnzf48bEJBIfb8HhcBEb\na8HhcKZeLzY2AZvNwb17NpKTXURH38NqteJ0uh64Hv+1huLRyDqmD1nHJydreH8uxcWXF3YxP2I2\nR6MPA9C4+MsMfyqUmJjEf13/cdfxsXd7mjdvHtu2bWPLli20bt2aPn36EBMTg5eXFwMGDEi93oUL\nFxg6dCiKouBwOIiIiKBcubS9dppVaTQabDYbNpuNs2fPAFC5clX27QsH4OLFC2za9PETHe9+SpQo\nyZUrl7FardjtdgYN6oOiKGg0WpxOZ+r1/P390Wg03Lx5E4AjRyKoWLHSY/ykQgiRfaU4U9hyZiMv\nbHqG977uyLHoI7xe5i2+b/MjG5pvpWaB2pmW5ZH3Q96wYQN2u51OnToBUKZMGcaNG0fBggVp1aoV\nWq2WRo0aUb169YccKWt7881W9OjRmZIlS1OhgrvoWrVqy+TJ4+jTpxsul4tBg4Y90fHux8fHh+Dg\nXgwa1AeAtm07oNFoqFmzFn36BDN69LjU64aEjGH8+NHodDqKFCnKSy+9zDfffPV4P7AQQmQjNoeN\nTafXs+jwPK7cu4xeq6ddxXfoX3Mw5QLKq5JJoyiK8vCrZYyMftpEnpp5crKG6UPWMX3IOj65nL6G\niSmJrD2xiqVHFnLLehOjzsg7ld6lb82BFPMrnubjZMRT1o/8CFkIIYTIauJsd1lxfBkfHlvKXftd\nzF6+9A0aSK+gfhQwFVA7HiCFLIQQIhu7bb3NB0cXseqPFVhSEsltzM3wp0LpVq0nAd551I73N1LI\nQgghsp2r96JYfGQ+60+uxea0kd9UgGF1RtK5Sld8DZ75ti8pZCGEENlGZNw5FkTM5ZOzm3C4HBTz\nK06/moNoX7Ej3npvteM9kBSyEEKILO+PmOPMPzSbzyM/RUGhXO7yDKg1hJblWuOl81I7XppIIQsh\nhMiyfr/5K/MOzeLby18DUC1fDQbVHkazUs3RabPWjoNSyP9w48Z13n23HRUqVATcM7rfeaczL77Y\n8JGPtW3bZuLi4njhhQbs2xdOcHDP+17vr60Tvbwe/r+4CxfOM2fOjH9t2fjii89QrVqN1M/z5s3L\n+PFTHznzP+3evZvatetz7tyZB/4MQgiRWRRFYd/VcOYdmsWB6/sBeLpgXQbXHkaj4k3uO+YyK5BC\nvo/ixUukFl5CQjxdu75D3br1MBof7/WHcuUqUK5chf+8/K+tE9NSyP/F19c3XfZV/qfly5ezbFn9\nh/4MQgiR0VyKi68vfcX8Q7OIuH0IgIbFXmJQ7WHUK1xf5XRPTgr5Ifz9c5E3bz5iY2NZtepD9Hov\nEhLimDBhGjNmTOb69Ws4HA66detF7dpPcfDgbyxYMJs8efKSN28+ChcuQkTEQbZv38KkSTMeuHXi\n/PlL+fzzT/nuu91oNFqef74B7dt35PbtW4SFjcTLy4uyZdM+QebGjeuMGTOClSvd+1QHB3di0qTp\nfPTRcvLlC+TMmVPcunWT99+fRIUKFVm/fg3h4d+j0Wjp1asfp0+f5MyZM4waNZxWrdqm/gzff/8t\nmzevR6fTUaFCJQYNGsbKlcvuu1WkEEI8KYfLwWfnt7MgYg6n7pwEoFmpFgyqPZSg/LVUTpd+PLqQ\nzePGYNz5+NsvotWQ5x/bL9pbvIllXNq3X7xx4zoJCfHkz+9+47i/vz8jRoxm9+4vyJs3H6Gh7xMX\nF8fAgb1Ys2YTy5YtIixsIuXKlWfYsAEULlwk9VhWq+WBWydGR98mPPx7lixZCUDv3sE0bNiY7ds3\n89JLL9OmTXs+/ng158+fffw1+VNycjJz5ixix46t7N79BSaTifDw71m2bDXXr1/j449XM3JkGBs2\nrGXKlJlERBz882ewsnz5Ylat2oDJZCIkZHDqZf/cKlIKWQjxJOxOO5+c2cSCiDlcSriITqOjVfm2\nDKg1hIp5st9sfo8uZLVcuXKZfv16AGAwGBgzZjx6vXupKleuAsAffxzj6NHDHDt2BAC73U5KSgo3\nbtygXDn3o9igoFrY7fbU4166dJHixUtiNHpjNHozbdqcv93uqVMnuHo1iv793a/TWq0Wbt68zqVL\nF2nYsDEANWvW4ZdffvpX5sTExNTMAGXKlKVdu47/+TPWqFETgMDAApw8eYKzZ89QuXJVtFotRYsW\nY+TIsPt+X1TUFYoWLZ66W1XNmrU5e/Y0ANWrBwGQP39+EhP/vTuKEEKkhTXFyscnV7P4yAJuWK5j\n0Bp4t/J79Ks5kJK5SqkdL8N4dCFbxk16pEez/xQY6Medx5g1+v9fQ/4nvd4r9e93332PJk2a/u1y\nrfZ/G2j9c0y4VqtDUVz/ebt6vRf16tUnJGT0376+fv0aNBrtn8e8//ff7zXkmzdv/O1zh8OR+vFf\n+zH/lVOn0+JyPXysuUbz95/L4UjBaDTe95hCCPEoEuzxfPTHhyw7uphYWywmvYleNfrRu0Y/CvkW\nVjtehnvg9oviv1WuXJUff/wBgLt377Bs2WIA8uUL5MqVSyiKwuHDh/72PQ/bOrFChUpERBzCZrOh\nKArz5s3CbrdRvHgJTp92v27y19PDaWEymbl79w6KohAbG8P161f/87oVKlTi+PGjOBwO7tyJJTTU\nvVPVP4u1WLESXL16BavVAsDhwxFUqFA5zZmEEOKfYpJimPLLBGquq8KUXyeQ4nIwpPZwDnU6wYT6\nU3JEGYOHP0L2ZI0aNSYi4nd69XoPp9PJe++5ny7u0aMPY8aMoGDBQqmvO//lYVsnLly4nDZt2tO3\nb3e0Wi0vvNAAo9Gb1q3bExY2kn379lKmTNr3mfb396dOnafp1u1dypYt98CzpAsVKswrrzSjX78e\nKIpCz559AahUqRLdu79L794DUn+Gvn0HMnRofzQaLdWrB1GjRhAHD/76SOsnhBDXE6+x5MgC1p1c\nTZIjiXw++RhYdxxdq3bDz+CvdrxMJ9svigeSNUwfso7pQ9bxyXnCGl6Ij2Tx4flsOr2eFFcKRXyL\n0jdoAB0qvYvJy6RqtrSS7ReFEEJkWadiTzI/YjY7zm/DpbgonasMA2oNoVX5thh0BrXjqU4KWQgh\nRIZwKS7+iDlGeNQe9lz5jp+u/whA5bxVGVRrKC3KvJnlxltmJClkIYQQ6eam5QbhUXsIj/qeH6L2\nEmuLTb3s6YJ16V9rMC+XaJplx1tmJClkIYQQjy3JkcTP1w8QHrWHH6L2pE7SAihoLkS7iu/QoFgj\nXijakHw++VRM6vmkkIUQQqSZoiicjD2R+ij4lxs/YXe6ByD56H1oVLwxDYo1okGxl6gQUFEeCT8C\nKWQhhBAPdNt6m31X9/5Zwnu4bb2VelmVvNX+LOBGPFOoHt76x9uER0ghCyGE+Ae7085vN35hb9T3\nhEft4Y+YY6mX5fMJpFX5tjQo1ogXizakgLmgikmzFylkIYTI4RRF4ezdM4T/WcA/Xf+RJEcSAAat\ngeeLNqBBsUY0LPYSlfNWQauRIY8ZQQpZCCFyoDu2WPZFhac+DX3dci31sgoBFWlQ/CUaFmtE3UL1\ns8ywjqxOClkIIXKAZGcyh279zm/Hf+TLM19x5PZhFNyDGvN45+Gtsm/ToNhLvFisIYV9izzkaCIj\nSCELIUQ2pCgKF+Mj2fvn25H2X9uHJcW9Lapeq6de4fqpJ2NVDwySp6E9gBSyEEJkE/H2OPZf3cfe\nqO/5IWoPV+5dTr2sTO6yNCjWiDertqCKuRa+hv+eqSzUIYUshBBZlMPl4PDtQ+y94j4ZK+L2QVx/\n7pmey5ibFmXeTD0burh/CcAzNpcQ9yeFLIQQWUiSI4nPz3/K7ktfsv/qDyQkxwOg0+ioU+Dp1Keh\ng/LXQq+VX/FZifxrCSFEFnAh7jyrT3zEptMfE2ePA6C4f0neKteKBsUa8VyR58llzK1ySvEkpJCF\nEMJDOVwOvr70Fav/WMEPV/cC7sEcg2oNo13FDpTOXVblhCI9SSELIYSHuWm5wccn17Du5GpuWK4D\nUK9wfbpUCea10q/L3sHZlBSyEEJ4AEVR+PHaPlb9sYKvLu7CqTjx9fLjvard6VwlmEp5K6sdUWQw\nKWQhhFBRnO0um89sYM2Jjzgfdw5wb9jQtWo3WpZvja+Xr8oJRWaRQhZCCBUcuR3B6j9W8un5rSQ5\nkjBoDbQu344uVYOpU+Bp2bYwB5JCFkKITGJNsfLZ+e2sPrGCw7cjACjhX5LOVYJpX7EjeX3yqpxQ\nqEkKWQghMtj5u+dYc2Ilm85sIN4eh1ajpWnJZnSp2o0GxRrJ2EoBSCELIUSGSHGmsPvSl6w+sZL9\nV8MBCPTJz+Daw+hUuStF/YqpG1B4HClkIYRIRzcSr7Pu5Go+PrWGm5YbANQv/Dxdqgbzaqnm8pYl\n8Z+kkIUQ4gm5FBf7r/7A6hMr2X3xC5yKEz+DP92q9aRzlWAq5KmodkSRBUghCyHEY7pru8Om0xtY\nc2IlF+IjAaiWrwZdqgbTslxrzF5mlROKrEQKWQghHoGiKBy+fYjVJ1ay49w2bE4bRp2RNhXa07Vq\nN2rlryNvWRKPRQpZCCHSwJpi5dNzW1l1YgXHoo8AUCpXaTpXCaZdxQ7k8Za3LIknI4UshBAPcO7u\nWfdblk5vICE5Hq1Gy6ulmtOlSjAvFmsob1kS6UYKWQgh/iHFmcJXF3ex+sRKfry2D4D8pgJ0q96T\nTpW6UMSvqMoJRXYkhSyEEH+6nniNtSdXsf7kWm5ZbwLwXJEX6Fq1G01LvoaXzkvlhCI7k0IWQuRo\nLsXFD1F7WX1iJV9f+hKX4sLfkIse1XvTuUow5QLKqx1R5BBSyEKIHOuu7Q5td77FkejDANQIrEmX\nKsG8We5tecuSyHRSyEKIHMmaYqXTl+04En2YZqVaMLDWEGoWqK12LJGDSSELIXIch8tBj2+68NvN\nX2hZrhVLGq+Qs6WF6uQeKITIURRFYWj4AL65vJsXizZkQaMPpIyFR5B7oRAiR5n8y3g2nv6YoMCa\nrGr6sWz2IDyGFLIQIsdYdnQxCw7PoXSuMmxovg1fg5/akYRIJYUshMgRtp3dQtiBUAqYCrKlxQ7y\n+eRTO5IQfyOFLITI9vZe+Z7+e3rhb8jFpubbKe5fQu1IIgvQ3L2D9vKlTLs9KWQhRLYWcesgXXd3\nRKfRsa7ZJqrkq6p2JOHhNAnxmKZNIk+tquR5sS4oSqbcbpoK2Waz0bhxY7Zv386NGzfo0qULHTt2\npEuXLkRHRwPw+eef8/bbb9O6dWs++eSTDA0thBBpcf7uOd75ojU2ZxLLmqyiXuH6akcSnsxiwWfB\nXPLUqYZ5zgwwmbg3bTZk0naaaSrkpUuXkitXLgDmzZtHmzZt+Pjjj2nSpAmrVq3CarWyePFiVq9e\nzbp161izZg1xcXEZGlwIIR7kpuUGbXe9RawtllkvzqdZ6eZqRxKeym7He+Uy8j5dA99JYwFIHDOO\n2N+OYm/3TqbFeOhgkMjISM6fP0+DBg0AGDt2LEajEYCAgABOnDjB0aNHqVatGn5+7jMWa9WqRURE\nBI0aNcq45EII8R/i7XG03fkWUfeuEPp0GB0rd1Y7kvBEDgfGTzZhnjkV3dUoFJMZy5DhJPXuj5Ir\nd6bHeegj5OnTpzNy5MjUz00mEzqdDqfTyYYNG2jRogUxMTHkyZMn9Tp58uRJfSpbCCEyU5IjiY5f\ntuXUnZMEV+vBoNrD1I4kPI3LhfGz7QS88Az+A/ugjb6NtWdfYn8/hnVkmCplDA95hLxjxw6CgoIo\nVqzY377udDoJCQmhbt261KtXj507d/7tciWNL4AHBJjQ63WPGPnRBAbK+wyflKxh+pB1TB8PWkeH\ny0G3LR359cbPtKnShuVvLZUpXPeRY++LigJffgmjR8PRo6DXQ48eaMLCMBUtiukRD5fe6/jAQg4P\nDycqKorw8HBu3ryJwWCgYMGC7NixgxIlStCvXz8A8ufPT0xMTOr33b59m6CgoIfe+N271ieM/2CB\ngX5ER9/L0NvI7mQN04esY/p40DoqisKQ8P58fuZzni/agNnPLSY2xpLJCT1fTr0veh3Yj3nyeLwO\n/oai0WBv1RbL8FBcpUq7r/CIa/K46/igEn9gIc+bNy/144ULF1KkSBFiYmLw8vJiwIABqZfVqFGD\nMWPGkJCQgE6nIyIiglGjRj1yUCGEeFzTfpvI+lNrqRFYkzVN12PUGdWOJDyAPuIg5ikTMezbC4C9\nWQssI0bjrFRZ5WT/9si7PW3YsAG73U6nTp0AKFOmDOPGjWPo0KEEBwej0Wjo27dv6gleQgiR0VYc\n+4C5h2ZRKldpNry2VUZiCnQnT2CeNgnj7i8ASG7QCEtoGI6anrvFpkZJ6wu+GSCjnzbJqU/NpCdZ\nw/Qh65g+7reOn57bSq9vgwk05eeLlt9Swr+kOuGyiOx+X9ReiMQ8YwrGT7eiURRSnq6LZdT7pDz7\nXLreTqY/ZS2EEJ4sPGoP/b7via/Bj03Nt0sZ52Daa1cxzZmB94Z1aJxOUqrVwBo6huSXXs60wR5P\nSgpZCJElHbkdQdfdHdFqtKx7dRNV81VTO5JQgSY6GtOC2fisXonGbsdRrjyWEaNJbv4GaLPWGfZS\nyEKILOdC3Hk6fNGKJIeVFS+v5dki6ft0pPB8mvg4fJYswLRsKRqrBWex4liGh2Jv1db9dqYsKGum\nFkLkWLcsN2mz8y1ikmKY+eI8mpd5Xe1IIjNZLPis+ADTovlo4+Nw5i+ANWw8to6dwZi1z6yXQhZC\nZBlxtjja7mrJlXuXCXlqFJ2rvKd2JJFZ7HZ81n6Eae4stDHRuAICSAybQFJwDzA96kgPzySFLITI\nEmwOG602teJk7B90rdqNoXVGqB1JZAaHA+/NGzDNmobu2lVcZl8sQ0eQ1Lsfin8utdOlKylkIYTH\nc7qc9Po2mH2X99GizJtMeW4mmixy5qx4TH/OmzZNn4z+QiSKtzfWPgOw9h+Mkjev2ukyhBSyEMKj\nKYpCyL4hfHlxJ41KNWJJ4w/RaTN2Br5QkaJg+GY35qkT0Z/8A0WvJ6lzMNYhw3EVKqx2ugwlhSyE\n8GjTf5/MupOrqJqvOp+2/RR7gjwyzq689v+Aecp4vA4dRNFosLVu5543XbKU2tEyhRSyEMJjrTy+\nnDkHZ1DCvyQbm2/D3+hPNNl3ylROpT/4G+apEzHs/wEA+2uvu+dNV6ykcrLMJYUshPBIn53fzqj9\nw8nnE8iWFjsoYCqgdiSRznQn/sA8bSLGr78CILnhS+5500G1VE6mDilkIYTH2Xc1nD7fdcfs5cvm\n5tsplau02pFEOtJFnsM0Ywren24DIOWZeu550/Xqq5xMXVLIQgiPciz6CJ2/6oAGDWte3UC1wBpq\nRxLpRHs1CtPs6XhvWu+eN109CMuoMFIaNs4y86YzkhSyEMJjXIiPpN2ut7GmWFjxyhqeL/qi2pFE\nOtDcvo1p/ix81nyEJjkZR/kKWEaMIbn561LE/48UshDCI9yy3qLtzreISYpm+gtzaFHmTbUjiSek\nibuLafECfD5cisZqxVm8xP/mTevkrWv/JIUshFBdgj2edjtbcjnhEkPrjKBr1W5qRxJPIjER04dL\n8Vm8AG1CPM4CBbG+P9E9b9pgUDudx5JCFkKoyuaw0fmrDpyIPc67ld8j5KlRakcSj8tmw2fNSkzz\nZ6ONiXHPmx47iaSu3bLNvOmMJIUshFCN0+Wkz3fdOXB9P6+Vfp3pL8yWkZhZUUoK3pvWY5o9Hd31\na7h8/bAMDyWpV18UP3+102UZUshCCFUoisLI/cPYdeEzni38HEsbr5CRmFmNy4Xx062YZkxBf/GC\ne95034FY+w9CyZM9501nJClkIYQqZh2cxpoTK6mStxprX92It95b7UgirRQFw+4vMU+bhP7UCRQv\nL5K6dsM6eDiugoXUTpdlSSELITLd6j9WMvP3qRT3L8mm5tvwN2avbfSyLUXBa1845qkT8Io4hKLV\nYmvbAcuwkbhKlFQ7XZYnhSyEyFQ7I3cwYt8Q8vnkY0vz7RQwF1Q7kkgD/W+/Yp46AcOB/QDYW7zp\nnjddvoLKybIPKWQhRKb58do+en/bDZOXmY2vbaN07rJqRxIPoTt+zD1v+tuvAbC/1ARraBiO6kEq\nJ8t+pJCFEJniePRR3v2yPQoKq5uup0b+mmpHEg+gO38O0/TJeH+2HYDkevWxhL6Po249lZNlX1LI\nQogMdzH+Au12vY0lJZHlL6/ixWIN1Y4k/oM26gqmWdPw3rwBjctFSo2a7o0fGjSSMZcZTApZCJGh\nbltv03bnW0Qn3Wbq8zN5o2xLtSOJ+9DcuoV53ky8165Ck5KCo0JFLCPDSG7WXIo4k0ghCyEyzL3k\nBNrveptLCRcZUns4wdV6qh1J/IPm7h1Mi+bjs+IDNElJOEuUxBIyCnvL1jJvOpNJIQshMoTdaafL\nV+9wPOYonSp3YcTTY9SOJP4fTeI9fJYtwWfJQrT3EnAWKox1wlRsHTqBl5fa8XIkKWQhRLr7ayTm\n/ms/8Gqp5kx/YY6MxPQUSUn4LF2EacFstLGxuPLmJXH8FJK6BIOPj9rpcjQpZCFEulIUhVE/Dmdn\n5A7qFnqWD5qsRK+VXzWqS0nBe8M6mDcT32vXcPn5YxkxmqSefVB8/dROJ5BCFkKkszmHZrDqjxVU\nylOFdc024aOXR12qcjoxbv8E84wp6C5fAh8frP0HY+03ECUgj9rpxP8jhSyEeCiny4ndaSfZacf+\nrz82kp3J2Bw2jtyOYPpvkynuV4LNLbaTy5hb7eg5l6Jg+HIX5umT0J8+5Z43HdwDn4njsOh91U4n\n7kMKWQgP9lcRppbe3/62Y3f8rxiTnfbUy+1OG3ZnMnaHDbvrr+v9+bU/v9f2V8E+7BhOGw6XI82Z\n83rnZXOL7RQ0yyYDqlAUvML3uOdNHzmMotWS1L4j1qEjcBUvgU+gH0TfUzuluA8pZCE80K83fqHn\nN125brmWKbfnpfXCoDPirTNi0Bkx6oz4G/wx6r0xaA14670x6AwYdd4Y//z7b9fXGzFqjRj13rxa\n6jVK5SqdKbnF3+l/+dk9b/rnAwDY3miJNWQUznLlVU4m0kIKWQgP88WFnfT+NpgUVwr1Cz//Zxn+\n/7L8sxT/LElvnfefBen+2KAzpH6P8f/9cR/jz2LVe2PU/vm3zohWo1X7xxZPQH/8KKapEzF+9w0A\n9iavYBkZhrNadZWTiUchhSwnjy/jAAAgAElEQVSEB1l5fDmj9g/HR29i/WvraVS8idqRhAfTnTvr\nnjf9+acAJNd/3j1v+ulnVE4mHocUshAewKW4mPzLeBYenks+n0A2vrZVNl8Q/0l75TLmWdMwbtno\nnjddsxaWUWNJeaGBjLnMwqSQhVBZsjOZQXv7svXsZkrnKsOm5tspmauU2rGEB9Leuolp7ky81612\nz5uuVNk9b7ppMynibEAKWQgV3UtOoOvuTuy7upfaBZ7i42ZbyOuTV+1YwsNo7sS6502vXOaeN12y\nlHve9FutZN50NiKFLIRKblpu0H5XK07EHqdpyWZ80OQjTF4mtWMJD6K5l+CeN710kXvedOEiWCeN\nwNbuHZk3nQ1JIQuhgrN3ztBuV0uuJkbRuUowU5+fKeMlxf8kJeGzaoV73vSdO7jy5SMxZCpJnYPB\n21vtdCKDyG8AITLZLzd+5t0v2xJnj2PUM+8zsNZQ2XhBuCUn471+Laa5M9HdvIHLPxeW0DCs3XuD\nr0zXyu6kkIXIRLsiP6f3d8E4FScLGi2lXcV31I4kPIHTiXHrZswzp6G7cgnFZMI6cCjWvgNQcgeo\nnU5kEilkITLJimMfMPrHEZi8zKx9ZRMNi7+kdiShNkXBsOtzzDMmoz9zGsVgwNq9F9aBw1Dy51c7\nnchkUshCZDCX4iLk2xBm/jSTQJ/8bGy+leqBQWrHEmpSFLz2fod56iS8jh5G0elIeudd97zposXU\nTidUIoUsRAZKdiYzYE9vtp/7hLK5y7Gx+TZK+JdUO5ZQkdcvP2GaMgHDLz8BYHvrbfe86TLlVE4m\n1CaFLEQGSbDH0/XrTuy/Gk69ovVY9fIG8njLe4xzKv3Rw5inTsSw5zsA7K+8imXEGJxVq6mcTHgK\nKWQhMsCNxOu0/6IVJ2P/4NVSzdnWfguJcWnfwlBkH7ozpzFPn4xx12cAJD//IpbQMBx1nlY5mfA0\nUshCpLMzd07TbldLriVepWvVbkx5biY+Xj4kInvQ5iTaSxfd86a3bnbPm65dB0vo++5500LchxSy\nEOnol+s/0emrdsTb4xhTdxz9aw6W9xjnMNqbNzDNmYH3x2vQOBw4KlXBMup9kl9uKvOmxQNJIQuR\nTnZG7qDPd91xKk4WvbSMNhXaqx1JZCJNbCymhXPx+Wg5GpsNR+kyWEeMxv5GS9DKftPi4aSQhUgH\ny48uIexAKCYvM+uabqZBsUZqRxKZRJMQj8/SRfgsW4I28R7OIkWxDhuJrW0H0MuvWJF2cm8R4gm4\nFBcTfn6fJUcWkN9UgI3Nt1EtX3W1Y4nMYLXis3I5pkVz0d69iytfIImhY0jq1FXmTYvHIoUsxGOy\nO+0M+L4Xn57fRrnc5dnYfBvF/UuoHUtktORkvD9eg2nODHS3b+HKlZvE0WNJCu4p86bFE5FCFuIx\nxNvj6Lq7Iz9e28fTBeuyrtkmArzzqB1LZCSnE+MnmzDPmobuymUUkxnL4GEk9RmAkiu32ulENiCF\nLMQjup54jfa73ubUnZM0K9WCpU1W4KP3UTuWyCguF4YvPsc8bRL6c2fd86Z79sE6YChKYKDa6UQ2\nkqZT/2w2G40bN2b79u0ArF27lipVqmCxWFKvU6VKFTp16pT6x+l0ZkxiIVR0+s4pmm1rzKk7Jwmu\n1oOVr6yVMs6uFAXD99+Qu8mL5Ap+F92FSJI6deHOr0ewTJwmZSzSXZoeIS9dupRcuXIBsGPHDmJj\nY8n/j51IfH19WbduXfonFMJD/HTtRzrv7kC8PY6wehPoFzRQ3mOcTXn9fADz5PF4/fYLikaDrWVr\nrCGhOEuXVTuayMYeWsiRkZGcP3+eBg0aANC4cWN8fX3ZuXNnRmcTwmN8dn47fb/rgYLCksYf0qp8\nW7UjiQygPxKBecoEDOF7ALA3fQ3LyDE4K1dRN5jIER76lPX06dMZOXJk6ue+/3EWYXJyMkOHDqVd\nu3asWrUq/RIKobIPji6i+zddMOiMbGy+Tco4G9KdPoV/l3cIeLkBhvA9JL/QkLtffU/C2o1SxiLT\nPPAR8o4dOwgKCqJYsYfvzxkSEsLrr7+ORqOhY8eO1KlTh2rVHryLSUCACb1e92iJH1FgoF+GHj8n\nyKlr6FJcDP9mOHN+mUMh30J89c5X1ChY47GPl1PXMb2l6zpGRsK4cbB+PSgK1KsHkydjaNgQQ/rd\niseR+2L6SO91fGAhh4eHExUVRXh4ODdv3sRgMFCwYEGeffbZf123ffv/jQmsW7cuZ8+efWgh371r\nfczYaRMY6Ed0tAz0fxI5dQ3tTjv9v+/JjvPbKR9QgY3Nt1FYV/yx1yKnrmN6S6911N64jmn2DLw3\nrHXPm65SDcuoMJIbv+KeN52N/63kvpg+HncdH1TiDyzkefPmpX68cOFCihQpct8yvnDhAosXL2bW\nrFk4nU4iIiJo2rTpIwcVwhPE2+Po/FUHfrr+I88UqsfaVzfKe4yzCU1MDKYFc/BZ9SEaux1HmbJY\nR47B3uJNmTctVPfI70NeunQpP/30E9HR0XTv3p2goCBCQkIoWLAgrVq1QqvV0qhRI6pXl/GBIuu5\ndu8q7b94m9N3TtG89Bssafwh3noZg5jVaRLi8Vmy0D1v2pKIs2gxLMNDsbduJ/OmhcfQKIqiqHXj\nGf20iTw18+Ry0hqejD1B+11vc8Nyne7VejGh/lR02vQ5xyEnrWNGeuR1tFj+N286Lg5XYH4sg4dh\n69QVjMaMC+rB5L6YPjL9KWshcooD1/bT+asOJCTHM7beJPoE9Zf3GGdldjveH6/GPGcm2ujbuHLn\nJnHMOPe8abNZ7XRC3JcUssjxPj23lf7f90JBYWnjFbxdvo3akcTjcjjc86ZnTkV3Nco9b3rIcJJ6\n95d508LjSSGLHG3pkUWM/WkUfgZ/Vjddz/NFX1Q7kngcLhfGnTswTZ+M/vw5FKMRa8++WAcMkRGX\nIsuQQhY5kktxMfbAKJYdW0JBcyE2vraNKvmqqh1LPCpFwfDd15inTER/4jiKXk9Sp65Yh4bgKlxE\n7XRCPBIpZJHj2Bw2+n/fi88it1MhoCIbm2+jqN/Dh98Iz+J1YL973vTB39zzplu1xTI8FFep0mpH\nE+KxSCGLHCXOdpfOuzvw8/UD1CtcnzVNN5DbO0DtWOIR6CMOYp4yEcO+vQDYm7XAMmI0zkqVVU4m\nxJORQhY5xrV7V2m3qyVn7p7m9TJvseilZfIe4yxEd/IEzJ1GwGefAZDcoBGW0DAcNWurnEyI9CGF\nLHKEEzF/0P6Lt7lpuUHP6n0YX38KWo1MZsoKtBciMc+YgvHTraAopDxdF8uo90l59jm1owmRrqSQ\nRbYWb49jxfFlLD68gMSUe4x/dgq9g/qpHUukgfbaVUxzZuC9YR0ap5OUqtXxmj6VuDrPuedNC5HN\nSCGLbOmu7Q7Lji1hxbFlJCTHE2AMYHmTVbxZ7m21o4mH0ERHY1owG5/VK93zpsuWwzJyDMnN3yCw\nQK5svfGDyNmkkEW2EpMUwwdHFrHyj+VYUhLJ55OPsHoT6FolGF+DbDnnyTTxcfgsWYBp2VI0VgvO\nYsXd86ZbtZV50yJHkHu5yBZuWW6y+MgC1p74CKvDSn5TAUY8PYpOlbti9pJRiR7NYsFnxQeYFs1H\nGx+HM38BrGHjsXXsnGPnTYucSQpZZGnXE6+x6PA81p1cjd1pp7C5CGH1xtOh0rv46H3UjicexG7H\nZ+1HmObOQhsT7Z43HTaBpOAeYDKpnU6ITCeFLLKkKwmXWRAxl02nPybZlUxxvxIMqDWEthU7YNTJ\noyqP5nDgvXkDplnT0F27isvsi2XoCJJ690Pxz6V2OiFUI4UsspQL8ZEsODSHLWc34nA5KJWrNINq\nDaNV+bZ46bzUjicexOXC+Nl297zpC5Eo3t5Ye/fH2n8wSr58aqcTQnVSyCJLOHf3LPMOzWLbuS24\nFBflcpdnUO1hvFWuFXqt3I09mqJg+GY35qkT0Z/8wz1vunMw1iHDcRUqrHY6ITyG/CYTHu1U7Enm\nHprBZ+c/RUGhUp7KDKkTQvPSb6DT6tSOJx7Ca/8PmKeMx+vQQfe86dbt3POmS5ZSO5oQHkcKWXik\n49FHmXNoJl9c+ByAavlqMKROCK+Wek0mbGUB+oO/YZ46EcP+HwCwv/a6e950xUoqJxPCc0khC48S\ncesgcw7O4JvLuwGolb82Q+qE0KREUzQyncnj6U78gXnaRIxffwVAcsOX3POmg2qpnEwIzyeFLDzC\nrzd+Yc7B6eyN+h6ApwvWZWidETQo1kiKOAvQRZ7DNGMK3p9uAyDlmXruedP16qucTIisQwpZqEZR\nFH66/iNzDs5g/zX3U5vPFXmBIXVCqF/4eSniLEB7NQrT7Ol4b1rvnjddrQbWUWEkN2oi86aFeERS\nyCLTKYrCD1f3MvvgdH698TMADYo1YkidEdQtVE/ldCItNLdvY5o/C581H6FJTsZRrrx73vRrr4NW\nXuMX4nFIIYtMoygK313+mjmHZnDo1kEAXi7RlMF1hlO7wFMqpxNpoYm7i2nxAnw+XIrGasVZvASW\nYSOxt24HOjnrXYgnIYUsMpxLcbH74pfMOTSDY9FHAGhWqgVD6gynemCQyulEmiQmYvpwKT6LF6BN\niMdZoCDW9ye6500bDGqnEyJbkEIWGcbpcrLrwmfMOTiTU3dOoEHDG2VaMrjOcCrnraJ2PJEWNhs+\na1Zimj8bbUwMroAAEt+fSNJ73WXetBDpTApZpDuHy8GO89uYd2gWZ++eQavR0qp8WwbVGkb5PBXU\njifSIiUF703rMc2eju76NVy+fliGh5LUqy+Kn7/a6YTIlqSQRbpJcaaw7dwW5h6aycX4C+i1etpX\n7MjAWkMonbus2vFEWrhcGD/dinn6ZHSXLrrnTfcdiLX/IJQ8edVOJ0S2JoUsnliyM5lNp9ezIGIO\nV+5dxkvrRafKXRlQazAl/EuqHU+khaJg2P0l5mmT0J86geLlRVLXblgHD8dVsJDa6YTIEaSQxWOz\nOWysP7WWRYfncS3xKkadkeBqPegXNIgifkXVjifSQlHw2heOeeoEvCIOoWi12Np2wDJsJK4SJdVO\nJ0SOIoUsHpk1xcq6k6tYdHg+t6w38dH70LNGX/oFDaSAuaDa8UQa6X/7FfPUCRgO7AfA3uJN97zp\n8vI6vxBqkEIWj2RX5OeE7BtMTFI0Jr2Z/jUH06tGPwJNgWpHE2mkO37MPW/6268BsL/UBGtoGI7q\n8hY0IdQkhSzSJMmRxPsHRrHmxEp89D4MqT2cHjX6kMdbTvTJKnTnz2GaPhnvz7YDkFyvPpbQ93HU\nleloQngCKWTxUKfvnKLnN105decklfJUZvnLq6mQp6LasUQaaaOuYJo1De/NG9C4XKTUqOne+KFB\nI5k3LYQHkUIW/0lRFD489CEDdw8kyZFElyrBjK8/BR+9j9rRRBpobt3CPG8m3mtXoUlJwVGhIpaR\nYSQ3ay5FLIQHkkIW9xVvj2No+EA+j/yUXMbcLH7pQ5qXeV3tWCINNHfvYFo0H58VH6BJSsJZoiSW\nkFHYW7aWedNCeDApZPEvB2/+Rq9vg7ly7zL1i9VnQYNlFPMrrnYs8RCaxHv4LFuCz5KFaO8l4CxU\nGOuEqdg6dAIvL7XjCSEeQgpZpHIpLhYdnsfUXyfiUlwMqRPC9Fcnczc2Se1o4kGSkvBZvRLTgtlo\nY2Nx5c1L4vgpJHUJBh95eUGIrEIKWQBwy3qLvt/1YN/VvRQ0F2JJ4w95rsgL6LVyF/FYKSl4b1iH\nac4MdDeu4/LzxzJiNEk9+6D4+qmdTgjxiOS3rWDPlW/p931PYpJieLlEU+Y3WkpeH3k7k8dyOjFu\n/wTzjCnoLl9C8fHB2n8w1n4DUQLyqJ1OCPGYpJBzsGRnMlN+ncCSIwswaA1Mqj+N7tV7o5EzcD2T\nomD4chfm6ZPQnz7lnjcd3AProGG4CsiENCGyOinkHOpi/AV6ffseh29HUDpXGZa/vIrqgTKpySMp\nCl7he9zzpo8cRtFqSWrfEevQEbiKl1A7nRAinUgh50Dbz33CsPBBJKbco02F9kx7fha+BnnN0RPp\nf/nZPW/65wMA2N5oiTVkFM5y5VVOJoRIb1LIOYglxcKo/cPZePpjzF6+LH5pOa0rtFM7lrgP/fGj\nmKZOxPjdNwDYm7yCZWQYzmrVVU4mhMgoUsg5xPGYY/T8pivn485RPTCI5U0+onTusmrHEv+gO3sG\n8/TJGHfuACC5/vPuedNPP6NyMiFERpNCzuYUReGjP5Yz9sBokl3J9KzRlzF1x2HUGdWOJv4f7ZXL\nmGdNw7hlo3vedM1aWEaNJeWFBjLmUogcQgo5G7tji2XQ3n7svvgFeb3zsvClD2hc4hW1Y4n/R3vr\nJqa5M/Fet9o9b7pSZfe86abNpIiFyGGkkLOpn68foPe33bhuucZzRV5gSeMPKWgupHYs8SfNnVj3\nvOmVy9AkJeEoVRpryCjsb74t86aFyKGkkLMZp8vJnEMzmH1wOho0hD4dxoBaQ9Bp5Ze8J9DcS3DP\nm166yD1vunARrJNGYGv3jsybFiKHk0LORq4nXqP3d934+foBivoW44MmH/F0ITkZyCMkJeGzZKF7\n3vSdO7jy5SMxZCpJnYPB21vtdEIIDyCFnE3svvglA/f05q79Ls1Lv8GcBgvI7R2gdiyRnIz3+rUw\nfxa+16/j8s+FJTQMa/fe4OurdjohhAeRQs7ibA4bE34OY8XxZXjrvJnxwlw6V3lPxl+qzenEuHUz\n5pnT0F25BCYT1oFDsfYdgJJb/qMkhPg3KeQs7Pzdc3T/pgsnYo9TIaAiy19eTaW8ldWOlbMpCoZd\nn2OeMRn9mdMoBgPW7r0wTRyHRWtSO50QwoNJIWdBiqKw6fR6QvcPw+qw0qlyVybWn4rJS37hq0ZR\n8Nr7Heapk/A6ehhFpyPpnXfd86aLFsMU6AfR99ROKYTwYFLIWcy95ASG/zCY7ec+wd+QixUvr+H1\nsm+pHStH8/rlJ0xTJmD45ScAbG+97Z43XaacysmEEFmJFHIWcvjWIXp++x6XEi5Su8BTLGvyEcX9\nZbcfteiPHsY8dSKGPd8BYH/lVSwjxuCsWk3lZEKIrEgKOQtwKS6WHlnE5F/H4XQ5GVhrKCFPjcJL\nJ+9bVYPuzGn3vOldnwGQ/PyLWELDcNR5WuVkQoisTJuWK9lsNho3bsz27dsBWLt2LVWqVMFisaRe\n5/PPP+ftt9+mdevWfPLJJxmTNgeKtkbT4YtWjP95DHm887KlxQ5G1x0rZawC7aWL+PXrScCLdTHu\n+oyU2nWI2/o58dt2ShkLIZ5Ymh4hL126lFy5cgGwY8cOYmNjyZ8/f+rlVquVxYsXs3XrVry8vGjV\nqhVNmjQhd+7cGZM6h/ghai99v+/BbestGhVvzMJGywg0BaodK8fR3ryBac4MvD9eg8bhwFGpCpZR\n75P8clOZNy2ESDcPLeTIyEjOnz9PgwYNAGjcuDG+vr7s3Lkz9TpHjx6lWrVq+Pm5N7mvVasWERER\nNGrUKGNSZ3MpzhSm/zaZhYfnotfqGffsZHrV6ItWk6YnNEQ60cTGYlo4F5+PlqOx2XCULoN1xGjs\nb7QErfxbCCHS10MLefr06YSFhbFjh3t/Vt/7TBeKiYkhT548qZ/nyZOH6OjodIyZc1xJuEzPb9/j\n0K3fKelfiuUvryIofy21Y+UomoR4fJYuwmfZErSJ93AWKYp12EhsbTuAXk67EEJkjAf+dtmxYwdB\nQUEUK1bskQ6qKEqarhcQYEKvz9hNDwID/TL0+OnpkxOf0H1nd+Lt8XSo1oGlry3F3+ivdqwstYZP\nxGqFRYtg+nS4cwfy54fJk9D16IGftzdPugo5Zh0zmKzjk5M1TB/pvY4PLOTw8HCioqIIDw/n5s2b\nGAwGChYsyLPPPvu36+XPn5+YmJjUz2/fvk1QUNBDb/zuXetjxk6bwEA/orPAMAZripWwAyNZd3I1\nJr2JBY2W0rZCB+wJGqJRN39WWcMnkpyM97rVmObORHf7Fq5cubGOHktScE/3vOl7Ke4/TyBHrGMm\nkHV8crKG6eNx1/FBJf7AQp43b17qxwsXLqRIkSL/KmOAGjVqMGbMGBISEtDpdERERDBq1KhHDpoT\nnYo9SY9vunDm7mmq5qvO8iarKBsgAyUyhcPhnjc9axq6K5dRTGYsg4eR1GcASi45IVEIkbke+QWx\npUuX8tNPPxEdHU337t0JCgoiJCSEoUOHEhwcjEajoW/fvqkneIl/UxSF327+ypYzG/jkzCZsThvd\nq/UirN4EvPWyFV+Gc7kwfPE55mmT0J8765433bMP1gFDUQLlLHYhhDo0Slpf8M0AGf20iac9NRN1\n7wpbzmxky5mNXIy/AEBhcxGmvTCbpqWaqZzu/jxtDZ+IomDY8y2mKRPxOn4URafD1qET1iEhuIoU\nzdCbzlbrqCJZxycna5g+Mv0pa/HkElMS2RX5GVvObOTHa/sA8NH78Ha5NrSt2IHni7yITpuxJ7YJ\n8Pr5AObJ4/H67RcUjQZby9ZYQ0Jxli6rdjQhhACkkDOES3Fx4Np+Np/ZwK7Iz7E63BPN6hWuT9sK\nHWhR5g38DOqfPZ0T6I9EYJ4yAUP4HgDsTV/DMnIMzspV1A0mhBD/IIWcji7EnWfzmQ18cmYzVxOj\nACjuX5K2FQbQunw7SuYqpXLCnEN3+hTmaZMwfukeYJP8QkMsoWNw1H5K5WRCCHF/UshPKN4ex47z\n29l8egMHb/0GgK+XHx0qdqJtxQ48U6ieTNjKRNqLFzDPnIpx2xY0ikJKnaexjHqflOdeUDuaEEI8\nkBTyY3C4HPwQtYdNpzew+9IX2J12NGh4sWhD2lbsQLNSLTB5mdSOmaNob1zHNHsG3hvWuudNV6mG\nZVQYyY1fkXnTQogsQQr5EZyKPcnmMxvYenYzt623ACiXuzxtK3agVfm2FPYtonLCnEcTE4NpwRx8\nVn2Ixm7HUaYs1pFjsLd4U+ZNCyGyFCnkh4hNimX7uS1sPrORY9FHAMhtzE3Xqt1oW6EDNfPXRiOP\nwDKdJiEenyUL3fOmLYk4ixbDMjwUe+t2Mm9aCJElyW+u+0h2JvPd5W/YdGY9313+GofLgU6j4+US\nTWlbsQMvl3wVo86odsycyWLBZ+VyTIvmoo2LwxWYn3tjxmLr2AWM8m8ihMi6pJD/pCgKx6KPsPnM\nBraf+4Q7tjsAVMlbjbYV29OyXBvym/I/5Cgiw9jteH+8GvOcmWijb+PKnZvEMeNJCu4BZrPa6YQQ\n4onl+EK+ZbnJJ2c3s+XMBk7fOQVAPp9AetboS9sKHaiar5rKCXM4hwPjJ5swz5yK7moULrMvliEh\nJPXuJ/OmhRDZSo4s5CRHErsvfsHmMxsIj9qDS3Fh0BpoXvoN2lXsQMNijfHSeakdM2dzuTDu3IFp\n+mT058+hGI1Ye/XDOmAISr58aqcTQoh0l2MK+f9v6PDZ+U9JSI4HoFb+2rSp2IG3yr5NgHcelVMK\nFAXDd19jnjIR/YnjKHo9SZ26Yh0agquwnMUuhMi+sn0hR927widnNrHlzEYuxEcCUMhcmC5VgmlT\noT3l81RQOaH4i9eB/e550wd/c8+bbtUWy/BQXKVKqx1NCCEyXLYs5L82dPj0yy3svbQXkA0dPJk+\n4iDmKRMx7HP/W9mbtcAyYjTOSpVVTiaEEJkn2xSyoigcuL6fTafX/21Dh7qFnqVdxXdkQwcPpDt5\nwj1vevcXACQ3aIQlNAxHzdoqJxNCiMyXbQp5y5mN9N/TC3Bv6NCmfH96P9sdP4dsOO9ptBciMc+Y\ngvHTre5500/Xdc+bfvY5taMJIYRqsk0h1y38LANrDaVR8capGzoEBshG3J5Ee+0qpjkz8N6wDo3T\nSUq1GlhDx5D80ssyb1oIkeNlm0Iu4V+S0XXHqh1D3IcmOhrTgtn4rF7pnjddrjyWEaNJbv6GzJsW\nQog/ZZtCFp5HEx+Hz5IFmJYtRWO14CxW3D1vulVbmTcthBD/IL8VRfqzWPBZ8QGmRfPRxsfhzF8A\na9h4bB07y7xpIYT4D1LIIv3Y7fis/QjTvNnuedMBASSGTXDPmzbJ/tBCCPEgUsjiyTkceG/egGn2\n9P/Nmx46wj1v2j+X2umEECJLkEIWj8/lwvjZdkwzpqCPPI/i7Y21zwCs/Qej5M2rdjohhMhSpJDF\no1MUDN/sxjx1IvqTf7jnTXcJxjp4OK5ChdVOJ4QQWZIUsngkXvt/wDxlAl6HfnfPm27THsuwkbhK\nllI7mhBCZGlSyCJN9Id+d8+b3h8OgP21193zpitWUjeYEEJkE1LI4sGOHcM/ZCTGr78CILlRY/e8\n6Ro1VQ4mhBDZixSyuC9d5DlMM6bAju0YFYWUZ+phGT2WlLrPqh1NCCGyJSlk8Tfaq1GYZk/He9N6\nNE4n1KpFXMhoUho2lnnTQgiRgaSQBQCa27cxzZ+Fz5qP0CQn4yhfAcuIMeTq+g4pMYlqxxNCiGxP\nCjmH08TdxbR4AT4fLkVjteIsXuJ/86Z1OnlULIQQmUQKOadKTMT04VJ8Fi9AmxCPs0BBrGMnYXvn\nXTAY1E4nhBA5jhRyTmOz4bNmJab5s9HGxLjnTY+dRFLXbjJvWgghVCSFnFOkpOC9ab173vT1a7h8\n/bAMDyWpV18UP3+10wkhRI4nhZzduVwYP93qnjd98YJ73nTfgVj7D0LJI/OmhRDCU0ghZ1eKgmH3\nl5inTUJ/6gSKlxdJXbu5500XLKR2OiGEEP8ghZzdKApe+8IxT52AV8QhFK0WW9sO7nnTJUqqnU4I\nIcR/kELORvS//Yp56gQMB/YDYG/xpnvedPkKKicTQgjxMFLI2YDu+DHM0yZi/PZrAOwvNcEaGoaj\nepDKyYQQQqSVFHIWpjt/DtP0yXh/th2A5Hr1sYS+j6NuPZWTCSGEeFRSyFmQNuoKplnT8N68AY3L\nRUqNmlhGvU9Kg0YyWca2LLgAAAw0SURBVEsIIbIoKeQsRHPrFuZ5M/FeuwpNSgqOChWxjAwjuVlz\nKWIhhMjipJCzAM3dO5gWzcdnxQdokpJwliiJJWQU9pat3fOmhRBCZHlSyB5Mk3gPn2VL/q+9ew+K\n6r6jAH52F1Z2YcVHoL7SV8Ym1leqJg2xqIBVjPiIEFBCrAbRUTQRtaxoNDGJUdSi1SRqba1Wm9GJ\nk7E040xiaplJ6iNNJNb4ABOJOBhEhIhyd9lw+faPrZtHVVZZuD/wfP5i5K6cOaMeL7v7A7bXN8B8\ntQZ6127QXlwBd+pTQHCw0fGIiCiAOMgqcrlg2/Yn2Nf/DubLl9HQuTOuLXsFrinpgM1mdDoiImoG\nHGSVfP01Qt7YAXveKli+vIAGR3vUOhfDNWMWJMxhdDoiImpGHGQV6DravfUmQle9Asu5LyA2G7Q5\nWdBmPwvp2MnodERE1AI4yEYSgXXf2wjNfRlBp095z5tOnw5t7gI0/KCL0emIiKgFcZCNIILgggPe\n86Y/KYSYzXBNSoM234mGH/7I6HRERGQADnILCzp8yHve9KF/AQDcYx+H5lwMvefPDE5GRERG4iC3\nkKD/fAL7ipfQ7h/7AQB1vx4JbeFzqO/b3+BkRESkAg5yM7MUFyE0dzna/X0vAMDz6K9Qu+h51D/8\nS4OTERGRSjjIzcR87guErlmJdm/u8p43/YsBqM1Ziq+HxvCYSyIi+j8c5AAzXyyHPW8VQnZu9543\n3evnqHU+B8+o0RxiIiK6KQ5ygJiqLsO+YR1sW//gPW/6xz9BrXMx6sYn8rxpIiJqFAe5iUxXa7zn\nTW989Zvzpl/OhXvikzxvmoiI/ObXILvdbiQkJGDWrFmIiopCdnY2dF1HREQEVq9eDavVit69e2PA\ngAG+x2zbtg2Wtnxn6HLB9uc/es+brqpCwz334Fr2Crh+kw6EhBidjoiIWhm/Bnnjxo0IDw8HAKxf\nvx6pqakYNWoU8vLysGfPHqSmpiIsLAw7duxo1rBK8HgQ8te/wL52NSzlX6KhfThqc5ZAy5gJhIUZ\nnY6IiFopc2MXfP755/jss88wbNgwAMCRI0cQFxcHAIiJicGhQ4eaNaAydB3tdr+BTo8OgsM5D+aa\nK9CenY+qfx+DlvVbjjERETVJo3fIubm5WLJkCfbu9b6P1uVywWq1AgA6d+6MS5cuAQA8Hg/mz5+P\nsrIyjBw5ElOnTm30i3fsaEdQUPN+Wzsiook/JUkEeOstYOlS4ORJwGoFnnkGppwc2Lt0gT0wMZXW\n5A4JAHsMFPbYdOwwMALd4y0Hee/evXjwwQdx77333vDzIuL7ODs7G2PHjoXJZEJaWhoGDRqEvn37\n3vKLV1drdxDZfxERDly6dPXOHiyC4H++h9AVLyP4WCHEYoH7ycne86Z7/K+PO/29W5EmdUg+7DEw\n2GPTscPAuNMebzXitxzkgoICnD9/HgUFBSgvL4fVaoXdbofb7UZISAguXryIyMhIAMCkSZN8j3vk\nkUdQXFzc6CCrKvjwQdhfeRHWwwcBAO7HE6FlL4J+X0+DkxERUVt1y0Fet26d7+MNGzage/fuKCws\nxDvvvINx48bh3XffRXR0NM6ePYvXXnsNa9asga7rOHr0KOLj45s9fKAFHStE6IqXYD3wHgCgbuQo\n1Dqfg96ndf7HgoiIWo/bfh/ynDlz4HQ6sXv3bnTr1g3jx49HcHAwunTpgqSkJJjNZsTGxqJfv37N\nkbdZWIpOe8+bfvtvAABP9FDU5ixB/aCHDU5GRER3C5N8+4ngFtbcz2M09j1+8xcl3vOm9+z2njc9\ncJD3vOkhw5o1V2vC55sCgz0GBntsOnYYGC3+HHJbZS7/8pvzpuvrUd+rN2oXLYVnRDzPmyYiIkPc\nVYNsunwZ9g1rvedNu92o/+l90JyLUTduAmBu9C3ZREREzeauGGRTzRXYNr4K2+bXYb52FXr3HtAW\nLIQ7JRUIuisqICIixbXtNdI02Dasg/3VtTBXV6Phnghcy3kOrqem8rxpIiJSStscZI8HITu2Ab9f\ng7DycjSEd8C1xc/DlT6DR1wSEZGS2tYg19ej3Z7dCF2zEpbSc0BoKGqzFsA16xlIeAej0xEREd1U\nmxlky5litJ+SiqAzxRCrFdqMWbC/+Dw0k83oaERERI1qM4McdOI4LCVn4XpqCrR52Wjo3gP2CMdd\ncd40ERG1fm1mkOvGJ6JuzHjA0rw/PYqIiKg5tK0333KMiYiolWpbg0xERNRKcZCJiIgUwEEmIiJS\nAAeZiIhIARxkIiIiBXCQiYiIFMBBJiIiUgAHmYiISAEcZCIiIgVwkImIiBTAQSYiIlKASUTE6BBE\nRER3O94hExERKYCDTEREpAAOMhERkQI4yERERArgIBMRESmAg0xERKSAIKMDNNWqVavw8ccfo76+\nHjNmzMCIESMAAO+//z6mTZuGoqIiAMDp06exaNEiAEBcXBwyMzMNy6wif3tcu3Ytjhw5AhHB8OHD\nkZGRYWRspXy/wwMHDuDEiRPo0KEDACA9PR3Dhg1Dfn4+tm/fDrPZjOTkZDzxxBMGJ1eLvz3u27cP\nW7duhdlsRlRUFLKysgxOrhZ/e7xu3rx5sFqtWLlypUGJ1eNvhwHbF2nFDh06JNOmTRMRkaqqKhk6\ndKiIiLjdbklLS5PBgwf7rk1KSpJPP/1UdF2XrKws0TTNiMhK8rfHoqIiSUlJERERXdclPj5eKioq\nDMmsmht16HQ65cCBA9+5rra2VkaMGCE1NTXicrlk9OjRUl1dbURkJfnbo6ZpEhMTI1evXpWGhgZJ\nSkqSM2fOGBFZSf72eN0HH3wgiYmJ4nQ6WzKm0m6nw0DtS6u+Q37ooYfQr18/AED79u3hcrmg6zo2\nbdqE1NRUrF69GgBQWVkJTdPQu3dvAEBeXp5hmVXkb48OhwN1dXXweDzQdR1msxk2m83I6Mq4WYff\nd+zYMfTt2xcOhwMAMGDAABw9ehSxsbEtmldV/vZos9mQn5+PsLAwAECHDh3w1VdftWhWlfnbIwB4\nPB5s3LgRM2fOxP79+1syptL87TCQ+9Kqn0O2WCyw2+0AgD179mDIkCEoLS3F6dOnMWrUKN91ZWVl\nCA8Px8KFCzFx4kRs27bNoMRq8rfHrl27Ij4+HjExMYiJicHEiRN9/yDe7W7UocViwc6dOzF58mRk\nZWWhqqoKlZWV6NSpk+9xnTp1wqVLl4yKrRx/ewTg+7NXVFSEsrIy9O/f37DcqrmdHjdv3oxJkybx\n7/L3+NthQPelSff0iti/f78kJSVJTU2NZGRkyLlz50REJCYmRkRECgsLJTo6WqqqqkTTNBkzZowU\nFxcbGVlJjfVYWloqiYmJomma1NTUyGOPPSaVlZVGRlbOtzs8ePCgnDx5UkRENm/eLMuWLZP8/HxZ\nvny57/q8vDzZtWuXUXGV1ViP15WUlEhCQoLv8/RdjfVYUlIi06dPFxGRw4cP81vWN9BYh4Hcl1Z9\nhwx4X3S0adMmbNmyBZqm4ezZs1iwYAGSk5NRUVGBtLQ0dO7cGT179kTHjh1hs9kwcOBAnDlzxujo\nSvGnx+PHj6N///6w2WxwOBy4//77UVxcbHR0ZXy7Q4fDgaioKPTq1QsAEBsbi+LiYkRGRqKystL3\nmIqKCkRGRhoVWUn+9AgA5eXlyMzMxMqVK32fp2/402NBQQEuXLiA5ORkLFu2DAUFBdiyZYvBydXh\nT4cB3ZdA/k+ipdXU1EhCQsJN79Ku39mJiKSkpEh1dbXoui4pKSly6tSploqpPH97PH78uCQnJ4uu\n6+LxeGT06NFy/vz5loyqrBt1OHv2bCktLRURkZ07d8oLL7wgLpdLhg8fLleuXJFr1675XuBFXv72\nKCLy9NNPy4cffmhITtXdTo/X8Q75u26nw0DtS6t+Ude+fftQXV2NuXPn+n4tNzcX3bp1+79rc3Jy\nkJGRAZPJhOjoaDzwwAMtGVVp/vbYp08fDB48GKmpqQCApKQk9OjRo0WzqupGHU6YMAFz586FzWaD\n3W7HihUrEBISgvnz5yM9PR0mkwmZmZm+F3iR/z2WlJTgo48+wvr1633XTZkyBXFxcUbEVo6/PdLN\n3U6HgdoX/vhFIiIiBbT655CJiIjaAg4yERGRAjjIRERECuAgExERKYCDTEREpAAOMhERkQI4yERE\nRArgIBMRESngvy5pVG+fzySIAAAAAElFTkSuQmCC\n", + "text/plain": [ + "
\n", - "\n", - "You know what's important for understanding Deep Learning / Machine Learning?
\n", - "Intuition. Period.\n", - "\n", - "And Intuition comes when you run the code multiple times.\n", - "\n", - "So, today I can write a couple of defination and say this is this, this is that.
\n", - "You Google half of the things up. You find answers which you need to Google further.
\n", - "In the process, you probably won't even remember what's the first thing you started out with!\n", - "\n", - "So?\n", - "\n", - "Hence on, I will execute cells with code.
\n", - "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n", - "**No Theory Just Code.**\n", - "\n", - "I will at max give a defination that extends for a line. That's it.
\n", - "Let's get started!\n", - "\n", - "
\n", - "\n", - "**RECOMMENDED!**
\n", - "Write the code in the cells using the signals sent by your brain to your fingers!
\n", - "Don't just `shift+enter` the cells.\n", - "\n", - "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)" - ] - }, - { - "metadata": { - "id": "gYWUpE-bYKWP", - "colab_type": "code", - "colab": {} - }, - "cell_type": "code", - "source": [ - "# Essential imports\n", - "import numpy as np\n", - "import tensorflow as tf\n", - "import matplotlib.pyplot as plt" - ], - "execution_count": 0, - "outputs": [] - }, - { - "metadata": { - "id": "eKpz5NCIYMdi", - "colab_type": "code", - "colab": {} - }, - "cell_type": "code", - "source": [ - "# Let's define some tensors\n", - "t1 = tf.constant(2.0, dtype=tf.float32)\n", - "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n", - "t3 = tf.constant([[[1.45, 9.0], [2.0, 3.0], [4.0, 5.0]], \n", - " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])" - ], - "execution_count": 0, - "outputs": [] - }, - { - "metadata": { - "id": "vmMcjzTxbWzw", - "colab_type": "code", - "outputId": "1396b865-0a11-4b31-a1d5-9510e6b20301", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 68 - } - }, - "cell_type": "code", - "source": [ - "# Let's print them out!\n", - "print (t1)\n", - "print (t2)\n", - "print (t3)" - ], - "execution_count": 6, - "outputs": [ - { - "output_type": "stream", - "text": [ - "Tensor(\"Const_3:0\", shape=(), dtype=float32)\n", - "Tensor(\"Const_4:0\", shape=(2,), dtype=float32)\n", - "Tensor(\"Const_5:0\", shape=(2, 3, 2), dtype=float32)\n" - ], - "name": "stdout" - } - ] - }, - { - "metadata": { - "id": "10ahnfjYbcop", - "colab_type": "text" - }, - "cell_type": "markdown", - "source": [ - "Where's Waldo?
\n", - "I mean, the value?
\n", - "\n", - "So, the thing is you can't print the value of tensors directly.
\n", - "You have to use `session`, so let's do that!" - ] - }, - { - "metadata": { - "id": "ol6O5I7Tb2nb", - "colab_type": "code", - "outputId": "1c005d9c-951d-48be-94e5-8681eaefca4d", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 204 - } - }, - "cell_type": "code", - "source": [ - "sess = tf.Session()\n", - "print (sess.run(t1))\n", - "print (\"=======================\")\n", - "print (sess.run(t2))\n", - "print (\"=======================\")\n", - "print (sess.run(t3))\n", - "sess.close()" - ], - "execution_count": 7, - "outputs": [ - { - "output_type": "stream", - "text": [ - "2.0\n", - "=======================\n", - "[1. 2.]\n", - "=======================\n", - "[[[1.45 9. ]\n", - " [2. 3. ]\n", - " [4. 5. ]]\n", - "\n", - " [[1. 9. ]\n", - " [2. 3. ]\n", - " [4. 5. ]]]\n" - ], - "name": "stdout" - } - ] - }, - { - "metadata": { - "id": "rXKfVs_zb-kU", - "colab_type": "text" - }, - "cell_type": "markdown", - "source": [ - "Aaahaa!! Just printed those tensors!!!
\n", - "Feels good!
\n", - "\n", - "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n", - "And you are still using the markdown cells for the theory ?!\n", - "\n", - "I am just gonna say I am a unreasonable man.
\n", - "\n", - "\n", - "So, you are programming with tf.
\n", - "What ever you do is broken down to 2 basic steps:\n", - "- Building the computational Graph!\n", - "- Execute that graph using `session`!\n", - "\n", - "That's all!\n", - "\n", - "
\n", - "\n", - "Let's compare this 2 steps with what we did above!
\n", - "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n", - "And then I executed each tensor in this graph using a `session`.\n", - "\n", - "That simple!\n", - "\n", - "
\n", - "\n", - "Now, let's define a few more computational graphs and execute them with sessions.\n", - "\n", - "Okay, to start with let's build this computational graph!\n", - "\n", - "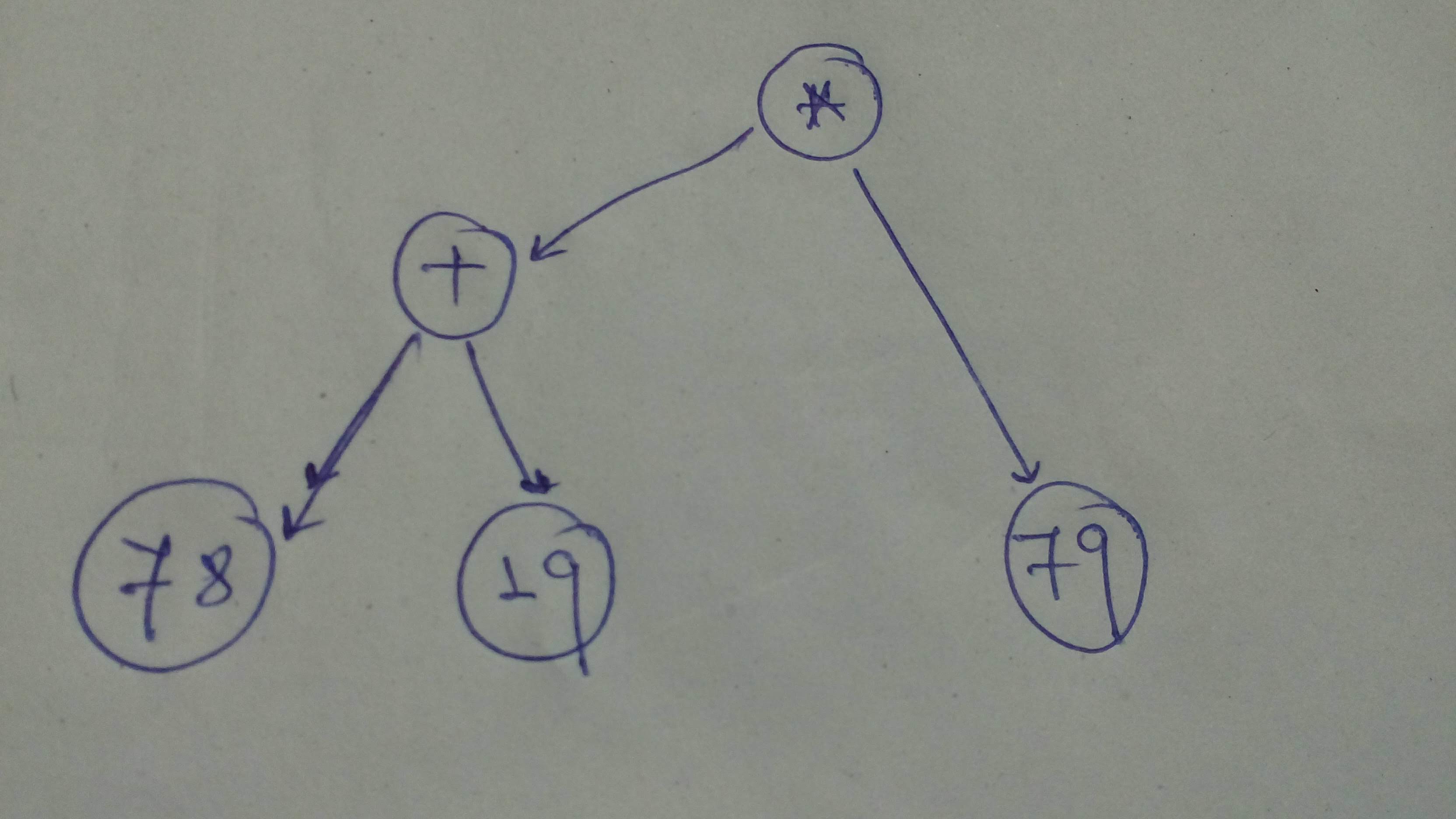" - ] - }, - { - "metadata": { - "id": "FyVz0GNqgreZ", - "colab_type": "code", - "outputId": "e345fccd-ca78-49bf-b9dd-ae0a6d29da9f", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 51 - } - }, - "cell_type": "code", - "source": [ - "# Let's define the graph\n", - "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n", - "\n", - "# Alternatively\n", - "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n", - "\n", - "# Let's execute using session\n", - "sess = tf.Session()\n", - "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n", - "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n", - "sess.close()" - ], - "execution_count": 8, - "outputs": [ - { - "output_type": "stream", - "text": [ - "Comp Graph 1 : 7663\n", - "Comp Graph 1 Alt: 7663\n" - ], - "name": "stdout" - } - ] - }, - { - "metadata": { - "id": "SVMMtuFYhaQB", - "colab_type": "text" - }, - "cell_type": "markdown", - "source": [ - "Let's define a sligtly more involved graph!\n", - "\n", - "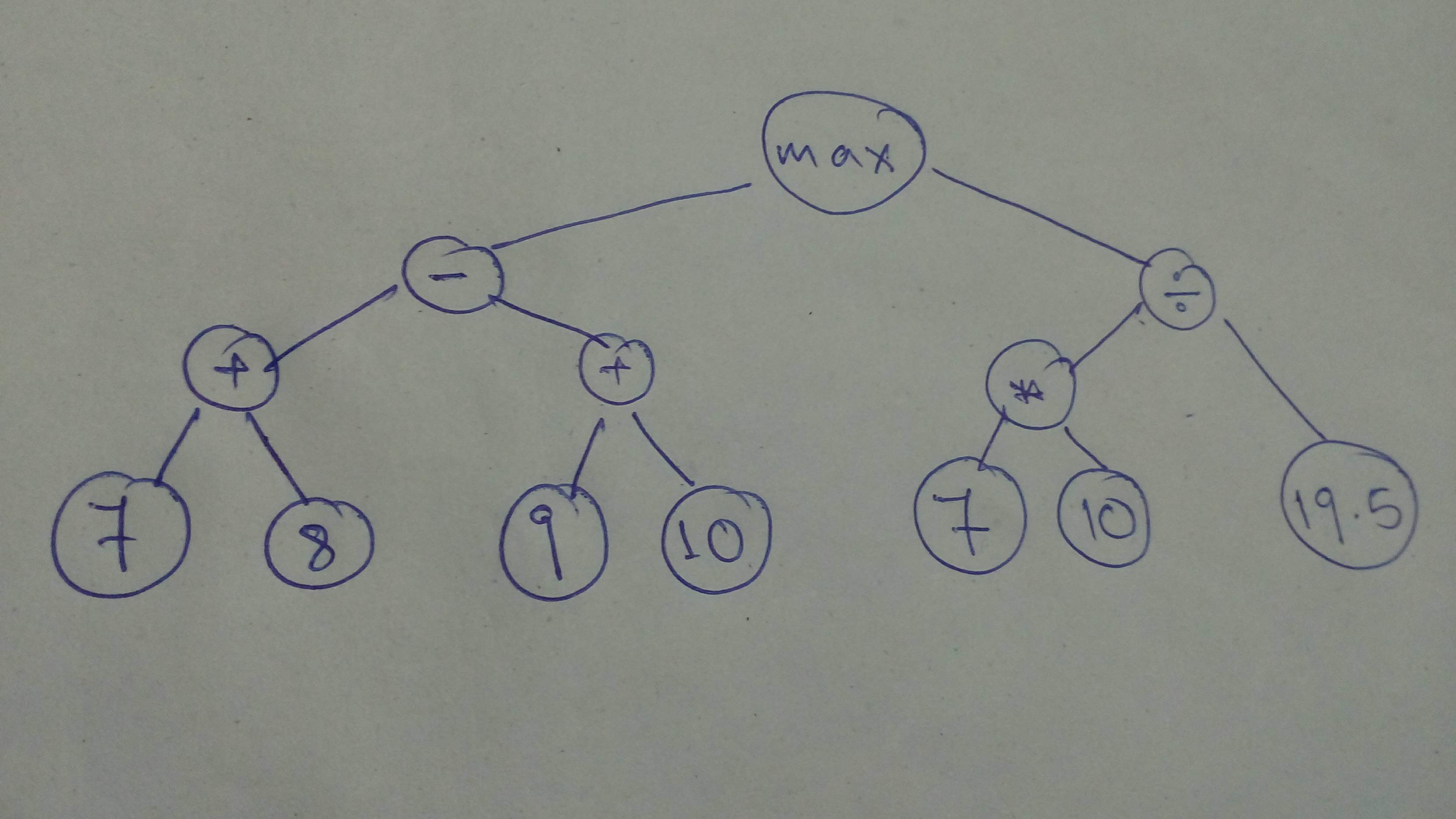" - ] - }, - { - "metadata": { - "id": "4856BTvRhiBb", - "colab_type": "code", - "outputId": "50a23939-418c-4565-bd87-b66b9ee7b2bf", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 68 - } - }, - "cell_type": "code", - "source": [ - "# Let build the graph\n", - "# We need to cast cause the tensors operated on should be of the same type\n", - "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n", - " dtype=tf.float32)\n", - "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n", - "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n", - "\n", - "# Let's execute\n", - "sess = tf.Session()\n", - "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n", - "print ('Complete Result: ', total_res)\n", - "print ('Part 1 Result: ', part1_res)\n", - "print ('Part 2 Result: ', part2_res)\n", - "sess.close()" - ], - "execution_count": 9, - "outputs": [ - { - "output_type": "stream", - "text": [ - "Complete Result: 3.5897436\n", - "Part 1 Result: -4.0\n", - "Part 2 Result: 3.5897436\n" - ], - "name": "stdout" - } - ] - }, - { - "metadata": { - "id": "B-_ZDtEbj4N0", - "colab_type": "text" - }, - "cell_type": "markdown", - "source": [ - "Cool! Let's go! Build another graph and execute it with sessions.
\n", - "\n", - "But this time, it's all you!\n", - "\n", - "Build this graph and execute it with `session`!\n", - "\n", - "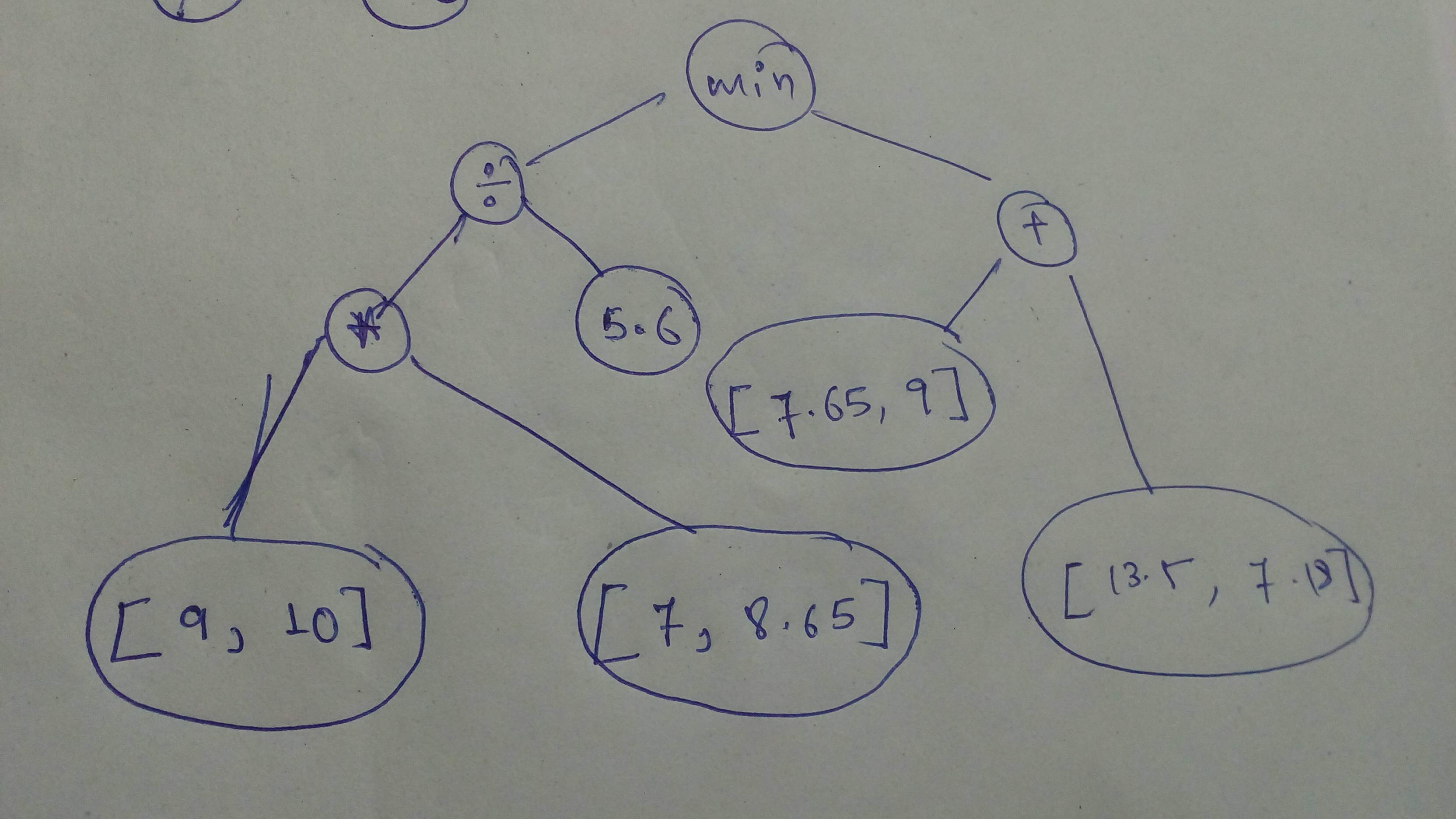\n", - "\n", - "_Remember that `tensors` operated on should be of the same type!_
\n", - "_Search up errors and other help you need on Google_" - ] - }, - { - "metadata": { - "id": "-uHNe1BolJY0", - "colab_type": "code", - "outputId": "25007c20-00d5-4239-ab31-3e319120d77b", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 119 - } - }, - "cell_type": "code", - "source": [ - "# Build the graph\n", - "# YOUR CODE HERE\n", - "node_1 = tf.constant([9, 10], dtype=tf.float32, name='leaf_node1')\n", - "node_2 = tf.constant([7, 8.65], dtype=tf.float32, name='leaf_node2')\n", - "node_3 = tf.constant(5.6, dtype=tf.float32, name='leaf_node3')\n", - "node_4 = tf.constant([7.65, 9], dtype=tf.float32, name='leaf_node4')\n", - "node_5 = tf.constant([13.5, 7.18], dtype=tf.float32, name='leaf_node5')\n", - "\n", - "cg_part_1=(node_1 * node_2)\n", - "\n", - "cg_part_2=(node_4 + node_5)\n", - "\n", - "cg_part_3=tf.divide(cg_part_1, node_3)\n", - "\n", - "comp_graph_2 = tf.minimum(((node_1 * node_2) / node_3),\n", - " (node_4 + node_5))\n", - "\n", - "comp_graph_2_alt=tf.minimum(cg_part_2, cg_part_3)\n", - "# Execute \n", - "# YOUR CODE HERE\n", - "with tf.Session() as sess:\n", - " print(sess.run(comp_graph_2))\n", - " part1, part2, part3, total = sess.run([cg_part_1, cg_part_2, cg_part_3, comp_graph_2_alt])\n", - "print (\"=======================\")\n", - "print ('Part 1 Result: ', part1)\n", - "print ('Part 2 Result: ', part2)\n", - "print ('Part 3 Result: ', part3)\n", - "print ('Final Result: ', total)" - ], - "execution_count": 10, - "outputs": [ - { - "output_type": "stream", - "text": [ - "[11.25 15.446429]\n", - "=======================\n", - "Part 1 Result: [63. 86.5]\n", - "Part 2 Result: [21.15 16.18]\n", - "Part 3 Result: [11.25 15.446429]\n", - "Final Result: [11.25 15.446429]\n" - ], - "name": "stdout" - } - ] - }, - { - "metadata": { - "id": "qmap38WelREN", - "colab_type": "text" - }, - "cell_type": "markdown", - "source": [ - "Let's do another!
\n", - "It's fun! Isn't it?!\n", - "\n", - "Build and execute this one!\n", - "\n", - "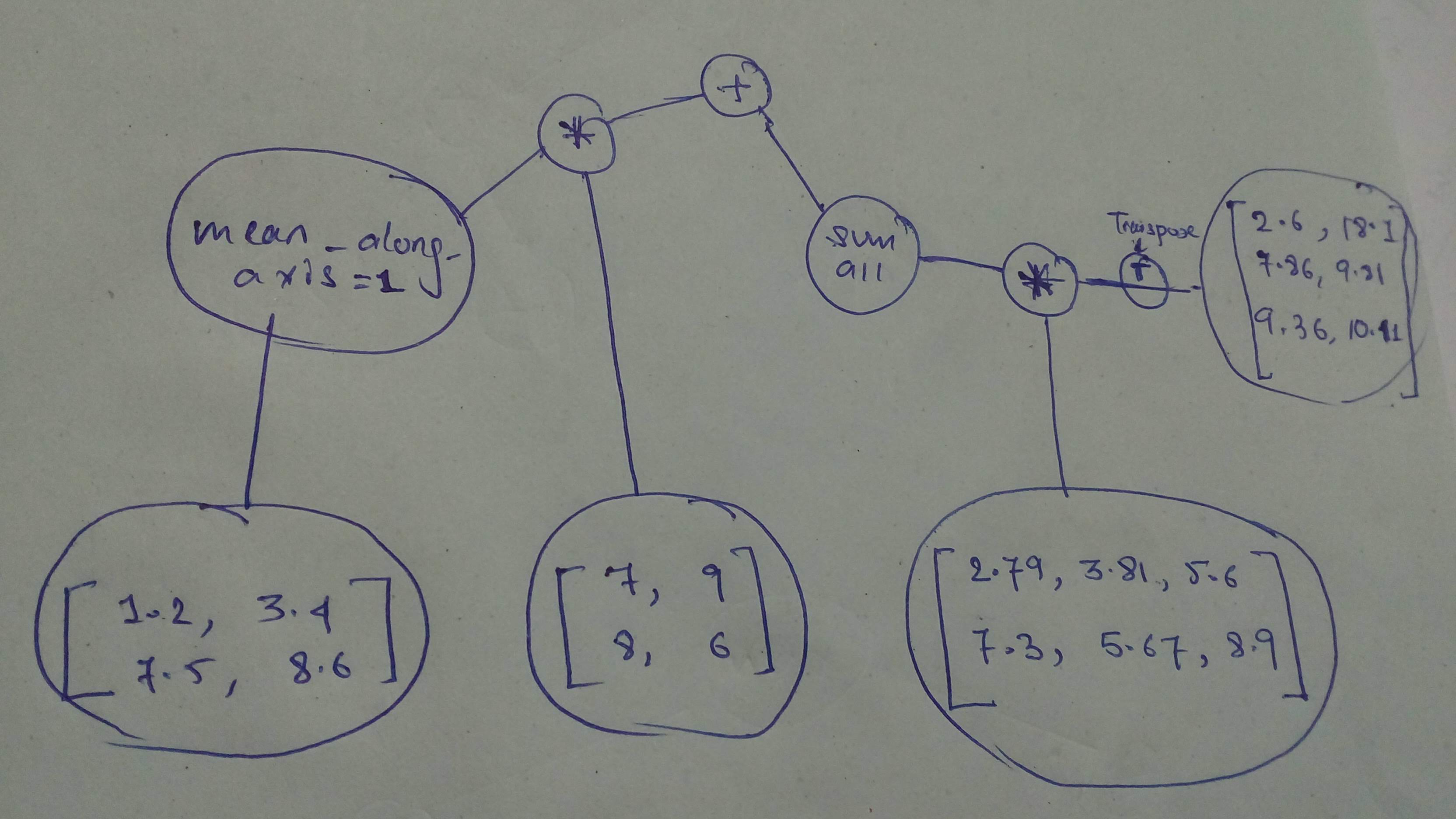" - ] - }, - { - "metadata": { - "id": "0ZhYwAlLmEvB", - "colab_type": "code", - "outputId": "4b97a028-dc5d-4d7b-b640-b21e85c7b8bd", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 238 - } - }, - "cell_type": "code", - "source": [ - "# Build the graph\n", - "# YOUR CODE HERE\n", - "node_6 = tf.constant([[1.2 , 3.4],\n", - " [7.5 , 8.6]], dtype = tf.float32, name='leaf_node6')\n", - "node_7 = tf.constant([[7 , 9],\n", - " [8 , 6]] , dtype = tf.float32, name='leaf_node7')\n", - "node_8 = tf.constant([[2.6 , 18.1],\n", - " [7.86 , 9.81],\n", - " [9.36 , 10.41]] , dtype = tf.float32, name='leaf_node8')\n", - "node_9 = tf.constant([[2.79 , 3.81 , 5.6],\n", - " [7.3 , 5.67 , 8.9]] , dtype = tf.float32, name='leaf_node9')\n", - "\n", - "cg_1 = tf.reduce_mean(node_6, axis = 1)\n", - "cg_2 = tf.transpose(node_8)\n", - "cg_3 = tf.multiply(node_7 , cg_1)\n", - "cg_4 = tf.multiply(node_9 , cg_2)\n", - "cg_5 = tf.reduce_sum(cg_4)\n", - "cg_com = cg_3 + cg_5\n", - "\n", - "#cg_1alt = (node_7 * (np.mean(node_6, axis = 1)))\n", - "#cg_1alt = (node_7 * (tf.reduce_mean(node_6, axis = 1)))\n", - "#cg_2alt = np.sum((node_9 * tf.transpose(node_8)))\n", - "#cg_2alt = tf.reduce_sum((node_9 * tf.transpose(node_8)))\n", - "#cg_comalt = cg_1alt + cg_2alt\n", - "\n", - "# Execute \n", - "# YOUR CODE HERE\n", - "with tf.Session() as sess:\n", - " print(sess.run(cg_com))\n", - " part_1, part_2, part_3, part_4, part_5, final = sess.run(\n", - " [cg_1, cg_2, cg_3, cg_4, cg_5, cg_com])\n", - "print (\"=======================\")\n", - "print ('Part 1 Result: ', part_1)\n", - "print ('Part 2 Result: ', part_2)\n", - "print ('Part 3 Result: ', part_3)\n", - "print ('Part 2 Result: ', part_4)\n", - "print ('Part 3 Result: ', part_5)\n", - "print ('Final Result: ', final)" - ], - "execution_count": 11, - "outputs": [ - { - "output_type": "stream", - "text": [ - "[[386.1183 442.4683 ]\n", - " [388.41827 418.3183 ]]\n", - "=======================\n", - "Part 1 Result: [2.3000002 8.05 ]\n", - "Part 2 Result: [[ 2.6 7.86 9.36]\n", - " [18.1 9.81 10.41]]\n", - "Part 3 Result: [[16.100002 72.450005]\n", - " [18.400002 48.300003]]\n", - "Part 2 Result: [[ 7.2539997 29.9466 52.415997 ]\n", - " [132.13 55.622704 92.648994 ]]\n", - "Part 3 Result: 370.01828\n", - "Final Result: [[386.1183 442.4683 ]\n", - " [388.41827 418.3183 ]]\n" - ], - "name": "stdout" - } - ] - }, - { - "metadata": { - "id": "BnB0b6qCmGmg", - "colab_type": "text" - }, - "cell_type": "markdown", - "source": [ - "And a final one, before we move on to the next part!\n", - "\n", - "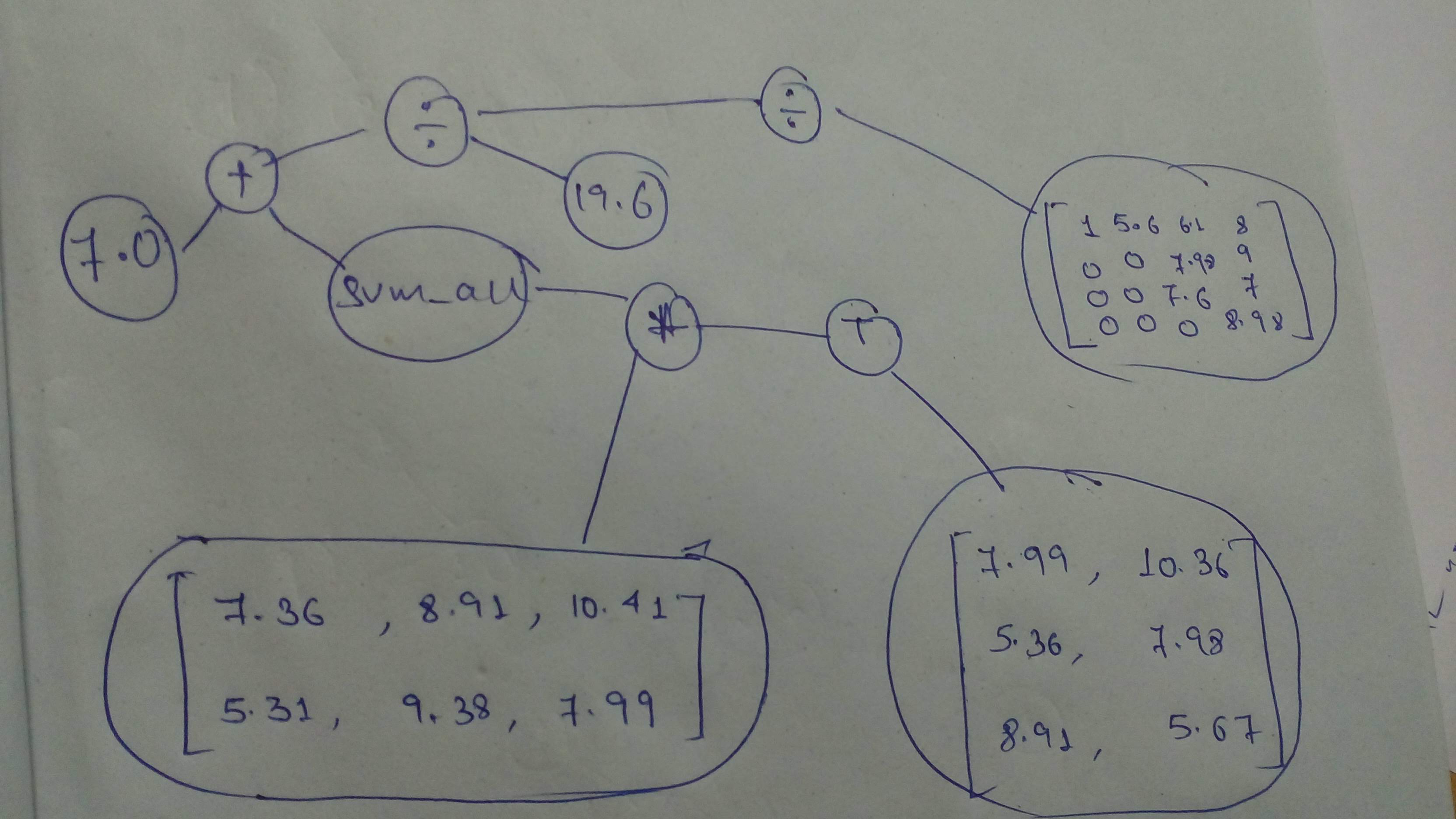" - ] - }, - { - "metadata": { - "id": "GQWyCvsQmMcL", - "colab_type": "code", - "outputId": "69060a80-9d7f-4b1a-b125-683be586a07a", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 357 - } - }, - "cell_type": "code", - "source": [ - "# Build the graph\n", - "# YOUR CODE HERE\n", - "\n", - "node_10 = tf.constant([[7.36 , 8.91 , 10.41],\n", - " [5.31 , 9.38 , 7.99]] , dtype = tf.float32, name='leaf_node10')\n", - "node_11 = tf.constant([[7.99 , 10.36],\n", - " [5.36 , 7.98],\n", - " [8.91 , 5.67]] , dtype = tf.float32, name='leaf_node11')\n", - "node_12 = tf.constant([[1.0 , 5.6 , 6.1 , 8.0],\n", - " [0 , 0 , 7.98 , 9.0],\n", - " [0 , 0 , 7.6 , 7],\n", - " [0 , 0 , 0 , 8.98]] , dtype = tf.float32, name='leaf_node12')\n", - "\n", - "c_graph1 = tf.transpose(node_11)\n", - "c_graph2 = (node_10 * c_graph1)\n", - "c_graph3 = tf.reduce_sum(c_graph2)\n", - "c_graph4 = tf.add(c_graph3 , 7.0)\n", - "c_graph5 = tf.divide(c_graph4 , 19.6)\n", - "c_graph_final = tf.divide(c_graph5 , node_12)\n", - "\n", - "c_graph_alt = (((tf.reduce_sum(node_10 * tf.transpose(node_11))) + 7.0) / 19.6/node_12)\n", - "\n", - "# Execute \n", - "# YOUR CODE HERE\n", - "\n", - "with tf.Session() as sess:\n", - " print(sess.run(c_graph_final))\n", - " pt_1, pt_2, pt_3, pt_4, pt_5, rslt = sess.run(\n", - " [c_graph1, c_graph2, c_graph3, c_graph4, c_graph5, c_graph_final])\n", - "print (\"\\n\\n=======================\\n\\n\")\n", - "print ('Part 1 Result: ', pt_1)\n", - "print ('Part 2 Result: ', pt_2)\n", - "print ('Part 3 Result: ', pt_3)\n", - "print ('Part 2 Result: ', pt_4)\n", - "print ('Part 3 Result: ', pt_5)\n", - "print ('Final Result: ', rslt)" - ], - "execution_count": 12, - "outputs": [ - { - "output_type": "stream", - "text": [ - "[[19.463488 3.475623 3.1907358 2.432936 ]\n", - " [ inf inf 2.4390335 2.1626098]\n", - " [ inf inf 2.5609853 2.7804983]\n", - " [ inf inf inf 2.1674263]]\n", - "\n", - "\n", - "=======================\n", - "\n", - "\n", - "Part 1 Result: [[ 7.99 5.36 8.91]\n", - " [10.36 7.98 5.67]]\n", - "Part 2 Result: [[58.8064 47.7576 92.7531 ]\n", - " [55.011597 74.8524 45.3033 ]]\n", - "Part 3 Result: 374.48438\n", - "Part 2 Result: 381.48438\n", - "Part 3 Result: 19.463488\n", - "Final Result: [[19.463488 3.475623 3.1907358 2.432936 ]\n", - " [ inf inf 2.4390335 2.1626098]\n", - " [ inf inf 2.5609853 2.7804983]\n", - " [ inf inf inf 2.1674263]]\n" - ], - "name": "stdout" - } - ] - }, - { - "metadata": { - "id": "12NC7XTPsJw7", - "colab_type": "text" - }, - "cell_type": "markdown", - "source": [ - "# Linear Regression\n", - "\n", - "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n", - "\n", - "\n", - "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!" - ] - }, - { - "metadata": { - "id": "hW31RZkjtNwI", - "colab_type": "code", - "colab": {} - }, - "cell_type": "code", - "source": [ - "# Create the dataset\n", - "X = np.linspace(-30.0, 300.0, 300)\n", - "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n", - "\n", - "# Divide it into train and test\n", - "train_X = X[:250]\n", - "train_Y = Y[:250]\n", - "\n", - "test_X = X[250:]\n", - "test_Y = Y[250:]" - ], - "execution_count": 0, - "outputs": [] - }, - { - "metadata": { - "id": "LQKy6U33y4lt", - "colab_type": "code", - "colab": {} - }, - "cell_type": "code", - "source": [ - "# Let's define the hyperparameters\n", - "learning_rate = 0.000005\n", - "n_epochs = 1000\n", - "interval = 50" - ], - "execution_count": 0, - "outputs": [] - }, - { - "metadata": { - "id": "1h1-D8K1uT48", - "colab_type": "code", - "outputId": "2189ad35-c490-4fe6-b530-27517fff8cc8", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 347 - } - }, - "cell_type": "code", - "source": [ - "# let's viz the first 10 datapoints of the dataset\n", - "plt.plot(train_X[:10], train_Y[:10], 'g')\n", - "plt.show()" - ], - "execution_count": 15, - "outputs": [ - { - "output_type": "display_data", - "data": { - "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAFKCAYAAADMuCxnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3XdcVfX/B/AXG9lDxIkKrhzg1lCc\nqWnODKMcIU4scouiYVo4cmKKA2dqkpiVq8SJI8QtLtyGoCLInhfuPb8/+sYjf4kDLnzOvff1/AsP\nl3tfvh+X++JsPUmSJBAREZFQ+qIDEBEREQuZiIhIFljIREREMsBCJiIikgEWMhERkQywkImIiGTA\nUOSLJyVlqv05bW3NkJqao/bn1SWcoXpwjurBOZYeZ6ge6pqjg4PlS5dr3RqyoaGB6AgajzNUD85R\nPTjH0uMM1aOs56h1hUxERKSJWMhEREQywEImIiKSARYyERGRDLCQiYiIZKBUhZycnIxWrVohOjoa\nABAbGwsvLy94eXlh9uzZaglIRESkC0pVyN999x1q1KhR9O+goCAEBAQgLCwMWVlZiIyMLHVAIiIi\nXVDiQo6KioK5uTnq1asHAFAoFEhISICrqysAoHPnzoiKilJPSiIiIi1XokJWKBRYtWoVJk6cWLQs\nNTUVVlZWRf+2t7dHUlJS6RMSERHpgNdeOjM8PBzh4eEvLOvQoQM8PT1fKOD/T5Kk1764ra1ZmVz5\npLjLktGb4wzVg3NUD86x9DhD9SjLOb62kD09PeHp6fnCMi8vL6hUKmzfvh1xcXGIiYnB0qVLkZaW\nVvSYxMREVKpU6ZXPXRbXVnVwsCyTa2TrEs5QPThH9eAcS48zLJmM/HT8/mA/BtYbBEN9Q7XNsbhS\nL9HNJcLCwoq+nj59OgYMGIAGDRrA2dkZ58+fR8uWLREREYGhQ4eWLC0REZFASpUSPgeH4UT8MdS1\nrYfmji3L/DXVerengIAABAYGQqVSwc3NDe7u7up8eiIionKx7MIinIg/hm41e6Bppebl8pp60pvs\n7C0jZbEJhZtmSo8zVA/OUT04x9LjDN/OyfhIfLSnL6paVMORQSdhZ2oPQH1z1JnbLxIREZVUYvZT\njD00Agb6BgjtvrmojMuDWjdZExERaapCVSHGHhqBpNxnmNtuHlpWbl2ur881ZCIiIgCLz83H6ccn\n0bN2b4xx/bzcX5+FTEREOu9o3GEsu7AYTla1ENx5FfT09Mo9AwuZiIh02uOsBHx+eBSM9I2wvvtm\n2JjaCsnBfchERKSzClWFGHPIB8/znmO+x6JyO8XpZbiGTEREOmt+9DeIfhKFvi4D4NN4tNAsLGQi\nItJJEQ9/x/eXlqG2tTOWdf5eyH7jf2MhExGRzonPfAS/I2NhYmCC9T1+gKVx8TdLKi/ch0xERDpF\noVRgVIQ3UvNTsbhjMJpUdBUdCQDXkImISMd8c2Y2LiSew4d1PTG0obfoOEVYyEREpDMO3N+HtVdW\noY5NXSzuFCx8v/G/sZCJiEgnPEx/gC+P+qKCYQWs7/EDLIwsREd6AfchExGR1stX5mNUhDcyFOkI\n7hyChvaNREf6D64hExGR1vv6z5m4knQJH9f/FJ+8M0R0nJdiIRMRkVbbc/cXbLi6Dg3s3sGCDktE\nxykWC5mIiLTW/bS7mHDsC5gZmmN99x9gbmQuOlKxuA+ZiIi0Ul5hHkZGeCOrIBOruq5DPbv6oiO9\nEteQiYhIK806NR3XkmMwtKE3POt7iY7zWixkIiLSOj/f3okfbmxEI/sm+Lb9QtFx3ggLmYiItMqd\n1NuYfHw8zI0ssL7HZlQwrCA60hvhPmQiItIaOQU5GHlwGHIKs7Gu2ya42NQVHemNcQ2ZiIi0xoyT\nU3Az5QaGNx6J/nUHio7zVljIRESkFcJit2NH7Da4OjTF3HbzRcd5ayxkIiLSeDef34D/iUmwMrbG\n+u5bYGJgIjrSW+M+ZCIi0mhZBVkYeXAYcgtzEfL+etSyri06UolwDZmIiDSWJEmYenwC7qTdxmhX\nX3zg3Ed0pBJjIRMRkcbadnMLfr6zE80rtUDgu9+IjlMqLGQiItJI15KvIuDkVNiY2CC0xxYYGxiL\njlQq3IdMREQaJ1ORgZEHhyFfmY/1PX5ADUsn0ZFKjWvIRESkUSRJwqRjX+J++j183nQ8etTqKTqS\nWrCQiYhIo2y6vh6/3duNVpXbIKBNoOg4asNCJiIijXHl2SUEnpoBO1M7hHbfDCMDI9GR1IaFTERE\nGiE9Pw0jIj6DQqVAyHuhqGpRTXQktWIhExGR7EmShPFHP0dcxkNMaD4FXZy6iY6kdixkIiKSvdCY\n1TjwYC/cq7bHtNYBouOUCRYyERHJ2oXEc/g6ahYqVnDA2m4bYaivnWfsspCJiEi2UvNSMOqgN5Qq\nJdZ02wBH88qiI5UZFjIREcmSSlLB78hYxGc9wpRW09GheifRkcoUC5mIiGQp5PL3iPjrD3So3hmT\nWkwTHafMsZCJiEh2op+cQdCZr1HJzBEh74XCQN9AdKQyx0ImIiJZSc5NxugIb0iQsK7bJlQyqyQ6\nUrlgIRMRkWyoJBU+PzwKT7IfY3rrWXCv1l50pHLDQiYiItlYcXEpjj06gi5O7+HL5pNExylXLGQi\nIpKF0wknseDst6hiXhWruoZCX0+3Kkq3/rdERCRLz3KeYcwhH+hBD+u6b4Z9BXvRkcodC5mIiIRS\nqpTwPTwSz3ISMbPt12hTpa3oSEKwkImISKgl5xfiZPxx9KjVE+Oa+omOIwwLmYiIhIl8dAxLzi9E\nDUsnrOiyWuf2G/+b7v7PiYhIqKfZT+B7eCQM9Q2xrvsm2JraiY4klHbeMoOIiGStUFWIMYd8kJyb\nhG/bLUALx1aiIwnHNWQiIip3352dh6jHp/GBc1+McvUVHUcWWMhERFSujvwVgeUXF8PJqhaWd14J\nPT090ZFkgYVMRETlJiEzHp8fGQ1jfWNs6L4F1iY2oiPJBvchExFRuShQFmD0oeFIyUvBgg5L4Fap\nmehIslKqQk5OTkbPnj2xcuVKtGnTBkOHDkVOTg7MzMwAAP7+/mjcuLFaghIRkWabFz0X555Go3+d\nDzG80UjRcWSnVIX83XffoUaNGi8smz9/PurVq1eqUEREpD2yC7IRGrMaqy4Hw9naBUs6reB+45co\ncSFHRUXB3Nyc5UtERC+VpcjExmuhWH35ezzPew5rExus7/EDLI2tREeTpRIVskKhwKpVqxASEoJ5\n8+a98L0VK1YgNTUVLi4uCAgIgKmpqVqCEhGRZsjIT8f6q2ux9soqpOanwsrYGlNaTsco17E6f/GP\nV3ltIYeHhyM8PPyFZR06dICnpyesrF78K2fYsGGoX78+nJycMHv2bGzfvh0jRowo9rltbc1gaGhQ\nwujFc3CwVPtz6hrOUD04R/XgHEuvPGaYmpuK4OhgLD+zHOn56bA1tcU3nb+BX2s/WJtal/nrl4ey\nnKOeJEnS2/6Ql5cXVCoVACAuLg52dnYIDg5G3bp1ix4TGRmJAwcOYOHChcU+T1JSZgkiv5qDg2WZ\nPK8u4QzVg3NUD86x9Mp6hil5z7H2yiqExqxFVkEm7E3t4dvUDz6NR8HCWHv+mFLXHIsr9RJtsg4L\nCyv6evr06RgwYADq1KkDb29vrFixAlZWVoiOjn6hoImISLsk5SRh9ZXvsfFqKHIKs1GxggMmt/TH\nZ419YGFkITqexlHbech6enoYNGgQvL29UaFCBTg6OsLPT3dvo0VEpK0ScxKx6lIwtlzfgNzCXDia\nVUZAm68wpKE3zIzMRMfTWCXaZK0u3GQtT5yhenCO6sE5lp66Zvgk6zFWXlqOrTc2I0+Zh6rm1eDX\nfCIGvzMMpobafwCvLDdZExGR7ojPfITvLy3D9hs/QKFSoLpFDYxvMRleDQbDxMBEdDytwUImIqKX\n+ivjIVZcXIaw2G0oUBWgplUtTGg+BZ71vWBsYCw6ntZhIRMR0Qvup99D8IUl2HlrB5SSEs7WLpjY\nYioG1hsEQ33WRlnhZImICABwN/UOll9cjJ9v74RSUqKuTT1MajkN/esMhIG++q8ZQS9iIRMR6bhb\nKbFYduE7/Hp3N1SSCu/YNcSkltPQ27kfi7gcsZCJiHTU9eRrWHZhEfbe+xUSJDSyb4LJLf3Ry7k3\n9PX0RcfTOSxkIiIdczXpCpac/w4HHuwFALg5NMPklv7oUasn78IkEAuZiEhHXEq8gKUXvsPBh78D\nAFo4tsSUltPRxakbi1gGWMhERFou6lEUvjo8G0fiDgEAWlduiymtpqNj9c4sYhlhIRMRaakzj//E\n4vMLcSL+GACgXVUPTG7lj3ZVPVjEMsRCJiLSIpIk4fTjk1hybiFOPz4JAHjP+T34uU7Gu1XbCU5H\nr8JCJiLSApIkITL+GJacX4joJ1EAgK5O3TCp5TT0avIerweuAVjIREQaTJIkHI07hMXnF+JC4jkA\nQI9aPTGpxTQ0c2whOB29DRYyEZEGkiQJEX/9gSXnFuBy0iUAQK/afTCp5VS4OjQVnI5KgoVMRKRh\njsYdwrdn5uBacgz0oIe+LgMwscVUNKrYWHQ0KgUWMhGRhniY/gCBp2fgj4cHoK+njw/rfoQJLaai\ngd07oqORGrCQiYhkLrcwF99fXIbvLy1DvjIf7lXbY57HIjS0byQ6GqkRC5mISKYkScLvD/Yj8PQM\nxGX+hcrmVTDHPQj96wzkecRaiIVMRCRDd1PvYOapaTj26AiM9I3g12wiJracCgsjC9HRqIywkImI\nZCSrIAvLzi/CmisrUaAqQKcaXTCv/SLUsa0rOhqVMRYyEZEMSJKEX+/+jK//nIUn2Y9Rw9IJc9vN\nR6/avbl5WkewkImIBLv5/AZmnJyCPx+fgomBCSa39Idfs4kwMzITHY3KEQuZiEiQ9Pw0LDo3Hxuu\nroNSUuL9Wr0wt9181LKuLToaCcBCJiIqZypJhZ23dmBuVCCSc5NQ29oZQe0X4r2aPURHI4FYyERE\n5Sgm6TKmn5iC84lnYWZohpltZmNs0y9gYmAiOhoJxkImIioHKXnPMT/6W/xwfSMkSOjn8iG+dv8W\n1Syri45GMsFCJiIqQ0qVEttubsG8M3OQmp+Kerb1Mc9jETpU7yQ6GskMC5mIqIycexqNGSenIibp\nMiyMLDHHfR5GNhkDIwMj0dFIhljIRERq9iznGb49MxthsdsBAJ71vBD47lw4mlcWnIzkjIVMRKQm\nhapCbLoWioVn5yFDkY5G9k0wv8NitK3yruhopAFYyEREavBnwinMODkFN1NuwNrEBgs6LMGwhsNh\nqM+PWXozfKcQEZXCk6zHmBM1C7vv7IIe9DDknc8Q0HY2KlaoKDoaaRgWMhFRCSiUCqyNCcGScwuR\nU5iNZpWaY77HYjR3bCk6GmkoFjIR0Vs6FncEM09Nw920O7A3tUdQ+4X45J0h0NfTFx2NNBgLmYjo\nDT3KjEPg6QDsv78H+nr6GNFkNPxbzYSNqa3oaKQFWMhERK+RV5iHVZeDEXxhCfKUeWhT5V3M91iM\nxhWbiI5GWoSFTERUDEmSEPHXH5h1yh9/ZTxEJTNHLHl3BT6q9zHvUUxqx0ImInqJ+2l3MevUdByO\ni4ChviF83fwwpZU/LI2tREcjLcVCJiL6l+yCbARfWIKQyyugUCngUa0j5nksQn27BqKjkZZjIRMR\n4e/N03vv/YrA0wF4nJ2AahbVMbfdPPR27sfN01QuWMhEpPNupcQi4NQ0nIw/DmN9Y0xoPgXjW0yG\nuZG56GikQ1jIRKSzsguysfjcAqyNWYVCVSG6OnVDUPuFcLapIzoa6SAWMhHppD8eHEDAyamIz3oE\nJ6taCGq/EN1rvs/N0yQMC5mIdEpCZjwCTk3D7w/2wUjfCBOaT8GEFlNgZmQmOhrpOBYyEemEQlUh\n1l9dg4Vn5yG7IAttq7hjUcflPHqaZIOFTERa72LieUyJnIBryTGwNbFFUOdV8GowmNeeJllhIROR\n1srIT0dQ9BxsvrYBEiR4NRiM2e9+C/sK9qKjEf0HC5mItI4kSfjt7m7MOj0dz3ISUdemHhZ1XA73\nau1FRyMqFguZiLTKg/T7mH5iMo49OgITAxNMbz0LnzcbDxMDE9HRiF6JhUxEWkGhVGDVpWAsu7AI\neco8dKrRBQs6LIGztYvoaERvhIVMRBov6vFpTI2cgNupt+BQoRKC24egf52BPKeYNAoLmYg01vPc\n55gb9RV2xG6DHvQwvPFIBLQJhLWJjehoRG+NhUxEGkeSJITFbsecqFlIyUtBI/smWNxpOVo4thId\njajEWMhEpFFup9zC1BMTEPX4NMwMzTHHfR5GuY6FoT4/zkiz8R1MRBohtzAXyy8swspLwShQFaBn\n7d4Iar8Q1S1riI5GpBYlKuTdu3cjODgYTk5OAAB3d3f4+voiNjYWX3/9NQCgfv36mDNnjtqCEpHu\nOhp3GP4nJuGvjIeoZlEd8z0W4/3avUTHIlKrEq8h9+rVC/7+/i8sCwoKQkBAAFxdXTF58mRERkai\nY8eOpQ5JRLopMfsp/CJH4afrP8FAzwC+bn6Y2noGLIwsREcjUju1bbJWKBRISEiAq6srAKBz586I\niopiIRPRW1OqlNhyYyOCzsxBpiIDLRxbYlHHYDSu2ER0NKIyU+JCPnv2LEaMGIHCwkL4+/vD3t4e\nVlZWRd+3t7dHUlKSWkISke64mhyDqcfH4+KzC7AytsbqD1ZjgNMnvBEEab3XFnJ4eDjCw8NfWPbB\nBx/Az88PnTp1wqVLl+Dv74/169e/8BhJkl774ra2ZjA0NHjLyK/n4GCp9ufUNZyhenCOby5LkYXA\nY4EIjg6GSlLhk8afYGmPpahsUVl0NK3A96J6lOUcX1vInp6e8PT0LPb7zZo1Q0pKCmxtbZGWlla0\nPDExEZUqVXrlc6em5rxF1Dfj4GCJpKRMtT+vLuEM1YNzfHMH7u9DwMmpeJydgFpWtbGww1J0duoK\n5AKwAOdYSnwvqoe65lhcqZdoG1BoaCj27dsHALh9+zbs7OxgbGwMZ2dnnD9/HgAQEREBDw+PEsYl\nIl0Qn/kIww54wfuPT5GU+wyTWk5DpNeZv8uYSMeUaB9ynz59MHXqVISFhaGwsBBBQUEAgICAAAQG\nBkKlUsHNzQ3u7u5qDUtE2qFAWYB1Maux6Nw85BTmwL1qeyzquBx1beuJjkYkTIkKuXLlyti6det/\nltepUwc//vhjqUMRkfY6//QspkROwI3n12Bvao8FHZbg4/qf8kYQpPN4pS4iKhfp+Wn49swc/HB9\nIyRI+LTBUAS6z4Wdqb3oaESywEImojIlSRJ+ubsLX52agaTcZ6hv2wCLOi5H26rcpUX0byxkIioz\n99PvwT9yEiLjj8HUwBQz28yGb1M/GBsYi45GJDssZCJSu3xlPlZeWo7lFxYjX5mPLk7vYYHHEtSy\nri06GpFssZCJSK1OJ5zE1MgJuJt2B45mlRHUfiH6uPTnQVtEr8FCJiK1yC7IxlenpmPbzS3Qgx5G\nNBmNGa2/gpWJtehoRBqBhUxEpXbj+XWMjvDG7dRbaGTfBEs7rUAzxxaiYxFpFBYyEZWYJEnYemMz\nZp3yR54yD2Ncx2HWu3NgYmAiOhqRxmEhE1GJZOSnY/Lx8fjt3m7YmNhgXffNeL92L9GxiDQWC5mI\n3trlZxcxKsIbf2U8ROvKbbGm2wZUt6whOhaRRuMNRonojUmShDVXVuKD3d0Ql/EXJjSfgl/7H2AZ\nE6kB15CJ6I2k5D3H+KPjcPDh76hYwQEh74WiU40uomMRaQ0WMhG91pknURgb4YPH2QnwqN4JIe+F\nwtHMUXQsIq3CQiaiYilVSqy4uBTfnZsHCRJmtP4KXzafBAN9A9HRiLQOC5mIXioxJxGfHx6NE/HH\nUNW8GtZ034i2Vd4VHYtIa7GQieg/jj86inGHRyE5Nwnda76PFV1X8zaJRGWMhUxERQpVhfju7DwE\nX1wCQ31DfNNuPka7juN1qInKAQuZiAAACZnxGHPIB2efnkFNq1oI7b4ZTSs1Fx2LSGewkIkIfzw4\ngPFHfZGan4p+Lh9iSadg3hSCqJyxkIl0WL4yH99EBWJdzGqYGphiccdgDG3ozU3URAKwkIl01P30\nexgT4YMrSZdQ16YeQntsQUP7RqJjEeksFjKRDvrlzi5MPj4eWQWZ+KTBEMzzWARzI3PRsYh0GguZ\nSIfkFORg1il/bLu5BWaG5ljVdR0863uJjkVEYCET6YxbKbEYFfEZYlNuonFFV4R23wQXm7qiYxHR\n//BuT0RaTpIk/HhzK7rv6ojYlJsY0WQ0Dnx4mGVMJDNcQybSYlmKTEyJnIDdd8JhbWKDVV1D0dul\nr+hYRPQSLGQiLRWTdBmjIrzxIP0+Wji2wtpuG+FkVVN0LCIqBjdZE2kZSZKwPmYNev38Hh6k38cX\nzSZgT/8/WMZEMsc1ZCItkpaXivHHPsfvD/ahYoWKWNl1Lbo4dRMdi4jeAAuZSEucexqNMRE+iM96\nhHZVPbC623pUNq8iOhYRvSEWMpGGU0kqrLwUjPnRcyFBwrRWAZjYYioM9A1ERyOit8BCJtJgSTlJ\n+OLIaBx7dASVzatgzXsb4F6tvehYRFQCLGQiDXUyPhK+h0fiWU4iujp1w/dd16JihYqiYxFRCbGQ\niTRMoaoQi88vwLLzi2Cgb4DZ734L36ZfQF+PJ00QaTIWMpEGeZL1GGMPj0DU49NwsqyJtd03ooVj\nK9GxiEgNWMhEGuLQwz/gd3QsUvJS0Nu5H5Z1/h7WJjaiYxGRmrCQiWROoVQg6MwcrL7yPUwMTLCg\nwxIMbzQSenp6oqMRkRqxkIlk7K+MhxgTMRwXn12Ai00drOu+GU0quoqORURlgIVMJEOFqkLsuv0T\nZp2ajgxFOjzreWFhx6WwMLIQHY2IyggLmUhGUvNSsPXGFmy6FoqErHiYGZphRZfV8GowWHQ0Iipj\nLGQiGbidcguhV9dg560fkVuYCzNDc4xsMgZj3D5HTataouMRUTlgIRMJIkkSjj06gnUxITgadxgA\nUMPSCSObjMWn7wzhEdREOoaFTFTOcgpyEH47DKExq3E79RYAoG0Vd4x2HYf3a/eCoT5/LYl0EX/z\nicpJQmY8Nl4LxdYbm5CWnwYjfSMMqv8JRrv6wtWhqeh4RCQYC5mojJ1/ehbrYkKw995vUEpKVKxQ\nEZNb+sO78Ug4mjmKjkdEMsFCJioDBcoChF0Lw+JTS3Ah8TwAoKF9Y4xxHYcBdT+CqaGp4IREJDcs\nZCI1Ssl7jm03tmDD1XV4kv0YetDD+7V6YbTbOLSr6sGraxFRsVjIRGpwKyUW62JWY9ftMOQW5sLc\nyALj24zHp3WGo7a1s+h4RKQBWMhEJaSSVDgWdxhrY0Jw/NFRAICTVS2MajIGnzQYApfq1ZGUlCk4\nJRFpChYy0VvKLsjGzls7EBqzGnfT7gAA3Ku2x2jXcehRqycM9A0EJyQiTcRCJnpD8ZmP/nfa0mak\n56fBWN8YXg0GY5SrL2/4QESlxkImegVJknDuf6ct7b+/53+nLTlgaqsZ+KzRCFQyqyQ6IhFpCRYy\n0UsolArsvfcr1sWE4NKziwCAxhVdMdrVFwPqfgQTAxPBCYlI27CQif7lee5zbL2xCRuvheJp9hPo\nQQ89a/fGGNdxeLdqO562RERlhoVMBODm8xsIjVmNXbd/Qp4yDxZGlhjj9jlGNB6NWta1RccjIh3A\nQiadpZJUOPJXBNbGrMaJ+GMAgJpWtTDa1RdeDQbD0thKcEIi0iUlKuTdu3cjODgYTk5OAAB3d3f4\n+vpi6NChyMnJgZmZGQDA398fjRs3Vl9aIjXIKsjCT7E/IjRmNe6n3wMAtK/WAaNdx6FbzR48bYmI\nhCjxGnKvXr3g7+//n+Xz589HvXr1ShWKqCw8yozDhqvrsO3GFmQo0mGsb4xPGgzBKFdfNK7YRHQ8\nItJx3GRNWk2SJJx+fBIbr4biwIO9UEkqOFSoBP/WMzGsoQ8czBxERyQiAgDoSZIkve0P7d69G9u3\nb4eNjQ0KCwvh7++Phg0bYujQobC2tkZqaipcXFwQEBAAU9Pi72pTWKiEoSE3D5L6ZeRn4IcrPyDk\nXAhuJt8EADSr3AwT207EoEaDYGLI05aISF5eW8jh4eEIDw9/YdkHH3yAmjVrolOnTrh06RICAwOx\nd+9eHDp0CPXr14eTkxNmz54NJycnjBgxotjnLovr/Do4WPL6waWkyTO8+fwGNl4LRfitMOQUZsNY\n3xh9XPpjeONRaFW5dbmetqTJc5QTzrH0OEP1UNccHRwsX7r8tZusPT094enpWez3mzVrhpSUFCiV\nSnTr1q1oeZcuXXDgwIESRCV6OwqlAgfu78Wm6+sR9fg0AKCaRXVMaDQZg9/5jJuliUgjlGgfcmho\nKKpUqYLevXvj9u3bsLOzg76+Pry9vbFixQpYWVkhOjoadevWVXdeoiJPsh7jhxubsPXGZjzLSQQA\ndKzeGT5NRqNbzR4w1OchEkSkOUr0idWnTx9MnToVYWFhKCwsRFBQEPT09DBo0CB4e3ujQoUKcHR0\nhJ+fn7rzko7790Favz/YB6WkhJWxNca4joN34xFwseEfgUSkmUp0UJe6cB+yPMlxhpmKDOy8tQOb\nrq3H7dRbAP6+trRP41EYUPcjmBuZC074X3KcoybiHEuPM1QP4fuQiUT6/wdpGekb4cO6nvBpPLrc\nD9IiIipLLGSSHR6kRUS6iIVMssGDtIhIl/ETjoTiQVpERH9jIZMQLztIq5F9E/g0GYUP63rK8iAt\nIqKyxEKmcsWDtIiIXo6FTGWOB2kREb0eC5nKDA/SIiJ6c/xEJLXiQVpERCXDQia14EFaRESlw0Km\nUuFBWkRE6sFCprfGg7SIiNSPhUxvRKlSIurJaey5+wv23d+D5NwkAH8fpDW88Sh0r/U+D9IiIioF\nfoJSsZQqJc48+RO/3d2N/ff3Iin3GQDA3tQeo1194d1oJOrY8iAtIiJ1YCHTC5QqJY4/PI4fLmzH\nvnt7XijhYQ190LdOf7hXbc+1YSIiNeOnKkGpUiL6SRR+u7f7PyU8tOFw9KszgCVMRFTG+Amro/4p\n4T33/t4n/M+FO+xM7TC6+WjN89ziAAAN20lEQVR0q/YB2lXzYAkTEZUTftrqkFeV8NCG3ujrMgDt\nqnmgiqMtkpIyBaclItItLGQtp1QpcfbpGey59wv23vvtPyXcx6U/2lfrwDVhIiLB+Cmshf5dwvvu\n7UFizlMAf5fwkHc+Q986A9CuqgeMDIwEJyUion+wkLWESlLh7JMzRQdm/f8S/mdNmCVMRCRPLGQN\n9k8J/7M5+p8StjWxZQkTEWkYFrKGUUkqnH0ajT13d2Pf/T14mv0EwN8lPPidYejj0h8e1TqyhImI\nNAwLWQP8U8J77/6Cvfd/KyphGxMbljARkZZgIcuUSlLh3NOz2HN3939K+NMGQ9G3zgCWMBGRFmEh\ny8g/Jbz3f/uEn2Q/BvDvEu4Pj2qdWMJERFqIhSzYq0r4kwZD0K/OALSv1hHGBsaCkxIRUVliIQt0\nN/UOPt3/ER5mPAAAWP+vhPu69IdH9U4sYSIiHcJCFiQ+8xE89/ZDQlY8Pqr3MQbW9WQJExHpMBay\nAEk5SUVlPKvt1/iy+STRkYiISDB90QF0TXp+Gj7eNwD30u7ii2YTWMZERASAhVyucgpyMHj/IFxL\njsHQhsPxVds5oiMREZFMsJDLiUKpgM/BITj79Az61/kQ33VYCj09PdGxiIhIJljI5UCpUmLc4VE4\nGncYXZ26YWXXdTDQNxAdi4iIZISFXMYkScLUyAnYc+8XtK3ijg09tvJIaiIi+g8WchmSJAlzor7C\ntptb0KSiG7b1+glmRmaiYxERkQyxkMtQ8MUlCLm8AnVs6uKnPr/AysRadCQiIpIpFnIZ2XRtPeZF\nz0V1ixoI7/MbKlaoKDoSERHJGAu5DPx8eyemn5iMihUcEN73V1SzrC46EhERyRwLWc0OPvwdXxwZ\nA0tjK/zU5xe42NQVHYmIiDQAC1mNTiecxMiDw2BsYIztH4SjSUVX0ZGIiEhD8FrWanL52UUMOfAx\nVJIKW3ruQJsqbUVHIiIiDcJCVoNbKbHw2vchcgtzsK7bJnRxek90JCIi0jAs5FL6K+MhPPf2Q0pe\nCpZ1Wom+dQaIjkRERBqI+5BLITH7KTz39MPT7Cf42j0IgxsOEx2JiIg0FAu5hFLzUjBo7wA8zHiA\niS2mYFxTP9GRiIhIg7GQSyCrIAuf7vfEzZTr8Gk8CtNbfyU6EhERaTgW8lvKV+Zj+O+DcSHxHD6q\n9zHmeSzibRSJiKjUWMhvoVBViLGHRiAy/hh61OqJ4M4h0NfjCImIqPTYJm9IJakw6bgf9t/fg3ZV\nPRDafQuMDIxExyIiIi3BQn4DkiRh9ukAhMVuR7NKzbG1VxhMDU1FxyIiIi3CQn4DS84vxNqYENS3\nbYAdvX+GhbGl6EhERKRlWMivERqzGt+dmwcny5rY2edX2Jnai45ERERaiIX8CmGx2zHzlD8qmTki\nvO9vqGJRVXQkIiLSUizkYhy4vw8Tj30BGxMb7OzzK2pbO4uOREREWqzEhbxhwwb069cPAwcORExM\nDAAgNjYWXl5e8PLywuzZs9UWsrydiD+O0RHeMDEwxY7eP6OhfSPRkYiISMuVqJDv3LmD/fv34+ef\nf8bcuXNx/PhxAEBQUBACAgIQFhaGrKwsREZGqjNrubiQeA7DDnwCAPih1w60cGwlOBEREemCEt3t\n6dixY+jZsycMDQ3RqFEjNGrUCAqFAgkJCXB1dQUAdO7cGVFRUejYsaNaA5elG8+v45N9A5GnzMWG\nHlvRoXon0ZGIiEhHlKiQExISYGBggBEjRqCwsBAzZsyAra0trKysih5jb2+PpKSkVz6Pra0ZDA0N\nShLhlRwc3v60pHsp9+C1fwDS8tOwud9mfNb0U7Xn0iQlmSH9F+eoHpxj6XGG6lGWc3xtIYeHhyM8\nPPyFZcnJyfDw8MD69etx4cIFzJw5EyEhIS88RpKk1754amrOW8Z9PQcHSyQlZb7VzzzNfoLev/TA\n06ynCGq/EL2qffjWz6FNSjJD+i/OUT04x9LjDNVDXXMsrtRfW8ienp7w9PR8YdmKFSvg7OwMPT09\ntGzZEgkJCbCzs0NaWlrRYxITE1GpUqVSxi57KXnP4bmnH+IyHmJqqxkY5eorOhIREemgEh3U1aFD\nB5w6dQoAcO/ePVSpUgVGRkZwdnbG+fPnAQARERHw8PBQX9IykKXIxCf7BuJWaixGu/piSsvpoiMR\nEZGOKtE+5KZNm+LEiRP4+OOPAQCBgYEAgICAAAQGBkKlUsHNzQ3u7u7qS6pmeYV5GPb7J7j07CK8\nGgzG3HbzeRtFIiISRk96k529ZaQs9mm8yTb+AmUBRhwcij8eHsAHzn0R2n0zDPVL9LeJVuL+JvXg\nHNWDcyw9zlA9ynofss5dqUslqTD+2Dj88fAAOlTvjDXdNrCMiYhIOJ0qZEmSMPPUNOy6/RNaOLbC\n5p7bYWJgIjoWERGRbhXywrPfYsPVdXjHrhF+/CAcFkYWoiMREREB0KFCXn15JZZeWIRaVrWxs++v\nsDW1Ex2JiIioiE4U8o83t2L2nwGobF4Fu/rugaOZo+hIREREL9D6Qt5771dMOu4HO1M7hPf5DU5W\nNUVHIiIi+g+tLuSjcYcx9tAImBmaI6z3btS3ayA6EhER0UtpbSGffRINnz+GQF9PH1t7haFppeai\nIxERERVLK0/AvZZ8FZ/u/wj5ynxs7vkj2lWT9yU8iYiItK6Q7zy/g0F7+yNTkYGQ90LRo1ZP0ZGI\niIheS6sKOSEzHv32vI/k3CQs7LAUA+sNEh2JiIjojWjNPuScghwM2tsfcelxCGgTiOGNR4qORERE\n9Ma0Zg05OTcJ8VmPML3ddIx3nSw6DhER0VvRmkJ2sqqJuyPiUbWyHe9qQkREGkdrNlkDgJGBkegI\nREREJaJVhUxERKSpWMhEREQywEImIiKSARYyERGRDLCQiYiIZICFTEREJAMsZCIiIhlgIRMREckA\nC5mIiEgGWMhEREQywEImIiKSAT1JkiTRIYiIiHQd15CJiIhkgIVMREQkAyxkIiIiGWAhExERyQAL\nmYiISAZYyERERDJgKDqAOjx//hz+/v7Iz89HQUEBZsyYATc3N8TGxuLrr78GANSvXx9z5swRG1TG\nCgsLMXPmTMTFxUGpVGLatGlo2bIlDh48iI0bN8LIyAiOjo6YP38+jI2NRceVreLmmJmZiYkTJyI9\nPR2Ojo5YunQp5/gKxc3xH2FhYVi3bh2OHj0qMKW8FTfD2NhYzJ07F/r6+rCyssKSJUtQoUIF0XFl\n61VzVHu/SFpg48aN0p49eyRJkqTo6Ghp+PDhkiRJ0pAhQ6QrV65IkiRJkyZNko4fPy4so9zt2rVL\nmj17tiRJknT79m1p4MCBkiRJUvv27aWMjAxJkiRp1qxZ0r59+0RF1AjFzXHhwoXSpk2bJEmSpO+/\n/77ofUkvV9wcJUmSkpOTJR8fH6lz586C0mmG4mY4ePDgovffggULpG3btomKqBGKm2NZ9ItWrCEP\nHz686OsnT57A0dERCoUCCQkJcHV1BQB07twZUVFR6Nixo6iYsta3b1/07t0bAGBnZ4e0tDQAgI2N\nDTIyMmBpaYmMjAzY2tqKjCl7xc3x2LFj2LZtGwDgiy++EJZPUxQ3RwBYtGgRvvzyS0ycOFFUPI1Q\n3AzXrFkDCwuL/yynl3vZHMuqX7SikAEgKSkJY8eORXZ2NrZs2YLU1FRYWVkVfd/e3h5JSUkCE8qb\nkZFR0ddbtmwpegPOmjULAwYMgKWlJRo2bAh3d3dRETVCcXNMTk7Gjh078Oeff6JOnTqYNWsWN1m/\nQnFzjI6OhomJCdzc3ERF0xjFzfCfMs7JycFvv/2G4OBgIfk0xcvmWFb9onGFHB4ejvDw8BeW+fn5\nwcPDAz///DMiIyMxY8YMzJ8//4XHSLxCaJFXzXD79u24fv061qxZA5VKhW+//Ra7du1CjRo1MGHC\nBBw5cgRdu3YVlFxe3nSOAJCfn4927drhiy++wKxZsxAeHo7BgweLiC07bzpHhUKBFStWICQkRFBS\n+Xqb9yLwdxn7+vrCx8cHLi4u5R1Xtt50jikpKS88Rm39UuqN3jIQHR0tpaWlFf27devWkkKhkDp2\n7Fi0bPfu3dKCBQsEpNMcO3fulHx8fKS8vDxJkiQpKSlJ6t27d9H3d+zYIS1fvlxUPI3x/+coSZLU\nvXv3oq8PHDhQtE+Kivf/53j58mWpe/fukqenp+Tp6Sk1atRImjBhguCU8vay92JBQYH02WefSTt3\n7hSYTLP8/zmWVb9oxWlPERER+OWXXwAAt27dQpUqVWBkZARnZ2ecP3++6DEeHh4iY8rao0ePEBYW\nhpUrV8LExAQAYGtri/T09KK/Bq9evYqaNWuKjCl7L5sjALRp0wZnzpwBAFy/fh21a9cWFVEjvGyO\nbm5uOHjwIHbu3ImdO3eiUqVKWLZsmeCk8lXcezE0NBStW7eGp6enwHSa42VzLKt+0Yq7PaWkpGD6\n9OnIzs6GQqHAzJkz0bRpU9y9exeBgYFQqVRwc3PDjBkzREeVraVLl2L//v2oWrVq0bINGzbgxIkT\nWLduHYyNjVG9enV88803L+xToRcVN8esrCxMmTIFeXl5qFixIhYsWAAzMzOBSeWtuDn+e797ly5d\neNrTKxQ3wy5duqB69epFv8dt2rThgYavUNwc4+Li1N4vWlHIREREmk4rNlkTERFpOhYyERGRDLCQ\niYiIZICFTEREJAMsZCIiIhlgIRMREckAC5mIiEgGWMhEREQy8H9xwwgy7CuqIgAAAABJRU5ErkJg\ngg==\n", - "text/plain": [ - "
\n", - "Why did I created a session to plot the graph?
\n", - "[Ans]" - ] - }, - { - "metadata": { - "id": "P3-iuxE4sjAf", - "colab_type": "code", - "colab": {} - }, - "cell_type": "code", - "source": [ - "# Let's define the placeholders\n", - "\n", - "# Placeholders?\n", - "# The input to the model changes on iteration\n", - "# So we cannot have a constant in the input as we did before\n", - "# And thus we need placeholders which we can change on each \n", - "# iteration of the training\n", - "\n", - "x = tf.placeholder(tf.float32, name='x')\n", - "y = tf.placeholder(tf.float32, name='y')" - ], - "execution_count": 0, - "outputs": [] - }, - { - "metadata": { - "id": "8hPRkaoxvRyV", - "colab_type": "code", - "colab": {} - }, - "cell_type": "code", - "source": [ - "# Let's define the linear regression model\n", - "\n", - "# tf.Variable?\n", - "# We define the model parameters as tf.Variables\n", - "# as they get updated throghout the training.\n", - "# And variables denotes something which changes overtime.\n", - "\n", - "W = tf.Variable(0.0, name='weight_1')\n", - "b = tf.Variable(0.0, name='bias_1')\n", - "\n", - "pred_y = (W*x) + b" - ], - "execution_count": 0, - "outputs": [] - }, - { - "metadata": { - "id": "cSw1P8bkv96r", - "colab_type": "code", - "colab": {} - }, - "cell_type": "code", - "source": [ - "# Let's define the loss function\n", - "# We are going to use the mean squared loss\n", - "loss = tf.reduce_mean(tf.square(y - pred_y))" - ], - "execution_count": 0, - "outputs": [] - }, - { - "metadata": { - "id": "5G4uQqjsygNj", - "colab_type": "code", - "colab": {} - }, - "cell_type": "code", - "source": [ - "# Let's define the optimizer\n", - "# And specify the which value (i.e. loss) it has to minimize\n", - "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)" - ], - "execution_count": 0, - "outputs": [] - }, - { - "metadata": { - "id": "ttI7ZT-ozAm1", - "colab_type": "code", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 721 - }, - "outputId": "d0ff4839-1198-44d8-bd4d-79d92dc1a528" - }, - "cell_type": "code", - "source": [ - "# So the graph is now built\n", - "# Now let's execute the graph using session\n", - "# i.e. lets train the model\n", - "\n", - "# What it is to train a model?\n", - "# To update the paramters in the graph (i.e. tf.Variables)\n", - "# So that the loss is minimized\n", - "\n", - "# Okay let's start!\n", - "with tf.Session() as sess:\n", - " # We need to initialize the variables in our graph\n", - " sess.run(tf.global_variables_initializer())\n", - " \n", - " for epoch in range(n_epochs):\n", - " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n", - " \n", - " if epoch % interval == 0:\n", - " print ('Loss after epoch', epoch, ' is ', curr_loss)\n", - " \n", - " print ('Now testing the model in the test set')\n", - " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n", - " \n", - " print ('The final loss is: ', final_loss)\n", - " \n", - "# Plotting the final predictions against the true predictions\n", - "plt.plot(test_X[:10], test_Y[:10], 'g', label='True Function')\n", - "plt.plot(test_X[:10], final_preds[:10], 'r', label='Predicted Function')\n", - "plt.legend()\n", - "plt.show()" - ], - "execution_count": 20, - "outputs": [ - { - "output_type": "stream", - "text": [ - "Loss after epoch 0 is 48290.105\n", - "Loss after epoch 50 is 29.782778\n", - "Loss after epoch 100 is 29.7724\n", - "Loss after epoch 150 is 29.762121\n", - "Loss after epoch 200 is 29.751879\n", - "Loss after epoch 250 is 29.741611\n", - "Loss after epoch 300 is 29.731339\n", - "Loss after epoch 350 is 29.721113\n", - "Loss after epoch 400 is 29.710855\n", - "Loss after epoch 450 is 29.700636\n", - "Loss after epoch 500 is 29.690397\n", - "Loss after epoch 550 is 29.680191\n", - "Loss after epoch 600 is 29.66994\n", - "Loss after epoch 650 is 29.65969\n", - "Loss after epoch 700 is 29.6495\n", - "Loss after epoch 750 is 29.639277\n", - "Loss after epoch 800 is 29.629047\n", - "Loss after epoch 850 is 29.618847\n", - "Loss after epoch 900 is 29.608654\n", - "Loss after epoch 950 is 29.598469\n", - "Now testing the model in the test set\n", - "The final loss is: 33.011585\n" - ], - "name": "stdout" - }, - { - "output_type": "display_data", - "data": { - "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAFKCAYAAADMuCxnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XdYU3cfBfCThBlAluBA1FYtbhHt\n6+pQHNU6ahUVZ7WOundx7713cW9xW6rWWluVqrVaFbWOCooDHChTICGEJPf9I4pVERACNyHn8zx9\nCubm5ptfKcfc5J4rEQRBABEREYlKKvYARERExEAmIiIyCgxkIiIiI8BAJiIiMgIMZCIiIiPAQCYi\nIjICFmI+eExMcr7u39lZjoQEZb4+RmHHNTQMrqNhcB3zjmtoGLldRzc3h3feVqhfIVtYyMQeweRx\nDQ2D62gYXMe84xoaRn6sY6EOZCIiIlPBQCYiIjICDGQiIiIjwEAmIiIyAgxkIiIiI8BAJiIiMgIM\nZCIiIiOQo2IQlUqFVq1aYeDAgahXrx7GjRsHjUYDCwsLLFiwAG5ubqhSpQp8fHwy7rN582bIZKZ3\nvtuKFUsQFvYv4uPjoFKpULKkB4oUccTs2QsMsn8/v9Zwdy8GqfTV34VWrlyb5/2eOfMH6tSpj6Sk\n59iwYQ0CAibkeZ9ERFRwchTIgYGBcHR0BAAsXboUHTt2xJdffokdO3Zg06ZNCAgIgL29PbZt25av\nwxaEIUNGAACOHDmEu3cjMHjwcIM/xsKFyyGXyw26z127dsDH52O4uhZlGBMRmaBsAzkiIgJ37txB\nw4YNAQBTpkyBtbU1AMDZ2Rk3btzI1wGNRWjoRezatR1KpRKDB4/AqFGD8fPPxwEAEycGoF27jqhY\nsRJmz56G5ORkaLVaDB/+PcqXr5Cj/bds2fit/V2+fAkKRQoiIx/g0aOHGDp0FOrVa4CjR3/Gvn27\nIZFI4O/fFenp6bh58zpGjx6KsWMnYdq0idiwYRtCQy9i7dofYGFhATc3d4wbNxm///4r/vnnChIT\nExAZ+QBdunRHq1Zt823diIgoZ7IN5Hnz5mHSpEkIDg4GgIxXdlqtFkFBQRg0aBAAQK1WY9SoUXj0\n6BG++OIL9OrVK8/DTT07EYcignN9f6lUAp1OeO3PWpdri6n1Z+ZqfxERd7Bz5wFYWVllevuePTtR\np059tG7dFvfu3cWyZQuxdOkPuXqsl549e4qFC5fj3Lmz+Omn/ahRwxubN6/Hli07oVanY9asKZg7\ndzHWr1+NhQuX4/nzxIz7Llw4B0uWrEKxYsWxePE8/PbbUUgkEkRE3MHq1Rvx8GEUpkwZz0AmIsrE\n30/OI0mdiCZlviiQx8sykIODg+Ht7Q1PT8/X/lyr1SIgIAB169ZFvXr1AAABAQFo06YNJBIJunXr\nhtq1a6NatWpZPrizszzLPlC5rRWkUklOn0um3ry/3NYqy3LvlxwcbCCXv9rWyUmOypUrwcPDFQAg\nkUgybrO2toSTkxxhYTcQHx+PkyePAQDS0lLfeiyZTIpx40ZkvL/u7OyM5cuXZ7o/Oztr1KtXB25u\nDvDy+gBpaal4/vwZKlQoj1Kl3AAAGzasy9hv0aL2kMnSYWEhhaWlFhYWMlStqn+F3rDhp7hw4QIq\nV66Mjz+uheLFneDgYInUVEW265GT9aLscR0Ng+uYd1zDdxMEAccijmHW6Vk4HXkacks5UsalQCJ5\nO4sMvY5ZBnJISAiioqIQEhKC6OhoWFlZoXjx4ggODkaZMmUwePDgjG07d+6c8XXdunURHh6ebSBn\nd6WMgJqTEVBzck6eR6bc3BwyvaJUTq4ylZysglKpztg2MVEJQZBkfC8IQsbXCkVqxu1DhoxC1arV\n3/lYWq0Oc+Ysee095JiY5Ez3p1CkwdLSFjExyUhIUECt1uD5cxVUKnWm+42NTcHz5wpoNDrExSmg\n0WgztouLS4JKpUFysgpqtQ4xMclQKpXQanVZrse71pDeD9fRMLiOecc1zJxO0OHI3cNYFroIV2Mu\nAwCalG6G7z8eh9jYlLe2z+065vpqT0uXLsX+/fuxZ88edOjQAQMHDkRsbCwsLS0xdOjQjO3u3r2L\nUaNGQRAEaDQahIaGokKFnL13aqokEglUKhVUKhXCw8MAAJUrV8WpUyEAgHv37mLXru152l9mypQp\ni8jIB1AqlUhLS8Pw4QMhCAIkEim0Wm3GdkWKFIFEIkF0dDQA4MqVUFSsWCkXz5SIqPDS6DTYE7YT\nn+2qg29/7YZ/Yq6gTbmvcbzDaQS12oeaxWoV2CzvfT3koKAgpKWloXv37gCAcuXKYerUqShevDj8\n/PwglUrh6+uL6tWrZ7Mn09a2rR/69fsGZct+CC8vfdD5+XXCrFlTMXBgH+h0OgwfPjpP+8uMra0t\nevfuj+HDBwIAOnXqAolEgpo1fTBwYG9MmDA1Y9uAgImYNm0CZDIZPDxKoXHjZjh27JfcPWEiokJE\npVFhd1gQVlxeisik+5BJZOjk1QVDfUaigvNHoswkEQRByH6z/JHfh014aCbvuIaGwXU0DK5j3pn7\nGirSFdh6YxN+uLIcT5XRsJZZo0ul7hjkPQyli5TJ8X7y45D1e79CJiIiMjXP0xKx/toarPsnEPGq\neNhZ2mOQ9zD0rzEIxeyKiz0eAAYyEREVYjHKGKy5ugobr69DSnoynKydMLr2WPSt3h/ONi5ij/ca\nBjIRERU6j5IfYtWVZdh+cwtUWhXcbN0xsnYAelb5FvZWxnnaFwOZiIgKjbuJd7A8dAn2hu9Cui4d\npew9MdhnODpX7AZbC1uxx8sSA5mIiEzezbgbWHZpIX6K+BE6QYdyTuUxzGcU2lfoCEuZpdjj5QgD\nmYiITNalpxew9NJC/Hpff0pn1aLVMdxnFFp+2AYyqWldcZCB/IYnTx6jRw9/eHlVBKDv6O7a9Rt8\n/nmj997X/v27kZiYiM8+a4hTp0LQu/d3mW738tKJlpbZ/y3u7t07WLx4/luXbPz88zqoVq1Gxveu\nrq6YNm3Oe8/8pqNHj6JWrQa4fTssy+dARFRQBEHAmUensDR0EU4/DAEAfFy8DkbUGo3GpZtlWnNp\nChjImShdukxG4CUlPUevXl1Rt249WFvb5Gp/FSp4oUIFr3fe/vLSiTkJ5Hext7c3yHWV37R27Vqs\nWdMg2+dARJTfBEHAbw+OYsmlhbj09AIA4PNSjTC81mjUL/mJyQbxSwzkbBQp4ghX16KIi4vDpk3r\nYGFhiaSkREyfPhfz58/C48ePoNFo0KdPf9Sq9TEuXvwby5cvgouLK1xdi6JkSQ+Ehl7EgQN7MHPm\n/CwvnbhsWSAOHvwRv/9+FBKJFJ9+2hCdO3fDs2dPMWnSWFhaWqJ8+Zw3yDx58hgTJ47Bhg3661T3\n7t0dM2fOw8aNa1G0qBvCwv7F06fRmDx5Jry8KmLHji0ICTkOiUSK/v0H49atmwgLC8P48d/Dz69T\nxnM4fvw37N69AzKZDF5elTB8+Ghs2LAm00tFEhHllVanxaGIYCwNXYSbcdcBAM0/aInhPqPgU6y2\nyNMZjlEHst3UibA+lPvLL0Iqgcsbl19Ma90Wiqk5v/zikyePkZT0HO7uxQDoO6LHjJmAo0d/hqtr\nUYwbNxmJiYkYNqw/tmzZhTVrVmLSpBmoUOEjjB49FCVLemTsS6lUZHnpxJiYZwgJOY4fftgAABgw\noDcaNWqCAwd2o3HjZujYsTO2b9+MO3fCc78mL6jVaixevBLBwftw9OjPkMvlCAk5jjVrNuPx40fY\nvn0zxo6dhKCgrZg9ewFCQy++eA5KrF27Cps2BUEulyMgYETGbW9eKpKBTER5odaqsS98N5aHLsbd\n5xGQSqRoV6EDhvmMQiXXymKPZ3BGHchiiYx8gMGD+wEArKysMHHiNFhY6JeqcuUqAIDr1//B1auX\n8c8/VwAAaWlpSE9Px5MnT1Chgv5VrLe3D9LS0jL2e//+PZQuXRbW1jawtrbB3LmLX3vcf/+9gYcP\nozBkiP59WqVSgejox7h//x4aNWoCAKhZszbOnTv71swpKSkZMwNAuXLl4e/f7Z3PsUaNmgAAN7di\nuHnzBsLDw1C5clVIpVKUKuWJsWMnZXq/qKhIlCpVOuNqVTVr1kJ4+C0AQPXq3gAAd3d3pKS8fXUU\nIqKcSNWkIujfrVh5eRkepTyEpdQS3Sv3xKCaw/ChYzmxx8s3Rh3Iiqkz3+vV7Jvc3BwQn4uu0f++\nh/wmCwvLjH/36PEtmjZt/trtUumrC2i9WRMulcogCLp3Pq6FhSXq1WuAgIAJr/35jh1bIJFIX+wz\n8/tn9h5ydPST177XaDQZX7+8HvPLOWUyKXS67GvNJZLXn5dGkw5ra+tM90lE9D6S1UnYdH0DVl9d\nidjUGNha2KJf9QEY6D0UJe09st+Bicvy8ov0bpUrV8WZM38AABIS4rFmzSoAQNGiboiMvA9BEHD5\n8qXX7pPdpRO9vCohNPQSVCoVBEHA0qULkZamQunSZXDr1k0AyDg8nBNyuR0SEuIhCALi4mLx+PHD\nd27r5VUJ165dhUajQXx8HMaN01+p6s1g9fQsg4cPI6FUKgAAly+Hwsur8B06IqKCE6+Kw7y/Z8Fn\nW1XMPDcFado0DPcZjUvdb2DmJ/PMIowBI3+FbMx8fZsgNPQC+vf/FlqtFt9+qz9c3K/fQEycOAbF\ni5fIeN/5pewunbhixVp07NgZgwb1hVQqxWefNYS1tQ06dOiMSZPG4tSpkyhXLufXmS5SpAhq1/4f\n+vTpgfLlK2T5KekSJUriiy++xODB/SAIAr77bhAAoFKlSujbtwcGDBia8RwGDRqGUaOGQCKRonp1\nb9So4Y2LF8+/1/oREUUrniDwykpsubERSo0CrjauGF9nMr6t2hdFrB3FHq/A8fKLlCWuoWFwHQ2D\n65h3xrCGD5LuY+XlZdj57zaodWqUsCuJgd5D0K1yT9hZ2ok6W07x8otERGSywuPDsPzyYuwP3wOt\noEWZImUx1GckOnp1hrXMWuzxRMdAJiKifCEIAm7G3UBI1AmciPodZx7+AQECKrpUwjCfUfiqfDtY\nSBlDL3EliIjIYJ4pn+HUw5M4GXkcfzw8iWfKpxm31Sr2MYbUHIHmH3wJqYSfKX4TA5mIiHItTZuG\nv5+cw8mo4wiJOoHrsf9k3OZm644OH/mjoacvPvf0hbvcXcRJjR8DmYiIckwQBIQnhCHkRQCffXwG\nqZpUAIC1zBqflWqEhp6+aOjpiyquVU2+X7ogMZCJiChL8ao4nIoKQUjUCYREncBjxaOM2yq6VMLn\nnr5o5OmLuiUaQG4pF3FS08ZAJiKi16i1alx6eiHjVfCVZ5chQH+GrIuNC74u3x4NPRvjc89GZlPa\nURAYyEREZk4QBNx7HoGTUSfwR9QJnH50Cop0fR+9hdQC9Uo2QENPXzTybIxqbjX4gax8wkAmIjJD\nz9MScfrhqReHoY8jMvlBxm3lnMq/eB+4MRqU/AT2Vu8usyDDYSATEZkBjU6Dy88u4cKNP3H41hGE\nPrsI3YuL1RSxckSrD7/K+DBW6SJlRJ7WPDGQiYgKqcikBwiJOoGTUcdx+uEfSFI/BwBIJVLUKvZx\nRgDXdK/Fgg4jwP8CRESFRIo6GX8+PoOTkb8jJOoE7j6PyLittEMZtC3fHl9VbYnqDh/D0dpJxEkp\nMwxkIiITpdVpcS32Kk5GHkfIwxO4EH0eGp3+uud2lvZoXvZL/SlJpRvjgyIfQiKRGMXFJShzDGQi\nIhOSpk3Dz3cP4ui9n3HqYQjiVfEAAAkk8Hav+eLT0E1Qq9jHsJRZijwtvQ8GMhGRCYhMeoCtNzYh\n6NZWxKbGAgBK2nmgS8XuaOjpi888G8LFxlXkKSkvGMhEREZKq9PiRORv2HR9PY5H/gYBApytnTGg\nxhD4V+yKii6VWE1ZiDCQiYiMTIwyBkH/bsXWm5sQlRwJQH+lpJ5VeqNN+a9ha2Er8oSUHxjIRERG\nQBAEnI8+h83X1+FQxE9I16VDbiFH98o90bNKb1RzqyH2iJTPGMhERCJKVidhb/hubLm+Af/G3wQA\nfOTshZ5VeqOjV2cUsXYUeUIqKAxkIiIR3Ii9js03NmBf+G4o0lNgIbXAV+XaoWfV3qhf8hO+N2yG\nGMhERAUkTZuGQxHB2Hx9A/6OPgcA8LAvhSE1h6Nr5W9QTF5M5AlJTAxkIqJ89iDpPrbe2ISdt7Zl\nnLLUyLMxelXtiyZlmrG2kgAwkImI8oVWp8XxyGPYfH3Da6csDfQeih5VeuFDx3Jij0hGhoFMRGRA\n7zplqVfVPmhT7mvYWNiIPCEZKwYyEVEeCYKA80/+wuYb63nKEuUaA5mIKJfedcpSr6p90OEjf56y\nRO+FgUxE9J7edcpSr6p9UK9kA56yRLnCQCYiyoF3nbI0tOYIdKncg6csUZ4xkImIsvDylKWgf7ci\nThUHAPAt3QQ9q/ThKUtkUPxJIiJ6Q2anLLnYuGCQ9zD0qNILHzh+KPaIVAgxkImIXsjslKXaxf6H\nnlV785QlyncMZCIyay9PWdp0fR0O3z344pQlO3Sv3As9q/ZGtaLVxR6RzAQDmYjMVlLac3Q90hHn\nn/wFAPByroieVXvzlCUSBQOZiMySSqPCN790wfknf6Fx6aYY6jMSdUvU5ylLJBoGMhGZHa1Oi0HH\n++HPx6fR8sM2WN9sC2RSmdhjkZmTij0AEVFBEgQB406PxqGIYNQv+QkCm6xnGJNRYCATkVlZdHEe\nNt/YgCqu1bC1xU5+cpqMBgOZiMzGlhsbMf/CbJR2KINdrfbzg1tkVBjIRGQWDkccxJhTI1HUtij2\ntP4RxeyKiz0S0WsYyERU6P356DT6//YtbC3k2NlyPz50Ki/2SGQCZNevwfL0HwX2ePyUNREVatdj\nr6HHL50hQMCm5ttRw72m2CORkZOFh8Fu3ixYHwqGIJcj9t4ToABOh8vRK2SVSoUmTZrgwIEDePLk\nCXr27Ilu3bqhZ8+eiImJAQAcPHgQ7du3R4cOHbB37958HZqIKCfuP78H/8PtkKJOxsrGa9DQ01fs\nkciISR/ch8OQ/nD+rA6sDwUj3acWnu/cXyBhDOQwkAMDA+HoqP/ww9KlS9GxY0ds374dTZs2xaZN\nm6BUKrFq1Sps3rwZ27Ztw5YtW5CYmJivgxMRZSVGGYNOh7/GM+VTzPpkHr6u4Cf2SGSkpE+jYT9m\nJFzq14LN7iBovSri+ZadSPzlBNLrNSiwObI9ZB0REYE7d+6gYcOGAIApU6bA2toaAODs7IwbN27g\n6tWrqFatGhwcHAAAPj4+CA0Nha8v/zZKRAUvRZ2MLj/74d7zuxjuMxp9qvcXeyQyQpL4OMhXLIXt\nxrWQpKZC88GHUAaMR1rb9oCs4M9Nz/YV8rx58zB27NiM7+VyOWQyGbRaLYKCgtC6dWvExsbCxcUl\nYxsXF5eMQ9lERAUpTZuGnke74WrMZXSt1APj6kwSeyQyMpLkJMgXzIFL7eqQr1oGnbMLkhctR8KZ\nC0hr31GUMAayeYUcHBwMb29veHp6vvbnWq0WAQEBqFu3LurVq4dDhw69drsgCDl6cGdnOSws8veJ\nu7k55Ov+zQHX0DC4joaR1TrqBB267O+LUw9Poo1XG2z22wALKT+7+iaz/VlMTQVWrQLmzgXi4gA3\nN2DGdMj694eDjQ3ed1UMvY5Z/qSGhIQgKioKISEhiI6OhpWVFYoXL47g4GCUKVMGgwcPBgC4u7sj\nNjY2437Pnj2Dt7d3tg+ekKDM4/hZc3NzQExMcr4+RmHHNTQMrqNhZLWOgiBgwpkA7L6xG3VK1MOK\nz9chIS61gCc0fmb5s6hWw2bHVsiXLIAs+gl0RRyROm4SlH0HAPb2QHK6/p/3kNt1zCrEswzkpUuX\nZny9YsUKeHh4IDY2FpaWlhg6dGjGbTVq1MDEiRORlJQEmUyG0NBQjB8//r0HJSLKrWWhi7D+2hpU\ncqmMbS12wdbCVuyRSGxaLaz374Hd/DmQRd6HIJdDOWwUlAOHQHB2yf7+Bey9j+UEBQUhLS0N3bt3\nBwCUK1cOU6dOxahRo9C7d29IJBIMGjQo4wNeRET5bfvNLZh9fjpK2XtiV6sDcLJxFnskEpMgwOrn\nQ7CbNxMWYbcgWFlB2ec7KIeNhlCsmNjTvZNEyOkbvvkgvw+bmOWhGQPjGhoG19EwMlvHX+79jF5H\nu8LJ2gmHvj6GCs4fiTSdaSjUP4uCAMuTx2E3ZwYsr16GIJVC5d8VylFjoPMsbdCHKvBD1kRExuzc\n47P47lgv2MhsENRyH8PYjFmc+wt2c6bD6q8/AQCqtu2gDJgAbfkKIk+WcwxkIjJJN+NuoPsv/tAI\nGmxvsRs+xWqLPRKJwOKfK5DPmQHr478BANKaNYdizERoq1UXebL3x0AmIpMTlRwJ/8Pt8DwtET80\nWQff0k3FHokK2H/7pgFA3eBTKMZPhubjOiJPlnsMZCIyKXGpceh4qC2iFU8wvcFs+H3USeyRqABJ\nH9yH3cK5sN67CxKdDuk1faAYPwXpnzUssM7p/MJAJiKTkaJOQdef/RCReAeDaw5H/xqDxR6JCoj0\naTTki+fDZvsWSNLToalUGYqxk6Bu/qXJB/FLDGQiMglqrRrd93RF6LNL6OTVBZPqThN7JCoAb/ZN\na8t+AMWYCaL1TecnBjIRGT2doMOwEwPxa8SvaFrmCyxuuAKSQvKqiDInSU6C7ZofYBu4EtLkJGhL\nlIRyxlyoOncDLC3FHi9fMJCJyKgJgoApZydg/+09qFuqLtY12wJLWeH8hUwAUlNhu2k95MsXQRof\nD52rK1Kmz0Zqzz6AjY3Y0+UrBjIRGbWVV5ZhzdVV+MjZC4c7H4ZOYSX2SJQf1GrYBG2DfPH8jL5p\nxdiJSO03AIK9eTQ/MpCJyGjturUDM/6ajJJ2Htjd6ke4yl0RoyikLVPm6s2+aVtbKIeOhHLQUKPs\nm85PDGQiMkrH7v+CEScHw8naCbtb/wgPh1Jij0SG9GbftKWlSfRN5ycGMhEZnb+fnEffYz1hJbPC\njpZ74eVSUeyRyFBe9k3PnQHLK/q+6dQu3fOlb9rUMJCJyKiExd9CtyMdoNaqsbXFTnxc3HSbl+h1\nb/VNf9UOyoDx0FZgBznAQCYiI/Io+SE6HfoaiWmJWO4biKZlm4s9EhnAW33TTb+AYuwkk+ybzk8M\nZCIyCvGqOHQ6/DUeKx5hUr3p8K/YVeyRKI/e6puu/wkU46dA8z8e9cgMA5mIRKdIV6Drzx0RnhCG\n/jUGY7D3MLFHojyQRj7Q903v2fmqb3rcZKR/3qjQ1FzmBwYyEYkqXZuOvr9+g0tPL6B9hY6YWn8m\nW7hMlPRpNORLFsBm22Z933TFSvq+6RYtGcQ5wEAmItEIgoARIYPxe+QxNPJsjGW+P0AqkYo9Fr0n\nSXwc5CuXwXbDmld90wHjkfa1X6Hrm85PDGQiEs2Mc1OwJ2wnfNxrYUPzbbCSsYXLlEhSkmG7epVZ\n9U3nJwYyEYki8MpKrLy8FOWdKmBHy32wt7QXeyTKqZd90ysWQxoXZ1Z90/mJgUxEBW5v2C5MOTse\nxe1KYHfrH+Fq6yr2SJQT6en6vulF8/R90w5FzK5vOj8xkImoQJ2I/A3DTg6Eo7UTdrf6EZ4O5t3O\nZBJe9k0vmAPZA/Pum85PDGQiKjCXnl7At0e7w0JigW0tdqGSa2WxR6KsCAKsjhyG3dwZGX3Tqb37\nQTl8NHTFios9XaHDQCaiAnE7IRxdf+4AlVaFzc2DULdkfbFHoncRBFiGnIDdnOmv+qY7d9P3TZcu\nI/Z0hRYDmYjy3eOUR+h06GvEq+KxpOFKNP/gS7FHonewOH9O3zd99gwA9k0XJAYyEeWrRFUC/A+3\nw8OUKIyvMxldK/cQeyTKhMW1q/q+6d+PAdD3TSvHToSmWg2RJzMfDGQiyjepmlR0O9IJt+L/RZ9q\n32GYzyixR6I3yG6HQz5vFmwO/giAfdNiYiATUb7Q6DTod6wn/o4+h7bl22HmJ/NYiWlE2DdtfBjI\nRGRwgiBgdMgw/Hr/F3xWqhFWNF7DSkxjER0N+4lTYLN1E/umjQwDmYgMbs75GQi6tQ013Gpic/Pt\nsJZZiz2S2ZMkxEO+chmwfjVsU1OhLVMWijET2DdtRBjIRGRQ6/4JxNLQhfjA8UMEtdwHeys2OIlJ\nkpIM2zU/wPaHFZAmJwEeHkgeEcC+aSPEQCaiHBMEAWnaNKi1aVC9+HeaVoU0rRppGhUux4Riwpkx\ncJcXw57WwXCTu4k9svlKTYXt5g2QL1/0Wt+0/ejhUKVoxJ6OMsFAJjIBOkEHtVb9Kvy0Kn0oal6G\n4st//nu7GqoX26Vp0l58nZN9vAzcN7bXqKDWqbOd1cGqCHa1OoAyRcrm/8LQ2172TS+eD9mTx2/1\nTdvb2gIpyWJPSZlgIBMZoeux1zD4+HeITHoAtTYtR0FoCFKJFDYyG1jJrGAts4G1zBrO1i6wklnD\nxsIaVjJrWGf8Y/PqawtrWEn127Qp1w5VilYtkHnpP7RaWP+4D3bzZ0N2/56+b3rICCgHD2PftIlg\nIBMZmVMPQ9Dzl65ISU9GZdeqsLWwgfWLkNSHpXWmQWiVEZJWb23/3zDNdB8v/txCyl8JJudl3/S8\nmbC49S/7pk0Y/+8jMiL7w/dg6IkBkECCNU034usKfmKPRMZKEGD5x0l93/TlUPZNFwIMZCIjIAgC\nVl1Zjul/TUIRK0dsaRGEBh6fij0WGSmLv8/r+6b/PA2AfdOFBQOZSGRanRaT/hyL9dfWoIRdSexs\ntR+VXauIPRYZIdm1f2A3dwasf/sVAPumCxsGMpGIVBoVBv7eF4fv/oSKLpWws+V+eDiUEnssMjKy\nO7f1fdM/HQDwom963GRo6tQVeTIyJAYykUgSVPH45pcuOPfkLOqX/ARbWgTB0dpJ7LHIiEijIiFf\nOBc2u4P0fdPeNaEYP4V904UUA5lIBA+To+B/uB3CE8LwVbl2WNlkDeslKYPk6VPYLV3Avmkzw0Am\nKmDXY6+hy89+iFY8Qf8agzG1/kxeeIEAvOqbtl2/GpKXfdMB45HWrgP7ps0AA5moAP33HOPpDWaj\nf43BYo9ERkCSkgzbtYGwXbVOZRLKAAAgAElEQVQc0uQkaEuUhHL6HKi6dGfftBlhIBMVkH3huzHs\nxEBIIMHappvQtkJ7sUcisalUsN28HvJl/+mbnjYbqT17A7a2Yk9HBYyBTJTPBEHA/D/nY8zvY3iO\nMemlp8Nm53bIF8171Tc9ZgJSvxsIwZ5XxzJXDGSifPTmOca7Wh1AJdfKYo9FYnlX3/SgoRBcXMWe\njkTGQCbKJ6maVAz8vS9+vnsQVd2rYnvzvShp7yH2WCQGQYDVLz/r+6b/vcm+acoUA5koHySo4tHj\nl844/+QvNCj5KQ53P4j0ZH5K1uxk0jet8u8Kxeix7JumtzCQiQwsKjkSnQ+3R3hCGNqWb4cVjdfA\nycYJMcm8Bq05eatvus3XUI6ZwL5peicGMpEBXY+9hs6H2+OpMhoDagzBlPozeI6xmXmrb7pJMyjH\nTWLfNGWLgUxkIC/PMVakp2BGgzn4rsYgsUeiAvRW33S9BlCMn8K+acoxBjKRAbx2jnGzTfiqfDux\nR6ICkmnf9LjJSG/oy5pLei8MZKI8EAQBK68sw4y/JqOIlSO2ttiJ+h6fiD0WFQDJ06eQL1sI2y0b\n9X3TXhX1fdNftmIQU64wkIly6b/nGJe088DOVvt5jrEZkCTEQ75qub5vWqlk3zQZDAOZKBf+e45x\nJZfK2NlqP88xLuTe6psuXgLKqbP0fdNWVmKPR4UAA5noPSWo4tH9iD/+jj6HBiU/xeYWO3gd48Ls\nzb5pFxekTJ2F1F592DdNBpWj8zFUKhWaNGmCAwf0nx7cunUrqlSpAoVCkbFNlSpV0L1794x/tFpt\n/kxMJKKo5Ei0OtAMf0efw9fl22NX6wMM48IqPR02WzfBpW5N2E8eD6jToQgYj/gL/yB14BCGMRlc\njl4hBwYGwtHREQAQHByMuLg4uLu7v7aNvb09tm3bZvgJiYzEtdh/0OWwH54qozHQeygm15vOc4wL\nI51O3zc9b9arvunBw6EcPIx905Svsg3kiIgI3LlzBw0bNgQANGnSBPb29jh06FB+z0ZkNP6IOole\nR7tBkZ6CmQ3mol+NgWKPRIYmCLA6egR2c2e86pv+ti+UI75n3zQViGz/ej9v3jyMHTs243t7e/tM\nt1Or1Rg1ahT8/f2xadMmw01IJLK9YbvQ+ef2UGvTsK7ZZoZxYSMIsAw5AacWvnD8pjNkYbeg8u+K\n+L9CkTJ3EcOYCkyWr5CDg4Ph7e0NT0/PbHcUEBCANm3aQCKRoFu3bqhduzaqVauW5X2cneWwsMjf\n0wTc3Hht0bwy1zV8eR3jscfHwsnGCcGdgvF52c9zvT9zXUdDM+g6nj0LTJgAhITov/fzg2T6dNhU\nqgQbwz2K0eHPomEYeh2zDOSQkBBERUUhJCQE0dHRsLKyQvHixVG/fv23tu3cuXPG13Xr1kV4eHi2\ngZyQoMzl2Dnj5uaAmBgW+ueFua6hVqfFxD/HYMO1tShp54FdrQ+gol2lXK+Fua6joRlqHd/qm27c\nVN83Xd1bv0Eh/m/Fn0XDyO06ZhXiWQby0qVLM75esWIFPDw8Mg3ju3fvYtWqVVi4cCG0Wi1CQ0PR\nvHnz9x6UyBikalIx4Lc+OHLvECq5VMHOVvt4jnEhIbtzG/L5s2AT/KJvum59fd903XoiT0aUi/OQ\nAwMDcfbsWcTExKBv377w9vZGQEAAihcvDj8/P0ilUvj6+qJ69er5MS9RvvrvOcafeHyGzc13oIi1\no9hjUR5JoyIhXzQPNrt26Puma9SEYtwkpDdqzJpLMhoSQRAEsR48vw+b8NBM3pnTGkYlR8L/UDvc\nTgxHuwp+WOYbCGuZtUH2bU7rmJ/edx0z+qa3boJErdb3TY+ZCHXL1mYbxPxZNIwCP2RNZC6uxf6D\nzofb45nyKQZ5D8OketN4jrEJe6tvunRZKALGIa19R/ZNk9FiIJPZC4k6gW+Pduc5xoVARt/0Dysg\nTXrOvmkyKQxkMmt7wnZi+MlBkElkWP/FFrQu11bskSg3VCrYbtmg75uOjWXfNJkkBjKZJUEQsOLy\nEsw8NxWO1k7Y2mIn6pVsIPZY9L7S02Gzawfki+ZB9vgRdPYOUASMR+p3AyE4FBF7OqL3wkAms6PV\naTHhTAA2Xl8HD/tS2NlqPyq6VBJ7LHof7JumQoiBTGblzXOMd7XajxL2JcUei3JKEGD1y8+wmzsT\nFv/e0PdN9+qj75suXkLs6YjyhIFMZiNeFYfuR/xxIfo8zzE2NYIAy1MhwIJZcPz7bwhSKVSdukAx\neix0ZcqKPR2RQTCQySxEJj2A/+F2uJN42+DnGFP+srhwHnZzZsDqzCkAQFrrtlCMmQDtR14iT0Zk\nWAxkKtTUWjV2hwVh7vmZiEl9xnOMTYjs+jV93/SxowD0fdPW8+ciybOCyJMR5Q8GMhVKKo0KQbe2\nYUXoEjxKeQhrmTVmfzIffar3F3s0yoYs4jbk8zLvm3ZzcyjUF34g88ZApkJFma7E9pubsfLKMkQr\nnsDWwhbfVR+IQTWHobgdP/RjzDL6pncHQaLVsm+azA4DmQqFlPQUbLm+EauuLENsagzkFnYYXHM4\n+tcYDHe5u9jjURYkz57p+6a3bGTfNJk1BjKZtGR1EjZeW4fAqysQr4qHvaUDRtQajX7VB8HVluej\nGjNJYoK+b3pdIPumicBAJhOVqErAumurse6fQCSmJcLR2gnffzwOfav1h5ONs9jjUVZSUiBfFwjb\nVcv1fdPFirNvmggMZDIx8ao4rLm6CuuvrUWyOgkuNi4YX2cyelfrBwcrViUatcz6pqfMROq3fdk3\nTQQGMpmIGGUMAq+uwMZr66DUKFDU1g0j6s1Az6q9YW9pL/Z4lBX2TRPlCAOZjNpTRTRWXlmGrTc2\nIlWTimLy4hhXZyK6V+4FuaVc7PEoKzodrIP3Qz5vFizu3YVgYwPloGFQDhnOvmmiTDCQySg9Sn6I\nFZeXYMe/W5GmTYOHfSkMrjkcXSv1gI2FjdjjUVYEAVa//gK7OTPYN030HhjIZFQikx5gWehi7Lq1\nHem6dJQuUhbDfEaik1cXWMn4gR9jZ3kqBHazp8Ey9BL7poneEwOZjMLd5xFYdmkR9obvgkanwQeO\nH2JEre/RvkJHWMosxR6PsmFx8W993/TpPwCwb5ooNxjIJKrbCeFYcmkBDtzeC52gw0fOXhheazTa\nlm8PCyl/PI2d7MZ1fd/0r78A0PdNK8dNgqa6t8iTEZke/sYjUfwbdxNLLs3HT3d+hAABlVyqYGTt\n79Hqw68gk7IUwtjJIm5DPn82bH7cD+D1vmkiyh0GMhWoazFXsejifBy5dwgAUK1oDYysHYAWH7Tk\nFZhMgPRhlL5vetcO9k0TGRgDmQpE6NOLWHxxPo490F9Kz8e9FkbVHoMmZb6AhL/Ijd5bfdMfeUEx\ndhL7pokMiIFM+er8k3NYfHEeTkYdBwD8r3hdjKo9Bg09fRnEJiDTvunvxyLNrxP7pokMjIFMBicI\nAs4+PoPFF+fj9CP9p24/8fgMI2sHoEHJTxnEpiAlBfL1q2G7ctmrvukpM6Hq2oN900T5hIFMBiMI\nAv54eBKLL87HuSdnAQANPX0xsvYY1C3BD/uYBJUKtls3Qr50EaSxMeybJipADGTKM0EQcDzyGBZd\nnIdLTy8CAJqW+QIjawegVrGPRZ6OckSj0fdNL5z7qm/6+3FI7T+IfdNEBYSBTLkmCAKO3j+CxRfn\n42rMZQBAiw9aYWSt71HDvabI01GOvOybnj8bFncj2DdNJCIGMr03naDD4YifsPjSAtyMuw4JJGhT\n7muMqPU9qhStKvZ4lBMv+6bnzoTFzesQLCzYN00kMgYyvZe/n5zHqJAhCEu4BalEinYVOmBEre/h\n5VJR7NEohyxP/6Hvm750Ud833bGzvm+67Adij0Zk1hjIlCNanRYrLi/BvL9nQYCATl5dMLzWKJRz\nqiD2aJRDb/VNt/pK3zftxb9MERkDBjJlK1rxBIN+74fTj/5ACbuSCGyyHvU9PhF7LMqhN/um1b5N\noBg3CZoafJ+fyJgwkClLR24fQY8DPRCnisMXZVtgaaMf4GrLD/uYgpd909bBByARBKTXqQfFhClI\nr1tf7NGIKBMMZMqUWqvGzHNTsfrqSlhJrTDrk3noU60/Sz1MgPTRQ33f9M7t+r7p6t5QjJ+E9EZN\nWHNJZMQYyPSWu88j0P/Yt7gScxkVXCpgdeONqOZWQ+yxKBuSZ88gX74Itps3vOqbHjMR6lZtGMRE\nJoCBTK/ZF74b3/8xAor0FHTy6oL17dYg9bkg9liUBUliAmx/WAH52h9e9E2XgeL7ceybJjIxDGQC\nAKSkp2DcqdHYHRYEO0t7rGq8Fh28/GFvZY9UJIs9HmXmZd/0quWQPk9k3zSRiWMgE67F/oN+x3oi\nIvEOarjVxJqmG/ChU3mxx6J3ebNv2tkZKZNn6Pum5XKxpyOiXGIgmzFBELDh2hpMPTsRap0a/WsM\nxsS6U2El46sro6TRwGZ3kL5v+tFDfd/06LFIHTCYfdNEhQAD2UzFq+Iw/MQgHL1/BK42rljReDWa\nlPlC7LEoMzodrH86APm8Wa/6pgcOhXLICAiuPAWNqLBgIJuhs4/OYMDvffBE8RifeHyGH5qsQ3E7\n9hcbHUGA1bGjsJsz41XfdM/eUI4MYN80USHEQDYjWp0Wiy7Ow+JL8yGBBOP+NwlDfUZCJuUncY2N\nvm96OiwvXYAgkbBvmsgMMJDNxOOURxjwex/89fhPlLL3xOqmG/G/EnXEHoveYHHpAuxmz4DV6RAA\nQFrLNvq+6YqVxB2MiPIdA9kMHL13BMNODEBCWgJaffgVFjdcDicbZ7HHov+Q3bgOu3kzYX30CABA\n3aixvm/a20fkyYiooDCQCzGVRoXpf03C+mtrYCOzwfzPluCbKt+y/tKIyO7e0fdN/7j/Vd/0+MlI\nr9dA7NGIqIAxkAupOwm30fdYT9yIu4aPnL2wttlmVHatIvZY9MJbfdPVakAxYTL7ponMGAO5kBEE\nAbvDgjD21CgoNUp0r9wTMxrMhdyShRHGQBITA/myha/6pit8BMXYiVC3bANIpWKPR0QiYiAXIsnq\nJHz/xwgcuL0XDlZFsK7ZZnxVvp3YYxEAJCRAPns25GsDIVEq9H3To8cirYM/+6aJCAADudC48iwU\n/Y71wv2ke6hVrDZWN92IMkXKij0WKRSwXb8aWLUMdomJ0LoXg3LydKi6fcO+aSJ6DQPZxOkEHVZf\nXYVZ56ZCo9NgaM2RGPO/CbCUWYo9mnlLS9P3TS9ZCGlsDODiwr5pIsoSA9mExShjMPREfxyP/A1u\ntu5Y1WQtGnr6ij2WeXuzb9rOHopRY2A3aRxS1XyPmIjejYFsok49DMHA3/vimfIpGnk2xorGa+Au\ndxd7LPP1sm96/mxYRNx5q2/aztEBiOFlLIno3RjIJiZdm44FF+ZgWegiyKQyTK43AwO9h0Aq4asv\nUWTWN/1NbyhHfg9diZJiT0dEJoSBbEIikx6g/2+9cfHp3yhTpCzWNN0In2K1xR7LbFmeOQW7WdNe\n9U138Ifi+3HsmyaiXGEgm4hDEcEYcXIIktTP8XX59ljw+VIUsXYUeyyzxL5pIsoPOTrOqVKp0KRJ\nExw4cAAAsHXrVlSpUgUKhSJjm4MHD6J9+/bo0KED9u7dmz/TmqFUTSpGhwxH7197QKNLx9JGq7C6\n6UaGsQhkN66jSA9/OLdoDKvTIVA3aoyEYyFI2rSdYUxEeZajV8iBgYFwdNQHQHBwMOLi4uDu/uoD\nREqlEqtWrcK+fftgaWkJPz8/NG3aFE5OTvkztZm4Ff8vvjvWC//G30Rl16pY23QTPnLxEnsss/NW\n3/T/6ur7put/IvZoRFSIZBvIERERuHPnDho2bAgAaNKkCezt7XHo0KGMba5evYpq1arBwcEBAODj\n44PQ0FD4+vIUnNwQBAHbbm7GpD/HIlWTim+r9sXU+rNgY2Ej9mhmJbO+aeX4SVD7NmXfNBEZXLaB\nPG/ePEyaNAnBwcEAAHt7+7e2iY2NhYuLS8b3Li4uiImJMeCY5uN5WiJGhQzDwYgf4WTthB+arEfL\nD1uLPZZZkcTEQL58EWw3rWffNBEVmCwDOTg4GN7e3vD09HyvnQqCkKPtnJ3lsLDI3x5fNzeHfN2/\nIZ17eA7++/zx4PkDfFL6E+xotwOlHUuLPZZJrWGeJCYCCxcCS5cCCgVQpgwwdSosunWDo0XeP/9o\nNuuYz7iOecc1NAxDr2OWv2VCQkIQFRWFkJAQREdHw8rKCsWLF0f9+vVf287d3R2xsbEZ3z979gze\n3t7ZPnhCgjKXY+eMm5sDYkygjEEn6LDy8lLMOT8DOkGHUbXHYFTtMbBQW4g+v6msYZ686JuWr1wG\n6fMXfdMTp+n7pq2tgYTUPD+EWaxjAeA65h3X0DByu45ZhXiWgbx06dKMr1esWAEPD4+3whgAatSo\ngYkTJyIpKQkymQyhoaEYP378ew9qjp4qn2LQ7/1w6uFJFLcrgcAm69HA41OxxzIPb/RN65yckDJp\nOlJ792PfNBEVuPc+DhcYGIizZ88iJiYGffv2hbe3NwICAjBq1Cj07t0bEokEgwYNyviAF2XuScpj\n7A3fhdVXVyE2NQbNyjTHMt9AuNq6ij1a4feyb3rRPMgeRmX0TacOGAyhCE8nIyJxSIScvuGbD/L7\nsImxHZpRpivxy73D2HVrB049DIEAATYyG0yqNw19qvWHxAg/uWtsa5gnb/ZNW1sjtVdfKIeOhFC0\naL4+dKFaRxFxHfOOa2gYBX7ImvJOEAScf/IXdocF4ac7PyIlXf8fsHax/6FTxS74qtzXcLJxFnnK\nQk4QYPXbUdjNZt80ERkvBnI+eZB0H3vCdmJP2E48SLoPAPCwL4W+1b9DR6/OKOdUQdwBzcRbfdN+\nnfR90x98KPZoRESvYSAbUIo6GYcifsLusCCcfXwGACC3kKPDR/7wr9gVDTw+5VWZCshbfdNfttb3\nTVeqLO5gRETvwEDOI52gw5lHp7Dr1g4cuXsISo3+VK4GJT9Fp4pd0OrDNrC34gfcCors5g3YzZ0J\n66M/AwDUDX2hGDcJmpq1RJ6MiChrDORciki8jd23dmJv+C48SnkIAChTpCw6eXVBR6/OKF2kjMgT\nmhfp3QjYzZ8N6x/3sW+aiEwSA/k9JKoSEHznAHaHBeHS0wsAAAerIuhW6Rt0rNgFdYrXNcpPShdm\n0kcPIV88HzZB2/R901Wr6/umGzdj3zQRmRQGcjY0Og1Coo5j962dOHr/Z6Rp0yCVSNHQ0xf+Fbui\nedmWkFuyRKKgZfRNb94ASVoaNOUr6PumW33FvmkiMkkM5He4GXcDu28FYf/tPXimfAoA+MjZCx29\nuqDDR51Qwp6ny4hB8jwRtj8sh3xNICRKBbSepaH4fhzS/DoBBuibJiISC3+D/UdsaiwOhO/B7rCd\nuBZ7FQDgZO2EXlX7wN+rK7zdfXhIWixv9E3r3NyRMmkqVN166vumiYhMnNkHslqrxm8PfsXusCD8\n/uBXaHQayCQyfFG2BTp6dUGzss1hLeMvfNGkpcFm2ybYLVkIacwzfd/0xGn6vmk7O7GnIyIyGLMM\nZEEQ8E/MFewK24Efb+9DvCoeAFDFtRr8K3ZBuwod4SZ3E3lKM6fRwGbPTsgXzn3VNz0yAKkDh7Bv\nmogKJbMK5KeKaOwN3409YUG4Ff8vAKCorRu+qzEInby6oGrRaiJPSNDpYH3wR8jnzcrom1b2H1wg\nfdNERGIq9IGcqknF0Xs/Y3dYEEKiTkAn6GAltULrcm3RyaszGnk2gaXMUuwx6WXf9JyZsLhxTd83\n3eNbfd90SQ+xpyMiyneFMpAFQcCF6L9x8Nxe7Lq+G0nq5wAAH/da6FixC74u3x7ONi4iT0kvWZ45\nBbvZ02F58W/2TROR2SpUgRyVHIm9YbuwJ2wn7j6PAACUsCuJnlV6o6NXZ3zk4iXyhPRfFqEX9X3T\np04CYN80EZm3QhPIR+8dwTe/dIYAAbYWtmhXoQP61+mLavYfQyaViT0e/cdbfdOfN4Ji/GT2TROR\nWSs0gVzSviRalfsKvp5N0KZ8WzhYFeGFuI3MW33TH9fR9003+FTs0YiIRFdoArm6mzc2fLFV7DEo\nE+ybJiLKXqEJZDI+mfVNK8dMQFrrtuybJiJ6AwOZDE7yPBG2gSsgX/2Dvm+6lKe+b7qDP/umiYje\ngb8dyXAUCthuWAP5yqWQJrJvmojofTCQKe/YN01ElGcMZMq9N/qmBbmdvm96wGAIjk5iT0dEZFIY\nyPT+dDpYHwqGfO7MV33T3w3S90278aIcRES5wUCmnBMEWP3+K+xmz9D3TctkSO3eC8pRAeybJiLK\nIwYy5Yjln6dhN2vaq77pdh2gCBgP3YflxB6NiKhQYCBT1v7+G47fj33VN92iFRRjJ7JvmojIwBjI\nlCnZvzdhN3cm8MthWOFF3/S4SdD41BZ7NCKiQomBTK+R3o2A3YI5sD6wFxJBAOrXR+L3E9g3TUSU\nzxjIBACQPn4E+aL5sNm5DRKNBpoq1aAYPwmOnf2QHpsi9nhERIUeA9nMSWJjIV+2CLab1+v7psuV\nh3LsxFd907z4AxFRgWAgm6mXfdO2awIhVaSwb5qISGT8zWtuFArYblgL+colGX3TyRMmQ9W9F/um\niYhExEA2F2lpsNm+GXaLF/ynb3oqUnt/x75pIiIjwEAu7DQaWO/dBbsFc/7TN/09UgcMYd80EZER\nYSAXVi/7pufNgsWd2+ybJiIycgzkwuZF37R8zkxYXv+HfdNERCaCgVyIWJ49o++bvnCefdNERCaG\ngVwIWFy+BLvZ02H1x4u+6eYt9X3TlauIPBkREeUUA9mEveybtv7lMABA/VkjKMZNhKbWxyJPRkRE\n74uBbIKk9+7q+6b374FEEJBe+39QjJ+M9E8+E3s0IiLKJQayCZE+eazvmw7a+lrftLrJF6y4JCIy\ncQxkEyCJjYV8+WLYblr3qm96zASktfla3zdNREQmj4FsxCRJz2H7wwrYrvlB3zftUQrK78dB1bEz\n+6aJiAoZ/lY3RkolbNevedU3XdSNfdNERIUcA9mYqNWw2bYZ8iULIHv2FDpH9k0TEZkLBrIx0Ghg\nvW+3vm86KpJ900REZoiBLCadDlaHf4LdvFmwuB3+om96IJRDR7FvmojIzDCQxSAIsDp+TN83fe3q\ni77pnlCODIDOo5TY0xERkQgYyAXM8uwZ2M2eDsu/z73om/aDMmA8tB+WF3s0IiISEQO5gFhcCdX3\nTYecAMC+aSIieh0DOZ/Jbv2r75s+cggA+6aJiChzDOR8wr5pIiJ6HwxkA8u0b3rcRKibNmffNBER\nvRMD2UAkcXGv+qZVKmg+LAfl2InsmyYiohxhIOeRJOk5bANXwnb1KvZNExFRruUoMVQqFVq1aoWB\nAweiXr16CAgIgFarhZubGxYsWAArKytUqVIFPj4+GffZvHkzZDJZvg0uOqUSthvW6vumExLYN01E\nRHmSo0AODAyEo6MjAGD58uXo0qULWrRogcWLF2Pfvn3o0qUL7O3tsW3btnwd1iiwb5qIiPJBtm9u\nRkRE4M6dO2jYsCEA4Pz582jcuDEAoFGjRvjrr7/ydUCjodHAetcOuNSvBYdxoyFNSYFixGjEX/wH\nqUNHMoyJiChPsg3kefPmYezYsRnfp6amwsrKCgDg6uqKmJgYAIBarcaoUaPg7++PTZs25dO4ItDp\nYHXwRzh/XhdFhg6A9Gk0lN8NRNyFf6AcN5kXfyAiIoPI8pB1cHAwvL294enpmentgiBkfB0QEIA2\nbdpAIpGgW7duqF27NqpVq5blgzs7y2Fhkb/vM7u5OeTujoIA/PILMHEicPkyIJMBfftCMmkS5J6e\nkBt2TKOW6zWk13AdDYPrmHdcQ8Mw9DpmGcghISGIiopCSEgIoqOjYWVlBblcDpVKBRsbGzx9+hTu\n7u4AgM6dO2fcr27duggPD882kBMSlAZ4Cu/m5uaAmJjk976f5V9/wm7WtIy+6bR2HaAMGPeqbzoX\n+zRVuV1Deh3X0TC4jnnHNTSM3K5jViGeZSAvXbo04+sVK1bAw8MDly9fxq+//oqvvvoKx44dw6ef\nfoq7d+9i1apVWLhwIbRaLUJDQ9G8efP3HlRs7JsmIiKxvPeJskOGDMGYMWOwe/dulCxZEm3btoWl\npSWKFy8OPz8/SKVS+Pr6onr16vkxb75g3zQREYlNIvz3jeAClt+HTbI7pCC9f0/fN71vN/um34GH\ntwyD62gYXMe84xoaRoEfsi6spE8eQ754AWx2bGHfNBERGQWzCmT2TRMRkbEyi0Bm3zQRERm7wp1G\nSiVsVyxl3zQRERm9whnIL/qmsWwh7KOj2TdNRERGr3AFskYD6327YbdwLmSRDwA7OyhGjEbqwKGs\nuCQiIqNWaAJZdjscRXp2gcXtcAjW1lB+NxDy6VOglNiKPRoREVG2Ck0gW9y4Btm9u0jt3hPKkQHQ\neZSC3M3BrGouiYjIdBWaQE5r2x5prdvqLwJBRERkYgrXybcMYyIiMlGFK5CJiIhMFAOZiIjICDCQ\niYiIjAADmYiIyAgwkImIiIwAA5mIiMgIMJCJiIiMAAOZiIjICDCQiYiIjAADmYiIyAgwkImIiIyA\nRBAEQewhiIiIzB1fIRMRERkBBjIREZERYCATEREZAQYyERGREWAgExERGQEGMhERkRGwEHuAvJo/\nfz4uXboEjUaD7777Ds2aNQMAnD59Gn369EFYWBgA4NatWxg/fjwAoHHjxhg0aJBoMxujnK7jkiVL\ncP78eQiCgCZNmqBv375ijm1U3lzDEydO4MaNG3BycgIA9O7dGw0bNsTBgwexZcsWSKVSdOzYER06\ndBB5cuOS03U8cuQINm7cCKlUinr16mHEiBEiT25ccrqOL40cORJWVlaYO3euSBMbn5yuocHyRTBh\nf/31l9CnTx9BEAQhPpxGHhcAAATPSURBVD5e+PzzzwVBEASVSiV069ZNaNCgQca2fn5+wvXr1wWt\nViuMGDFCUCqVYoxslHK6jmFhYUKnTp0EQRAErVYrNG/eXHj27JkoMxubzNZwzJgxwokTJ17bTqFQ\nCM2aNROSkpKE1NRUoWXLlkJCQoIYIxulnK6jUqkUGjVqJCQnJws6nU7w8/MTbt++LcbIRimn6/jS\nmTNnhPbt2wtjxowpyDGN2vusoaHyxaRfIX/88ceoXr06AKBIkSJITU2FVqvF6tWr0aVLFyxYsAAA\nEBsbC6VSiSpVqgAAFi9eLNrMxiin6+jg4IC0tDSo1WpotVpIpVLY2tqKObrReNcavunq1auoVq0a\nHBwcAAA+Pj4IDQ2Fr69vgc5rrHK6jra2tjh48CDs7e0BAE5OTkhMTCzQWY1ZTtcRANRqNQIDAzFg\nwAD89ttvBTmmUcvpGhoyX0z6PWSZTAa5XA4A2LdvHz777DNERkbi1q1baNGiRcZ2jx49gqOjI8aO\nHQt/f39s3rxZpImNU07XsUSJEmjevDkaNWqERo0awd/fP+MXornLbA1lMhm2b9+OHj16YMSIEYiP\nj0dsbCxcXFwy7ufi4oKYmBixxjY6OV1HABk/e2FhYXj06BFq1Kgh2tzG5n3Wcc2aNejcuTP/X35D\nTtfQoPmSp9f0RuK3334T/Pz8hKSkJKFv377CgwcPBEEQhEaNGgmCIAiXL18WPv30UyE+Pl5QKpVC\n69athfDwcDFHNkrZrWNkZKTQvn17QalUCklJScKXX34pxMbGijmy0fnvGp49e1a4efOmIAiCsGbN\nGmHatGnCwYMHhVmzZmVsv3jxYmHXrl1ijWu0slvHl+7duye0atUq43Z6XXbreO/ePaFfv36CIAjC\nuXPneMg6E9mtoSHzxaRfIQP6Dx2tXr0a69atg1KpxN27dzF69Gh07NgRz549Q7du3eDq6ooKFSrA\n2dkZtra2qFWrFm7fvi326EYlJ+t47do11KhRA7a2tnBwcICXlxfCw8PFHt1o/HcNHRwcUK9ePVSq\nVAkA4Ovri/DwcLi7uyM2NjbjPs+ePYO7u7tYIxulnKwjAERHR2PQoEGYO3duxu30Sk7WMSQkBI8f\nP0bHjh0xbdr/27tDVYXhKI7jZ019BPEBDL6BmLRpEnFgEsWkYWCyeZNYrVafwWwWm8Eo6AMMRRCE\ncW64OLhchQljHi/fTxz/cPiV3w77w75ktVrJfD5/8+R2RMkw1n6J800iaefzWWu12tMt7b7Zqaq6\nrqu+72sQBOq6ru52u6TGNC9qjtvtVpvNpgZBoLfbTavVqh6PxyRHNetRhoPBQA+Hg6qqLhYLHY/H\ner1etVKp6Ol00svlEl7wwo+oOaqqdjodXa/Xb5nTuldyvGND/u2VDOPql4++1LVcLsX3ffE8L3w2\nnU4lm83+OTsajaTX64njOFIqlSSfzyc5qmlRcywUClIsFqXVaomISKPRkFwul+isVj3KsF6vi+d5\nkk6nJZPJyGQykVQqJcPhULrdrjiOI/1+P7zgheg57vd72Ww2MpvNwnPtdlvK5fI7xjYnao547pUM\n4+oXfr8IAIABH/8NGQCA/4BCBgDAAAoZAAADKGQAAAygkAEAMIBCBgDAAAoZAAADKGQAAAz4Bk8v\ndOjNfm9CAAAAAElFTkSuQmCC\n", - "text/plain": [ - "
\n", - "\n", - "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n", - "\n", - "Or better, do it yourself!" - ] - }, - { - "metadata": { - "id": "OZ5TY7B_4E_v", - "colab_type": "code", - "outputId": "5f7cfdb6-e69e-40ea-a4e1-4e0eca574301", - "colab": { - "base_uri": "https://localhost:8080/", - "height": 415 - } - }, - "cell_type": "code", - "source": [ - "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n", - " # YOUR CODE HERE\n", - "\n", - " x = tf.placeholder(tf.float32 , name = 'x')\n", - " y = tf.placeholder(tf.float32 , name = 'y')\n", - " W = tf.Variable(0.0 , name = 'Weight_1')\n", - " b = tf.Variable(0.0 , name = 'bias_1')\n", - " pred_y = (W*x) + b\n", - " loss = tf.reduce_mean(tf.square(y - pred_y))\n", - " optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)\n", - " with tf.Session() as sess:\n", - " sess.run(tf.global_variables_initializer())\n", - " \n", - " for epoch in range(n_epochs):\n", - " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n", - " \n", - " if epoch % interval == 0:\n", - " print ('Loss after epoch', epoch, ' is ', curr_loss)\n", - " \n", - " print ('Now testing the model in the test set')\n", - " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n", - " \n", - " print ('The final loss is: ', final_loss)\n", - " plt.plot(test_X[:10], test_Y[:10], 'g', label='True Function')\n", - " plt.plot(test_X[:10], final_preds[:10], 'r', label='Predicted Function')\n", - " plt.legend()\n", - " plt.show()\n", - "pass\n", - "linear_regression()" - ], - "execution_count": 21, - "outputs": [ - { - "output_type": "stream", - "text": [ - "Loss after epoch 0 is 48290.105\n", - "Loss after epoch 50 is 29.782778\n", - "Now testing the model in the test set\n", - "The final loss is: 33.2231\n" - ], - "name": "stdout" - }, - { - "output_type": "display_data", - "data": { - "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAFKCAYAAADMuCxnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XdYk+fbxvFvBgkkgKLi3nuLo63W\nDrXaWqsd1l2tWtx7oqjUvfeuVuuqs2ptta1dSrV2Kq66xYUbUEASEkjyvH+k5fe2tYoKPAGuz3F4\nCCQ8ObnNwWmSJ9etURRFQQghhBCq0qodQAghhBBSyEIIIYRHkEIWQgghPIAUshBCCOEBpJCFEEII\nDyCFLIQQQngAvZo3Hh19L0OPHxBg4u5da4beRnYna5g+ZB3Th6zjk5M1TB+Pu46BgX7/eVm2foSs\n1+vUjpDlyRqmD1nH9CHr+ORkDdNHRqxjti5kIYQQIquQQhZCCCE8gBSyEEII4QGkkIUQQggPIIUs\nhBBCeAApZCGEEMIDSCELIYQQHiBNg0FsNhvNmzenT58+1KtXj9DQUBwOB3q9npkzZxIYGEiVKlWo\nVatW6vesXr0anS7rvd9t4cK5nDlzijt3YrHZbBQuXAR//1xMmTIzXY7fqlUL8ucvgFb7v/8LLVq0\n/ImP++OPP/DMM8+SkBDPypXLCAkZ/cTHFEIIkXnSVMhLly4lV65cAMybN482bdrQrFkz1q9fz6pV\nqwgJCcHX15d169ZlaNjM0L//YAC+/HInFy5E0q/foHS/jVmzFmAymdL1mJs2radWrafImzeflLEQ\nQmRBDy3kyMhIzp8/T4MGDQAYO3YsRqMRgICAAE6cOJGhAT1FRMRBNm36GKvVSr9+gxk6tB9ffPE9\nAGPGhNCyZRsqVqzElCnjuXfvHk6nk0GDhlO2bLk0Hf+111761/EOHz6ExZLIlSuXuXbtKgMGDKVe\nvfrs3v0FW7duRqPR0K7dO6SkpHDy5B8MGzaAkSPDGD9+DCtXriMi4iDLly9Br9cTGJif0ND3+e67\nrzl27AhxcXe5cuUyHTp0onnzNzNs3YQQQqTNQwt5+vTphIWFsWPHDoDUR3ZOp5MNGzbQt29fAJKT\nkxk6dCjXrl3jlVdeoWvXrk8cbtxPY9gZueOxv1+r1eByKX/7WosybzLu2UmPdbzIyPNs3Lgdg8Fw\n38u3bNnIM888S4sWb3Lx4gXmz5/FvHlLHuu2/nL79i1mzVrAL7/8xGefbaNGjSBWr17BmjUbSU5O\nYfLksUybNocVKz5g1qwFxMfHpX7vrFlTmTt3MQUKFGTOnOl8++1uNBoNkZHn+eCDj7h6NYqxY0dJ\nIQshxH38duNXEpLjaFzilUy5vQcW8o4dOwgKCqJYsWJ/+7rT6SQkJIS6detSr149AEJCQnj99dfR\naDR07NiROnXqUK1atQfeeECA6YHzQE0+BrRaTVp/lvv65/ebfAwPHO79Fz8/b0ym/103d24TlStX\nokiRvABoNJrUy4xGL3LnNnHmzAnu3LnD3r3fAGC3J/3rtnQ6LaGhg1NfXw8ICGDBggX3PZ7ZbKRe\nvWcIDPSjQoVS2O1JxMffply5shQtGgjAypUfph43Xz5fdLoU9HotXl5O9HodVau6H6E3aPA8v//+\nO5UrV+app2pTsGBu/Py8SEqyPHQ90rJe4uFkHdOHrOOTkzX8b4qi8HXk10zZP4X9V/Zj8jKRGJqI\nRvPvLkrvdXxgIYeHhxMVFUV4eDg3b97EYDBQsGBBduzYQYkSJejXr1/qddu3b5/6cd26dTl79uxD\nC/lhO2WE1HyfkJrvp+XnuK/AQL/77iiVll2m7t2zYbUmp143Ls6KomhSP1cUJfVjiyUp9fL+/YdS\ntWr1/7wtp9PF1Klz//YacnT0vfsez2Kx4+XlQ3T0Pe7etZCc7CA+3obNlnzf48bEJBIfb8HhcBEb\na8HhcKZeLzY2AZvNwb17NpKTXURH38NqteJ0uh64Hv+1huLRyDqmD1nHJydreH8uxcWXF3YxP2I2\nR6MPA9C4+MsMfyqUmJjEf13/cdfxsXd7mjdvHtu2bWPLli20bt2aPn36EBMTg5eXFwMGDEi93oUL\nFxg6dCiKouBwOIiIiKBcubS9dppVaTQabDYbNpuNs2fPAFC5clX27QsH4OLFC2za9PETHe9+SpQo\nyZUrl7FardjtdgYN6oOiKGg0WpxOZ+r1/P390Wg03Lx5E4AjRyKoWLHSY/ykQgiRfaU4U9hyZiMv\nbHqG977uyLHoI7xe5i2+b/MjG5pvpWaB2pmW5ZH3Q96wYQN2u51OnToBUKZMGcaNG0fBggVp1aoV\nWq2WRo0aUb169YccKWt7881W9OjRmZIlS1OhgrvoWrVqy+TJ4+jTpxsul4tBg4Y90fHux8fHh+Dg\nXgwa1AeAtm07oNFoqFmzFn36BDN69LjU64aEjGH8+NHodDqKFCnKSy+9zDfffPV4P7AQQmQjNoeN\nTafXs+jwPK7cu4xeq6ddxXfoX3Mw5QLKq5JJoyiK8vCrZYyMftpEnpp5crKG6UPWMX3IOj65nL6G\niSmJrD2xiqVHFnLLehOjzsg7ld6lb82BFPMrnubjZMRT1o/8CFkIIYTIauJsd1lxfBkfHlvKXftd\nzF6+9A0aSK+gfhQwFVA7HiCFLIQQIhu7bb3NB0cXseqPFVhSEsltzM3wp0LpVq0nAd551I73N1LI\nQgghsp2r96JYfGQ+60+uxea0kd9UgGF1RtK5Sld8DZ75ti8pZCGEENlGZNw5FkTM5ZOzm3C4HBTz\nK06/moNoX7Ej3npvteM9kBSyEEKILO+PmOPMPzSbzyM/RUGhXO7yDKg1hJblWuOl81I7XppIIQsh\nhMiyfr/5K/MOzeLby18DUC1fDQbVHkazUs3RabPWjoNSyP9w48Z13n23HRUqVATcM7rfeaczL77Y\n8JGPtW3bZuLi4njhhQbs2xdOcHDP+17vr60Tvbwe/r+4CxfOM2fOjH9t2fjii89QrVqN1M/z5s3L\n+PFTHznzP+3evZvatetz7tyZB/4MQgiRWRRFYd/VcOYdmsWB6/sBeLpgXQbXHkaj4k3uO+YyK5BC\nvo/ixUukFl5CQjxdu75D3br1MBof7/WHcuUqUK5chf+8/K+tE9NSyP/F19c3XfZV/qfly5ezbFn9\nh/4MQgiR0VyKi68vfcX8Q7OIuH0IgIbFXmJQ7WHUK1xf5XRPTgr5Ifz9c5E3bz5iY2NZtepD9Hov\nEhLimDBhGjNmTOb69Ws4HA66detF7dpPcfDgbyxYMJs8efKSN28+ChcuQkTEQbZv38KkSTMeuHXi\n/PlL+fzzT/nuu91oNFqef74B7dt35PbtW4SFjcTLy4uyZdM+QebGjeuMGTOClSvd+1QHB3di0qTp\nfPTRcvLlC+TMmVPcunWT99+fRIUKFVm/fg3h4d+j0Wjp1asfp0+f5MyZM4waNZxWrdqm/gzff/8t\nmzevR6fTUaFCJQYNGsbKlcvuu1WkEEI8KYfLwWfnt7MgYg6n7pwEoFmpFgyqPZSg/LVUTpd+PLqQ\nzePGYNz5+NsvotWQ5x/bL9pbvIllXNq3X7xx4zoJCfHkz+9+47i/vz8jRoxm9+4vyJs3H6Gh7xMX\nF8fAgb1Ys2YTy5YtIixsIuXKlWfYsAEULlwk9VhWq+WBWydGR98mPPx7lixZCUDv3sE0bNiY7ds3\n89JLL9OmTXs+/ng158+fffw1+VNycjJz5ixix46t7N79BSaTifDw71m2bDXXr1/j449XM3JkGBs2\nrGXKlJlERBz882ewsnz5Ylat2oDJZCIkZHDqZf/cKlIKWQjxJOxOO5+c2cSCiDlcSriITqOjVfm2\nDKg1hIp5st9sfo8uZLVcuXKZfv16AGAwGBgzZjx6vXupKleuAsAffxzj6NHDHDt2BAC73U5KSgo3\nbtygXDn3o9igoFrY7fbU4166dJHixUtiNHpjNHozbdqcv93uqVMnuHo1iv793a/TWq0Wbt68zqVL\nF2nYsDEANWvW4ZdffvpX5sTExNTMAGXKlKVdu47/+TPWqFETgMDAApw8eYKzZ89QuXJVtFotRYsW\nY+TIsPt+X1TUFYoWLZ66W1XNmrU5e/Y0ANWrBwGQP39+EhP/vTuKEEKkhTXFyscnV7P4yAJuWK5j\n0Bp4t/J79Ks5kJK5SqkdL8N4dCFbxk16pEez/xQY6Medx5g1+v9fQ/4nvd4r9e93332PJk2a/u1y\nrfZ/G2j9c0y4VqtDUVz/ebt6vRf16tUnJGT0376+fv0aNBrtn8e8//ff7zXkmzdv/O1zh8OR+vFf\n+zH/lVOn0+JyPXysuUbz95/L4UjBaDTe95hCCPEoEuzxfPTHhyw7uphYWywmvYleNfrRu0Y/CvkW\nVjtehnvg9oviv1WuXJUff/wBgLt377Bs2WIA8uUL5MqVSyiKwuHDh/72PQ/bOrFChUpERBzCZrOh\nKArz5s3CbrdRvHgJTp92v27y19PDaWEymbl79w6KohAbG8P161f/87oVKlTi+PGjOBwO7tyJJTTU\nvVPVP4u1WLESXL16BavVAsDhwxFUqFA5zZmEEOKfYpJimPLLBGquq8KUXyeQ4nIwpPZwDnU6wYT6\nU3JEGYOHP0L2ZI0aNSYi4nd69XoPp9PJe++5ny7u0aMPY8aMoGDBQqmvO//lYVsnLly4nDZt2tO3\nb3e0Wi0vvNAAo9Gb1q3bExY2kn379lKmTNr3mfb396dOnafp1u1dypYt98CzpAsVKswrrzSjX78e\nKIpCz559AahUqRLdu79L794DUn+Gvn0HMnRofzQaLdWrB1GjRhAHD/76SOsnhBDXE6+x5MgC1p1c\nTZIjiXw++RhYdxxdq3bDz+CvdrxMJ9svigeSNUwfso7pQ9bxyXnCGl6Ij2Tx4flsOr2eFFcKRXyL\n0jdoAB0qvYvJy6RqtrSS7ReFEEJkWadiTzI/YjY7zm/DpbgonasMA2oNoVX5thh0BrXjqU4KWQgh\nRIZwKS7+iDlGeNQe9lz5jp+u/whA5bxVGVRrKC3KvJnlxltmJClkIYQQ6eam5QbhUXsIj/qeH6L2\nEmuLTb3s6YJ16V9rMC+XaJplx1tmJClkIYQQjy3JkcTP1w8QHrWHH6L2pE7SAihoLkS7iu/QoFgj\nXijakHw++VRM6vmkkIUQQqSZoiicjD2R+ij4lxs/YXe6ByD56H1oVLwxDYo1okGxl6gQUFEeCT8C\nKWQhhBAPdNt6m31X9/5Zwnu4bb2VelmVvNX+LOBGPFOoHt76x9uER0ghCyGE+Ae7085vN35hb9T3\nhEft4Y+YY6mX5fMJpFX5tjQo1ogXizakgLmgikmzFylkIYTI4RRF4ezdM4T/WcA/Xf+RJEcSAAat\ngeeLNqBBsUY0LPYSlfNWQauRIY8ZQQpZCCFyoDu2WPZFhac+DX3dci31sgoBFWlQ/CUaFmtE3UL1\ns8ywjqxOClkIIXKAZGcyh279zm/Hf+TLM19x5PZhFNyDGvN45+Gtsm/ToNhLvFisIYV9izzkaCIj\nSCELIUQ2pCgKF+Mj2fvn25H2X9uHJcW9Lapeq6de4fqpJ2NVDwySp6E9gBSyEEJkE/H2OPZf3cfe\nqO/5IWoPV+5dTr2sTO6yNCjWiDertqCKuRa+hv+eqSzUIYUshBBZlMPl4PDtQ+y94j4ZK+L2QVx/\n7pmey5ibFmXeTD0burh/CcAzNpcQ9yeFLIQQWUiSI4nPz3/K7ktfsv/qDyQkxwOg0+ioU+Dp1Keh\ng/LXQq+VX/FZifxrCSFEFnAh7jyrT3zEptMfE2ePA6C4f0neKteKBsUa8VyR58llzK1ySvEkpJCF\nEMJDOVwOvr70Fav/WMEPV/cC7sEcg2oNo13FDpTOXVblhCI9SSELIYSHuWm5wccn17Du5GpuWK4D\nUK9wfbpUCea10q/L3sHZlBSyEEJ4AEVR+PHaPlb9sYKvLu7CqTjx9fLjvard6VwlmEp5K6sdUWQw\nKWQhhFBRnO0um89sYM2Jjzgfdw5wb9jQtWo3WpZvja+Xr8oJRWaRQhZCCBUcuR3B6j9W8un5rSQ5\nkjBoDbQu344uVYOpU+Bp2bYwB5JCFkKITGJNsfLZ+e2sPrGCw7cjACjhX5LOVYJpX7EjeX3yqpxQ\nqEkKWQghMtj5u+dYc2Ilm85sIN4eh1ajpWnJZnSp2o0GxRrJ2EoBSCELIUSGSHGmsPvSl6w+sZL9\nV8MBCPTJz+Daw+hUuStF/YqpG1B4HClkIYRIRzcSr7Pu5Go+PrWGm5YbANQv/Dxdqgbzaqnm8pYl\n8Z+kkIUQ4gm5FBf7r/7A6hMr2X3xC5yKEz+DP92q9aRzlWAq5KmodkSRBUghCyHEY7pru8Om0xtY\nc2IlF+IjAaiWrwZdqgbTslxrzF5mlROKrEQKWQghHoGiKBy+fYjVJ1ay49w2bE4bRp2RNhXa07Vq\nN2rlryNvWRKPRQpZCCHSwJpi5dNzW1l1YgXHoo8AUCpXaTpXCaZdxQ7k8Za3LIknI4UshBAPcO7u\nWfdblk5vICE5Hq1Gy6ulmtOlSjAvFmsob1kS6UYKWQgh/iHFmcJXF3ex+sRKfry2D4D8pgJ0q96T\nTpW6UMSvqMoJRXYkhSyEEH+6nniNtSdXsf7kWm5ZbwLwXJEX6Fq1G01LvoaXzkvlhCI7k0IWQuRo\nLsXFD1F7WX1iJV9f+hKX4sLfkIse1XvTuUow5QLKqx1R5BBSyEKIHOuu7Q5td77FkejDANQIrEmX\nKsG8We5tecuSyHRSyEKIHMmaYqXTl+04En2YZqVaMLDWEGoWqK12LJGDSSELIXIch8tBj2+68NvN\nX2hZrhVLGq+Qs6WF6uQeKITIURRFYWj4AL65vJsXizZkQaMPpIyFR5B7oRAiR5n8y3g2nv6YoMCa\nrGr6sWz2IDyGFLIQIsdYdnQxCw7PoXSuMmxovg1fg5/akYRIJYUshMgRtp3dQtiBUAqYCrKlxQ7y\n+eRTO5IQfyOFLITI9vZe+Z7+e3rhb8jFpubbKe5fQu1IIgvQ3L2D9vKlTLs9KWQhRLYWcesgXXd3\nRKfRsa7ZJqrkq6p2JOHhNAnxmKZNIk+tquR5sS4oSqbcbpoK2Waz0bhxY7Zv386NGzfo0qULHTt2\npEuXLkRHRwPw+eef8/bbb9O6dWs++eSTDA0thBBpcf7uOd75ojU2ZxLLmqyiXuH6akcSnsxiwWfB\nXPLUqYZ5zgwwmbg3bTZk0naaaSrkpUuXkitXLgDmzZtHmzZt+Pjjj2nSpAmrVq3CarWyePFiVq9e\nzbp161izZg1xcXEZGlwIIR7kpuUGbXe9RawtllkvzqdZ6eZqRxKeym7He+Uy8j5dA99JYwFIHDOO\n2N+OYm/3TqbFeOhgkMjISM6fP0+DBg0AGDt2LEajEYCAgABOnDjB0aNHqVatGn5+7jMWa9WqRURE\nBI0aNcq45EII8R/i7XG03fkWUfeuEPp0GB0rd1Y7kvBEDgfGTzZhnjkV3dUoFJMZy5DhJPXuj5Ir\nd6bHeegj5OnTpzNy5MjUz00mEzqdDqfTyYYNG2jRogUxMTHkyZMn9Tp58uRJfSpbCCEyU5IjiY5f\ntuXUnZMEV+vBoNrD1I4kPI3LhfGz7QS88Az+A/ugjb6NtWdfYn8/hnVkmCplDA95hLxjxw6CgoIo\nVqzY377udDoJCQmhbt261KtXj507d/7tciWNL4AHBJjQ63WPGPnRBAbK+wyflKxh+pB1TB8PWkeH\ny0G3LR359cbPtKnShuVvLZUpXPeRY++LigJffgmjR8PRo6DXQ48eaMLCMBUtiukRD5fe6/jAQg4P\nDycqKorw8HBu3ryJwWCgYMGC7NixgxIlStCvXz8A8ufPT0xMTOr33b59m6CgoIfe+N271ieM/2CB\ngX5ER9/L0NvI7mQN04esY/p40DoqisKQ8P58fuZzni/agNnPLSY2xpLJCT1fTr0veh3Yj3nyeLwO\n/oai0WBv1RbL8FBcpUq7r/CIa/K46/igEn9gIc+bNy/144ULF1KkSBFiYmLw8vJiwIABqZfVqFGD\nMWPGkJCQgE6nIyIiglGjRj1yUCGEeFzTfpvI+lNrqRFYkzVN12PUGdWOJDyAPuIg5ikTMezbC4C9\nWQssI0bjrFRZ5WT/9si7PW3YsAG73U6nTp0AKFOmDOPGjWPo0KEEBwej0Wjo27dv6gleQgiR0VYc\n+4C5h2ZRKldpNry2VUZiCnQnT2CeNgnj7i8ASG7QCEtoGI6anrvFpkZJ6wu+GSCjnzbJqU/NpCdZ\nw/Qh65g+7reOn57bSq9vgwk05eeLlt9Swr+kOuGyiOx+X9ReiMQ8YwrGT7eiURRSnq6LZdT7pDz7\nXLreTqY/ZS2EEJ4sPGoP/b7via/Bj03Nt0sZ52Daa1cxzZmB94Z1aJxOUqrVwBo6huSXXs60wR5P\nSgpZCJElHbkdQdfdHdFqtKx7dRNV81VTO5JQgSY6GtOC2fisXonGbsdRrjyWEaNJbv4GaLPWGfZS\nyEKILOdC3Hk6fNGKJIeVFS+v5dki6ft0pPB8mvg4fJYswLRsKRqrBWex4liGh2Jv1db9dqYsKGum\nFkLkWLcsN2mz8y1ikmKY+eI8mpd5Xe1IIjNZLPis+ADTovlo4+Nw5i+ANWw8to6dwZi1z6yXQhZC\nZBlxtjja7mrJlXuXCXlqFJ2rvKd2JJFZ7HZ81n6Eae4stDHRuAICSAybQFJwDzA96kgPzySFLITI\nEmwOG602teJk7B90rdqNoXVGqB1JZAaHA+/NGzDNmobu2lVcZl8sQ0eQ1Lsfin8utdOlKylkIYTH\nc7qc9Po2mH2X99GizJtMeW4mmixy5qx4TH/OmzZNn4z+QiSKtzfWPgOw9h+Mkjev2ukyhBSyEMKj\nKYpCyL4hfHlxJ41KNWJJ4w/RaTN2Br5QkaJg+GY35qkT0Z/8A0WvJ6lzMNYhw3EVKqx2ugwlhSyE\n8GjTf5/MupOrqJqvOp+2/RR7gjwyzq689v+Aecp4vA4dRNFosLVu5543XbKU2tEyhRSyEMJjrTy+\nnDkHZ1DCvyQbm2/D3+hPNNl3ylROpT/4G+apEzHs/wEA+2uvu+dNV6ykcrLMJYUshPBIn53fzqj9\nw8nnE8iWFjsoYCqgdiSRznQn/sA8bSLGr78CILnhS+5500G1VE6mDilkIYTH2Xc1nD7fdcfs5cvm\n5tsplau02pFEOtJFnsM0Ywren24DIOWZeu550/Xqq5xMXVLIQgiPciz6CJ2/6oAGDWte3UC1wBpq\nRxLpRHs1CtPs6XhvWu+eN109CMuoMFIaNs4y86YzkhSyEMJjXIiPpN2ut7GmWFjxyhqeL/qi2pFE\nOtDcvo1p/ix81nyEJjkZR/kKWEaMIbn561LE/48UshDCI9yy3qLtzreISYpm+gtzaFHmTbUjiSek\nibuLafECfD5cisZqxVm8xP/mTevkrWv/JIUshFBdgj2edjtbcjnhEkPrjKBr1W5qRxJPIjER04dL\n8Vm8AG1CPM4CBbG+P9E9b9pgUDudx5JCFkKoyuaw0fmrDpyIPc67ld8j5KlRakcSj8tmw2fNSkzz\nZ6ONiXHPmx47iaSu3bLNvOmMJIUshFCN0+Wkz3fdOXB9P6+Vfp3pL8yWkZhZUUoK3pvWY5o9Hd31\na7h8/bAMDyWpV18UP3+102UZUshCCFUoisLI/cPYdeEzni38HEsbr5CRmFmNy4Xx062YZkxBf/GC\ne95034FY+w9CyZM9501nJClkIYQqZh2cxpoTK6mStxprX92It95b7UgirRQFw+4vMU+bhP7UCRQv\nL5K6dsM6eDiugoXUTpdlSSELITLd6j9WMvP3qRT3L8mm5tvwN2avbfSyLUXBa1845qkT8Io4hKLV\nYmvbAcuwkbhKlFQ7XZYnhSyEyFQ7I3cwYt8Q8vnkY0vz7RQwF1Q7kkgD/W+/Yp46AcOB/QDYW7zp\nnjddvoLKybIPKWQhRKb58do+en/bDZOXmY2vbaN07rJqRxIPoTt+zD1v+tuvAbC/1ARraBiO6kEq\nJ8t+pJCFEJniePRR3v2yPQoKq5uup0b+mmpHEg+gO38O0/TJeH+2HYDkevWxhL6Po249lZNlX1LI\nQogMdzH+Au12vY0lJZHlL6/ixWIN1Y4k/oM26gqmWdPw3rwBjctFSo2a7o0fGjSSMZcZTApZCJGh\nbltv03bnW0Qn3Wbq8zN5o2xLtSOJ+9DcuoV53ky8165Ck5KCo0JFLCPDSG7WXIo4k0ghCyEyzL3k\nBNrveptLCRcZUns4wdV6qh1J/IPm7h1Mi+bjs+IDNElJOEuUxBIyCnvL1jJvOpNJIQshMoTdaafL\nV+9wPOYonSp3YcTTY9SOJP4fTeI9fJYtwWfJQrT3EnAWKox1wlRsHTqBl5fa8XIkKWQhRLr7ayTm\n/ms/8Gqp5kx/YY6MxPQUSUn4LF2EacFstLGxuPLmJXH8FJK6BIOPj9rpcjQpZCFEulIUhVE/Dmdn\n5A7qFnqWD5qsRK+VXzWqS0nBe8M6mDcT32vXcPn5YxkxmqSefVB8/dROJ5BCFkKkszmHZrDqjxVU\nylOFdc024aOXR12qcjoxbv8E84wp6C5fAh8frP0HY+03ECUgj9rpxP8jhSyEeCiny4ndaSfZacf+\nrz82kp3J2Bw2jtyOYPpvkynuV4LNLbaTy5hb7eg5l6Jg+HIX5umT0J8+5Z43HdwDn4njsOh91U4n\n7kMKWQgP9lcRppbe3/62Y3f8rxiTnfbUy+1OG3ZnMnaHDbvrr+v9+bU/v9f2V8E+7BhOGw6XI82Z\n83rnZXOL7RQ0yyYDqlAUvML3uOdNHzmMotWS1L4j1qEjcBUvgU+gH0TfUzuluA8pZCE80K83fqHn\nN125brmWKbfnpfXCoDPirTNi0Bkx6oz4G/wx6r0xaA14670x6AwYdd4Y//z7b9fXGzFqjRj13rxa\n6jVK5SqdKbnF3+l/+dk9b/rnAwDY3miJNWQUznLlVU4m0kIKWQgP88WFnfT+NpgUVwr1Cz//Zxn+\n/7L8sxT/LElvnfefBen+2KAzpH6P8f/9cR/jz2LVe2PU/vm3zohWo1X7xxZPQH/8KKapEzF+9w0A\n9iavYBkZhrNadZWTiUchhSwnjy/jAAAgAElEQVSEB1l5fDmj9g/HR29i/WvraVS8idqRhAfTnTvr\nnjf9+acAJNd/3j1v+ulnVE4mHocUshAewKW4mPzLeBYenks+n0A2vrZVNl8Q/0l75TLmWdMwbtno\nnjddsxaWUWNJeaGBjLnMwqSQhVBZsjOZQXv7svXsZkrnKsOm5tspmauU2rGEB9Leuolp7ky81612\nz5uuVNk9b7ppMynibEAKWQgV3UtOoOvuTuy7upfaBZ7i42ZbyOuTV+1YwsNo7sS6502vXOaeN12y\nlHve9FutZN50NiKFLIRKblpu0H5XK07EHqdpyWZ80OQjTF4mtWMJD6K5l+CeN710kXvedOEiWCeN\nwNbuHZk3nQ1JIQuhgrN3ztBuV0uuJkbRuUowU5+fKeMlxf8kJeGzaoV73vSdO7jy5SMxZCpJnYPB\n21vtdCKDyG8AITLZLzd+5t0v2xJnj2PUM+8zsNZQ2XhBuCUn471+Laa5M9HdvIHLPxeW0DCs3XuD\nr0zXyu6kkIXIRLsiP6f3d8E4FScLGi2lXcV31I4kPIHTiXHrZswzp6G7cgnFZMI6cCjWvgNQcgeo\nnU5kEilkITLJimMfMPrHEZi8zKx9ZRMNi7+kdiShNkXBsOtzzDMmoz9zGsVgwNq9F9aBw1Dy51c7\nnchkUshCZDCX4iLk2xBm/jSTQJ/8bGy+leqBQWrHEmpSFLz2fod56iS8jh5G0elIeudd97zposXU\nTidUIoUsRAZKdiYzYE9vtp/7hLK5y7Gx+TZK+JdUO5ZQkdcvP2GaMgHDLz8BYHvrbfe86TLlVE4m\n1CaFLEQGSbDH0/XrTuy/Gk69ovVY9fIG8njLe4xzKv3Rw5inTsSw5zsA7K+8imXEGJxVq6mcTHgK\nKWQhMsCNxOu0/6IVJ2P/4NVSzdnWfguJcWnfwlBkH7ozpzFPn4xx12cAJD//IpbQMBx1nlY5mfA0\nUshCpLMzd07TbldLriVepWvVbkx5biY+Xj4kInvQ5iTaSxfd86a3bnbPm65dB0vo++5500LchxSy\nEOnol+s/0emrdsTb4xhTdxz9aw6W9xjnMNqbNzDNmYH3x2vQOBw4KlXBMup9kl9uKvOmxQNJIQuR\nTnZG7qDPd91xKk4WvbSMNhXaqx1JZCJNbCymhXPx+Wg5GpsNR+kyWEeMxv5GS9DKftPi4aSQhUgH\ny48uIexAKCYvM+uabqZBsUZqRxKZRJMQj8/SRfgsW4I28R7OIkWxDhuJrW0H0MuvWJF2cm8R4gm4\nFBcTfn6fJUcWkN9UgI3Nt1EtX3W1Y4nMYLXis3I5pkVz0d69iytfIImhY0jq1FXmTYvHIoUsxGOy\nO+0M+L4Xn57fRrnc5dnYfBvF/UuoHUtktORkvD9eg2nODHS3b+HKlZvE0WNJCu4p86bFE5FCFuIx\nxNvj6Lq7Iz9e28fTBeuyrtkmArzzqB1LZCSnE+MnmzDPmobuymUUkxnL4GEk9RmAkiu32ulENiCF\nLMQjup54jfa73ubUnZM0K9WCpU1W4KP3UTuWyCguF4YvPsc8bRL6c2fd86Z79sE6YChKYKDa6UQ2\nkqZT/2w2G40bN2b79u0ArF27lipVqmCxWFKvU6VKFTp16pT6x+l0ZkxiIVR0+s4pmm1rzKk7Jwmu\n1oOVr6yVMs6uFAXD99+Qu8mL5Ap+F92FSJI6deHOr0ewTJwmZSzSXZoeIS9dupRcuXIBsGPHDmJj\nY8n/j51IfH19WbduXfonFMJD/HTtRzrv7kC8PY6wehPoFzRQ3mOcTXn9fADz5PF4/fYLikaDrWVr\nrCGhOEuXVTuayMYeWsiRkZGcP3+eBg0aANC4cWN8fX3ZuXNnRmcTwmN8dn47fb/rgYLCksYf0qp8\nW7UjiQygPxKBecoEDOF7ALA3fQ3LyDE4K1dRN5jIER76lPX06dMZOXJk6ue+/3EWYXJyMkOHDqVd\nu3asWrUq/RIKobIPji6i+zddMOiMbGy+Tco4G9KdPoV/l3cIeLkBhvA9JL/QkLtffU/C2o1SxiLT\nPPAR8o4dOwgKCqJYsYfvzxkSEsLrr7+ORqOhY8eO1KlTh2rVHryLSUCACb1e92iJH1FgoF+GHj8n\nyKlr6FJcDP9mOHN+mUMh30J89c5X1ChY47GPl1PXMb2l6zpGRsK4cbB+PSgK1KsHkydjaNgQQ/rd\niseR+2L6SO91fGAhh4eHExUVRXh4ODdv3sRgMFCwYEGeffbZf123ffv/jQmsW7cuZ8+efWgh371r\nfczYaRMY6Ed0tAz0fxI5dQ3tTjv9v+/JjvPbKR9QgY3Nt1FYV/yx1yKnrmN6S6911N64jmn2DLw3\nrHXPm65SDcuoMJIbv+KeN52N/63kvpg+HncdH1TiDyzkefPmpX68cOFCihQpct8yvnDhAosXL2bW\nrFk4nU4iIiJo2rTpIwcVwhPE2+Po/FUHfrr+I88UqsfaVzfKe4yzCU1MDKYFc/BZ9SEaux1HmbJY\nR47B3uJNmTctVPfI70NeunQpP/30E9HR0XTv3p2goCBCQkIoWLAgrVq1QqvV0qhRI6pXl/GBIuu5\ndu8q7b94m9N3TtG89Bssafwh3noZg5jVaRLi8Vmy0D1v2pKIs2gxLMNDsbduJ/OmhcfQKIqiqHXj\nGf20iTw18+Ry0hqejD1B+11vc8Nyne7VejGh/lR02vQ5xyEnrWNGeuR1tFj+N286Lg5XYH4sg4dh\n69QVjMaMC+rB5L6YPjL9KWshcooD1/bT+asOJCTHM7beJPoE9Zf3GGdldjveH6/GPGcm2ujbuHLn\nJnHMOPe8abNZ7XRC3JcUssjxPj23lf7f90JBYWnjFbxdvo3akcTjcjjc86ZnTkV3Nco9b3rIcJJ6\n95d508LjSSGLHG3pkUWM/WkUfgZ/Vjddz/NFX1Q7kngcLhfGnTswTZ+M/vw5FKMRa8++WAcMkRGX\nIsuQQhY5kktxMfbAKJYdW0JBcyE2vraNKvmqqh1LPCpFwfDd15inTER/4jiKXk9Sp65Yh4bgKlxE\n7XRCPBIpZJHj2Bw2+n/fi88it1MhoCIbm2+jqN/Dh98Iz+J1YL973vTB39zzplu1xTI8FFep0mpH\nE+KxSCGLHCXOdpfOuzvw8/UD1CtcnzVNN5DbO0DtWOIR6CMOYp4yEcO+vQDYm7XAMmI0zkqVVU4m\nxJORQhY5xrV7V2m3qyVn7p7m9TJvseilZfIe4yxEd/IEzJ1GwGefAZDcoBGW0DAcNWurnEyI9CGF\nLHKEEzF/0P6Lt7lpuUHP6n0YX38KWo1MZsoKtBciMc+YgvHTraAopDxdF8uo90l59jm1owmRrqSQ\nRbYWb49jxfFlLD68gMSUe4x/dgq9g/qpHUukgfbaVUxzZuC9YR0ap5OUqtXxmj6VuDrPuedNC5HN\nSCGLbOmu7Q7Lji1hxbFlJCTHE2AMYHmTVbxZ7m21o4mH0ERHY1owG5/VK93zpsuWwzJyDMnN3yCw\nQK5svfGDyNmkkEW2EpMUwwdHFrHyj+VYUhLJ55OPsHoT6FolGF+DbDnnyTTxcfgsWYBp2VI0VgvO\nYsXd86ZbtZV50yJHkHu5yBZuWW6y+MgC1p74CKvDSn5TAUY8PYpOlbti9pJRiR7NYsFnxQeYFs1H\nGx+HM38BrGHjsXXsnGPnTYucSQpZZGnXE6+x6PA81p1cjd1pp7C5CGH1xtOh0rv46H3UjicexG7H\nZ+1HmObOQhsT7Z43HTaBpOAeYDKpnU6ITCeFLLKkKwmXWRAxl02nPybZlUxxvxIMqDWEthU7YNTJ\noyqP5nDgvXkDplnT0F27isvsi2XoCJJ690Pxz6V2OiFUI4UsspQL8ZEsODSHLWc34nA5KJWrNINq\nDaNV+bZ46bzUjicexOXC+Nl297zpC5Eo3t5Ye/fH2n8wSr58aqcTQnVSyCJLOHf3LPMOzWLbuS24\nFBflcpdnUO1hvFWuFXqt3I09mqJg+GY35qkT0Z/8wz1vunMw1iHDcRUqrHY6ITyG/CYTHu1U7Enm\nHprBZ+c/RUGhUp7KDKkTQvPSb6DT6tSOJx7Ca/8PmKeMx+vQQfe86dbt3POmS5ZSO5oQHkcKWXik\n49FHmXNoJl9c+ByAavlqMKROCK+Wek0mbGUB+oO/YZ46EcP+HwCwv/a6e950xUoqJxPCc0khC48S\ncesgcw7O4JvLuwGolb82Q+qE0KREUzQyncnj6U78gXnaRIxffwVAcsOX3POmg2qpnEwIzyeFLDzC\nrzd+Yc7B6eyN+h6ApwvWZWidETQo1kiKOAvQRZ7DNGMK3p9uAyDlmXruedP16qucTIisQwpZqEZR\nFH66/iNzDs5g/zX3U5vPFXmBIXVCqF/4eSniLEB7NQrT7Ol4b1rvnjddrQbWUWEkN2oi86aFeERS\nyCLTKYrCD1f3MvvgdH698TMADYo1YkidEdQtVE/ldCItNLdvY5o/C581H6FJTsZRrrx73vRrr4NW\nXuMX4nFIIYtMoygK313+mjmHZnDo1kEAXi7RlMF1hlO7wFMqpxNpoYm7i2nxAnw+XIrGasVZvASW\nYSOxt24HOjnrXYgnIYUsMpxLcbH74pfMOTSDY9FHAGhWqgVD6gynemCQyulEmiQmYvpwKT6LF6BN\niMdZoCDW9ye6500bDGqnEyJbkEIWGcbpcrLrwmfMOTiTU3dOoEHDG2VaMrjOcCrnraJ2PJEWNhs+\na1Zimj8bbUwMroAAEt+fSNJ73WXetBDpTApZpDuHy8GO89uYd2gWZ++eQavR0qp8WwbVGkb5PBXU\njifSIiUF703rMc2eju76NVy+fliGh5LUqy+Kn7/a6YTIlqSQRbpJcaaw7dwW5h6aycX4C+i1etpX\n7MjAWkMonbus2vFEWrhcGD/dinn6ZHSXLrrnTfcdiLX/IJQ8edVOJ0S2JoUsnliyM5lNp9ezIGIO\nV+5dxkvrRafKXRlQazAl/EuqHU+khaJg2P0l5mmT0J86geLlRVLXblgHD8dVsJDa6YTIEaSQxWOz\nOWysP7WWRYfncS3xKkadkeBqPegXNIgifkXVjifSQlHw2heOeeoEvCIOoWi12Np2wDJsJK4SJdVO\nJ0SOIoUsHpk1xcq6k6tYdHg+t6w38dH70LNGX/oFDaSAuaDa8UQa6X/7FfPUCRgO7AfA3uJN97zp\n8vI6vxBqkEIWj2RX5OeE7BtMTFI0Jr2Z/jUH06tGPwJNgWpHE2mkO37MPW/6268BsL/UBGtoGI7q\n8hY0IdQkhSzSJMmRxPsHRrHmxEp89D4MqT2cHjX6kMdbTvTJKnTnz2GaPhnvz7YDkFyvPpbQ93HU\nleloQngCKWTxUKfvnKLnN105decklfJUZvnLq6mQp6LasUQaaaOuYJo1De/NG9C4XKTUqOne+KFB\nI5k3LYQHkUIW/0lRFD489CEDdw8kyZFElyrBjK8/BR+9j9rRRBpobt3CPG8m3mtXoUlJwVGhIpaR\nYSQ3ay5FLIQHkkIW9xVvj2No+EA+j/yUXMbcLH7pQ5qXeV3tWCINNHfvYFo0H58VH6BJSsJZoiSW\nkFHYW7aWedNCeDApZPEvB2/+Rq9vg7ly7zL1i9VnQYNlFPMrrnYs8RCaxHv4LFuCz5KFaO8l4CxU\nGOuEqdg6dAIvL7XjCSEeQgpZpHIpLhYdnsfUXyfiUlwMqRPC9Fcnczc2Se1o4kGSkvBZvRLTgtlo\nY2Nx5c1L4vgpJHUJBh95eUGIrEIKWQBwy3qLvt/1YN/VvRQ0F2JJ4w95rsgL6LVyF/FYKSl4b1iH\nac4MdDeu4/LzxzJiNEk9+6D4+qmdTgjxiOS3rWDPlW/p931PYpJieLlEU+Y3WkpeH3k7k8dyOjFu\n/wTzjCnoLl9C8fHB2n8w1n4DUQLyqJ1OCPGYpJBzsGRnMlN+ncCSIwswaA1Mqj+N7tV7o5EzcD2T\nomD4chfm6ZPQnz7lnjcd3AProGG4CsiENCGyOinkHOpi/AV6ffseh29HUDpXGZa/vIrqgTKpySMp\nCl7he9zzpo8cRtFqSWrfEevQEbiKl1A7nRAinUgh50Dbz33CsPBBJKbco02F9kx7fha+BnnN0RPp\nf/nZPW/65wMA2N5oiTVkFM5y5VVOJoRIb1LIOYglxcKo/cPZePpjzF6+LH5pOa0rtFM7lrgP/fGj\nmKZOxPjdNwDYm7yCZWQYzmrVVU4mhMgoUsg5xPGYY/T8pivn485RPTCI5U0+onTusmrHEv+gO3sG\n8/TJGHfuACC5/vPuedNPP6NyMiFERpNCzuYUReGjP5Yz9sBokl3J9KzRlzF1x2HUGdWOJv4f7ZXL\nmGdNw7hlo3vedM1aWEaNJeWFBjLmUogcQgo5G7tji2XQ3n7svvgFeb3zsvClD2hc4hW1Y4n/R3vr\nJqa5M/Fet9o9b7pSZfe86abNpIiFyGGkkLOpn68foPe33bhuucZzRV5gSeMPKWgupHYs8SfNnVj3\nvOmVy9AkJeEoVRpryCjsb74t86aFyKGkkLMZp8vJnEMzmH1wOho0hD4dxoBaQ9Bp5Ze8J9DcS3DP\nm166yD1vunARrJNGYGv3jsybFiKHk0LORq4nXqP3d934+foBivoW44MmH/F0ITkZyCMkJeGzZKF7\n3vSdO7jy5SMxZCpJnYPB21vtdEIIDyCFnE3svvglA/f05q79Ls1Lv8GcBgvI7R2gdiyRnIz3+rUw\nfxa+16/j8s+FJTQMa/fe4OurdjohhAeRQs7ibA4bE34OY8XxZXjrvJnxwlw6V3lPxl+qzenEuHUz\n5pnT0F25BCYT1oFDsfYdgJJb/qMkhPg3KeQs7Pzdc3T/pgsnYo9TIaAiy19eTaW8ldWOlbMpCoZd\nn2OeMRn9mdMoBgPW7r0wTRyHRWtSO50QwoNJIWdBiqKw6fR6QvcPw+qw0qlyVybWn4rJS37hq0ZR\n8Nr7Heapk/A6ehhFpyPpnXfd86aLFsMU6AfR99ROKYTwYFLIWcy95ASG/zCY7ec+wd+QixUvr+H1\nsm+pHStH8/rlJ0xTJmD45ScAbG+97Z43XaacysmEEFmJFHIWcvjWIXp++x6XEi5Su8BTLGvyEcX9\nZbcfteiPHsY8dSKGPd8BYH/lVSwjxuCsWk3lZEKIrEgKOQtwKS6WHlnE5F/H4XQ5GVhrKCFPjcJL\nJ+9bVYPuzGn3vOldnwGQ/PyLWELDcNR5WuVkQoisTJuWK9lsNho3bsz27dsBWLt2LVWqVMFisaRe\n5/PPP+ftt9+mdevWfPLJJxmTNgeKtkbT4YtWjP95DHm887KlxQ5G1x0rZawC7aWL+PXrScCLdTHu\n+oyU2nWI2/o58dt2ShkLIZ5Ymh4hL126lFy5cgGwY8cOYmNjyZ8/f+rlVquVxYsXs3XrVry8vGjV\nqhVNmjQhd+7cGZM6h/ghai99v+/BbestGhVvzMJGywg0BaodK8fR3ryBac4MvD9eg8bhwFGpCpZR\n75P8clOZNy2ESDcPLeTIyEjOnz9PgwYNAGjcuDG+vr7s3Lkz9TpHjx6lWrVq+Pm5N7mvVasWERER\nNGrUKGNSZ3MpzhSm/zaZhYfnotfqGffsZHrV6ItWk6YnNEQ60cTGYlo4F5+PlqOx2XCULoN1xGjs\nb7QErfxbCCHS10MLefr06YSFhbFjh3t/Vt/7TBeKiYkhT548qZ/nyZOH6OjodIyZc1xJuEzPb9/j\n0K3fKelfiuUvryIofy21Y+UomoR4fJYuwmfZErSJ93AWKYp12EhsbTuAXk67EEJkjAf+dtmxYwdB\nQUEUK1bskQ6qKEqarhcQYEKvz9hNDwID/TL0+OnpkxOf0H1nd+Lt8XSo1oGlry3F3+ivdqwstYZP\nxGqFRYtg+nS4cwfy54fJk9D16IGftzdPugo5Zh0zmKzjk5M1TB/pvY4PLOTw8HCioqIIDw/n5s2b\nGAwGChYsyLPPPvu36+XPn5+YmJjUz2/fvk1QUNBDb/zuXetjxk6bwEA/orPAMAZripWwAyNZd3I1\nJr2JBY2W0rZCB+wJGqJRN39WWcMnkpyM97rVmObORHf7Fq5cubGOHktScE/3vOl7Ke4/TyBHrGMm\nkHV8crKG6eNx1/FBJf7AQp43b17qxwsXLqRIkSL/KmOAGjVqMGbMGBISEtDpdERERDBq1KhHDpoT\nnYo9SY9vunDm7mmq5qvO8iarKBsgAyUyhcPhnjc9axq6K5dRTGYsg4eR1GcASi45IVEIkbke+QWx\npUuX8tNPPxEdHU337t0JCgoiJCSEoUOHEhwcjEajoW/fvqkneIl/UxSF327+ypYzG/jkzCZsThvd\nq/UirN4EvPWyFV+Gc7kwfPE55mmT0J8765433bMP1gFDUQLlLHYhhDo0Slpf8M0AGf20iac9NRN1\n7wpbzmxky5mNXIy/AEBhcxGmvTCbpqWaqZzu/jxtDZ+IomDY8y2mKRPxOn4URafD1qET1iEhuIoU\nzdCbzlbrqCJZxycna5g+Mv0pa/HkElMS2RX5GVvObOTHa/sA8NH78Ha5NrSt2IHni7yITpuxJ7YJ\n8Pr5AObJ4/H67RcUjQZby9ZYQ0Jxli6rdjQhhACkkDOES3Fx4Np+Np/ZwK7Iz7E63BPN6hWuT9sK\nHWhR5g38DOqfPZ0T6I9EYJ4yAUP4HgDsTV/DMnIMzspV1A0mhBD/IIWcji7EnWfzmQ18cmYzVxOj\nACjuX5K2FQbQunw7SuYqpXLCnEN3+hTmaZMwfukeYJP8QkMsoWNw1H5K5WRCCHF/UshPKN4ex47z\n29l8egMHb/0GgK+XHx0qdqJtxQ48U6ieTNjKRNqLFzDPnIpx2xY0ikJKnaexjHqflOdeUDuaEEI8\nkBTyY3C4HPwQtYdNpzew+9IX2J12NGh4sWhD2lbsQLNSLTB5mdSOmaNob1zHNHsG3hvWuudNV6mG\nZVQYyY1fkXnTQogsQQr5EZyKPcnmMxvYenYzt623ACiXuzxtK3agVfm2FPYtonLCnEcTE4NpwRx8\nVn2Ixm7HUaYs1pFjsLd4U+ZNCyGyFCnkh4hNimX7uS1sPrORY9FHAMhtzE3Xqt1oW6EDNfPXRiOP\nwDKdJiEenyUL3fOmLYk4ixbDMjwUe+t2Mm9aCJElyW+u+0h2JvPd5W/YdGY9313+GofLgU6j4+US\nTWlbsQMvl3wVo86odsycyWLBZ+VyTIvmoo2LwxWYn3tjxmLr2AWM8m8ihMi6pJD/pCgKx6KPsPnM\nBraf+4Q7tjsAVMlbjbYV29OyXBvym/I/5Cgiw9jteH+8GvOcmWijb+PKnZvEMeNJCu4BZrPa6YQQ\n4onl+EK+ZbnJJ2c3s+XMBk7fOQVAPp9AetboS9sKHaiar5rKCXM4hwPjJ5swz5yK7moULrMvliEh\nJPXuJ/OmhRDZSo4s5CRHErsvfsHmMxsIj9qDS3Fh0BpoXvoN2lXsQMNijfHSeakdM2dzuTDu3IFp\n+mT058+hGI1Ye/XDOmAISr58aqcTQoh0l2MK+f9v6PDZ+U9JSI4HoFb+2rSp2IG3yr5NgHcelVMK\nFAXDd19jnjIR/YnjKHo9SZ26Yh0agquwnMUuhMi+sn0hR927widnNrHlzEYuxEcCUMhcmC5VgmlT\noT3l81RQOaH4i9eB/e550wd/c8+bbtUWy/BQXKVKqx1NCCEyXLYs5L82dPj0yy3svbQXkA0dPJk+\n4iDmKRMx7HP/W9mbtcAyYjTOSpVVTiaEEJkn2xSyoigcuL6fTafX/21Dh7qFnqVdxXdkQwcPpDt5\nwj1vevcXACQ3aIQlNAxHzdoqJxNCiMyXbQp5y5mN9N/TC3Bv6NCmfH96P9sdP4dsOO9ptBciMc+Y\ngvHTre5500/Xdc+bfvY5taMJIYRqsk0h1y38LANrDaVR8capGzoEBshG3J5Ee+0qpjkz8N6wDo3T\nSUq1GlhDx5D80ssyb1oIkeNlm0Iu4V+S0XXHqh1D3IcmOhrTgtn4rF7pnjddrjyWEaNJbv6GzJsW\nQog/ZZtCFp5HEx+Hz5IFmJYtRWO14CxW3D1vulVbmTcthBD/IL8VRfqzWPBZ8QGmRfPRxsfhzF8A\na9h4bB07y7xpIYT4D1LIIv3Y7fis/QjTvNnuedMBASSGTXDPmzbJ/tBCCPEgUsjiyTkceG/egGn2\n9P/Nmx46wj1v2j+X2umEECJLkEIWj8/lwvjZdkwzpqCPPI/i7Y21zwCs/Qej5M2rdjohhMhSpJDF\no1MUDN/sxjx1IvqTf7jnTXcJxjp4OK5ChdVOJ4QQWZIUsngkXvt/wDxlAl6HfnfPm27THsuwkbhK\nllI7mhBCZGlSyCJN9Id+d8+b3h8OgP21193zpitWUjeYEEJkE1LI4sGOHcM/ZCTGr78CILlRY/e8\n6Ro1VQ4mhBDZixSyuC9d5DlMM6bAju0YFYWUZ+phGT2WlLrPqh1NCCGyJSlk8Tfaq1GYZk/He9N6\nNE4n1KpFXMhoUho2lnnTQgiRgaSQBQCa27cxzZ+Fz5qP0CQn4yhfAcuIMeTq+g4pMYlqxxNCiGxP\nCjmH08TdxbR4AT4fLkVjteIsXuJ/86Z1OnlULIQQmUQKOadKTMT04VJ8Fi9AmxCPs0BBrGMnYXvn\nXTAY1E4nhBA5jhRyTmOz4bNmJab5s9HGxLjnTY+dRFLXbjJvWgghVCSFnFOkpOC9ab173vT1a7h8\n/bAMDyWpV18UP3+10wkhRI4nhZzduVwYP93qnjd98YJ73nTfgVj7D0LJI/OmhRDCU0ghZ1eKgmH3\nl5inTUJ/6gSKlxdJXbu5500XLKR2OiGEEP8ghZzdKApe+8IxT52AV8QhFK0WW9sO7nnTJUqqnU4I\nIcR/kELORvS//Yp56gQMB/YDYG/xpnvedPkKKicTQgjxMFLI2YDu+DHM0yZi/PZrAOwvNcEaGoaj\nepDKyYQQQqSVFHIWpjt/DtP0yXh/th2A5Hr1sYS+j6NuPZWTCSGEeFRSyFmQNuoKplnT8N68AY3L\nRUqNmlhGvU9Kg0YyWca2LLgAAAw0SURBVEsIIbIoKeQsRHPrFuZ5M/FeuwpNSgqOChWxjAwjuVlz\nKWIhhMjipJCzAM3dO5gWzcdnxQdokpJwliiJJWQU9pat3fOmhRBCZHlSyB5Mk3gPn2VL/q+9ew+K\n6r6jAH52F1Z2YcVHoL7SV8Ym1leqJg2xqIBVjPiIEFBCrAbRUTQRtaxoNDGJUdSi1SRqba1Wm9GJ\nk7E040xiaplJ6iNNJNb4ABOJOBhEhIhyd9lw+faPrZtHVVZZuD/wfP5i5K6cOaMeL7v7A7bXN8B8\ntQZ6127QXlwBd+pTQHCw0fGIiCiAOMgqcrlg2/Yn2Nf/DubLl9HQuTOuLXsFrinpgM1mdDoiImoG\nHGSVfP01Qt7YAXveKli+vIAGR3vUOhfDNWMWJMxhdDoiImpGHGQV6DravfUmQle9Asu5LyA2G7Q5\nWdBmPwvp2MnodERE1AI4yEYSgXXf2wjNfRlBp095z5tOnw5t7gI0/KCL0emIiKgFcZCNIILgggPe\n86Y/KYSYzXBNSoM234mGH/7I6HRERGQADnILCzp8yHve9KF/AQDcYx+H5lwMvefPDE5GRERG4iC3\nkKD/fAL7ipfQ7h/7AQB1vx4JbeFzqO/b3+BkRESkAg5yM7MUFyE0dzna/X0vAMDz6K9Qu+h51D/8\nS4OTERGRSjjIzcR87guErlmJdm/u8p43/YsBqM1Ziq+HxvCYSyIi+j8c5AAzXyyHPW8VQnZu9543\n3evnqHU+B8+o0RxiIiK6KQ5ygJiqLsO+YR1sW//gPW/6xz9BrXMx6sYn8rxpIiJqFAe5iUxXa7zn\nTW989Zvzpl/OhXvikzxvmoiI/ObXILvdbiQkJGDWrFmIiopCdnY2dF1HREQEVq9eDavVit69e2PA\ngAG+x2zbtg2Wtnxn6HLB9uc/es+brqpCwz334Fr2Crh+kw6EhBidjoiIWhm/Bnnjxo0IDw8HAKxf\nvx6pqakYNWoU8vLysGfPHqSmpiIsLAw7duxo1rBK8HgQ8te/wL52NSzlX6KhfThqc5ZAy5gJhIUZ\nnY6IiFopc2MXfP755/jss88wbNgwAMCRI0cQFxcHAIiJicGhQ4eaNaAydB3tdr+BTo8OgsM5D+aa\nK9CenY+qfx+DlvVbjjERETVJo3fIubm5WLJkCfbu9b6P1uVywWq1AgA6d+6MS5cuAQA8Hg/mz5+P\nsrIyjBw5ElOnTm30i3fsaEdQUPN+Wzsiook/JUkEeOstYOlS4ORJwGoFnnkGppwc2Lt0gT0wMZXW\n5A4JAHsMFPbYdOwwMALd4y0Hee/evXjwwQdx77333vDzIuL7ODs7G2PHjoXJZEJaWhoGDRqEvn37\n3vKLV1drdxDZfxERDly6dPXOHiyC4H++h9AVLyP4WCHEYoH7ycne86Z7/K+PO/29W5EmdUg+7DEw\n2GPTscPAuNMebzXitxzkgoICnD9/HgUFBSgvL4fVaoXdbofb7UZISAguXryIyMhIAMCkSZN8j3vk\nkUdQXFzc6CCrKvjwQdhfeRHWwwcBAO7HE6FlL4J+X0+DkxERUVt1y0Fet26d7+MNGzage/fuKCws\nxDvvvINx48bh3XffRXR0NM6ePYvXXnsNa9asga7rOHr0KOLj45s9fKAFHStE6IqXYD3wHgCgbuQo\n1Dqfg96ndf7HgoiIWo/bfh/ynDlz4HQ6sXv3bnTr1g3jx49HcHAwunTpgqSkJJjNZsTGxqJfv37N\nkbdZWIpOe8+bfvtvAABP9FDU5ixB/aCHDU5GRER3C5N8+4ngFtbcz2M09j1+8xcl3vOm9+z2njc9\ncJD3vOkhw5o1V2vC55sCgz0GBntsOnYYGC3+HHJbZS7/8pvzpuvrUd+rN2oXLYVnRDzPmyYiIkPc\nVYNsunwZ9g1rvedNu92o/+l90JyLUTduAmBu9C3ZREREzeauGGRTzRXYNr4K2+bXYb52FXr3HtAW\nLIQ7JRUIuisqICIixbXtNdI02Dasg/3VtTBXV6Phnghcy3kOrqem8rxpIiJSStscZI8HITu2Ab9f\ng7DycjSEd8C1xc/DlT6DR1wSEZGS2tYg19ej3Z7dCF2zEpbSc0BoKGqzFsA16xlIeAej0xEREd1U\nmxlky5litJ+SiqAzxRCrFdqMWbC/+Dw0k83oaERERI1qM4McdOI4LCVn4XpqCrR52Wjo3gP2CMdd\ncd40ERG1fm1mkOvGJ6JuzHjA0rw/PYqIiKg5tK0333KMiYiolWpbg0xERNRKcZCJiIgUwEEmIiJS\nAAeZiIhIARxkIiIiBXCQiYiIFMBBJiIiUgAHmYiISAEcZCIiIgVwkImIiBTAQSYiIlKASUTE6BBE\nRER3O94hExERKYCDTEREpAAOMhERkQI4yERERArgIBMRESmAg0xERKSAIKMDNNWqVavw8ccfo76+\nHjNmzMCIESMAAO+//z6mTZuGoqIiAMDp06exaNEiAEBcXBwyMzMNy6wif3tcu3Ytjhw5AhHB8OHD\nkZGRYWRspXy/wwMHDuDEiRPo0KEDACA9PR3Dhg1Dfn4+tm/fDrPZjOTkZDzxxBMGJ1eLvz3u27cP\nW7duhdlsRlRUFLKysgxOrhZ/e7xu3rx5sFqtWLlypUGJ1eNvhwHbF2nFDh06JNOmTRMRkaqqKhk6\ndKiIiLjdbklLS5PBgwf7rk1KSpJPP/1UdF2XrKws0TTNiMhK8rfHoqIiSUlJERERXdclPj5eKioq\nDMmsmht16HQ65cCBA9+5rra2VkaMGCE1NTXicrlk9OjRUl1dbURkJfnbo6ZpEhMTI1evXpWGhgZJ\nSkqSM2fOGBFZSf72eN0HH3wgiYmJ4nQ6WzKm0m6nw0DtS6u+Q37ooYfQr18/AED79u3hcrmg6zo2\nbdqE1NRUrF69GgBQWVkJTdPQu3dvAEBeXp5hmVXkb48OhwN1dXXweDzQdR1msxk2m83I6Mq4WYff\nd+zYMfTt2xcOhwMAMGDAABw9ehSxsbEtmldV/vZos9mQn5+PsLAwAECHDh3w1VdftWhWlfnbIwB4\nPB5s3LgRM2fOxP79+1syptL87TCQ+9Kqn0O2WCyw2+0AgD179mDIkCEoLS3F6dOnMWrUKN91ZWVl\nCA8Px8KFCzFx4kRs27bNoMRq8rfHrl27Ij4+HjExMYiJicHEiRN9/yDe7W7UocViwc6dOzF58mRk\nZWWhqqoKlZWV6NSpk+9xnTp1wqVLl4yKrRx/ewTg+7NXVFSEsrIy9O/f37DcqrmdHjdv3oxJkybx\n7/L3+NthQPelSff0iti/f78kJSVJTU2NZGRkyLlz50REJCYmRkRECgsLJTo6WqqqqkTTNBkzZowU\nFxcbGVlJjfVYWloqiYmJomma1NTUyGOPPSaVlZVGRlbOtzs8ePCgnDx5UkRENm/eLMuWLZP8/HxZ\nvny57/q8vDzZtWuXUXGV1ViP15WUlEhCQoLv8/RdjfVYUlIi06dPFxGRw4cP81vWN9BYh4Hcl1Z9\nhwx4X3S0adMmbNmyBZqm4ezZs1iwYAGSk5NRUVGBtLQ0dO7cGT179kTHjh1hs9kwcOBAnDlzxujo\nSvGnx+PHj6N///6w2WxwOBy4//77UVxcbHR0ZXy7Q4fDgaioKPTq1QsAEBsbi+LiYkRGRqKystL3\nmIqKCkRGRhoVWUn+9AgA5eXlyMzMxMqVK32fp2/402NBQQEuXLiA5ORkLFu2DAUFBdiyZYvBydXh\nT4cB3ZdA/k+ipdXU1EhCQsJN79Ku39mJiKSkpEh1dbXoui4pKSly6tSploqpPH97PH78uCQnJ4uu\n6+LxeGT06NFy/vz5loyqrBt1OHv2bCktLRURkZ07d8oLL7wgLpdLhg8fLleuXJFr1675XuBFXv72\nKCLy9NNPy4cffmhITtXdTo/X8Q75u26nw0DtS6t+Ude+fftQXV2NuXPn+n4tNzcX3bp1+79rc3Jy\nkJGRAZPJhOjoaDzwwAMtGVVp/vbYp08fDB48GKmpqQCApKQk9OjRo0WzqupGHU6YMAFz586FzWaD\n3W7HihUrEBISgvnz5yM9PR0mkwmZmZm+F3iR/z2WlJTgo48+wvr1633XTZkyBXFxcUbEVo6/PdLN\n3U6HgdoX/vhFIiIiBbT655CJiIjaAg4yERGRAjjIRERECuAgExERKYCDTEREpAAOMhERkQI4yERE\nRArgIBMRESngvy5pVG+fzySIAAAAAElFTkSuQmCC\n", - "text/plain": [ - "
\n",
+ "\n",
+ "\n",
+ " \n",
+ "
\n",
+ "
"
+ ],
+ "text/plain": [
+ " City name Population\n",
+ "0 San Francisco 852469\n",
+ "1 San Jose 1015785\n",
+ "2 Sacramento 485199"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 4
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "oa5wfZT7VHJl"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "But most of the time, you load an entire file into a `DataFrame`. The following example loads a file with California housing data. Run the following cell to load the data and create feature definitions:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "av6RYOraVG1V",
+ "outputId": "2168747e-41c4-4e0a-9ac5-bd2c212906e0",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 286
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "california_housing_dataframe = pd.read_csv(\"https://download.mlcc.google.com/mledu-datasets/california_housing_train.csv\", sep=\",\")\n",
+ "california_housing_dataframe.describe()"
+ ],
+ "execution_count": 5,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/html": [
+ "| \n", + " | City name | \n", + "Population | \n", + "
|---|---|---|
| 0 | \n", + "San Francisco | \n", + "852469 | \n", + "
| 1 | \n", + "San Jose | \n", + "1015785 | \n", + "
| 2 | \n", + "Sacramento | \n", + "485199 | \n", + "
\n",
+ "\n",
+ "\n",
+ " \n",
+ "
\n",
+ "
"
+ ],
+ "text/plain": [
+ " longitude latitude housing_median_age total_rooms \\\n",
+ "count 17000.000000 17000.000000 17000.000000 17000.000000 \n",
+ "mean -119.562108 35.625225 28.589353 2643.664412 \n",
+ "std 2.005166 2.137340 12.586937 2179.947071 \n",
+ "min -124.350000 32.540000 1.000000 2.000000 \n",
+ "25% -121.790000 33.930000 18.000000 1462.000000 \n",
+ "50% -118.490000 34.250000 29.000000 2127.000000 \n",
+ "75% -118.000000 37.720000 37.000000 3151.250000 \n",
+ "max -114.310000 41.950000 52.000000 37937.000000 \n",
+ "\n",
+ " total_bedrooms population households median_income \\\n",
+ "count 17000.000000 17000.000000 17000.000000 17000.000000 \n",
+ "mean 539.410824 1429.573941 501.221941 3.883578 \n",
+ "std 421.499452 1147.852959 384.520841 1.908157 \n",
+ "min 1.000000 3.000000 1.000000 0.499900 \n",
+ "25% 297.000000 790.000000 282.000000 2.566375 \n",
+ "50% 434.000000 1167.000000 409.000000 3.544600 \n",
+ "75% 648.250000 1721.000000 605.250000 4.767000 \n",
+ "max 6445.000000 35682.000000 6082.000000 15.000100 \n",
+ "\n",
+ " median_house_value \n",
+ "count 17000.000000 \n",
+ "mean 207300.912353 \n",
+ "std 115983.764387 \n",
+ "min 14999.000000 \n",
+ "25% 119400.000000 \n",
+ "50% 180400.000000 \n",
+ "75% 265000.000000 \n",
+ "max 500001.000000 "
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 5
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "WrkBjfz5kEQu"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "The example above used `DataFrame.describe` to show interesting statistics about a `DataFrame`. Another useful function is `DataFrame.head`, which displays the first few records of a `DataFrame`:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "s3ND3bgOkB5k",
+ "outputId": "f81980c5-2ce6-4494-b958-1647dc15d8e0",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 196
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "california_housing_dataframe.head()"
+ ],
+ "execution_count": 6,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/html": [
+ "| \n", + " | longitude | \n", + "latitude | \n", + "housing_median_age | \n", + "total_rooms | \n", + "total_bedrooms | \n", + "population | \n", + "households | \n", + "median_income | \n", + "median_house_value | \n", + "
|---|---|---|---|---|---|---|---|---|---|
| count | \n", + "17000.000000 | \n", + "17000.000000 | \n", + "17000.000000 | \n", + "17000.000000 | \n", + "17000.000000 | \n", + "17000.000000 | \n", + "17000.000000 | \n", + "17000.000000 | \n", + "17000.000000 | \n", + "
| mean | \n", + "-119.562108 | \n", + "35.625225 | \n", + "28.589353 | \n", + "2643.664412 | \n", + "539.410824 | \n", + "1429.573941 | \n", + "501.221941 | \n", + "3.883578 | \n", + "207300.912353 | \n", + "
| std | \n", + "2.005166 | \n", + "2.137340 | \n", + "12.586937 | \n", + "2179.947071 | \n", + "421.499452 | \n", + "1147.852959 | \n", + "384.520841 | \n", + "1.908157 | \n", + "115983.764387 | \n", + "
| min | \n", + "-124.350000 | \n", + "32.540000 | \n", + "1.000000 | \n", + "2.000000 | \n", + "1.000000 | \n", + "3.000000 | \n", + "1.000000 | \n", + "0.499900 | \n", + "14999.000000 | \n", + "
| 25% | \n", + "-121.790000 | \n", + "33.930000 | \n", + "18.000000 | \n", + "1462.000000 | \n", + "297.000000 | \n", + "790.000000 | \n", + "282.000000 | \n", + "2.566375 | \n", + "119400.000000 | \n", + "
| 50% | \n", + "-118.490000 | \n", + "34.250000 | \n", + "29.000000 | \n", + "2127.000000 | \n", + "434.000000 | \n", + "1167.000000 | \n", + "409.000000 | \n", + "3.544600 | \n", + "180400.000000 | \n", + "
| 75% | \n", + "-118.000000 | \n", + "37.720000 | \n", + "37.000000 | \n", + "3151.250000 | \n", + "648.250000 | \n", + "1721.000000 | \n", + "605.250000 | \n", + "4.767000 | \n", + "265000.000000 | \n", + "
| max | \n", + "-114.310000 | \n", + "41.950000 | \n", + "52.000000 | \n", + "37937.000000 | \n", + "6445.000000 | \n", + "35682.000000 | \n", + "6082.000000 | \n", + "15.000100 | \n", + "500001.000000 | \n", + "
\n",
+ "\n",
+ "\n",
+ " \n",
+ "
\n",
+ "
"
+ ],
+ "text/plain": [
+ " longitude latitude housing_median_age total_rooms total_bedrooms \\\n",
+ "0 -114.31 34.19 15.0 5612.0 1283.0 \n",
+ "1 -114.47 34.40 19.0 7650.0 1901.0 \n",
+ "2 -114.56 33.69 17.0 720.0 174.0 \n",
+ "3 -114.57 33.64 14.0 1501.0 337.0 \n",
+ "4 -114.57 33.57 20.0 1454.0 326.0 \n",
+ "\n",
+ " population households median_income median_house_value \n",
+ "0 1015.0 472.0 1.4936 66900.0 \n",
+ "1 1129.0 463.0 1.8200 80100.0 \n",
+ "2 333.0 117.0 1.6509 85700.0 \n",
+ "3 515.0 226.0 3.1917 73400.0 \n",
+ "4 624.0 262.0 1.9250 65500.0 "
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 6
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "w9-Es5Y6laGd"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Another powerful feature of *pandas* is graphing. For example, `DataFrame.hist` lets you quickly study the distribution of values in a column:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "nqndFVXVlbPN",
+ "outputId": "425c7814-fb16-441b-b529-912371ca3f57",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 395
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "california_housing_dataframe.hist('housing_median_age')"
+ ],
+ "execution_count": 7,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "array([[| \n", + " | longitude | \n", + "latitude | \n", + "housing_median_age | \n", + "total_rooms | \n", + "total_bedrooms | \n", + "population | \n", + "households | \n", + "median_income | \n", + "median_house_value | \n", + "
|---|---|---|---|---|---|---|---|---|---|
| 0 | \n", + "-114.31 | \n", + "34.19 | \n", + "15.0 | \n", + "5612.0 | \n", + "1283.0 | \n", + "1015.0 | \n", + "472.0 | \n", + "1.4936 | \n", + "66900.0 | \n", + "
| 1 | \n", + "-114.47 | \n", + "34.40 | \n", + "19.0 | \n", + "7650.0 | \n", + "1901.0 | \n", + "1129.0 | \n", + "463.0 | \n", + "1.8200 | \n", + "80100.0 | \n", + "
| 2 | \n", + "-114.56 | \n", + "33.69 | \n", + "17.0 | \n", + "720.0 | \n", + "174.0 | \n", + "333.0 | \n", + "117.0 | \n", + "1.6509 | \n", + "85700.0 | \n", + "
| 3 | \n", + "-114.57 | \n", + "33.64 | \n", + "14.0 | \n", + "1501.0 | \n", + "337.0 | \n", + "515.0 | \n", + "226.0 | \n", + "3.1917 | \n", + "73400.0 | \n", + "
| 4 | \n", + "-114.57 | \n", + "33.57 | \n", + "20.0 | \n", + "1454.0 | \n", + "326.0 | \n", + "624.0 | \n", + "262.0 | \n", + "1.9250 | \n", + "65500.0 | \n", + "
"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "XtYZ7114n3b-"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Accessing Data\n",
+ "\n",
+ "You can access `DataFrame` data using familiar Python dict/list operations:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "_TFm7-looBFF",
+ "outputId": "d7ab8f7b-e1e3-480c-a6f5-be3cf05dfc37",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 100
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "cities = pd.DataFrame({ 'City name': city_names, 'Population': population })\n",
+ "print(type(cities['City name']))\n",
+ "cities['City name']"
+ ],
+ "execution_count": 8,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "0 San Francisco\n",
+ "1 San Jose\n",
+ "2 Sacramento\n",
+ "Name: City name, dtype: object"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 8
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "V5L6xacLoxyv",
+ "outputId": "1319d6e2-f41e-4a35-a0ad-7ead83684577",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 50
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "print(type(cities['City name'][1]))\n",
+ "cities['City name'][1]"
+ ],
+ "execution_count": 9,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "'San Jose'"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 9
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "gcYX1tBPugZl",
+ "outputId": "927153f2-e74a-4256-ad8d-b6211ad065b9",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 124
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "print(type(cities[0:2]))\n",
+ "cities[0:2]"
+ ],
+ "execution_count": 10,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/html": [
+ " "
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "JndnmDMp66FL"
- },
- "cell_type": "markdown",
- "source": [
- "#### Copyright 2017 Google LLC."
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "hMqWDc_m6rUC",
- "cellView": "both",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Licensed under the Apache License, Version 2.0 (the \"License\");\n",
- "# you may not use this file except in compliance with the License.\n",
- "# You may obtain a copy of the License at\n",
- "#\n",
- "# https://www.apache.org/licenses/LICENSE-2.0\n",
- "#\n",
- "# Unless required by applicable law or agreed to in writing, software\n",
- "# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
- "# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
- "# See the License for the specific language governing permissions and\n",
- "# limitations under the License."
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "rHLcriKWLRe4"
- },
- "cell_type": "markdown",
- "source": [
- "# Intro to pandas"
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "QvJBqX8_Bctk"
- },
- "cell_type": "markdown",
- "source": [
- "**Learning Objectives:**\n",
- " * Gain an introduction to the `DataFrame` and `Series` data structures of the *pandas* library\n",
- " * Access and manipulate data within a `DataFrame` and `Series`\n",
- " * Import CSV data into a *pandas* `DataFrame`\n",
- " * Reindex a `DataFrame` to shuffle data"
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "TIFJ83ZTBctl"
- },
- "cell_type": "markdown",
- "source": [
- "[*pandas*](http://pandas.pydata.org/) is a column-oriented data analysis API. It's a great tool for handling and analyzing input data, and many ML frameworks support *pandas* data structures as inputs.\n",
- "Although a comprehensive introduction to the *pandas* API would span many pages, the core concepts are fairly straightforward, and we'll present them below. For a more complete reference, the [*pandas* docs site](http://pandas.pydata.org/pandas-docs/stable/index.html) contains extensive documentation and many tutorials."
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "s_JOISVgmn9v"
- },
- "cell_type": "markdown",
- "source": [
- "## Basic Concepts\n",
- "\n",
- "The following line imports the *pandas* API and prints the API version:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "aSRYu62xUi3g",
- "outputId": "4c052cad-dfa4-4fae-c502-c2e62f3fb85e",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 33
- }
- },
- "cell_type": "code",
- "source": [
- "from __future__ import print_function\n",
- "\n",
- "import pandas as pd\n",
- "pd.__version__"
- ],
- "execution_count": 2,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "u'0.22.0'"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 2
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "daQreKXIUslr"
- },
- "cell_type": "markdown",
- "source": [
- "The primary data structures in *pandas* are implemented as two classes:\n",
- "\n",
- " * **`DataFrame`**, which you can imagine as a relational data table, with rows and named columns.\n",
- " * **`Series`**, which is a single column. A `DataFrame` contains one or more `Series` and a name for each `Series`.\n",
- "\n",
- "The data frame is a commonly used abstraction for data manipulation. Similar implementations exist in [Spark](https://spark.apache.org/) and [R](https://www.r-project.org/about.html)."
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "fjnAk1xcU0yc"
- },
- "cell_type": "markdown",
- "source": [
- "One way to create a `Series` is to construct a `Series` object. For example:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "DFZ42Uq7UFDj",
- "outputId": "7f768471-8f34-4680-9fbc-0d4900311739",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 84
- }
- },
- "cell_type": "code",
- "source": [
- "pd.Series(['San Francisco', 'San Jose', 'Sacramento'])"
- ],
- "execution_count": 3,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "0 San Francisco\n",
- "1 San Jose\n",
- "2 Sacramento\n",
- "dtype: object"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 3
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "U5ouUp1cU6pC"
- },
- "cell_type": "markdown",
- "source": [
- "`DataFrame` objects can be created by passing a `dict` mapping `string` column names to their respective `Series`. If the `Series` don't match in length, missing values are filled with special [NA/NaN](http://pandas.pydata.org/pandas-docs/stable/missing_data.html) values. Example:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "avgr6GfiUh8t",
- "outputId": "24e4cefe-1dcd-402a-f3e9-f99414807ceb",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 137
- }
- },
- "cell_type": "code",
- "source": [
- "city_names = pd.Series(['San Francisco', 'San Jose', 'Sacramento'])\n",
- "population = pd.Series([852469, 1015785, 485199])\n",
- "\n",
- "pd.DataFrame({ 'City name': city_names, 'Population': population })"
- ],
- "execution_count": 4,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "
"
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "JndnmDMp66FL"
- },
- "cell_type": "markdown",
- "source": [
- "#### Copyright 2017 Google LLC."
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "hMqWDc_m6rUC",
- "cellView": "both",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Licensed under the Apache License, Version 2.0 (the \"License\");\n",
- "# you may not use this file except in compliance with the License.\n",
- "# You may obtain a copy of the License at\n",
- "#\n",
- "# https://www.apache.org/licenses/LICENSE-2.0\n",
- "#\n",
- "# Unless required by applicable law or agreed to in writing, software\n",
- "# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
- "# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
- "# See the License for the specific language governing permissions and\n",
- "# limitations under the License."
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "rHLcriKWLRe4"
- },
- "cell_type": "markdown",
- "source": [
- "# Intro to pandas"
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "QvJBqX8_Bctk"
- },
- "cell_type": "markdown",
- "source": [
- "**Learning Objectives:**\n",
- " * Gain an introduction to the `DataFrame` and `Series` data structures of the *pandas* library\n",
- " * Access and manipulate data within a `DataFrame` and `Series`\n",
- " * Import CSV data into a *pandas* `DataFrame`\n",
- " * Reindex a `DataFrame` to shuffle data"
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "TIFJ83ZTBctl"
- },
- "cell_type": "markdown",
- "source": [
- "[*pandas*](http://pandas.pydata.org/) is a column-oriented data analysis API. It's a great tool for handling and analyzing input data, and many ML frameworks support *pandas* data structures as inputs.\n",
- "Although a comprehensive introduction to the *pandas* API would span many pages, the core concepts are fairly straightforward, and we'll present them below. For a more complete reference, the [*pandas* docs site](http://pandas.pydata.org/pandas-docs/stable/index.html) contains extensive documentation and many tutorials."
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "s_JOISVgmn9v"
- },
- "cell_type": "markdown",
- "source": [
- "## Basic Concepts\n",
- "\n",
- "The following line imports the *pandas* API and prints the API version:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "aSRYu62xUi3g",
- "outputId": "4c052cad-dfa4-4fae-c502-c2e62f3fb85e",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 33
- }
- },
- "cell_type": "code",
- "source": [
- "from __future__ import print_function\n",
- "\n",
- "import pandas as pd\n",
- "pd.__version__"
- ],
- "execution_count": 2,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "u'0.22.0'"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 2
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "daQreKXIUslr"
- },
- "cell_type": "markdown",
- "source": [
- "The primary data structures in *pandas* are implemented as two classes:\n",
- "\n",
- " * **`DataFrame`**, which you can imagine as a relational data table, with rows and named columns.\n",
- " * **`Series`**, which is a single column. A `DataFrame` contains one or more `Series` and a name for each `Series`.\n",
- "\n",
- "The data frame is a commonly used abstraction for data manipulation. Similar implementations exist in [Spark](https://spark.apache.org/) and [R](https://www.r-project.org/about.html)."
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "fjnAk1xcU0yc"
- },
- "cell_type": "markdown",
- "source": [
- "One way to create a `Series` is to construct a `Series` object. For example:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "DFZ42Uq7UFDj",
- "outputId": "7f768471-8f34-4680-9fbc-0d4900311739",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 84
- }
- },
- "cell_type": "code",
- "source": [
- "pd.Series(['San Francisco', 'San Jose', 'Sacramento'])"
- ],
- "execution_count": 3,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "0 San Francisco\n",
- "1 San Jose\n",
- "2 Sacramento\n",
- "dtype: object"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 3
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "U5ouUp1cU6pC"
- },
- "cell_type": "markdown",
- "source": [
- "`DataFrame` objects can be created by passing a `dict` mapping `string` column names to their respective `Series`. If the `Series` don't match in length, missing values are filled with special [NA/NaN](http://pandas.pydata.org/pandas-docs/stable/missing_data.html) values. Example:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "avgr6GfiUh8t",
- "outputId": "24e4cefe-1dcd-402a-f3e9-f99414807ceb",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 137
- }
- },
- "cell_type": "code",
- "source": [
- "city_names = pd.Series(['San Francisco', 'San Jose', 'Sacramento'])\n",
- "population = pd.Series([852469, 1015785, 485199])\n",
- "\n",
- "pd.DataFrame({ 'City name': city_names, 'Population': population })"
- ],
- "execution_count": 4,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "]],\n",
- " dtype=object)"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 7
- },
- {
- "output_type": "display_data",
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeoAAAFZCAYAAABXM2zhAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3X1UlHX+//HXMDAH0UEEGTfLarf0\naEmaa5l4U0Iokp7IVRPWdU3q6Iqtlql499WTlajRmmZZmunRU7GNtofcAjJxyyRanT0uuu0p2VOr\neTejKCqgSPP7o9Os/FRguP1Az8dfcTEz1+d6H+3pdQ1zYfF6vV4BAAAjBTT3AgAAwPURagAADEao\nAQAwGKEGAMBghBoAAIMRagAADEaogVo6cuSI7rjjjkbdxz//+U+lpKQ06j4a0h133KEjR47o448/\n1ty5c5t7OUCrZOFz1EDtHDlyREOHDtW//vWv5l6KMe644w7l5ubqpptuau6lAK0WZ9SAn5xOp0aO\nHKn7779f27dv1w8//KA//elPio+PV3x8vNLS0lRaWipJiomJ0d69e33P/enry5cva/78+Ro2bJji\n4uI0bdo0nT9/XgUFBYqLi5MkrV69Ws8++6xSU1MVGxur0aNH6+TJk5KkgwcPaujQoRo6dKheeeUV\njRw5UgUFBdWue/Xq1Vq0aJEmT56sgQMHatasWcrLy9OoUaM0cOBA5eXlSZIuXbqk5557TsOGDVNM\nTIzWrl3re42//e1viouL0/Dhw7V+/Xrf9m3btmnixImSJI/Ho5SUFMXHxysmJkZvvfVWleN/9913\nNXr0aA0cOFDp6ek1zrusrEwzZszwrWfZsmW+71U3hx07dmjkyJGKjY3VpEmTdPr06Rr3BZiIUAN+\n+OGHH1RRUaEPPvhAc+fO1cqVK/XRRx/p008/1bZt2/TXv/5VJSUl2rhxY7Wvs3v3bh05ckTZ2dnK\nzc3V7bffrn/84x9XPS47O1vz5s3Tjh07FBERoa1bt0qSFi5cqIkTJyo3N1ft2rXTt99+W6v179q1\nSy+88II++OADZWdn+9Y9ZcoUrVu3TpK0bt06HTp0SB988IG2b9+unJwc5eXlqbKyUvPnz9eiRYv0\n0UcfKSAgQJWVlVft47XXXtNNN92k7Oxsbdq0SRkZGTp27Jjv+3//+9+VmZmprVu3asuWLTp+/Hi1\na37nnXd04cIFZWdn6/3339e2bdt8//i53hwOHz6s2bNnKyMjQ5988on69eunxYsX12pGgGkINeAH\nr9erxMREST9e9j1+/Lh27dqlxMREhYSEyGq1atSoUfr888+rfZ3w8HAVFRXp448/9p0xDho06KrH\n9e3bVzfeeKMsFot69OihY8eOqby8XAcPHtSIESMkSb/97W9V23ew7r77bkVERKhDhw6KjIzU4MGD\nJUndunXzna3n5eUpOTlZNptNISEhevjhh5Wbm6tvv/1Wly5d0sCBAyVJjzzyyDX3sWDBAi1cuFCS\n1KVLF0VGRurIkSO+748cOVJWq1WdOnVSRERElYhfy6RJk/Tqq6/KYrGoffv26tq1q44cOVLtHD79\n9FPde++96tatmyRp3Lhx2rlz5zX/YQGYLrC5FwC0JFarVW3atJEkBQQE6IcfftDp06fVvn1732Pa\nt2+vU6dOVfs6d911lxYsWKDNmzdrzpw5iomJ0aJFi656nN1ur7LvyspKnT17VhaLRaGhoZKkoKAg\nRURE1Gr9bdu2rfJ6ISEhVY5Fks6dO6elS5fqpZdekvTjpfC77rpLZ8+eVbt27aoc57UUFhb6zqID\nAgLkdrt9ry2pymv8dEzV+fbbb5Wenq7//Oc/CggI0PHjxzVq1Khq53Du3Dnt3btX8fHxVfZ75syZ\nWs8KMAWhBuqpY8eOOnPmjO/rM2fOqGPHjpKqBlCSzp496/vvn97TPnPmjObNm6c333xT0dHRNe6v\nXbt28nq9KisrU5s2bXT58uUGff/V4XBo0qRJGjJkSJXtRUVFOn/+vO/r6+1z1qxZ+v3vf6+kpCRZ\nLJZrXinwx7PPPqs777xTa9askdVq1bhx4yRVPweHw6Ho6GitWrWqXvsGTMClb6CeHnjgAWVlZams\nrEyXL1+W0+nU/fffL0mKjIzUv//9b0nShx9+qIsXL0qStm7dqjVr1kiSwsLC9Ktf/arW+2vbtq1u\nu+02ffTRR5KkzMxMWSyWBjue2NhYvffee6qsrJTX69Wrr76qTz/9VDfffLOsVqvvh7W2bdt2zf2e\nOnVKPXv2lMVi0fvvv6+ysjLfD9fVxalTp9SjRw9ZrVZ9/vnn+u6771RaWlrtHAYOHKi9e/fq8OHD\nkn782Ntzzz1X5zUAzYlQA/UUHx+vwYMHa9SoURoxYoR+8YtfaMKECZKkqVOnauPGjRoxYoSKiop0\n++23S/oxhj/9xPLw4cN16NAhPfbYY7Xe56JFi7R27Vo99NBDKi0tVadOnRos1snJyercubMeeugh\nxcfHq6ioSL/+9a8VFBSkJUuWaN68eRo+fLgsFovv0vmVpk+frtTUVI0cOVKlpaV69NFHtXDhQv33\nv/+t03r+8Ic/aNmyZRoxYoS+/PJLTZs2TatXr9a+ffuuOweHw6ElS5YoNTVVw4cP17PPPquEhIT6\njgZoFnyOGmihvF6vL8733XefNm7cqO7duzfzqpoec0Brxxk10AL98Y9/9H2cKj8/X16vV7feemvz\nLqoZMAf8HHBGDbRARUVFmjt3rs6ePaugoCDNmjVLN910k1JTU6/5+Ntuu833nrhpioqK6rzua83h\np58PAFoLQg0AgMG49A0AgMEINQAABjPyhidu9zm/Ht+hQ4iKi+v+Oc2fO+ZXd8yufphf3TG7+jFt\nfpGR9ut+r1WcUQcGWpt7CS0a86s7Zlc/zK/umF39tKT5tYpQAwDQWhFqAAAMRqgBADBYjT9MVlZW\nprS0NJ06dUoXL17U1KlT1b17d82ePVuVlZWKjIzUihUrZLPZlJWVpU2bNikgIEBjx47VmDFjVFFR\nobS0NB09elRWq1VLly5Vly5dmuLYAABo8Wo8o87Ly1PPnj21ZcsWrVy5Uunp6Vq1apWSk5P19ttv\n65ZbbpHT6VRpaanWrFmjjRs3avPmzdq0aZPOnDmj7du3KzQ0VO+8846mTJmijIyMpjguAABahRpD\nnZCQoCeeeEKSdOzYMXXq1EkFBQWKjY2VJA0ZMkT5+fnav3+/oqKiZLfbFRwcrD59+sjlcik/P19x\ncXGSpOjoaLlcrkY8HAAAWpdaf4563LhxOn78uNauXavHHntMNptNkhQRESG32y2Px6Pw8HDf48PD\nw6/aHhAQIIvFokuXLvmeDwAArq/WoX733Xf11VdfadasWbry9uDXu1W4v9uv1KFDiN+fcavuw+Ko\nGfOrO2ZXP8yv7phd/bSU+dUY6gMHDigiIkI33HCDevToocrKSrVt21bl5eUKDg7WiRMn5HA45HA4\n5PF4fM87efKkevfuLYfDIbfbre7du6uiokJer7fGs2l/7xYTGWn3+25m+B/mV3fMrn6YX90xu/ox\nbX71ujPZ3r17tWHDBkmSx+NRaWmpoqOjlZOTI0nKzc3VoEGD1KtXLxUWFqqkpEQXLlyQy+VS3759\nNWDAAGVnZ0v68QfT+vXr1xDHBADAz0KNZ9Tjxo3T/PnzlZycrPLycv3f//2fevbsqTlz5igzM1Od\nO3dWYmKigoKCNHPmTKWkpMhisSg1NVV2u10JCQnas2ePkpKSZLPZlJ6e3hTHBQBAq2Dk76P293KE\naZcwWhrmV3fMrn6YX90xu/oxbX7VXfo28rdnAcC1TErf2dxLqNGGtJjmXgJaGW4hCgCAwQg1AAAG\nI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCA\nwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMA\nYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QA\nABiMUAMAYDBCDQCAwQg1AAAGC6zNg5YvX659+/bp8uXLmjx5snbu3KmDBw8qLCxMkpSSkqIHHnhA\nWVlZ2rRpkwICAjR27FiNGTNGFRUVSktL09GjR2W1WrV06VJ16dKlUQ8KAIDWosZQf/HFF/rmm2+U\nmZmp4uJiPfLII7rvvvv09NNPa8iQIb7HlZaWas2aNXI6nQoKCtLo0aMVFxenvLw8hYaGKiMjQ7t3\n71ZGRoZWrlzZqAcFAEBrUeOl73vuuUcvv/yyJCk0NFRlZWWqrKy86nH79+9XVFSU7Ha7goOD1adP\nH7lcLuXn5ysuLk6SFB0dLZfL1cCHAABA61VjqK1Wq0JCQiRJTqdTgwcPltVq1ZYtWzRhwgQ99dRT\nOn36tDwej8LDw33PCw8Pl9vtrrI9ICBAFotFly5daqTDAQCgdanVe9SStGPHDjmdTm3YsEEHDhxQ\nWFiYevTooTfeeEOvvPKK7r777iqP93q913yd622/UocOIQoMtNZ2aZKkyEi7X49HVcyv7phd/bS2\n+TXl8bS22TW1ljK/WoX6s88+09q1a7V+/XrZ7Xb179/f972YmBgtXrxYw4YNk8fj8W0/efKkevfu\nLYfDIbfbre7du6uiokJer1c2m63a/RUXl/p1EJGRdrnd5/x6Dv6H+dUds6uf1ji/pjqe1ji7pmTa\n/Kr7R0ONl77PnTun5cuX6/XXX/f9lPeTTz6pw4cPS5IKCgrUtWtX9erVS4WFhSopKdGFCxfkcrnU\nt29fDRgwQNnZ2ZKkvLw89evXryGOCQCAn4Uaz6g//PBDFRcXa8aMGb5to0aN0owZM9SmTRuFhIRo\n6dKlCg4O1syZM5WSkiKLxaLU1FTZ7XYlJCRoz549SkpKks1mU3p6eqMeEAAArYnFW5s3jZuYv5cj\nTLuE0dIwv7pjdvXj7/wmpe9sxNU0jA1pMU2yH/7s1Y9p86vXpW8AANB8CDUAAAYj1AAAGIxQAwBg\nMEINAIDBCDUAAAYj1AAAGIxQAwBgMEINAIDBCDUAAAYj1AAAGIxQAwBgMEINAIDBCDUAAAYj1AAA\nGIxQAwBgMEINAIDBCDUAAAYj1AAAGIxQAwBgMEINAIDBCDUAAAYLbO4FAA1lUvrO5l5CtTakxTT3\nEgC0QJxRAwBgMEINAIDBCDUAAAYj1AAAGIxQAwBgMEINAIDBCDUAAAYj1AAAGIxQAwBgMEINAIDB\nCDUAAAYj1AAAGIxQAwBgMEINAIDBCDUAAAbj91EDTcT035ct8TuzARNxRg0AgMFqdUa9fPly7du3\nT5cvX9bkyZMVFRWl2bNnq7KyUpGRkVqxYoVsNpuysrK0adMmBQQEaOzYsRozZowqKiqUlpamo0eP\nymq1aunSperSpUtjHxcAAK1CjaH+4osv9M033ygzM1PFxcV65JFH1L9/fyUnJ2v48OF66aWX5HQ6\nlZiYqDVr1sjpdCooKEijR49WXFyc8vLyFBoaqoyMDO3evVsZGRlauXJlUxwbAAAtXo2Xvu+55x69\n/PLLkqTQ0FCVlZWpoKBAsbGxkqQhQ4YoPz9f+/fvV1RUlOx2u4KDg9WnTx+5XC7l5+crLi5OkhQd\nHS2Xy9WIhwMAQOtS4xm11WpVSEiIJMnpdGrw4MHavXu3bDabJCkiIkJut1sej0fh4eG+54WHh1+1\nPSAgQBaLRZcuXfI9/1o6dAhRYKDVrwOJjLT79XhUxfwgNc+fg9b2Z68pj6e1za6ptZT51fqnvnfs\n2CGn06kNGzZo6NChvu1er/eaj/d3+5WKi0truyxJPw7b7T7n13PwP8wPP2nqPwet8c9eUx1Pa5xd\nUzJtftX9o6FWP/X92Wefae3atVq3bp3sdrtCQkJUXl4uSTpx4oQcDoccDoc8Ho/vOSdPnvRtd7vd\nkqSKigp5vd5qz6YBAMD/1Bjqc+fOafny5Xr99dcVFhYm6cf3mnNyciRJubm5GjRokHr16qXCwkKV\nlJTowoULcrlc6tu3rwYMGKDs7GxJUl5envr169eIhwMAQOtS46XvDz/8UMXFxZoxY4ZvW3p6uhYs\nWKDMzEx17txZiYmJCgoK0syZM5WSkiKLxaLU1FTZ7XYlJCRoz549SkpKks1mU3p6eqMeEAAArUmN\noX700Uf16KOPXrX9rbfeumpbfHy84uPjq2z76bPTAADAf9xCFIBPS7jNKfBzwy1EAQAwGKEGAMBg\nhBoAAIMRagAADEaoAQAwGKEGAMBghBoAAIMRagAADEaoAQAwGHcmQ61wxyoAaB6cUQMAYDBCDQCA\nwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMA\nYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABgssLkXAADAlSal72zuJdRoQ1pM\nk+2LM2oAAAxGqAEAMBihBgDAYIQaAACDEWoAAAxGqAEAMBihBgDAYLX6HPXXX3+tqVOnauLEiRo/\nfrzS0tJ08OBBhYWFSZJSUlL0wAMPKCsrS5s2bVJAQIDGjh2rMWPGqKKiQmlpaTp69KisVquWLl2q\nLl26NOpBAUBz4TPAaGg1hrq0tFRLlixR//79q2x/+umnNWTIkCqPW7NmjZxOp4KCgjR69GjFxcUp\nLy9PoaGhysjI0O7du5WRkaGVK1c2/JEAANAK1Xjp22azad26dXI4HNU+bv/+/YqKipLdbldwcLD6\n9Okjl8ul/Px8xcXFSZKio6PlcrkaZuUAAPwM1BjqwMBABQcHX7V9y5YtmjBhgp566imdPn1aHo9H\n4eHhvu+Hh4fL7XZX2R4QECCLxaJLly414CEAANB61ele3w8//LDCwsLUo0cPvfHGG3rllVd09913\nV3mM1+u95nOvt/1KHTqEKDDQ6teaIiPtfj0eVTE/4OeDv+/115QzrFOor3y/OiYmRosXL9awYcPk\n8Xh820+ePKnevXvL4XDI7Xare/fuqqiokNfrlc1mq/b1i4tL/VpPZKRdbvc5/w4CPswP+Hnh73v9\nNfQMqwt/nT6e9eSTT+rw4cOSpIKCAnXt2lW9evVSYWGhSkpKdOHCBblcLvXt21cDBgxQdna2JCkv\nL0/9+vWryy4BAPhZqvGM+sCBA1q2bJm+//57BQYGKicnR+PHj9eMGTPUpk0bhYSEaOnSpQoODtbM\nmTOVkpIii8Wi1NRU2e12JSQkaM+ePUpKSpLNZlN6enpTHBcAAK1CjaHu2bOnNm/efNX2YcOGXbUt\nPj5e8fHxVbb99NlpAADgP+5MBgCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMA\nYDBCDQCAwQg1AAAGI9QAABiMUAMAYLA6/T5qAEDLNSl9Z3MvAX7gjBoAAIMRagAADEaoAQAwGKEG\nAMBghBoAAIMRagAADEaoAQAwGKEGAMBghBoAAIMRagAADEaoAQAwGKEGAMBghBoAAIMRagAADEao\nAQAwGKEGAMBghBoAAIMRagAADEaoAQAwGKEGAMBghBoAAIMRagAADEaoAQAwGKEGAMBghBoAAIMR\nagAADFarUH/99dd68MEHtWXLFknSsWPH9Lvf/U7JycmaPn26Ll26JEnKysrSb37zG40ZM0bvvfee\nJKmiokIzZ85UUlKSxo8fr8OHDzfSoQAA0PrUGOrS0lItWbJE/fv3921btWqVkpOT9fbbb+uWW26R\n0+lUaWmp1qxZo40bN2rz5s3atGmTzpw5o+3btys0NFTvvPOOpkyZooyMjEY9IAAAWpMaQ22z2bRu\n3To5HA7ftoKCAsXGxkqShgwZovz8fO3fv19RUVGy2+0KDg5Wnz595HK5lJ+fr7i4OElSdHS0XC5X\nIx0KAACtT42hDgwMVHBwcJVtZWVlstlskqSIiAi53W55PB6Fh4f7HhMeHn7V9oCAAFksFt+lcgAA\nUL3A+r6A1+ttkO1X6tAhRIGBVr/WERlp9+vxqIr5AUDtNeX/M+sU6pCQEJWXlys4OFgnTpyQw+GQ\nw+GQx+PxPebkyZPq3bu3HA6H3G63unfvroqKCnm9Xt/Z+PUUF5f6tZ7ISLvc7nN1ORSI+QGAvxr6\n/5nVhb9OH8+Kjo5WTk6OJCk3N1eDBg1Sr169VFhYqJKSEl24cEEul0t9+/bVgAEDlJ2dLUnKy8tT\nv3796rJLAAB+lmo8oz5w4ICWLVum77//XoGBgcrJydGLL76otLQ0ZWZmqnPnzkpMTFRQUJBmzpyp\nlJQUWSwWpaamym63KyEhQXv27FFSUpJsNpvS09Ob4rgAAGgVLN7avGncxPy9pMCl2/qpzfwmpe9s\notUAgPk2pMU06Os1+KVvAADQNOr9U99oGJyxAgCuhTNqAAAMRqgBADAYoQYAwGCEGgAAgxFqAAAM\nRqgBADAYoQYAwGCEGgAAgxFqAAAMRqgBADAYoQYAwGCEGgAAgxFqAAAMRqgBADAYoQYAwGCEGgAA\ngxFqAAAMRqgBADAYoQYAwGCEGgAAgxFqAAAMRqgBADAYoQYAwGCEGgAAgxFqAAAMRqgBADAYoQYA\nwGCEGgAAgxFqAAAMRqgBADAYoQYAwGCEGgAAgxFqAAAMFtjcC2gKk9J3NvcSAACoE86oAQAwGKEG\nAMBghBoAAIMRagAADFanHyYrKCjQ9OnT1bVrV0lSt27d9Pjjj2v27NmqrKxUZGSkVqxYIZvNpqys\nLG3atEkBAQEaO3asxowZ06AHAABAa1bnn/q+9957tWrVKt/Xc+fOVXJysoYPH66XXnpJTqdTiYmJ\nWrNmjZxOp4KCgjR69GjFxcUpLCysQRYPAEBr12CXvgsKChQbGytJGjJkiPLz87V//35FRUXJbrcr\nODhYffr0kcvlaqhdAgDQ6tX5jPrQoUOaMmWKzp49q2nTpqmsrEw2m02SFBERIbfbLY/Ho/DwcN9z\nwsPD5Xa7a3ztDh1CFBho9Ws9kZF2/w4AAIA6asrm1CnUt956q6ZNm6bhw4fr8OHDmjBhgiorK33f\n93q913ze9bb//4qLS/1aT2SkXW73Ob+eAwBAXTV0c6oLf50ufXfq1EkJCQmyWCy6+eab1bFjR509\ne1bl5eWSpBMnTsjhcMjhcMjj8fied/LkSTkcjrrsEgCAn6U6hTorK0tvvvmmJMntduvUqVMaNWqU\ncnJyJEm5ubkaNGiQevXqpcLCQpWUlOjChQtyuVzq27dvw60eAIBWrk6XvmNiYvTMM8/ok08+UUVF\nhRYvXqwePXpozpw5yszMVOfOnZWYmKigoCDNnDlTKSkpslgsSk1Nld3Oe8kAANSWxVvbN46bkL/X\n/mt6j5pfygEAaEgb0mIa9PUa/D1qAADQNAg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiM\nUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAG\nI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCA\nwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABiMUAMAYDBCDQCAwQg1AAAGI9QAABgssCl2\n8sILL2j//v2yWCyaN2+e7rrrrqbYLQAALV6jh/rLL7/Ud999p8zMTBUVFWnevHnKzMxs7N0CANAq\nNPql7/z8fD344IOSpNtuu01nz57V+fPnG3u3AAC0Co0eao/How4dOvi+Dg8Pl9vtbuzdAgDQKjTJ\ne9RX8nq9NT4mMtLu9+tW95wPMh72+/UAADBBo59ROxwOeTwe39cnT55UZGRkY+8WAIBWodFDPWDA\nAOXk5EiSDh48KIfDoXbt2jX2bgEAaBUa/dJ3nz59dOedd2rcuHGyWCxatGhRY+8SAIBWw+KtzZvG\nAACgWXBnMgAADEaoAQAwWJN/PKuhcXtS/3399deaOnWqJk6cqPHjx+vYsWOaPXu2KisrFRkZqRUr\nVshmszX3Mo20fPly7du3T5cvX9bkyZMVFRXF7GqhrKxMaWlpOnXqlC5evKipU6eqe/fuzM5P5eXl\nGjFihKZOnar+/fszv1oqKCjQ9OnT1bVrV0lSt27d9Pjjj7eY+bXoM+orb0/6/PPP6/nnn2/uJRmv\ntLRUS5YsUf/+/X3bVq1apeTkZL399tu65ZZb5HQ6m3GF5vriiy/0zTffKDMzU+vXr9cLL7zA7Gop\nLy9PPXv21JYtW7Ry5Uqlp6czuzp47bXX1L59e0n8vfXXvffeq82bN2vz5s1auHBhi5pfiw41tyf1\nn81m07p16+RwOHzbCgoKFBsbK0kaMmSI8vPzm2t5Rrvnnnv08ssvS5JCQ0NVVlbG7GopISFBTzzx\nhCTp2LFj6tSpE7PzU1FRkQ4dOqQHHnhAEn9v66slza9Fh5rbk/ovMDBQwcHBVbaVlZX5LvlEREQw\nw+uwWq0KCQmRJDmdTg0ePJjZ+WncuHF65plnNG/ePGbnp2XLliktLc33NfPzz6FDhzRlyhQlJSXp\n888/b1Hza/HvUV+JT5rVHzOs2Y4dO+R0OrVhwwYNHTrUt53Z1ezdd9/VV199pVmzZlWZF7Or3l/+\n8hf17t1bXbp0ueb3mV/1br31Vk2bNk3Dhw/X4cOHNWHCBFVWVvq+b/r8WnSouT1pwwgJCVF5ebmC\ng4N14sSJKpfFUdVnn32mtWvXav369bLb7cyulg4cOKCIiAjdcMMN6tGjhyorK9W2bVtmV0u7du3S\n4cOHtWvXLh0/flw2m40/e37o1KmTEhISJEk333yzOnbsqMLCwhYzvxZ96ZvbkzaM6Oho3xxzc3M1\naNCgZl6Rmc6dO6fly5fr9ddfV1hYmCRmV1t79+7Vhg0bJP34llVpaSmz88PKlSu1detW/fnPf9aY\nMWM0depU5ueHrKwsvfnmm5Ikt9utU6dOadSoUS1mfi3+zmQvvvii9u7d67s9affu3Zt7SUY7cOCA\nli1bpu+//16BgYHq1KmTXnytKYqYAAAArElEQVTxRaWlpenixYvq3Lmzli5dqqCgoOZeqnEyMzO1\nevVq/fKXv/RtS09P14IFC5hdDcrLyzV//nwdO3ZM5eXlmjZtmnr27Kk5c+YwOz+tXr1aN954owYO\nHMj8aun8+fN65plnVFJSooqKCk2bNk09evRoMfNr8aEGAKA1a9GXvgEAaO0INQAABiPUAAAYjFAD\nAGAwQg0AgMEINQAABiPUAAAYjFADAGCw/wdkB5RjykY3PgAAAABJRU5ErkJggg==\n",
- "text/plain": [
- "
\n",
+ "\n",
+ "\n",
+ " \n",
+ "
\n",
+ "
"
+ ],
+ "text/plain": [
+ " City name Population\n",
+ "0 San Francisco 852469\n",
+ "1 San Jose 1015785"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 10
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "65g1ZdGVjXsQ"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "In addition, *pandas* provides an extremely rich API for advanced [indexing and selection](http://pandas.pydata.org/pandas-docs/stable/indexing.html) that is too extensive to be covered here."
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "RM1iaD-ka3Y1"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Manipulating Data\n",
+ "\n",
+ "You may apply Python's basic arithmetic operations to `Series`. For example:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "XWmyCFJ5bOv-",
+ "outputId": "91280582-c473-48cd-c7f5-36a8a73df7e9",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 84
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "population / 1000."
+ ],
+ "execution_count": 11,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "0 852.469\n",
+ "1 1015.785\n",
+ "2 485.199\n",
+ "dtype: float64"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 11
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "TQzIVnbnmWGM"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "[NumPy](http://www.numpy.org/) is a popular toolkit for scientific computing. *pandas* `Series` can be used as arguments to most NumPy functions:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "ko6pLK6JmkYP",
+ "outputId": "92b5b7fd-95be-4fc5-8033-5b8da8b2a95b",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 84
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "import numpy as np\n",
+ "\n",
+ "np.log(population)"
+ ],
+ "execution_count": 12,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "0 13.655892\n",
+ "1 13.831172\n",
+ "2 13.092314\n",
+ "dtype: float64"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 12
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "xmxFuQmurr6d"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "For more complex single-column transformations, you can use `Series.apply`. Like the Python [map function](https://docs.python.org/2/library/functions.html#map), \n",
+ "`Series.apply` accepts as an argument a [lambda function](https://docs.python.org/2/tutorial/controlflow.html#lambda-expressions), which is applied to each value.\n",
+ "\n",
+ "The example below creates a new `Series` that indicates whether `population` is over one million:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "Fc1DvPAbstjI",
+ "outputId": "e447f694-479c-4964-fa8e-4e5bfebad9cc",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 84
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "population.apply(lambda val: val > 1000000)"
+ ],
+ "execution_count": 13,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "0 False\n",
+ "1 True\n",
+ "2 False\n",
+ "dtype: bool"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 13
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "ZeYYLoV9b9fB"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "\n",
+ "Modifying `DataFrames` is also straightforward. For example, the following code adds two `Series` to an existing `DataFrame`:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "0gCEX99Hb8LR",
+ "outputId": "7d96cf32-a00a-4c43-81d1-88953ab65041",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 137
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "cities['Area square miles'] = pd.Series([46.87, 176.53, 97.92])\n",
+ "cities['Population density'] = cities['Population'] / cities['Area square miles']\n",
+ "cities"
+ ],
+ "execution_count": 14,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/html": [
+ "| \n", + " | City name | \n", + "Population | \n", + "
|---|---|---|
| 0 | \n", + "San Francisco | \n", + "852469 | \n", + "
| 1 | \n", + "San Jose | \n", + "1015785 | \n", + "
\n",
+ "\n",
+ "\n",
+ " \n",
+ "
\n",
+ "
"
+ ],
+ "text/plain": [
+ " City name Population Area square miles Population density\n",
+ "0 San Francisco 852469 46.87 18187.945381\n",
+ "1 San Jose 1015785 176.53 5754.177760\n",
+ "2 Sacramento 485199 97.92 4955.055147"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 14
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "6qh63m-ayb-c"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Exercise #1\n",
+ "\n",
+ "Modify the `cities` table by adding a new boolean column that is True if and only if *both* of the following are True:\n",
+ "\n",
+ " * The city is named after a saint.\n",
+ " * The city has an area greater than 50 square miles.\n",
+ "\n",
+ "**Note:** Boolean `Series` are combined using the bitwise, rather than the traditional boolean, operators. For example, when performing *logical and*, use `&` instead of `and`.\n",
+ "\n",
+ "**Hint:** \"San\" in Spanish means \"saint.\""
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "zCOn8ftSyddH",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 137
+ },
+ "outputId": "508be6c9-95f2-432c-be0a-e2f2d24e8886"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Your code here\n",
+ "cities['Wide and has saint name'] = (cities['Area square miles'] > 50) & cities['City name'].apply(lambda name: name.startswith('San'))\n",
+ "cities"
+ ],
+ "execution_count": 15,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/html": [
+ "| \n", + " | City name | \n", + "Population | \n", + "Area square miles | \n", + "Population density | \n", + "
|---|---|---|---|---|
| 0 | \n", + "San Francisco | \n", + "852469 | \n", + "46.87 | \n", + "18187.945381 | \n", + "
| 1 | \n", + "San Jose | \n", + "1015785 | \n", + "176.53 | \n", + "5754.177760 | \n", + "
| 2 | \n", + "Sacramento | \n", + "485199 | \n", + "97.92 | \n", + "4955.055147 | \n", + "
\n",
+ "\n",
+ "\n",
+ " \n",
+ "
\n",
+ "
"
+ ],
+ "text/plain": [
+ " City name Population Area square miles Population density \\\n",
+ "0 San Francisco 852469 46.87 18187.945381 \n",
+ "1 San Jose 1015785 176.53 5754.177760 \n",
+ "2 Sacramento 485199 97.92 4955.055147 \n",
+ "\n",
+ " Wide and has saint name \n",
+ "0 False \n",
+ "1 True \n",
+ "2 False "
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 15
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "YHIWvc9Ms-Ll"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "### Solution\n",
+ "\n",
+ "Click below for a solution."
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "T5OlrqtdtCIb",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "cities['Is wide and has saint name'] = (cities['Area square miles'] > 50) & cities['City name'].apply(lambda name: name.startswith('San'))\n",
+ "cities"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "f-xAOJeMiXFB"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Indexes\n",
+ "Both `Series` and `DataFrame` objects also define an `index` property that assigns an identifier value to each `Series` item or `DataFrame` row. \n",
+ "\n",
+ "By default, at construction, *pandas* assigns index values that reflect the ordering of the source data. Once created, the index values are stable; that is, they do not change when data is reordered."
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "2684gsWNinq9",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 33
+ },
+ "outputId": "11071fbe-39ca-482f-b66f-e3a7e7e28996"
+ },
+ "cell_type": "code",
+ "source": [
+ "city_names.index"
+ ],
+ "execution_count": 16,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "RangeIndex(start=0, stop=3, step=1)"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 16
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "F_qPe2TBjfWd",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 33
+ },
+ "outputId": "42bb63a5-5a3c-494a-8d99-b324a91dea7c"
+ },
+ "cell_type": "code",
+ "source": [
+ "cities.index"
+ ],
+ "execution_count": 17,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "RangeIndex(start=0, stop=3, step=1)"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 17
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "hp2oWY9Slo_h"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Call `DataFrame.reindex` to manually reorder the rows. For example, the following has the same effect as sorting by city name:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "sN0zUzSAj-U1",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 137
+ },
+ "outputId": "6f05c626-0057-43e2-d444-e6c50622ac44"
+ },
+ "cell_type": "code",
+ "source": [
+ "cities.reindex([2, 0, 1])"
+ ],
+ "execution_count": 18,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/html": [
+ "| \n", + " | City name | \n", + "Population | \n", + "Area square miles | \n", + "Population density | \n", + "Wide and has saint name | \n", + "
|---|---|---|---|---|---|
| 0 | \n", + "San Francisco | \n", + "852469 | \n", + "46.87 | \n", + "18187.945381 | \n", + "False | \n", + "
| 1 | \n", + "San Jose | \n", + "1015785 | \n", + "176.53 | \n", + "5754.177760 | \n", + "True | \n", + "
| 2 | \n", + "Sacramento | \n", + "485199 | \n", + "97.92 | \n", + "4955.055147 | \n", + "False | \n", + "
\n",
+ "\n",
+ "\n",
+ " \n",
+ "
\n",
+ "
"
+ ],
+ "text/plain": [
+ " City name Population Area square miles Population density \\\n",
+ "2 Sacramento 485199 97.92 4955.055147 \n",
+ "0 San Francisco 852469 46.87 18187.945381 \n",
+ "1 San Jose 1015785 176.53 5754.177760 \n",
+ "\n",
+ " Wide and has saint name \n",
+ "2 False \n",
+ "0 False \n",
+ "1 True "
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 18
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "-GQFz8NZuS06"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Reindexing is a great way to shuffle (randomize) a `DataFrame`. In the example below, we take the index, which is array-like, and pass it to NumPy's `random.permutation` function, which shuffles its values in place. Calling `reindex` with this shuffled array causes the `DataFrame` rows to be shuffled in the same way.\n",
+ "Try running the following cell multiple times!"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "mF8GC0k8uYhz",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 137
+ },
+ "outputId": "5496dd16-e56e-4b2d-a68c-039690cb4a57"
+ },
+ "cell_type": "code",
+ "source": [
+ "cities.reindex(np.random.permutation(cities.index))"
+ ],
+ "execution_count": 24,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/html": [
+ "| \n", + " | City name | \n", + "Population | \n", + "Area square miles | \n", + "Population density | \n", + "Wide and has saint name | \n", + "
|---|---|---|---|---|---|
| 2 | \n", + "Sacramento | \n", + "485199 | \n", + "97.92 | \n", + "4955.055147 | \n", + "False | \n", + "
| 0 | \n", + "San Francisco | \n", + "852469 | \n", + "46.87 | \n", + "18187.945381 | \n", + "False | \n", + "
| 1 | \n", + "San Jose | \n", + "1015785 | \n", + "176.53 | \n", + "5754.177760 | \n", + "True | \n", + "
\n",
+ "\n",
+ "\n",
+ " \n",
+ "
\n",
+ "
"
+ ],
+ "text/plain": [
+ " City name Population Area square miles Population density \\\n",
+ "2 Sacramento 485199 97.92 4955.055147 \n",
+ "0 San Francisco 852469 46.87 18187.945381 \n",
+ "1 San Jose 1015785 176.53 5754.177760 \n",
+ "\n",
+ " Wide and has saint name \n",
+ "2 False \n",
+ "0 False \n",
+ "1 True "
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 24
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "fSso35fQmGKb"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "For more information, see the [Index documentation](http://pandas.pydata.org/pandas-docs/stable/indexing.html#index-objects)."
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "8UngIdVhz8C0"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Exercise #2\n",
+ "\n",
+ "The `reindex` method allows index values that are not in the original `DataFrame`'s index values. Try it and see what happens if you use such values! Why do you think this is allowed?"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "PN55GrDX0jzO",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 166
+ },
+ "outputId": "37aab3dd-e4b4-4afe-8bdb-52da45962509"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Your code here\n",
+ "cities.reindex([2, 0, 1, 4])"
+ ],
+ "execution_count": 25,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/html": [
+ "| \n", + " | City name | \n", + "Population | \n", + "Area square miles | \n", + "Population density | \n", + "Wide and has saint name | \n", + "
|---|---|---|---|---|---|
| 2 | \n", + "Sacramento | \n", + "485199 | \n", + "97.92 | \n", + "4955.055147 | \n", + "False | \n", + "
| 0 | \n", + "San Francisco | \n", + "852469 | \n", + "46.87 | \n", + "18187.945381 | \n", + "False | \n", + "
| 1 | \n", + "San Jose | \n", + "1015785 | \n", + "176.53 | \n", + "5754.177760 | \n", + "True | \n", + "
\n",
+ "\n",
+ "\n",
+ " \n",
+ "
\n",
+ "
"
+ ],
+ "text/plain": [
+ " City name Population Area square miles Population density \\\n",
+ "2 Sacramento 485199.0 97.92 4955.055147 \n",
+ "0 San Francisco 852469.0 46.87 18187.945381 \n",
+ "1 San Jose 1015785.0 176.53 5754.177760 \n",
+ "4 NaN NaN NaN NaN \n",
+ "\n",
+ " Wide and has saint name \n",
+ "2 False \n",
+ "0 False \n",
+ "1 True \n",
+ "4 NaN "
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 25
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "TJffr5_Jwqvd"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "### Solution\n",
+ "\n",
+ "Click below for the solution."
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "8oSvi2QWwuDH"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "If your `reindex` input array includes values not in the original `DataFrame` index values, `reindex` will add new rows for these \"missing\" indices and populate all corresponding columns with `NaN` values:"
+ ]
+ },
+ {
+ "metadata": {
+ "colab_type": "code",
+ "id": "yBdkucKCwy4x",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "cities.reindex([0, 4, 5, 2])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "colab_type": "text",
+ "id": "2l82PhPbwz7g"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "This behavior is desirable because indexes are often strings pulled from the actual data (see the [*pandas* reindex\n",
+ "documentation](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.reindex.html) for an example\n",
+ "in which the index values are browser names).\n",
+ "\n",
+ "In this case, allowing \"missing\" indices makes it easy to reindex using an external list, as you don't have to worry about\n",
+ "sanitizing the input."
+ ]
+ }
+ ]
+}
\ No newline at end of file
From f36ff1941bce5a23e92fd8d545a62935bc7d5cda Mon Sep 17 00:00:00 2001
From: Anubhab-Bob <43186348+Anubhab-Bob@users.noreply.github.com>
Date: Mon, 21 Jan 2019 16:39:34 +0530
Subject: [PATCH 12/12] Delete Intro_to_pandas.ipynb
---
Intro_to_pandas.ipynb | 1703 -----------------------------------------
1 file changed, 1703 deletions(-)
delete mode 100644 Intro_to_pandas.ipynb
diff --git a/Intro_to_pandas.ipynb b/Intro_to_pandas.ipynb
deleted file mode 100644
index e968a90..0000000
--- a/Intro_to_pandas.ipynb
+++ /dev/null
@@ -1,1703 +0,0 @@
-{
- "nbformat": 4,
- "nbformat_minor": 0,
- "metadata": {
- "colab": {
- "name": "Copy of intro_to_pandas.ipynb",
- "version": "0.3.2",
- "provenance": [],
- "collapsed_sections": [
- "JndnmDMp66FL",
- "YHIWvc9Ms-Ll",
- "TJffr5_Jwqvd"
- ],
- "include_colab_link": true
- },
- "kernelspec": {
- "name": "python2",
- "display_name": "Python 2"
- }
- },
- "cells": [
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "view-in-github",
- "colab_type": "text"
- },
- "source": [
- "| \n", + " | City name | \n", + "Population | \n", + "Area square miles | \n", + "Population density | \n", + "Wide and has saint name | \n", + "
|---|---|---|---|---|---|
| 2 | \n", + "Sacramento | \n", + "485199.0 | \n", + "97.92 | \n", + "4955.055147 | \n", + "False | \n", + "
| 0 | \n", + "San Francisco | \n", + "852469.0 | \n", + "46.87 | \n", + "18187.945381 | \n", + "False | \n", + "
| 1 | \n", + "San Jose | \n", + "1015785.0 | \n", + "176.53 | \n", + "5754.177760 | \n", + "True | \n", + "
| 4 | \n", + "NaN | \n", + "NaN | \n", + "NaN | \n", + "NaN | \n", + "NaN | \n", + "
\n",
- "\n",
- "\n",
- " \n",
- "
\n",
- "
"
- ],
- "text/plain": [
- " City name Population\n",
- "0 San Francisco 852469\n",
- "1 San Jose 1015785\n",
- "2 Sacramento 485199"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 4
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "oa5wfZT7VHJl"
- },
- "cell_type": "markdown",
- "source": [
- "But most of the time, you load an entire file into a `DataFrame`. The following example loads a file with California housing data. Run the following cell to load the data and create feature definitions:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "av6RYOraVG1V",
- "outputId": "2168747e-41c4-4e0a-9ac5-bd2c212906e0",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 286
- }
- },
- "cell_type": "code",
- "source": [
- "california_housing_dataframe = pd.read_csv(\"https://download.mlcc.google.com/mledu-datasets/california_housing_train.csv\", sep=\",\")\n",
- "california_housing_dataframe.describe()"
- ],
- "execution_count": 5,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "| \n", - " | City name | \n", - "Population | \n", - "
|---|---|---|
| 0 | \n", - "San Francisco | \n", - "852469 | \n", - "
| 1 | \n", - "San Jose | \n", - "1015785 | \n", - "
| 2 | \n", - "Sacramento | \n", - "485199 | \n", - "
\n",
- "\n",
- "\n",
- " \n",
- "
\n",
- "
"
- ],
- "text/plain": [
- " longitude latitude housing_median_age total_rooms \\\n",
- "count 17000.000000 17000.000000 17000.000000 17000.000000 \n",
- "mean -119.562108 35.625225 28.589353 2643.664412 \n",
- "std 2.005166 2.137340 12.586937 2179.947071 \n",
- "min -124.350000 32.540000 1.000000 2.000000 \n",
- "25% -121.790000 33.930000 18.000000 1462.000000 \n",
- "50% -118.490000 34.250000 29.000000 2127.000000 \n",
- "75% -118.000000 37.720000 37.000000 3151.250000 \n",
- "max -114.310000 41.950000 52.000000 37937.000000 \n",
- "\n",
- " total_bedrooms population households median_income \\\n",
- "count 17000.000000 17000.000000 17000.000000 17000.000000 \n",
- "mean 539.410824 1429.573941 501.221941 3.883578 \n",
- "std 421.499452 1147.852959 384.520841 1.908157 \n",
- "min 1.000000 3.000000 1.000000 0.499900 \n",
- "25% 297.000000 790.000000 282.000000 2.566375 \n",
- "50% 434.000000 1167.000000 409.000000 3.544600 \n",
- "75% 648.250000 1721.000000 605.250000 4.767000 \n",
- "max 6445.000000 35682.000000 6082.000000 15.000100 \n",
- "\n",
- " median_house_value \n",
- "count 17000.000000 \n",
- "mean 207300.912353 \n",
- "std 115983.764387 \n",
- "min 14999.000000 \n",
- "25% 119400.000000 \n",
- "50% 180400.000000 \n",
- "75% 265000.000000 \n",
- "max 500001.000000 "
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 5
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "WrkBjfz5kEQu"
- },
- "cell_type": "markdown",
- "source": [
- "The example above used `DataFrame.describe` to show interesting statistics about a `DataFrame`. Another useful function is `DataFrame.head`, which displays the first few records of a `DataFrame`:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "s3ND3bgOkB5k",
- "outputId": "f81980c5-2ce6-4494-b958-1647dc15d8e0",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 196
- }
- },
- "cell_type": "code",
- "source": [
- "california_housing_dataframe.head()"
- ],
- "execution_count": 6,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "| \n", - " | longitude | \n", - "latitude | \n", - "housing_median_age | \n", - "total_rooms | \n", - "total_bedrooms | \n", - "population | \n", - "households | \n", - "median_income | \n", - "median_house_value | \n", - "
|---|---|---|---|---|---|---|---|---|---|
| count | \n", - "17000.000000 | \n", - "17000.000000 | \n", - "17000.000000 | \n", - "17000.000000 | \n", - "17000.000000 | \n", - "17000.000000 | \n", - "17000.000000 | \n", - "17000.000000 | \n", - "17000.000000 | \n", - "
| mean | \n", - "-119.562108 | \n", - "35.625225 | \n", - "28.589353 | \n", - "2643.664412 | \n", - "539.410824 | \n", - "1429.573941 | \n", - "501.221941 | \n", - "3.883578 | \n", - "207300.912353 | \n", - "
| std | \n", - "2.005166 | \n", - "2.137340 | \n", - "12.586937 | \n", - "2179.947071 | \n", - "421.499452 | \n", - "1147.852959 | \n", - "384.520841 | \n", - "1.908157 | \n", - "115983.764387 | \n", - "
| min | \n", - "-124.350000 | \n", - "32.540000 | \n", - "1.000000 | \n", - "2.000000 | \n", - "1.000000 | \n", - "3.000000 | \n", - "1.000000 | \n", - "0.499900 | \n", - "14999.000000 | \n", - "
| 25% | \n", - "-121.790000 | \n", - "33.930000 | \n", - "18.000000 | \n", - "1462.000000 | \n", - "297.000000 | \n", - "790.000000 | \n", - "282.000000 | \n", - "2.566375 | \n", - "119400.000000 | \n", - "
| 50% | \n", - "-118.490000 | \n", - "34.250000 | \n", - "29.000000 | \n", - "2127.000000 | \n", - "434.000000 | \n", - "1167.000000 | \n", - "409.000000 | \n", - "3.544600 | \n", - "180400.000000 | \n", - "
| 75% | \n", - "-118.000000 | \n", - "37.720000 | \n", - "37.000000 | \n", - "3151.250000 | \n", - "648.250000 | \n", - "1721.000000 | \n", - "605.250000 | \n", - "4.767000 | \n", - "265000.000000 | \n", - "
| max | \n", - "-114.310000 | \n", - "41.950000 | \n", - "52.000000 | \n", - "37937.000000 | \n", - "6445.000000 | \n", - "35682.000000 | \n", - "6082.000000 | \n", - "15.000100 | \n", - "500001.000000 | \n", - "
\n",
- "\n",
- "\n",
- " \n",
- "
\n",
- "
"
- ],
- "text/plain": [
- " longitude latitude housing_median_age total_rooms total_bedrooms \\\n",
- "0 -114.31 34.19 15.0 5612.0 1283.0 \n",
- "1 -114.47 34.40 19.0 7650.0 1901.0 \n",
- "2 -114.56 33.69 17.0 720.0 174.0 \n",
- "3 -114.57 33.64 14.0 1501.0 337.0 \n",
- "4 -114.57 33.57 20.0 1454.0 326.0 \n",
- "\n",
- " population households median_income median_house_value \n",
- "0 1015.0 472.0 1.4936 66900.0 \n",
- "1 1129.0 463.0 1.8200 80100.0 \n",
- "2 333.0 117.0 1.6509 85700.0 \n",
- "3 515.0 226.0 3.1917 73400.0 \n",
- "4 624.0 262.0 1.9250 65500.0 "
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 6
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "w9-Es5Y6laGd"
- },
- "cell_type": "markdown",
- "source": [
- "Another powerful feature of *pandas* is graphing. For example, `DataFrame.hist` lets you quickly study the distribution of values in a column:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "nqndFVXVlbPN",
- "outputId": "425c7814-fb16-441b-b529-912371ca3f57",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 395
- }
- },
- "cell_type": "code",
- "source": [
- "california_housing_dataframe.hist('housing_median_age')"
- ],
- "execution_count": 7,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "array([[| \n", - " | longitude | \n", - "latitude | \n", - "housing_median_age | \n", - "total_rooms | \n", - "total_bedrooms | \n", - "population | \n", - "households | \n", - "median_income | \n", - "median_house_value | \n", - "
|---|---|---|---|---|---|---|---|---|---|
| 0 | \n", - "-114.31 | \n", - "34.19 | \n", - "15.0 | \n", - "5612.0 | \n", - "1283.0 | \n", - "1015.0 | \n", - "472.0 | \n", - "1.4936 | \n", - "66900.0 | \n", - "
| 1 | \n", - "-114.47 | \n", - "34.40 | \n", - "19.0 | \n", - "7650.0 | \n", - "1901.0 | \n", - "1129.0 | \n", - "463.0 | \n", - "1.8200 | \n", - "80100.0 | \n", - "
| 2 | \n", - "-114.56 | \n", - "33.69 | \n", - "17.0 | \n", - "720.0 | \n", - "174.0 | \n", - "333.0 | \n", - "117.0 | \n", - "1.6509 | \n", - "85700.0 | \n", - "
| 3 | \n", - "-114.57 | \n", - "33.64 | \n", - "14.0 | \n", - "1501.0 | \n", - "337.0 | \n", - "515.0 | \n", - "226.0 | \n", - "3.1917 | \n", - "73400.0 | \n", - "
| 4 | \n", - "-114.57 | \n", - "33.57 | \n", - "20.0 | \n", - "1454.0 | \n", - "326.0 | \n", - "624.0 | \n", - "262.0 | \n", - "1.9250 | \n", - "65500.0 | \n", - "
"
- ]
- },
- "metadata": {
- "tags": []
- }
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "XtYZ7114n3b-"
- },
- "cell_type": "markdown",
- "source": [
- "## Accessing Data\n",
- "\n",
- "You can access `DataFrame` data using familiar Python dict/list operations:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "_TFm7-looBFF",
- "outputId": "d7ab8f7b-e1e3-480c-a6f5-be3cf05dfc37",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 100
- }
- },
- "cell_type": "code",
- "source": [
- "cities = pd.DataFrame({ 'City name': city_names, 'Population': population })\n",
- "print(type(cities['City name']))\n",
- "cities['City name']"
- ],
- "execution_count": 8,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "\n"
- ],
- "name": "stdout"
- },
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "0 San Francisco\n",
- "1 San Jose\n",
- "2 Sacramento\n",
- "Name: City name, dtype: object"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 8
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "V5L6xacLoxyv",
- "outputId": "1319d6e2-f41e-4a35-a0ad-7ead83684577",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 50
- }
- },
- "cell_type": "code",
- "source": [
- "print(type(cities['City name'][1]))\n",
- "cities['City name'][1]"
- ],
- "execution_count": 9,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "\n"
- ],
- "name": "stdout"
- },
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "'San Jose'"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 9
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "gcYX1tBPugZl",
- "outputId": "927153f2-e74a-4256-ad8d-b6211ad065b9",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 124
- }
- },
- "cell_type": "code",
- "source": [
- "print(type(cities[0:2]))\n",
- "cities[0:2]"
- ],
- "execution_count": 10,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "\n"
- ],
- "name": "stdout"
- },
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "
\n",
- "\n",
- "\n",
- " \n",
- "
\n",
- "
"
- ],
- "text/plain": [
- " City name Population\n",
- "0 San Francisco 852469\n",
- "1 San Jose 1015785"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 10
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "65g1ZdGVjXsQ"
- },
- "cell_type": "markdown",
- "source": [
- "In addition, *pandas* provides an extremely rich API for advanced [indexing and selection](http://pandas.pydata.org/pandas-docs/stable/indexing.html) that is too extensive to be covered here."
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "RM1iaD-ka3Y1"
- },
- "cell_type": "markdown",
- "source": [
- "## Manipulating Data\n",
- "\n",
- "You may apply Python's basic arithmetic operations to `Series`. For example:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "XWmyCFJ5bOv-",
- "outputId": "91280582-c473-48cd-c7f5-36a8a73df7e9",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 84
- }
- },
- "cell_type": "code",
- "source": [
- "population / 1000."
- ],
- "execution_count": 11,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "0 852.469\n",
- "1 1015.785\n",
- "2 485.199\n",
- "dtype: float64"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 11
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "TQzIVnbnmWGM"
- },
- "cell_type": "markdown",
- "source": [
- "[NumPy](http://www.numpy.org/) is a popular toolkit for scientific computing. *pandas* `Series` can be used as arguments to most NumPy functions:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "ko6pLK6JmkYP",
- "outputId": "92b5b7fd-95be-4fc5-8033-5b8da8b2a95b",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 84
- }
- },
- "cell_type": "code",
- "source": [
- "import numpy as np\n",
- "\n",
- "np.log(population)"
- ],
- "execution_count": 12,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "0 13.655892\n",
- "1 13.831172\n",
- "2 13.092314\n",
- "dtype: float64"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 12
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "xmxFuQmurr6d"
- },
- "cell_type": "markdown",
- "source": [
- "For more complex single-column transformations, you can use `Series.apply`. Like the Python [map function](https://docs.python.org/2/library/functions.html#map), \n",
- "`Series.apply` accepts as an argument a [lambda function](https://docs.python.org/2/tutorial/controlflow.html#lambda-expressions), which is applied to each value.\n",
- "\n",
- "The example below creates a new `Series` that indicates whether `population` is over one million:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "Fc1DvPAbstjI",
- "outputId": "e447f694-479c-4964-fa8e-4e5bfebad9cc",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 84
- }
- },
- "cell_type": "code",
- "source": [
- "population.apply(lambda val: val > 1000000)"
- ],
- "execution_count": 13,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "0 False\n",
- "1 True\n",
- "2 False\n",
- "dtype: bool"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 13
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "ZeYYLoV9b9fB"
- },
- "cell_type": "markdown",
- "source": [
- "\n",
- "Modifying `DataFrames` is also straightforward. For example, the following code adds two `Series` to an existing `DataFrame`:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "0gCEX99Hb8LR",
- "outputId": "7d96cf32-a00a-4c43-81d1-88953ab65041",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 137
- }
- },
- "cell_type": "code",
- "source": [
- "cities['Area square miles'] = pd.Series([46.87, 176.53, 97.92])\n",
- "cities['Population density'] = cities['Population'] / cities['Area square miles']\n",
- "cities"
- ],
- "execution_count": 14,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "| \n", - " | City name | \n", - "Population | \n", - "
|---|---|---|
| 0 | \n", - "San Francisco | \n", - "852469 | \n", - "
| 1 | \n", - "San Jose | \n", - "1015785 | \n", - "
\n",
- "\n",
- "\n",
- " \n",
- "
\n",
- "
"
- ],
- "text/plain": [
- " City name Population Area square miles Population density\n",
- "0 San Francisco 852469 46.87 18187.945381\n",
- "1 San Jose 1015785 176.53 5754.177760\n",
- "2 Sacramento 485199 97.92 4955.055147"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 14
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "6qh63m-ayb-c"
- },
- "cell_type": "markdown",
- "source": [
- "## Exercise #1\n",
- "\n",
- "Modify the `cities` table by adding a new boolean column that is True if and only if *both* of the following are True:\n",
- "\n",
- " * The city is named after a saint.\n",
- " * The city has an area greater than 50 square miles.\n",
- "\n",
- "**Note:** Boolean `Series` are combined using the bitwise, rather than the traditional boolean, operators. For example, when performing *logical and*, use `&` instead of `and`.\n",
- "\n",
- "**Hint:** \"San\" in Spanish means \"saint.\""
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "zCOn8ftSyddH",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 137
- },
- "outputId": "508be6c9-95f2-432c-be0a-e2f2d24e8886"
- },
- "cell_type": "code",
- "source": [
- "# Your code here\n",
- "cities['Wide and has saint name'] = (cities['Area square miles'] > 50) & cities['City name'].apply(lambda name: name.startswith('San'))\n",
- "cities"
- ],
- "execution_count": 15,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "| \n", - " | City name | \n", - "Population | \n", - "Area square miles | \n", - "Population density | \n", - "
|---|---|---|---|---|
| 0 | \n", - "San Francisco | \n", - "852469 | \n", - "46.87 | \n", - "18187.945381 | \n", - "
| 1 | \n", - "San Jose | \n", - "1015785 | \n", - "176.53 | \n", - "5754.177760 | \n", - "
| 2 | \n", - "Sacramento | \n", - "485199 | \n", - "97.92 | \n", - "4955.055147 | \n", - "
\n",
- "\n",
- "\n",
- " \n",
- "
\n",
- "
"
- ],
- "text/plain": [
- " City name Population Area square miles Population density \\\n",
- "0 San Francisco 852469 46.87 18187.945381 \n",
- "1 San Jose 1015785 176.53 5754.177760 \n",
- "2 Sacramento 485199 97.92 4955.055147 \n",
- "\n",
- " Wide and has saint name \n",
- "0 False \n",
- "1 True \n",
- "2 False "
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 15
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "YHIWvc9Ms-Ll"
- },
- "cell_type": "markdown",
- "source": [
- "### Solution\n",
- "\n",
- "Click below for a solution."
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "T5OlrqtdtCIb",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "cities['Is wide and has saint name'] = (cities['Area square miles'] > 50) & cities['City name'].apply(lambda name: name.startswith('San'))\n",
- "cities"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "f-xAOJeMiXFB"
- },
- "cell_type": "markdown",
- "source": [
- "## Indexes\n",
- "Both `Series` and `DataFrame` objects also define an `index` property that assigns an identifier value to each `Series` item or `DataFrame` row. \n",
- "\n",
- "By default, at construction, *pandas* assigns index values that reflect the ordering of the source data. Once created, the index values are stable; that is, they do not change when data is reordered."
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "2684gsWNinq9",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 33
- },
- "outputId": "11071fbe-39ca-482f-b66f-e3a7e7e28996"
- },
- "cell_type": "code",
- "source": [
- "city_names.index"
- ],
- "execution_count": 16,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "RangeIndex(start=0, stop=3, step=1)"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 16
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "F_qPe2TBjfWd",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 33
- },
- "outputId": "42bb63a5-5a3c-494a-8d99-b324a91dea7c"
- },
- "cell_type": "code",
- "source": [
- "cities.index"
- ],
- "execution_count": 17,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "RangeIndex(start=0, stop=3, step=1)"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 17
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "hp2oWY9Slo_h"
- },
- "cell_type": "markdown",
- "source": [
- "Call `DataFrame.reindex` to manually reorder the rows. For example, the following has the same effect as sorting by city name:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "sN0zUzSAj-U1",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 137
- },
- "outputId": "6f05c626-0057-43e2-d444-e6c50622ac44"
- },
- "cell_type": "code",
- "source": [
- "cities.reindex([2, 0, 1])"
- ],
- "execution_count": 18,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "| \n", - " | City name | \n", - "Population | \n", - "Area square miles | \n", - "Population density | \n", - "Wide and has saint name | \n", - "
|---|---|---|---|---|---|
| 0 | \n", - "San Francisco | \n", - "852469 | \n", - "46.87 | \n", - "18187.945381 | \n", - "False | \n", - "
| 1 | \n", - "San Jose | \n", - "1015785 | \n", - "176.53 | \n", - "5754.177760 | \n", - "True | \n", - "
| 2 | \n", - "Sacramento | \n", - "485199 | \n", - "97.92 | \n", - "4955.055147 | \n", - "False | \n", - "
\n",
- "\n",
- "\n",
- " \n",
- "
\n",
- "
"
- ],
- "text/plain": [
- " City name Population Area square miles Population density \\\n",
- "2 Sacramento 485199 97.92 4955.055147 \n",
- "0 San Francisco 852469 46.87 18187.945381 \n",
- "1 San Jose 1015785 176.53 5754.177760 \n",
- "\n",
- " Wide and has saint name \n",
- "2 False \n",
- "0 False \n",
- "1 True "
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 18
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "-GQFz8NZuS06"
- },
- "cell_type": "markdown",
- "source": [
- "Reindexing is a great way to shuffle (randomize) a `DataFrame`. In the example below, we take the index, which is array-like, and pass it to NumPy's `random.permutation` function, which shuffles its values in place. Calling `reindex` with this shuffled array causes the `DataFrame` rows to be shuffled in the same way.\n",
- "Try running the following cell multiple times!"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "mF8GC0k8uYhz",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 137
- },
- "outputId": "5496dd16-e56e-4b2d-a68c-039690cb4a57"
- },
- "cell_type": "code",
- "source": [
- "cities.reindex(np.random.permutation(cities.index))"
- ],
- "execution_count": 24,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "| \n", - " | City name | \n", - "Population | \n", - "Area square miles | \n", - "Population density | \n", - "Wide and has saint name | \n", - "
|---|---|---|---|---|---|
| 2 | \n", - "Sacramento | \n", - "485199 | \n", - "97.92 | \n", - "4955.055147 | \n", - "False | \n", - "
| 0 | \n", - "San Francisco | \n", - "852469 | \n", - "46.87 | \n", - "18187.945381 | \n", - "False | \n", - "
| 1 | \n", - "San Jose | \n", - "1015785 | \n", - "176.53 | \n", - "5754.177760 | \n", - "True | \n", - "
\n",
- "\n",
- "\n",
- " \n",
- "
\n",
- "
"
- ],
- "text/plain": [
- " City name Population Area square miles Population density \\\n",
- "2 Sacramento 485199 97.92 4955.055147 \n",
- "0 San Francisco 852469 46.87 18187.945381 \n",
- "1 San Jose 1015785 176.53 5754.177760 \n",
- "\n",
- " Wide and has saint name \n",
- "2 False \n",
- "0 False \n",
- "1 True "
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 24
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "fSso35fQmGKb"
- },
- "cell_type": "markdown",
- "source": [
- "For more information, see the [Index documentation](http://pandas.pydata.org/pandas-docs/stable/indexing.html#index-objects)."
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "8UngIdVhz8C0"
- },
- "cell_type": "markdown",
- "source": [
- "## Exercise #2\n",
- "\n",
- "The `reindex` method allows index values that are not in the original `DataFrame`'s index values. Try it and see what happens if you use such values! Why do you think this is allowed?"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "PN55GrDX0jzO",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 166
- },
- "outputId": "37aab3dd-e4b4-4afe-8bdb-52da45962509"
- },
- "cell_type": "code",
- "source": [
- "# Your code here\n",
- "cities.reindex([2, 0, 1, 4])"
- ],
- "execution_count": 25,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/html": [
- "| \n", - " | City name | \n", - "Population | \n", - "Area square miles | \n", - "Population density | \n", - "Wide and has saint name | \n", - "
|---|---|---|---|---|---|
| 2 | \n", - "Sacramento | \n", - "485199 | \n", - "97.92 | \n", - "4955.055147 | \n", - "False | \n", - "
| 0 | \n", - "San Francisco | \n", - "852469 | \n", - "46.87 | \n", - "18187.945381 | \n", - "False | \n", - "
| 1 | \n", - "San Jose | \n", - "1015785 | \n", - "176.53 | \n", - "5754.177760 | \n", - "True | \n", - "
\n",
- "\n",
- "\n",
- " \n",
- "
\n",
- "
"
- ],
- "text/plain": [
- " City name Population Area square miles Population density \\\n",
- "2 Sacramento 485199.0 97.92 4955.055147 \n",
- "0 San Francisco 852469.0 46.87 18187.945381 \n",
- "1 San Jose 1015785.0 176.53 5754.177760 \n",
- "4 NaN NaN NaN NaN \n",
- "\n",
- " Wide and has saint name \n",
- "2 False \n",
- "0 False \n",
- "1 True \n",
- "4 NaN "
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 25
- }
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "TJffr5_Jwqvd"
- },
- "cell_type": "markdown",
- "source": [
- "### Solution\n",
- "\n",
- "Click below for the solution."
- ]
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "8oSvi2QWwuDH"
- },
- "cell_type": "markdown",
- "source": [
- "If your `reindex` input array includes values not in the original `DataFrame` index values, `reindex` will add new rows for these \"missing\" indices and populate all corresponding columns with `NaN` values:"
- ]
- },
- {
- "metadata": {
- "colab_type": "code",
- "id": "yBdkucKCwy4x",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "cities.reindex([0, 4, 5, 2])"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "colab_type": "text",
- "id": "2l82PhPbwz7g"
- },
- "cell_type": "markdown",
- "source": [
- "This behavior is desirable because indexes are often strings pulled from the actual data (see the [*pandas* reindex\n",
- "documentation](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.reindex.html) for an example\n",
- "in which the index values are browser names).\n",
- "\n",
- "In this case, allowing \"missing\" indices makes it easy to reindex using an external list, as you don't have to worry about\n",
- "sanitizing the input."
- ]
- }
- ]
-}
\ No newline at end of file
| \n", - " | City name | \n", - "Population | \n", - "Area square miles | \n", - "Population density | \n", - "Wide and has saint name | \n", - "
|---|---|---|---|---|---|
| 2 | \n", - "Sacramento | \n", - "485199.0 | \n", - "97.92 | \n", - "4955.055147 | \n", - "False | \n", - "
| 0 | \n", - "San Francisco | \n", - "852469.0 | \n", - "46.87 | \n", - "18187.945381 | \n", - "False | \n", - "
| 1 | \n", - "San Jose | \n", - "1015785.0 | \n", - "176.53 | \n", - "5754.177760 | \n", - "True | \n", - "
| 4 | \n", - "NaN | \n", - "NaN | \n", - "NaN | \n", - "NaN | \n", - "NaN | \n", - "