diff --git a/First_Date_with_TensorFlow.ipynb b/First_Date_with_TensorFlow.ipynb
new file mode 100644
index 0000000..5f48763
--- /dev/null
+++ b/First_Date_with_TensorFlow.ipynb
@@ -0,0 +1,924 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "name": "First_Date_with_TensorFlow.ipynb",
+ "version": "0.3.2",
+ "provenance": [],
+ "include_colab_link": true
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ }
+ },
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ " "
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
\n",
+ "\n",
+ "You know what's important for understanding Deep Learning / Machine Learning?
\n",
+ "Intuition. Period.\n",
+ "\n",
+ "And Intuition comes when you run the code multiple times.\n",
+ "\n",
+ "So, today I can write a couple of defination and say this is this, this is that.
\n",
+ "You Google half of the things up. You find answers which you need to Google further.
\n",
+ "In the process, you probably won't even remember what's the first thing you started out with!\n",
+ "\n",
+ "So?\n",
+ "\n",
+ "Hence on, I will execute cells with code.
\n",
+ "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
+ "**No Theory Just Code.**\n",
+ "\n",
+ "I will at max give a defination that extends for a line. That's it.
\n",
+ "Let's get started!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "**RECOMMENDED!**
\n",
+ "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
+ "Don't just `shift+enter` the cells.\n",
+ "\n",
+ "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "gYWUpE-bYKWP",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Essential imports\n",
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "eKpz5NCIYMdi",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define some tensors\n",
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
+ " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "vmMcjzTxbWzw",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 72
+ },
+ "outputId": "34cf1bfa-8aa4-4d12-aef3-99f05b031d47"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's print them out!\n",
+ "print (t1)\n",
+ "print (t2)\n",
+ "print (t3)"
+ ],
+ "execution_count": 4,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_1:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_2:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "10ahnfjYbcop",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Where's Waldo?
\n",
+ "I mean, the value?
\n",
+ "\n",
+ "So, the thing is you can't print the value of tensors directly.
\n",
+ "You have to use `session`, so let's do that!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ol6O5I7Tb2nb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 219
+ },
+ "outputId": "bf5289a8-fc50-4115-c8ea-da468e7d1e2a"
+ },
+ "cell_type": "code",
+ "source": [
+ "sess = tf.Session()\n",
+ "print (sess.run(t1))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t2))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t3))\n",
+ "sess.close()"
+ ],
+ "execution_count": 5,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "rXKfVs_zb-kU",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Aaahaa!! Just printed those tensors!!!
\n",
+ "Feels good!
\n",
+ "\n",
+ "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
+ "And you are still using the markdown cells for the theory ?!\n",
+ "\n",
+ "I am just gonna say I am a unreasonable man.
\n",
+ "\n",
+ "\n",
+ "So, you are programming with tf.
\n",
+ "What ever you do is broken down to 2 basic steps:\n",
+ "- Building the computational Graph!\n",
+ "- Execute that graph using `session`!\n",
+ "\n",
+ "That's all!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Let's compare this 2 steps with what we did above!
\n",
+ "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
+ "And then I executed each tensor in this graph using a `session`.\n",
+ "\n",
+ "That simple!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Now, let's define a few more computational graphs and execute them with sessions.\n",
+ "\n",
+ "Okay, to start with let's build this computational graph!\n",
+ "\n",
+ "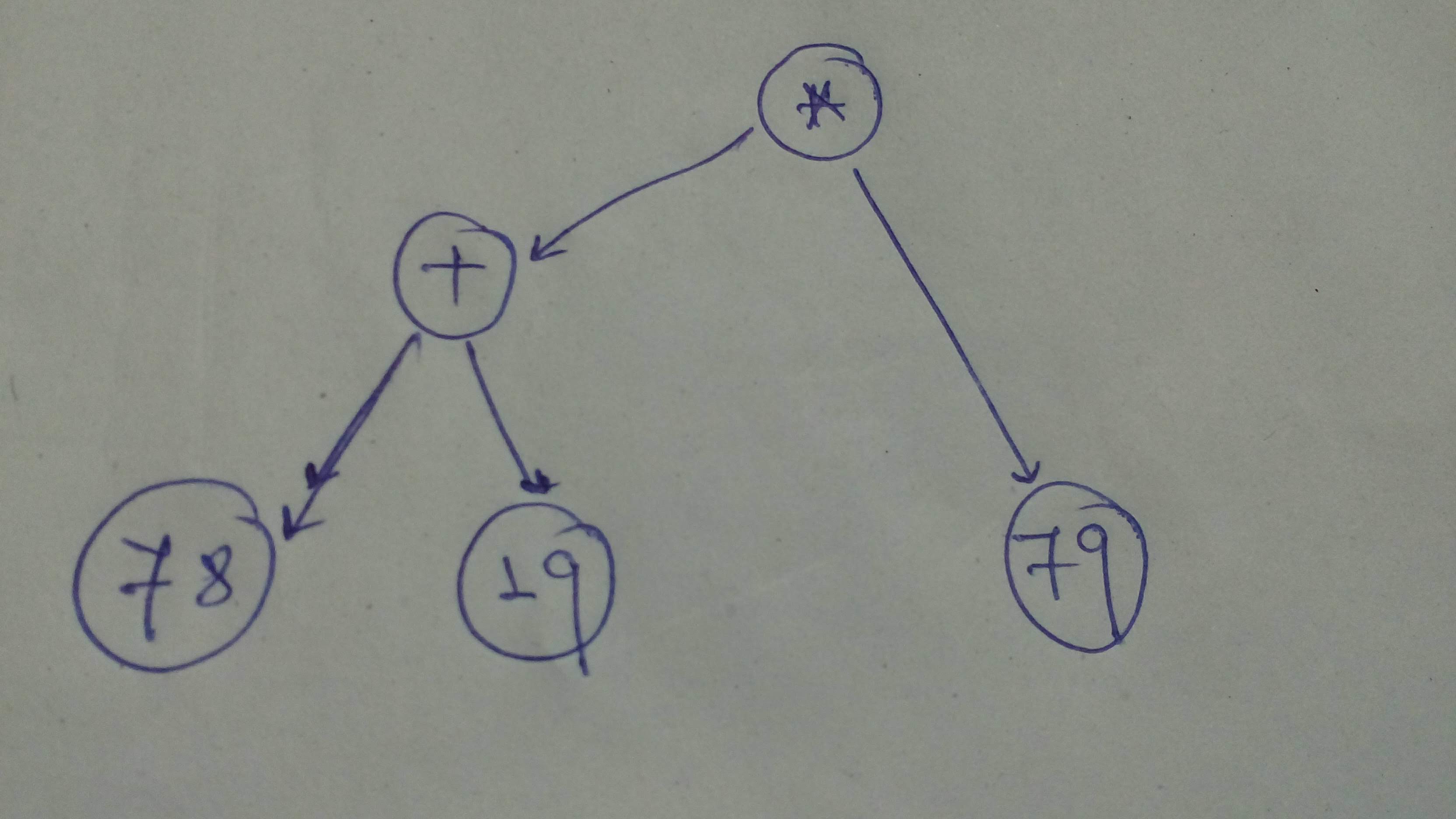"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "FyVz0GNqgreZ",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 54
+ },
+ "outputId": "591ecce1-a550-4339-bdc9-7be02558699e"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the graph\n",
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "\n",
+ "# Alternatively\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "\n",
+ "# Let's execute using session\n",
+ "sess = tf.Session()\n",
+ "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
+ "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
+ "sess.close()"
+ ],
+ "execution_count": 6,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "SVMMtuFYhaQB",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's define a sligtly more involved graph!\n",
+ "\n",
+ "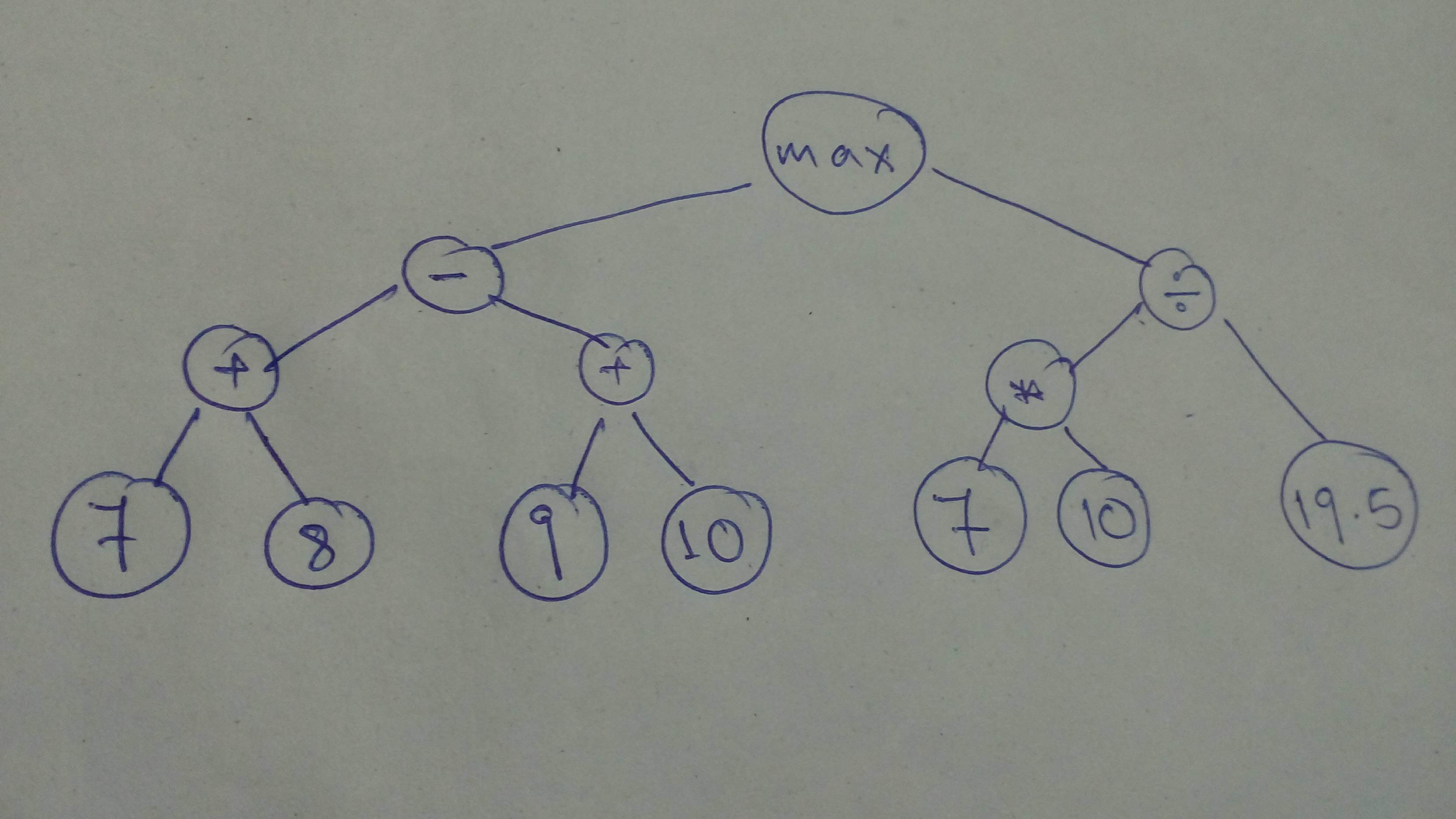"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4856BTvRhiBb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 72
+ },
+ "outputId": "12286d9a-3e05-4672-d9c8-fdd1af92fbd7"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let build the graph\n",
+ "# We need to cast cause the tensors operated on should be of the same type\n",
+ "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
+ " dtype=tf.float32)\n",
+ "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
+ "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "# Let's execute\n",
+ "sess = tf.Session()\n",
+ "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', part1_res)\n",
+ "print ('Part 2 Result: ', part2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 7,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "B-_ZDtEbj4N0",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Cool! Let's go! Build another graph and execute it with sessions.
\n",
+ "\n",
+ "But this time, it's all you!\n",
+ "\n",
+ "Build this graph and execute it with `session`!\n",
+ "\n",
+ "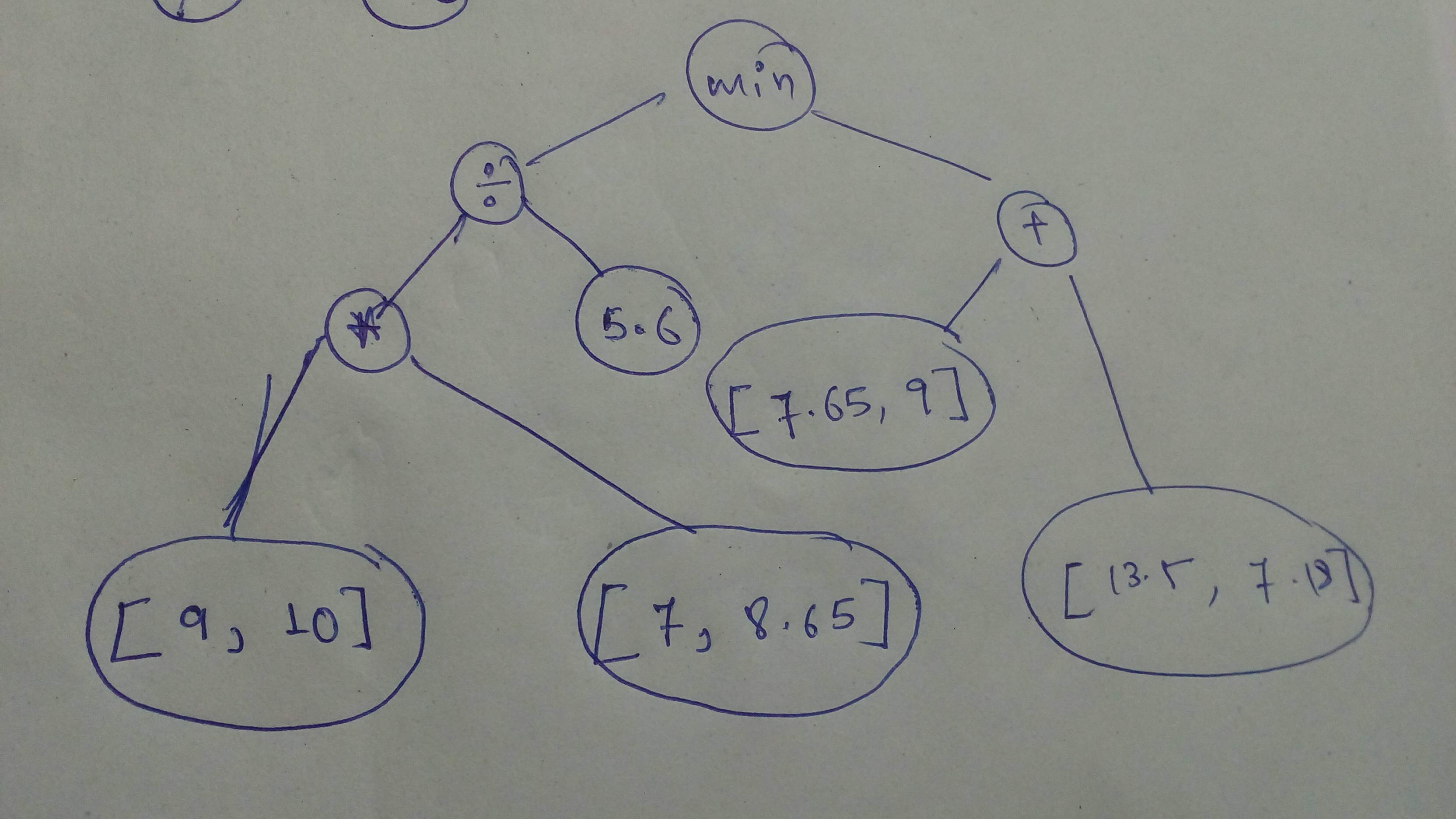\n",
+ "\n",
+ "_Remember that `tensors` operated on should be of the same type!_
\n",
+ "_Search up errors and other help you need on Google_"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "-uHNe1BolJY0",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 35
+ },
+ "outputId": "a1cfa3b0-de03-4d26-94fb-a938632eae79"
+ },
+ "cell_type": "code",
+ "source": [
+ "a=tf.constant([9,10],dtype=tf.float32)\n",
+ "b=tf.constant([7,8.65],dtype=tf.float32)\n",
+ "c=tf.constant(5.6,dtype=tf.float32)\n",
+ "d=tf.constant([7.65,9],dtype=tf.float32)\n",
+ "e=tf.constant([13.5,7.18],dtype=tf.float32)\n",
+ "\n",
+ "result=tf.minimum(tf.divide(tf.multiply(a,b),c),tf.add(d,e))\n",
+ "sess=tf.Session()\n",
+ "\n",
+ "print(sess.run(result))"
+ ],
+ "execution_count": 9,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[11.25 15.446429]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "qmap38WelREN",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's do another!
\n",
+ "It's fun! Isn't it?!\n",
+ "\n",
+ "Build and execute this one!\n",
+ "\n",
+ "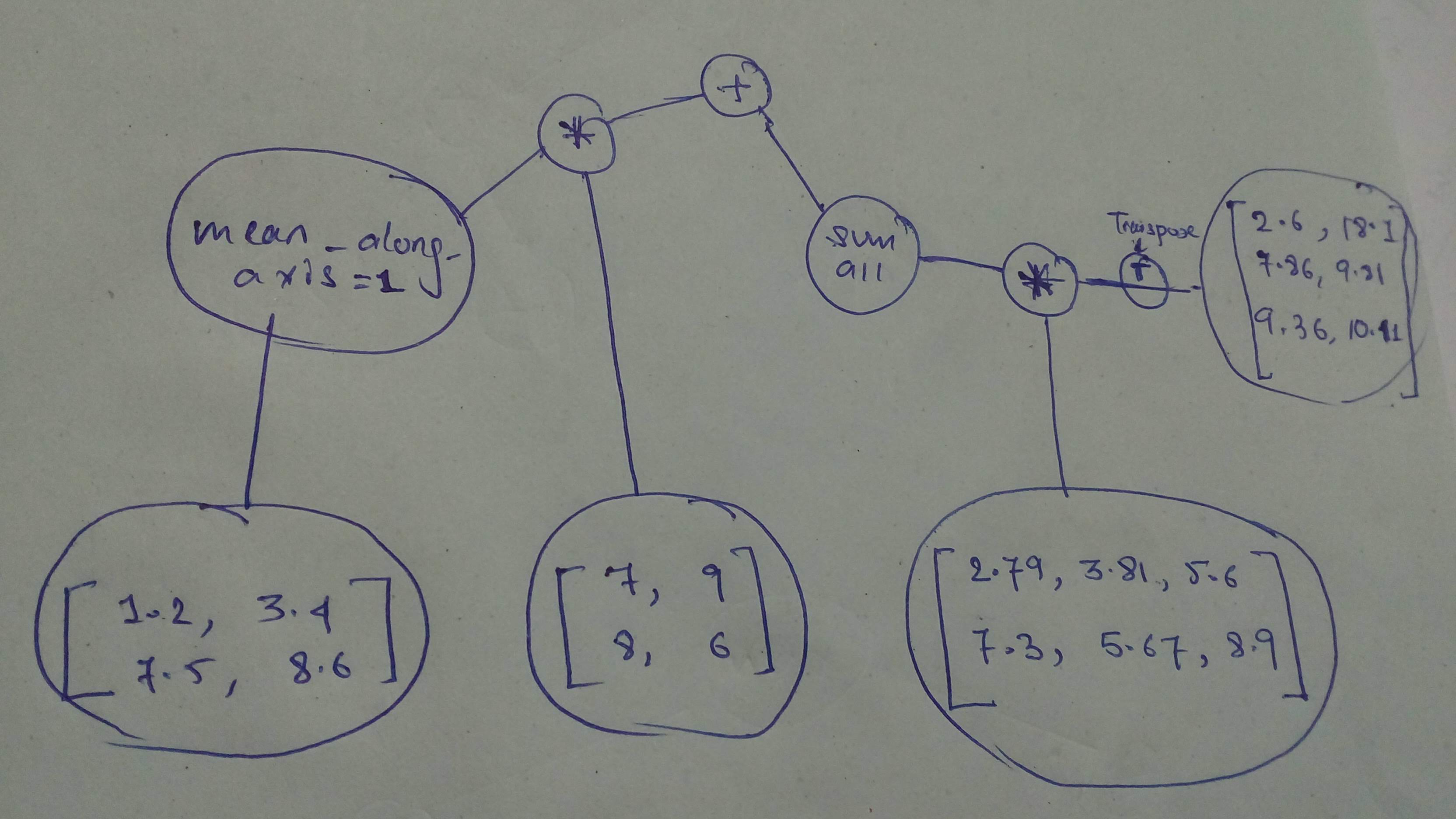"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "0ZhYwAlLmEvB",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 54
+ },
+ "outputId": "97e40ecb-efae-434d-fb93-043d89b9d349"
+ },
+ "cell_type": "code",
+ "source": [
+ "a=tf.constant([[1.2,3.4],[7.5,8.6]],dtype=tf.float32)\n",
+ "b=tf.constant([[7,9],[8,6]],dtype=tf.float32)\n",
+ "c=tf.constant([[2.79,3.81,5.6],[7.3,5.67,8.9]],dtype=tf.float32)\n",
+ "d=tf.constant([[2.6,18.1],[7.86,9.81],[9.36,10.11]],dtype=tf.float32)\n",
+ "result=tf.add(tf.multiply(tf.reduce_mean(a,1),b),tf.reduce_sum(tf.multiply(tf.transpose(d),c)))\n",
+ "print(sess.run(result))"
+ ],
+ "execution_count": 10,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[[383.4483 439.7983 ]\n",
+ " [385.7483 415.64832]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "BnB0b6qCmGmg",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "And a final one, before we move on to the next part!\n",
+ "\n",
+ "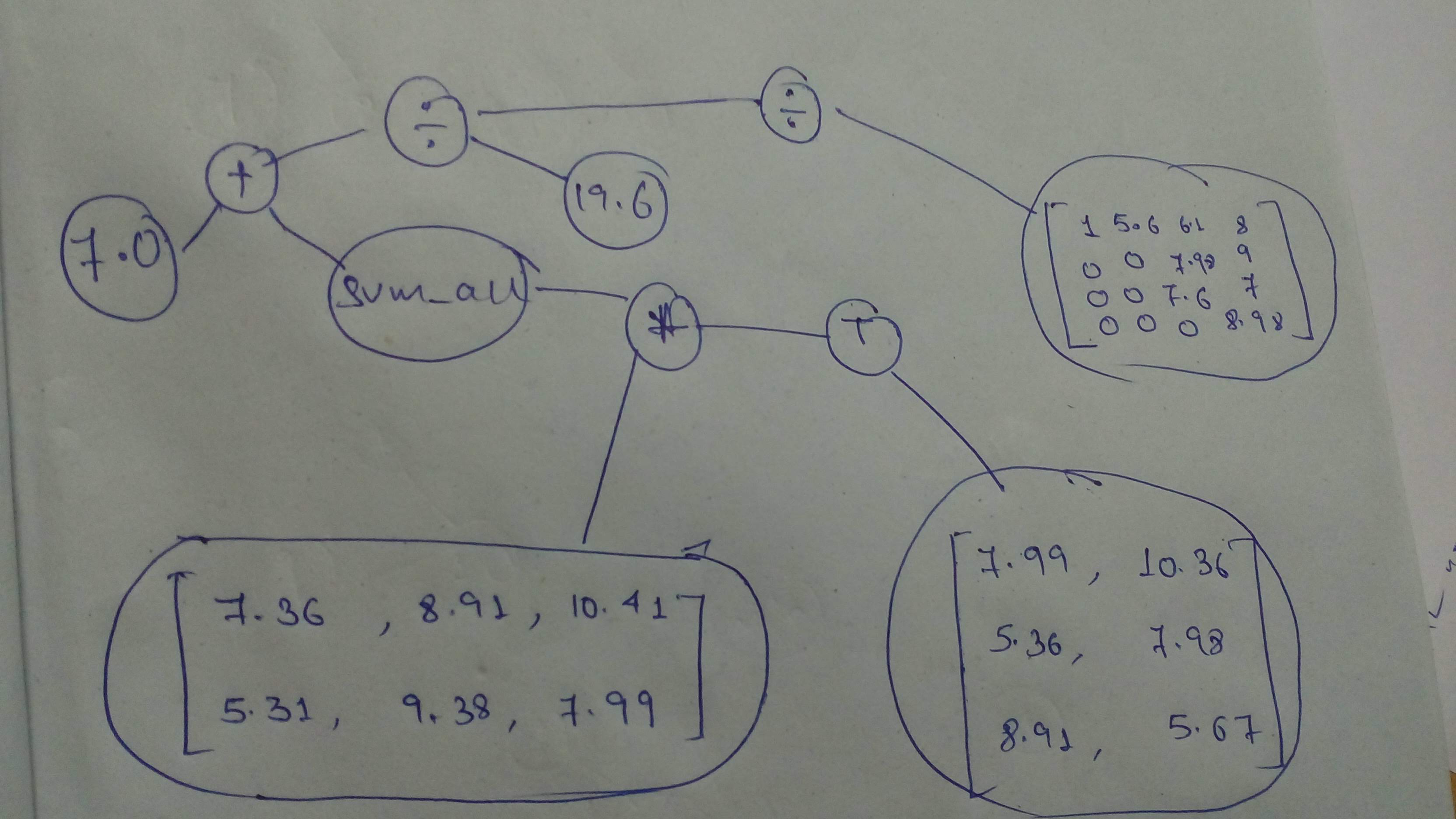"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "GQWyCvsQmMcL",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 90
+ },
+ "outputId": "58f3a537-010c-4fad-bf58-fd1a3e52f6d0"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "a=tf.constant([[7.36,8.91,10.41],[5.31,9.38,7.99]],dtype=tf.float32)\n",
+ "b=tf.constant([[7.99,10.36],[5.36,7.98],[8.91,5.67]],dtype=tf.float32)\n",
+ "c=tf.constant([[1,5.6,6.1,8],[0,0,7.98,9],[0,0,7.6,7],[0,0,0,8.98]],dtype=tf.float32)\n",
+ "result=tf.divide(tf.divide(tf.add(tf.reduce_sum(tf.multiply(a,tf.transpose(b))),7.0),19.6),c)\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "print(sess.run(result))"
+ ],
+ "execution_count": 11,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[[19.463488 3.475623 3.1907358 2.432936 ]\n",
+ " [ inf inf 2.4390335 2.1626098]\n",
+ " [ inf inf 2.5609853 2.7804983]\n",
+ " [ inf inf inf 2.1674263]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "12NC7XTPsJw7",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# Linear Regression\n",
+ "\n",
+ "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
+ "\n",
+ "\n",
+ "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hW31RZkjtNwI",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Create the dataset\n",
+ "X = np.linspace(-30.0, 300.0, 300)\n",
+ "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Normalize the dataset\n",
+ "X = X / np.max(X)\n",
+ "Y = Y / np.max(Y)\n",
+ "\n",
+ "# Divide it into train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "LQKy6U33y4lt",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the hyperparameters\n",
+ "learning_rate = 0.00001\n",
+ "n_epochs = 60\n",
+ "interval = 20"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "1h1-D8K1uT48",
+ "colab_type": "code",
+ "outputId": "10ce1cd9-1a8e-4737-9145-fd898929d9ce",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 347
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# let's viz the first 10 datapoints of the dataset\n",
+ "plt.plot(train_X[:10], train_Y[:10], 'g')\n",
+ "plt.show()"
+ ],
+ "execution_count": 14,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFKCAYAAADmCN3IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3XlcVXX+x/EXO6hgYKA2uaS5tGEu\niEJoOlFqU2MlJjNiljNTalppk4QmWZpoYsZoC2nmOKYjTVOOGVpJloIrDVrzU9vMBcNLociiLPf8\n/jCZGFPweuHc5f18PHrUPfeccz+fTva+537POV8PwzAMRERExCl5ml2AiIiI2E5BLiIi4sQU5CIi\nIk5MQS4iIuLEFOQiIiJOTEEuIiLixLzNLsAWFstJu+8zOLgJRUVldt+vI1PP7sEdewb37Fs9u7bQ\n0MBfXK4z8p94e3uZXUKjU8/uwR17BvfsWz27JwW5iIiIE1OQi4iIODEFuYiIiBNTkIuIiDgxBbmI\niIgTU5CLiIg4MZvuI6+srCQxMZH8/Hy8vLyYPXs2bdq0qbXOmjVrWLZsGZ6engwfPpy4uDgKCgpI\nSkqioqICq9XKk08+yfXXX8/AgQNp1aoVXl5nbiOYN28eLVu2vPTuREREXJxNQb527VqCgoJITU1l\n8+bNpKamsmDBgpr3y8rKWLRoEW+99RY+Pj4MGzaM2NhY3njjDWJjYxkxYgS5ubm88MILLFmyBIDX\nXnuNpk2b2qcrERERN2HTT+s5OTnExsYCEBUVRW5ubq338/LyuOGGGwgMDMTf358ePXqQm5tLcHAw\nx48fB6C4uJjg4OBLLF9ERMS92XRGXlhYSEhICACenp54eHhQUVGBr6/vOe8DhISEYLFYGD16NMOG\nDeOdd96hpKSElStX1qyTnJzMkSNH6NmzJ5MnT8bDw+O8nx8c3KRBnuZzvsffuTL17B7csWdwz77V\ns/upM8gzMjLIyMiotSwvL6/Wa8MwLriPs+8vXryYwYMHM3bsWLKyspgzZw4LFy5k4sSJxMTE0Lx5\nc8aPH8/69esZNGjQeffXEM/VDQ0NbJBnuDsy9ewe3LFncM++1bNjOFqSzyeHP+auTsPw9fK1235t\nftZ6XFwcq1evrvXXXXfdhcViAc5c+GYYRs3ZOEBYWBiFhYU1r48dO0ZYWBi5ubnExMQAEB0dzeef\nfw7A0KFDadGiBd7e3vTr14/9+/fb3qmIiIgJTlWdYsGuefR9sycTNj7Ef374vFE+16Yx8ujoaDIz\nMwHIysoiMjKy1vvdunVjz549FBcXU1paSm5uLr169aJdu3Y1Z/O7d++mXbt2nDx5kjFjxlBRUQHA\njh076NSp06X0JCIi0mgMw+D9b98jZlVvntv2DE18mvDigJe4MaxHo3y+TWPkQ4YMITs7m/j4eHx9\nfUlJSQEgPT2diIgIunfvzuTJkxkzZgweHh6MHz+ewMBAHnzwQaZOnVrzJWDq1KkEBgbSr18/7r33\nXvz8/Lj22msv+LO6iIiIo9j/4z6mbn6CTYez8Pb0Zmy3CUzu9QRBfs0brQYPo64BbgfUEOMhjjjO\n0tDUs3twx57BPftWz43nxOnjzNuRwpLP06myVjGgza+ZedMcOgV3brDPPN8YuU1n5CIiIu6o2lrN\nyr1/47ltMygsL6R90FU8e1MKt7YbdMG7rRqSglxERKQeth3dytTNT7Db8m+aeDdlWp+nebDbePy8\n/EytS0EuIiJyAUdL8nkmZzr/+HI1AMM638v0vs/Qqmlrkys7Q0EuIiLyC05VneLVvEW8sGseZVWl\ndAvtznMxc4loFVn3xo1IQS4iIvIzhmGw/sD7TN/yJAeKv+XygMuZddMc4q8ZiaeH400aqiAXERH5\nyf4f9zFtyxQ+PrQRb09vHuw2nsd7TaG532Vml3ZeCnIREXF7xadP8PzOFJbseZUqaxU3txnIzOg5\ndA7pYnZpdVKQi4iI27IaVlb+39+YtW0GheUW2gW159noFG5rP9i028kuloJcRETc0vaj25i6+Qny\nLJ/RxLspUyOTebDbePy9/c0u7aIoyEVExK18X3qUZ3Km89b+vwNwT6fhTO/7DK2bXWFyZbZRkIuI\niFs4XX2aV/MWMX/n85RVlRIeeiOzbppLZOs+Zpd2SRTkIiLi0gzDYMN3mTy1ObHmdrKZN6UQ33Uk\nXp5eZpd3yRTkIiLisr4s2s9TWxLZePBDvDy8eDB8HI9HJDr07WQXS0EuIiIup/j0CVJ3zuW1PS9T\nZa2i/5UDmHnTHLqEdDW7NLtTkIuIiMuwGlZW7V3BzK1PU1huoW1Qe56Nns2g9kOc5nayi6UgFxER\nl7Dz++1M3fwEnx3LpYl3E5Iip/NQt4ed7nayi6UgFxERp1ZQ+j3Pbk1m9b6VANzdKY7pfZ/hima/\nMrmyxqEgFxERp3S6+jRzNr/Es5/MpLSyhBsu78asmLn0ad3X7NIalYJcRESczgcHMpm2JZFvT3xD\nC/8WPBP9HL/rmuASt5NdLAW5iIg4ja+KvuSpLYl8dPADvDy8eCTyEcZfN4nL/IPNLs00CnIREXF4\nJyuKSd05l/TdL1FlrSLmypuZddMcYrr0xmI5aXZ5plKQi4iIw7IaVlbvW8mzOclYyo/RNrAdM6Kf\nY8hVv3HZ28kuloJcREQcktWwMnHjWFbvW0kT7yYk9p7G2BsnEOAdYHZpDkVBLiIiDscwDJ7anMjq\nfSvp2bIXi2/9K78KvNLsshySglxERBxO6s45vLbnFa4JuZY3b3+LYP8Qs0tyWJ5mFyAiIvJzi3e/\nwtwdz9E2qD2r73hHIV4HBbmIiDiMjH2rSNr8BGFNWpJxxzu0bNrK7JIcnoJcREQcwvoD7zNx41ia\n+13G6jve4armHcwuySnYNEZeWVlJYmIi+fn5eHl5MXv2bNq0aVNrnTVr1rBs2TI8PT0ZPnw4cXFx\nlJWVkZiYSGFhIQEBAaSkpBAaGsrevXt5+umnAejSpQszZsy45MZERMR5ZB/ZzB/X34eflx9v3p7B\ntS2uM7skp2HTGfnatWsJCgpi5cqVPPTQQ6SmptZ6v6ysjEWLFvHGG2+wfPlyli1bxvHjx1m9ejVt\n2rThzTffZOzYsaSlpQEwa9YskpKSWLVqFSUlJWzatOnSOxMREaew2/JvRq67l2qjmtcH/Y2IVpFm\nl+RUbArynJwcYmNjAYiKiiI3N7fW+3l5edxwww0EBgbi7+9Pjx49yM3N5cCBA4SHhwPQq1cvdu3a\nRUVFBUeOHKlZPmDAAHJyci6lJxERcRJfFu3n3n/dRWllCS/fspiBbW8xuySnY9NP64WFhYSEnLmK\n0NPTEw8PDyoqKvD19T3nfYCQkBAsFgudO3dm06ZN3HbbbWzfvp38/HyKiooICgqqWbdFixZYLJYL\nfn5wcBO8ve3/YPzQ0EC779PRqWf34I49g3v27Uw9HzxxkBHv3cUPp34g/TfpjOk5yqb9OFPPDaHO\nIM/IyCAjI6PWsry8vFqvDcO44D7Ovj9s2DD27dtHfHw8vXv3rhX29d0XQFFRWZ3rXKzQ0EC3e16v\nenYP7tgzuGffztRzYXkhd/7zNg4VH2JanxkMbTvCptqdqedLdb4vLHUGeVxcHHFxcbWWJSYmYrFY\n6Nq1K5WVlRiGUXM2DhAWFkZhYWHN62PHjnHjjTfi6+tbcyFbaWkpH330ESEhIRw/frxm3YKCAsLC\nwi6uOxERcRonK4oZsfZuvjr+JQ93f5SJPR4zuySnZtMYeXR0NJmZmQBkZWURGVn7woRu3bqxZ88e\niouLKS0tJTc3l169erFp0yYWLFgAnLmqPSYmBh8fHzp06MDOnTsB2LBhAzExMZfSk4iIOKjyqnIS\n1o04c4HbNffxVB/dpXSpbBojHzJkCNnZ2cTHx+Pr60tKSgoA6enpRERE0L17dyZPnsyYMWPw8PBg\n/PjxBAYGEhkZyYoVKxg+fDjNmzdn/vz5ACQlJTF9+nSsVivdunUjKirKfh2KiIhDqKyu5E8bRpOd\nv5k7Og7l+f4LNIOZHXgY9RmUdjANMR7iTuMsZ6ln9+COPYN79u3IPVsNKxM+eoiM/avof+UA/nb7\navy8/C55v47cs72db4xcT3YTEZEGZRgG0zZPIWP/Knq2jGDp4BV2CXE5Q0EuIiINat7OFBbvefWn\nmcwyaObTzOySXIqCXEREGszi3a/w/I7ZtA1qz9/v+KdmMmsACnIREWkQ/zuTWaumrc0uySUpyEVE\nxO40k1njUZCLiIhdZR/ZzB/Wj8LPy48VQzSTWUOz6T5yERGRX3J2JjOrYWXZ4JX0bq2ZzBqaglxE\nROzi5zOZvXbrG5rJrJEoyEVE5JIdPnmI4f8ayg+nfiD15jTuvPous0tyGxojFxGRS1JYXsjwfw3l\nSMlhpvWZQcK1o80uya0oyEVExGaaycx8CnIREbGJZjJzDApyERG5aJrJzHEoyEVE5KJYDSuPZI1j\n/YH36X/lAF665TW8PL3MLsttKchFRKTezs5k9tb+v2smMwehIBcRkXrTTGaOR0EuIiL18trulzWT\nmQNSkIuISJ1W71vJ1M1TNJOZA1KQi4jIBa0/8D6PbBynmcwclIJcRETOa8uRTzWTmYPTs9ZFROQX\n5R37jIR1IzSTmYNTkIuIyDm+LNrPiLV3U1pZQvqtSzWTmQNTkIuISC0/n8lsXv8X+e3Vd5tdklyA\nxshFRKSGpcxC3L9+WzOT2ajr7je7JKmDglxERIAzM5nFv3cPXx//ivE3PqKZzJyEglxERGrNZPb7\na0Yxve8zZpck9aQgFxFxc/87k9m8/i9qJjMnoiAXEXFjmsnM+dl01XplZSWJiYnk5+fj5eXF7Nmz\nadOmTa111qxZw7Jly/D09GT48OHExcVRVlZGYmIihYWFBAQEkJKSQmhoKAkJCZSVldGkSRMApkyZ\nwvXXX3/p3YmIyHlpJjPXYFOQr127lqCgIFJTU9m8eTOpqaksWLCg5v2ysjIWLVrEW2+9hY+PD8OG\nDSM2NpZ33nmHNm3akJaWxs6dO0lLS+PZZ58FYPbs2XTu3Nk+XYmISJ00k5lrsOmn9ZycHGJjYwGI\niooiNze31vt5eXnccMMNBAYG4u/vT48ePcjNzeXAgQOEh4cD0KtXL3bt2nWJ5YuIiC00k5nrsOmM\nvLCwkJCQMwfd09MTDw8PKioq8PX1Ped9gJCQECwWC507d2bTpk3cdtttbN++nfz8/Jp10tLSKCoq\nomPHjiQlJeHv73/ezw8OboK3t/3HcEJDA+2+T0ennt2DO/YM7tl3fXpenrecqZun0KpZKzbe9yEd\nQzo2QmUNxx2P88/VGeQZGRlkZGTUWpaXl1frtWEYF9zH2feHDRvGvn37iI+Pp3fv3jVhP2rUKLp0\n6ULbtm1JTk5mxYoVjBkz5rz7Kyoqq6vsixYaGojFctLu+3Vk6tk9uGPP4J5916fnzG/XcX/m/TT3\nu4yVQ94mqDrMqf89udNxPt8XljqDPC4ujri4uFrLEhMTsVgsdO3alcrKSgzDqDkbBwgLC6OwsLDm\n9bFjx7jxxhvx9fVlxowZAJSWlvLRRx8B1PxMDzBw4EDWrVt3Ea2JiEhdDMNg7TdrGPfhH2pmMrvu\ncl1U7ApsGiOPjo4mMzMTgKysLCIja8+I061bN/bs2UNxcTGlpaXk5ubSq1cvNm3aVHNR3Jo1a4iJ\nicEwDEaPHk1xcTEA27Zto1OnTpfSk4iI/Myugh0MfXcIY9YnYDWsvD7ob5rJzIXYNEY+ZMgQsrOz\niY+Px9fXl5SUFADS09OJiIige/fuTJ48mTFjxuDh4cH48eMJDAwkMjKSFStWMHz4cJo3b878+fPx\n8PBg+PDhjB49moCAAFq2bMmECRPs2qSIiDv65sTXPLf1GdZ8/U8Abms/mGl9ZtAlpKvJlYk9eRh1\nDXA7oIYYD3GncZaz1LN7cMeewT37PtuzpczC/F1zWPbF61RZq+gR1pPkqJn0vSLa7BLtzp2Os81j\n5CIi4hxKK0p5Yefz/OWzBZRUnqR90FVM6/M0d3QcqkeuujAFuYiIk6uyVrFq7wqe3/kcR0uO0sK/\nBVP7PE/Ctffj6+Vb9w7EqSnIRUSclGEYbPguk5k5yewr2kuAdwCP9Xych7s/SqBvkNnlSSNRkIuI\nOKFdBTt4Jmc6Oflb8PTwZOQ195EyaBa+pxXg7kZBLiLiRC50JXpokPtc+CX/pSAXEXECheWFzN85\nhze+WEKVtYruYT1I7juTqF/dZHZpYjIFuYiIAyurLOPVvEW6El3OS0EuIuKAqqxV/H3vm8zZMYvv\nS89ciZ4UOZdR1z2gK9GlFgW5iIgDMQyDD77L5FldiS71pCAXEXEQuQU7mZHzVK0r0f8c8SStm11h\ndmniwBTkIiIm+/bENzy39Rne/fpt4MyV6FP7PE3XkGtMrkycgYJcRMQkuhJd7EFBLiLSyHQlutiT\nglxEpJHoSnRpCApyEZEGpivRpSEpyEVEGlBuwU6eyZlOdv5mXYkuDUJBLiLSAP73SvRb2w1iWt8Z\nuhJd7E5BLiJiR2evRF/2xetUWit1Jbo0OAW5iIgdlFWWkb77JdJyX6i5En1qn2Tu7HiXrkSXBqUg\nFxG5BNXWalbtXaEr0cU0CnIRERsYhsGH363n2a3J7P3x/3QluphGQS4iUg+GYfBd8QG2Hs1ma342\n2fmbOVD8LZ4envz+mlE8EZGkK9HFFApyEZFfYDWs7C/aR07+Frbmb2Hr0RyOlubXvB/k25w7O97F\n4xGJuhJdTKUgFxHhzFPX9ljyyDmazdaj2WzLz6bodFHN+5cHhHJHx6H0bR1F5BVRXBtyHV6eXiZW\nLHKGglxE3FJ5VTmfFexi69FscvK3sLNgB6WVJTXvtw1sR2z7QfRpHUXfK6Lo0PxqXX0uDklBLiJu\n4WRFMTu+30ZO/pkz7s8KdlFhrah5v3NwF/q0jqbvFVH0aR3FrwKvNLFakfpTkIuIS7KUWlj79Qa2\nHc0m52g2nxfuxmpYAfD08OSGy7vR56fQjmzdl8sDLje5YhHbKMhFxCUcPnnop5/Js9l2NJv9Rftq\n3vP19CWiVSR9W0fT54ooIlr11i1i4jJsCvLKykoSExPJz8/Hy8uL2bNn06ZNm1rrnDhxgkmTJtG0\naVPS0tIuuN3evXt5+umnAejSpQszZsy4tK5ExKUZhsHXx78i5+gWtv70U/mhkwdr3m/i3ZRbO95K\nzxaR9Lkiiu5hPfH39jexYpGGY1OQr127lqCgIFJTU9m8eTOpqaksWLCg1jrJycn07NmTvXv31rnd\nrFmzSEpKIjw8nMmTJ7Np0yb69+9/aZ2JiMuotlbznx8+rznj3no0m8JyS837wX7BDLrqdvr+NMZ9\n/eXhtG4ZjMVy0sSqRRqHTUGek5PD0KFDAYiKiiIpKemcdWbOnMkXX3xRK8h/abuKigqOHDlCeHg4\nAAMGDCAnJ0dBLuLGKqor+Pexz9j60xn3tu+3crKiuOb91k2v4O5Ow4hsHUXfK6LpHNwFTw9PEysW\nMY9NQV5YWEhISAgAnp6eeHh4UFFRga/vf58r3KxZs3ptV1hYSFDQf8eqWrRogcViOWfbnwsOboK3\nt/3v3wwNDbT7Ph2denYPjt7zqapTbD64mU+/+5RPDn7C1sNbOVV1qub9TiGdiGs7jH7t+tGvXT/a\nX9a+XreCOXrfDUE9u586gzwjI4OMjIxay/Ly8mq9NgzDpg//pe3qs6+iojKbPu9CQkMD3e5nOPXs\nHhy95w+/W8+fNz3GkZLDAHjgwTUtrqu5DaxP6yhaNm313w2qoLCw5Dx7+y9H77shqGfXdr4vLHUG\neVxcHHFxcbWWJSYmYrFY6Nq1K5WVlRiGUets/HzCwsLO2S40NJTjx4/XrFNQUEBYWFid+xIR5/ZD\n+Q9M2zyFf3y5Gm9Pbx64/o8MbHsLvVv14TL/YLPLE3EaNg0qRUdHk5mZCUBWVhaRkZE2b+fj40OH\nDh3YuXMnABs2bCAmJsaWskTECRiGwT+/fIubVvbiH1+u5sbQ7nww7BNS+qVya/vBCnGRi2TTGPmQ\nIUPIzs4mPj4eX19fUlJSAEhPTyciIoLw8HBGjx5NcXExBQUFJCQkMG7cuPNul5SUxPTp07FarXTr\n1o2oqCj7dSgiDiO/5AhTPpnE+gPvE+AdwNNRs/hT+Fi8PfVICxFbeRi2DnCbqCHGQ9xpnOUs9ewe\nHKFnq2Hlb/9ZxoycpzhZUUz0FTGkDkijQ/OODfaZjtB3Y1PPrs3mMXIRkUvxzYmvmZw1kS35nxLo\nG0TqzWmMvOY+TUAiYicKchFpEFXWKl7JW8Tc7bM4VX2KQe2HMKfffFo3u8Ls0kRcioJcROzu88I9\nPJb1MHmWz7g84HL+EvMKd3a8S2fhIg1AQS4idnO6+jQv7JxL2mcvUGWtIq7zCJ69aTYh/i3MLk3E\nZSnIRcQuth/dxqSPH2Z/0T6ubNaGeTcvYGDbWLPLEnF5CnIRuSQllSU8t3UGS/akY2Aw5oY/MTUy\nmWa+7v3YTJHGoiAXEZttPPghf970KIdOHuTqyzoxf8BC+rTua3ZZIm5FQS4iF63o1I9M35LE3/e9\niZeHF4/2eJxJvZ7QnN8iJlCQi0i9GYbB2m/eZconkykstxAeeiMvDFjIDZeHm12aiNtSkItIvRSU\nfs+UTyaz7tt/4e/lz1N9n2Fst4f1eFURk+lPoIhckGEYrNz7N6ZvSaK44gR9r4hm/s1pdLysk9ml\niQgKchG5gAMnvmXypkf49PDHNPMJZG6/Fxh13f14etg0caKINAAFuYico9pazWt7XiZl20zKqsqI\nbXcbc/u9wK8CrzS7NBH5HwpyEanl/374D5M+fphdBTsJ8Q8h9eY07u4Up8erijgoBbmIAFBRXcGL\nuaks2DWPSmsld3eKY+ZNc7g84HKzSxORC1CQiwi7CnbwWNbD7P3x/2jd9Aqe7/8Ct7YfbHZZIlIP\nCnIRN1ZaWUrK9pmk572EgcF9141het8ZBPoGmV2aiNSTglzETX1y+GMmfTyRg8UH6NC8I/Nv/gtR\nv7rJ7LJE5CIpyEXczInTx3k6exor/u+veHl4MaH7YzwekUiAd4DZpYmIDRTkIm5k3TdrmfLJJArK\nvue6FjewYMBCuoV1N7ssEbkECnIRN3Cs7BhJn/6ZNV//E19PX5IipzP+xkfw8fIxuzQRuUQKchEX\nZhgGy/69jEczH+X46eP0btWHFwYspFNwZ7NLExE7UZCLuKiDxd/x+KZH+PjQRpr6NGN2zDzuv/4P\neryqiItRkIu4mGprNUs/f42ZW2dQVlXKoKsHMavvPNoEtjW7NBFpAApyERdyuvo0I98bzqbDWQT7\nBTO3/3zGRf+RwsISs0sTkQaiIBdxEYZh8OjG8Ww6nMWv28by4sCXCWsSpmeki7g4BbmIi3h+x2z+\n8eVqerXszeuD/qb7wkXchK56EXEBf9/7JvN2ptA2qD1/HbJKIS7iRmw6I6+srCQxMZH8/Hy8vLyY\nPXs2bdq0qbXOiRMnmDRpEk2bNiUtLe2C2yUkJFBWVkaTJk0AmDJlCtdff/0ltibiHrKPbGbSxxNo\n7ncZbw7J0GxlIm7GpjPytWvXEhQUxMqVK3nooYdITU09Z53k5GR69uxZ7+1mz57N8uXLWb58uUJc\npJ6+KvqS0Zm/w8Bg6aC/0Tmki9kliUgjsynIc3JyiI2NBSAqKorc3Nxz1pk5c+Y5QV6f7USkfn4o\n/4HfvTeM46ePM//mv3DTr/qZXZKImMCmn9YLCwsJCQkBwNPTEw8PDyoqKvD19a1Zp1mzZvXeDiAt\nLY2ioiI6duxIUlIS/v7+5/384OAmeHt72VL6BYWGBtp9n45OPTunU1WnuOtfIzlQ/C3TYqYxIeah\nC67vCj3bwh37Vs/up84gz8jIICMjo9ayvLy8Wq8Nw7Dpw89uN2rUKLp06ULbtm1JTk5mxYoVjBkz\n5rzbFRWV2fR5FxIaGojFctLu+3Vk6tk5WQ0rYz8Yw5ZDW7jr6nuYcP2fL9iTK/RsC3fsWz27tvN9\nYakzyOPi4oiLi6u1LDExEYvFQteuXamsrMQwjFpn4+cTFhb2i9ud/bkdYODAgaxbt67OfYm4q7nb\nZ/HPr/5BRKtIXhz4su4TF3FzNo2RR0dHk5mZCUBWVhaRkZE2b2cYBqNHj6a4uBiAbdu20alTJ1vK\nEnF5q/auYP6u52kfdBXLBq/E3/v8Q1Ai4h5sGiMfMmQI2dnZxMfH4+vrS0pKCgDp6elEREQQHh5e\nE84FBQUkJCQwbty4X9zOw8OD4cOHM3r0aAICAmjZsiUTJkywa5MirmDzkU+Y/PFELvO7jDdvf0u3\nmYkIAB6GrQPcJmqI8RB3Gmc5Sz07jy+L9jPk7Vsoqywl4453ifrVTfXe1ll7vlTu2Ld6dm02j5GL\niLkKywuJf28YJ04f5y8DX7moEBcR16dHtIo4sFNVpxi1bgQHiw8wudcU7u36O7NLEhEHoyAXcVBW\nw8rEjQ+xs2A7d3eK44mIJLNLEhEHpCAXcVAp22byzldvE9m6Ly8OfEm3mYnIL1KQizigN/9vOQty\n59GheUeWDX4TPy8/s0sSEQelIBdxMJ8c/pjHNz1CsF8wb96eQYh/C7NLEhEHpiAXcSD7ftzLA5kJ\neOLJssEr6XDZ1WaXJCIOTrefiTiIY2XH+P17cRRXnOClW16jzxVRZpckIk5AZ+QiDqC8qpz73h/B\nwZPf8UREEsM632t2SSLiJBTkIiazGlYe/uhBdhXsJK7zCCb3mmJ2SSLiRBTkIiabtXUG//r6Hfpe\nEc38AX/RbWYiclEU5CImWv6fN/jLZy/Q8bKreWPQCt1mJiIXTUEuYpKPD23kiU2PEeIfworbMwj2\nDzG7JBFxQgpyERPs/fH/GLN+FF4eXiwbvIoOzTuaXZKIOCndfibSyArKCvj9e3GcrCjmldglRLbu\nY3ZJIuLEdEYu0ojKKssYte5eDp08SGLvadzdKc7skkTEySnIRRqJ1bAy/qM/8dmxXO7t8jse6/ln\ns0sSERegIBdpJM/mJPPeN2uIviKG1JvTdJuZiNiFglykESz74nUW/ftFrr6sE0sH/Q1fL1+zSxIR\nF6EgF2lgGw9+SOInk2nh34IA9XKeAAAZiUlEQVQ3b3+Ly/yDzS5JRFyIglykAf3nhy/4w/r78Pb0\nZtngVbRvfpXZJYmIi9HtZyINpKD0e0a+N5ySypOkxy6ld+tIs0sSERekM3KRBlBaWUrCuns5XHKI\nqZHJDO10j9kliYiLUpCL2Fm1tZqxH/6Bf1s+43ddE5jYY5LZJYmIC1OQi9jZjJynyPz2PWJ+1Z/n\n+y/QbWYi0qAU5CJ2tPTzxbySt5DOwV14fdByfLx8zC5JRFycglzETj76bgNPfvo4lwdczorbM2ju\nd5nZJYmIG1CQi9jB54V7+MOG0fh6+vLXwatoF9Te7JJExE3YFOSVlZVMnjyZ+Ph4Ro4cyaFDh85Z\n58SJE4wZM4aJEyfWWr59+3b69u1LVlZWzbK9e/cyYsQIRowYQXJysi0liZjm+9KjjHxvOKWVJSy6\nJZ1erXqbXZKIuBGbgnzt2rUEBQWxcuVKHnroIVJTU89ZJzk5mZ49e9ZadvDgQZYuXUqPHj1qLZ81\naxZJSUmsWrWKkpISNm3aZEtZIo2upLKE3783nPzSI0zrM4M7Og41uyQRcTM2BXlOTg6xsbEAREVF\nkZube846M2fOPCfIQ0NDWbhwIYGBgTXLKioqOHLkCOHh4QAMGDCAnJwcW8oSaVTV1mrGfjCGPYV5\njLzmPiZ0f9TskkTEDdn0ZLfCwkJCQkIA8PT0xMPDg4qKCnx9/zsRRLNmzc7ZLiAg4JxlRUVFBAUF\n1bxu0aIFFovlgp8fHNwEb28vW0q/oNDQwLpXcjHq2XaPZT7G+gPvc0uHW3j9ntcc+gp1dzzO4J59\nq2f3U2eQZ2RkkJGRUWtZXl5erdeGYditoPrsq6iozG6fd1ZoaCAWy0m779eRqWfbLdnzKgu2LaBL\ncFdeGbCU4z+eAk5deoENwB2PM7hn3+rZtZ3vC0udQR4XF0dcXFytZYmJiVgsFrp27UplZSWGYdQ6\nG78YISEhHD9+vOZ1QUEBYWFhNu1LpDF8cCCTqZunEBoQxorbMwjya252SSLixmwaI4+OjiYzMxOA\nrKwsIiNtnwzCx8eHDh06sHPnTgA2bNhATEyMzfsTaUh7Cnfzxw334+flx/Ihq2gb1M7skkTEzdk0\nRj5kyBCys7OJj4/H19eXlJQUANLT04mIiCA8PJzRo0dTXFxMQUEBCQkJjBs3jtOnT7NkyRK++eYb\nvvjiC5YvX87rr79OUlIS06dPx2q10q1bN6KiouzapIg9HC3J5/fvxVFeVcbi2/5Kj5a9zC5JRAQP\nw54D3I2kIcZD3Gmc5Sz1XH8llSXc+c9BfF64m+S+MxnffWLdGzkIdzzO4J59q2fXdr4xcj3ZTaQO\n1dZqHtxwP58X7mbUtQ8w7sYJZpckIlLDpp/WRS5W9pHNPL7pEb4v/R5/b38CvAPw9/LH3zsAPy+/\nM6+9z7w+uzzA2x9/rzPL/bz9Cfhpuf9PywO8a7/29/b76e8BNZ/h6XHp31Wf2pLIB9+tZ0CbX5PS\nb55mMxMRh6IglwZVZa0ideccXtj1PB540CXkGk5Xn+JU1SmKTv9IeekpTlWVU21UN8jn+3r6/jfs\nvQNo6huAj4ffL35Z+O+XAv+aLwf5JYdZvOdVrgm5lsW3LcPbU39kRMSx6P9K0mAOnTzI2A/+wPbv\nt9ImsC2vxC4hotUv3+FQWV3JqepyyqvOBPupqlOcqi7nVNXpn/5+Zll5VTmnqv+7Tnl1Oadr1vnp\n/Zptf1qv+nTN+sdKT1JeWU55VTkG9bs8JKxJS1bcnkGgb1DdK4uINDIFuTSINV/9k0kfT6S44gRD\nr76b5/svuOC0nj5ePvh4+TR4WJ69MMYwDCqsFT/70nCqJvjLf/ZF4XT1KfpcEU3LJi0btC4REVsp\nyMWuSitLmb7lSZb/5w2aeDdhwYBFxHcd6XDjyh4eHvh5+eHn5UdzP7OrERGxnYJc7Obzwj08uOF+\nvjy+n+svDyc9dilXB3cyuywREZem28/kkhmGweLdrzDorQF8eXw/D4aP4/17PlKIi4g0Ap2RyyX5\nofwHHtk4lg3fZdLCvwVpA18mtv0gs8sSEXEbCnKx2aeHNzHuwz9SUPY9/a4cwKJfv0rLpq3MLktE\nxK0oyOWiVVZXMnfHc6TlzsfL04un+j7D+Bsn2uXhKyIicnEU5HJRDpz4lrEfjmFXwU7aBbXn1djX\nNXmIiIiJFORSb29/mcHjHz9KSeVJ7uk0nLn95+shKSIiJlOQS51KKktI+vTPrNq7gqY+zVj461cZ\n3iXe7LJERAQFudRht+Xf/GnD/Xxz4mu6hXbn1dgldLjsarPLEhGRn+jqJPlFVsPKy/9eyOB//Jpv\nTnzNuBsn8t7dHyjERUQcjM7I5RzHyo4xceNDbDz4IaEBYfzl168wsO0tZpclIiK/QEEutWQd/IiH\nP3oQS/kxBra9hbSBrxDWJMzsskRE5DwU5AJARXUFz217hpf+nYaPpw8zop7jwW7jdG+4iIiDU5AL\n3xz/igc/GEOe5TM6NO9I+q1LCQ+90eyyRESkHhTkbu7ve99kyieTKasqZUTX3/NczPM082lmdlki\nIlJPCnI3dbKimMfeHsuKPSto5hPIy7cs5p7Ow80uS0RELpKC3A3lFuzkwQ8e4LviA/Rs2YuXb1lC\n++ZXmV2WiIjYQEHuRqyGlYWfvUjK9meptlbz5E1P8vB1j+Pj5WN2aSIiYiMFuZsoKP2e8R89yCeH\ns2jZpBUv3fIad3f/DRbLSbNLExGRS6AgdwMffreeCR89xA+nfuDWdoN4ceDLtAhoYXZZIiJiBwpy\nF3a6+jTP5kwnfffL+Hr68txNcxlzw4N4eHiYXZqIiNiJgtxFfVm0nwc/eIDPC3fT6bLOvHrrUq6/\n/AazyxIRETuz6bFdlZWVTJ48mfj4eEaOHMmhQ4fOWefEiROMGTOGiRMn1lq+fft2+vbtS1ZWVs2y\nhIQE7rnnHhISEkhISODzzz+3pSwBDMNgxX/+SmxGPz4v3E3CtaPZELdJIS4i4qJsOiNfu3YtQUFB\npKamsnnzZlJTU1mwYEGtdZKTk+nZsyd79+6tWXbw4EGWLl1Kjx49ztnn7Nmz6dy5sy3lyE9OnD7O\n4x8/yrtfv01zv8tY8utXuKPjULPLEhGRBmTTGXlOTg6xsbEAREVFkZube846M2fOpGfPnrWWhYaG\nsnDhQgIDA235WLmA7Ue3MXD1Tbz79dv0btWHjcM3K8RFRNyATWfkhYWFhISEAODp6YmHhwcVFRX4\n+vrWrNOs2bmP+QwICDjvPtPS0igqKqJjx44kJSXh7+9/3nWDg5vg7e1lS+kXFBrqfF8wqq3VpGxO\nIfnjZAwMpvebzlP9n8Lbs36H1hl7vlTq2X24Y9/q2f3U+X/7jIwMMjIyai3Ly8ur9dowjEsqYtSo\nUXTp0oW2bduSnJzMihUrGDNmzHnXLyoqu6TP+yWhoYFOd091fskRxn/4J7bkf8oVTX/FS7e8RtSv\nbqLoh/J6be+MPV8q9ew+3LFv9ezazveFpc4gj4uLIy4urtayxMRELBYLXbt2pbKyEsMwap2NX6yz\nP9MDDBw4kHXr1tm8L3fx/rfv8ejGcRSdLmLIVXfwwoC/EOwfYnZZIiLSyGwaI4+OjiYzMxOArKws\nIiMjbS7AMAxGjx5NcXExANu2baNTp042788drNq7gvvej6e8qpy5/V5g6aC/KcRFRNyUTWPkQ4YM\nITs7m/j4eHx9fUlJSQEgPT2diIgIwsPDa8K5oKCAhIQExo0bx+nTp1myZAnffPMNX3zxBcuXL+f1\n119n+PDhjB49moCAAFq2bMmECRPs2qQrWffNWh7NGk+wXzBv/fZf3HB5uNkliYiIiTyMSx3gNkFD\njIc4wzjLp4c3Eb/2Hrw9ffjHb9fQs2XEJe3PGXq2N/XsPtyxb/Xs2s43Rm7TT+vS+D4r2MWo9+MB\nWDb4zUsOcRERcQ16RKsT2P/jPuLfu4fyqjIW3/pX+rcZYHZJIiLiIBTkDu7QyYPE/eu3/HjqRxYM\nWMRvOt5pdkkiIuJA9NO6AztWdoy4Nb/laGk+yX1n8rtrEswuSUREHIyC3EEVnz7BiLV3882Jr3mk\nx2TGd59Y90YiIuJ2FOQOqKyyjJHr7uXzwt2MuvYBkiKnm12SiIg4KAW5g6msruQP60ex9Wg2Q6++\nmzn9UvHw8DC7LBERcVAKcgdiNaxM2PgQHx7cwMC2t7Dw1+l4edp/chgREXEdCnIHYRgGSZ/+mbe/\nzCCiVSRLbluOr5ftz68XERH3oCB3EHN2zOL1z1/jmpDrWDFkNU19mppdkoiIOAEFuQN4NW8R83fO\npX3QVay+459c5h9sdkkiIuIkFOQmW7V3BU9teZKWTVqRcee7tGzayuySRETEiSjITfT+t+/xWNbD\nXOZ3GavveId2Qe3NLklERJyMgtwkm498wp82jMbPy583b3+La1pca3ZJIiLihPSsdRP8+1guCetG\nYDWsLB+ygl6teptdkoiIOCkFeSPb/+M+Rqy9m/KqMl679Q1ubjPQ7JJERMSJKcgb0aGTBxn+r6H8\neOpH5t/8F+7oONTskkRExMlpjLyRWMosxK35LfmlR5je91lGXnuf2SWJiIgLUJA3guLTJ7h37V18\nc+JrJnafxMPdHzG7JBERcREK8gZWXlVeM5NZwrX3M7VPstkliYiIC1GQN6Cfz2R2Z8e7mNtvvmYy\nExERu1KQNxCrYWXixrF88N16bm4zkJdueU0zmYmIiN0pyBuAYRhM3fwE//hyNb1a9mbpoBWayUxE\nRBqEgrwBzN3xHEv2pHNNyHW8eXuGZjITEZEGoyC3s/S8l0jdOYd2Qe01k5mIiDQ4Bbkd/X3vm0zb\nknhmJrM7NJOZiIg0PAW5nWR+u45Hs8bXzGTWvvlVZpckIiJuQEFuB1uOfMofN9yHn5cfK27P0Exm\nIiLSaGx61nplZSWJiYnk5+fj5eXF7NmzadOmTa11Tpw4waRJk2jatClpaWkAVFVVMXXqVA4ePEh1\ndTVPPPEEvXr1Yu/evTz99NMAdOnShRkzZlxaV43o5zOZ/XXwKiJaRZpdkoiIuBGbzsjXrl1LUFAQ\nK1eu5KGHHiI1NfWcdZKTk+nZs2etZe+++y4BAQGsXLmSWbNmkZKSAsCsWbNISkpi1apVlJSUsGnT\nJlvKanRfFu0nfu09lFaW8PItixnQ9tdmlyQiIm7GpiDPyckhNjYWgKioKHJzc89ZZ+bMmecE+Z13\n3smTTz4JQEhICMePH6eiooIjR44QHh4OwIABA8jJybGlrEZ1+OQh4tb8lh9O/cC8m1/kzqvvMrsk\nERFxQzb9tF5YWEhISAgAnp6eeHh4UFFRga/vfx960qxZs3O28/HxqfnnZcuW8Zvf/IaioiKCgoJq\nlrdo0QKLxXLBzw8OboK3t/2fkhYaGliv9Y6VHmPE3+8iv/QIc26Zw6ToCXavpbHUt2dXop7dhzv2\nrZ7dT51BnpGRQUZGRq1leXl5tV4bhnFRH7pixQq++OILXnnlFX788ceL3ldRUdlFfV59hIYGYrGc\nrHO94tMnuOvd37D/h/083P1R7u88tl7bOaL69uxK1LP7cMe+1bNrO98XljqDPC4ujri4uFrLEhMT\nsVgsdO3alcrKSgzDqHU2fiEZGRls3LiRl156CR8fn5qf2M8qKCggLCysXvtqbOVV5SS8P4I9hXmM\nvOY+nurjPBfliYiIa7JpjDw6OprMzEwAsrKyiIys35Xahw4dYtWqVSxcuBA/Pz/gzM/tHTp0YOfO\nnQBs2LCBmJgYW8pqUJXVlfxx/X3k5G/hzo538Xz/BZrJTERETGfTGPmQIUPIzs4mPj4eX1/fmqvP\n09PTiYiIIDw8nNGjR1NcXExBQQEJCQmMGzeOnJwcjh8/zp/+9KeafS1ZsoSkpCSmT5+O1WqlW7du\nREVF2ac7O7EaVh7JGseG7zLpf+UAFt2SrpnMRETEIXgYFzvA7QAaYjzkfOMsZ2cyW7znVXq2jCDj\nzndp5nPuhXzOyJ3Gls5Sz+7DHftWz67tfGPkerJbHZ7fMZvFe17lmpBrefP2DJcJcRERcQ0K8gt4\nbffLzNuZQtug9vz9jn8S7B9idkkiIiK1KMjPY/W+lUzdPIWwJi3JuOMdWjVtbXZJIiIi51CQ/4LM\nb9fxyMZxNP9pJrOrmncwuyQREZFfpCD/H7VmMhuSwbUtrjO7JBERkfOy6fYzV5V37LOamcyWDV5J\n79aayUxERBybgvwnewv3MmLt3ZRWlpB+61IGtr3F7JJERETqpCDnzExmv3130JmZzPq/yG+vvtvs\nkkREROrF7cfIyyrLGP6voRwqPsS0Pk8z6rr7zS5JRESk3tz+jNxSfowjJYd58qYnmXDDY2aXIyIi\nclHcPsjbBbXnqzGHuaJViNs85k9ERFyH2/+0DuDj5WN2CSIiIjZRkIuIiDgxBbmIiIgTU5CLiIg4\nMQW5iIiIE1OQi4iIODEFuYiIiBNTkIuIiDgxBbmIiIgTU5CLiIg4MQW5iIiIE1OQi4iIODEPwzAM\ns4sQERER2+iMXERExIkpyEVERJyYglxERMSJKchFREScmIJcRETEiSnIRUREnJi32QU0tMrKShIT\nE8nPz8fLy4vZs2fTpk2bWuucOHGCSZMm0bRpU9LS0i643d69e3n66acB6NKlCzNmzGjslupUn57X\nrFnDsmXL8PT0ZPjw4cTFxVFWVkZiYiKFhYUEBASQkpJCaGgoCQkJlJWV0aRJEwCmTJnC9ddfb0Zr\n52Xvnl35OBcUFJCUlERFRQVWq5Unn3yS66+/noEDB9KqVSu8vLwAmDdvHi1btjSjtQuyd9/Z2dnM\nnz8fLy8v+vXrx/jx403q7Pxs7fnll18mOzsbAKvVSmFhIevXr3eKY23vnp3hONvMcHFvv/228fTT\nTxuGYRiffvqp8cgjj5yzziOPPGIsWrTImDBhQp3bjRw50sjLyzMMwzAmTZpkfPzxxw3dwkWrq+fS\n0lLj1ltvNYqLi43y8nLj9ttvN4qKioylS5cac+fONQzDMHbs2GFMmzbNMIwzPe/bt69xm7hIDdGz\nqx7nlJQUY+XKlYZhGMauXbuMBx54wDAMwxgwYIBRUlLSuE3YwN59Dx482MjPzzeqq6uN+Ph448sv\nv2zchurB1p7/dx+vvfaaYRjOcazt3bMzHGdbufxP6zk5OcTGxgIQFRVFbm7uOevMnDmTnj171rld\nRUUFR44cITw8HIABAwaQk5PTwB1cvLp6zsvL44YbbiAwMBB/f3969OhBbm4uBw4cqOmtV69e7Nq1\nq9Frt5U9e3b14xwcHMzx48cBKC4uJjg4uNFrvxT27PvQoUM0b96c1q1b4+npSf/+/V3qWJ9VVVXF\nypUrGTlyZKPWfSns2bOzHGdbufxP64WFhYSEhADg6emJh4cHFRUV+Pr61qzTrFmzem1XWFhIUFBQ\nzTotWrTAYrE0cAcXr66ef/4+QEhICBaLhc6dO7Np0yZuu+02tm/fTn5+fs06aWlpFBUV0bFjR5KS\nkvD392/cpupgz56Liopc+jiPHj2aYcOG8c4771BSUsLKlStr1klOTubIkSP07NmTyZMn4+Hh0bhN\n1YM9+7ZYLOese+jQocZtqB5s7fmsDRs2cNNNN9X6c+vox9qePTvLcbaVSwV5RkYGGRkZtZbl5eXV\nem3Y+ETaX9rO1n3Zkz16Pvv+sGHD2LdvH/Hx8fTu3bvmP/xRo0bRpUsX2rZtS3JyMitWrGDMmDF2\n7OLiNEbPF7OvxmDPnhcvXszgwYMZO3YsWVlZzJkzh4ULFzJx4kRiYmJo3rw548ePZ/369QwaNMi+\njVykhu77gQcesG/BdmDPns/6xz/+Ues6D0c71o3RsytzqSCPi4sjLi6u1rLExEQsFgtdu3alsrIS\nwzBqnY2fT1hY2DnbhYaG1vw0B1BQUEBYWJjd+7gYtvQcFhZGYWFhzetjx45x44034uvrW/Mffmlp\nKR999BFAzc9bAAMHDmTdunUN2VKdGrrnkJAQlz7OH3zwAY8++igA0dHRNf0PHTq0Zt1+/fqxf/9+\n04O8ofv+33Vd7VgDlJWV8f3333PllVfWvO9ox7qhe3bE42xPLj9GHh0dTWZmJgBZWVlERkbavJ2P\njw8dOnRg586dwJmfbmJiYhqm8EtQV8/dunVjz549FBcXU1paSm5uLr169WLTpk0sWLAAOHM1aExM\nDIZhMHr0aIqLiwHYtm0bnTp1atyG6sGePbv6cW7Xrl3N2c7u3btp164dJ0+eZMyYMVRUVACwY8cO\nhzzOYN++r7zySkpKSjh8+DBVVVVkZWURHR3d6D3VxdaeAfbu3UuHDh1q1nWWY23Pnp3lONvK5Wc/\nq66uZtq0aRw4cABfX19SUlJo3bo16enpREREEB4eXhNUBQUFdOrUiXHjxtG7d+9f3O6rr75i+vTp\nWK1WunXrxpNPPml2i+eoq+fu3buTmZnJkiVL8PDwYOTIkdx5552cOnWKiRMncvz4cZo3b878+fMJ\nDAxk3bp1LF68mICAAFq2bMmsWbMICAgwu81a7N2zKx/nY8eOMXXqVE6dOgXA1KlT6dq1K8uWLeOd\nd97Bz8+Pa6+9lqeeesrhxk3B/n3v2LGDefPmAXDrrbeaOmx0Prb2DNTcevXzn5md4Vjbu2dnOM62\ncvkgFxERcWUu/9O6iIiIK1OQi4iIODEFuYiIiBNTkIuIiDgxBbmIiIgTU5CLiIg4MQW5iIiIE1OQ\ni4iIOLH/B6VGBvEpEpBfAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jrsUps0nu8vj",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "** Question **
\n",
+ "Why did I created a session to plot the graph?
\n",
+ "[Ans]"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "P3-iuxE4sjAf",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the placeholders\n",
+ "\n",
+ "# Placeholders?\n",
+ "# The input to the model changes on iteration\n",
+ "# So we cannot have a constant in the input as we did before\n",
+ "# And thus we need placeholders which we can change on each \n",
+ "# iteration of the training\n",
+ "\n",
+ "x = tf.placeholder(tf.float32, name='x')\n",
+ "y = tf.placeholder(tf.float32, name='y')"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "8hPRkaoxvRyV",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the linear regression model\n",
+ "\n",
+ "# tf.Variable?\n",
+ "# We define the model parameters as tf.Variables\n",
+ "# as they get updated throghout the training.\n",
+ "# And variables denotes something which changes overtime.\n",
+ "\n",
+ "W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ "b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ "\n",
+ "pred_y = (W*x) + b"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "cSw1P8bkv96r",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the loss function\n",
+ "# We are going to use the mean squared loss\n",
+ "loss = tf.reduce_mean(tf.square(y - pred_y))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "5G4uQqjsygNj",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the optimizer\n",
+ "# And specify the which value (i.e. loss) it has to minimize\n",
+ "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "ttI7ZT-ozAm1",
+ "colab_type": "code",
+ "outputId": "6608e6a9-6834-4368-f520-9bc807f083ca",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 439
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# So the graph is now built\n",
+ "# Now let's execute the graph using session\n",
+ "# i.e. lets train the model\n",
+ "\n",
+ "# What it is to train a model?\n",
+ "# To update the paramters in the graph (i.e. tf.Variables)\n",
+ "# So that the loss is minimized\n",
+ "\n",
+ "# Okay let's start!\n",
+ "with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 20,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.0023985624\n",
+ "Loss after epoch 20 is 0.0023969896\n",
+ "Loss after epoch 40 is 0.0023954175\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 4.024094e-05\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAe0AAAFKCAYAAAAwrQetAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3Xd8U3Xbx/HPSdKVpqWDFqEsrewh\nS2QIshURQW5FZD3IkqnIKpRRoNBFKYogssQBSGUpLkC8QRCwTEEqG9lQ2tKWJulKcp4/uK0ilBbo\nDNfbly8yzvnlukjpN+fknPNTVFVVEUIIIUSxpynqAoQQQgiRNxLaQgghRAkhoS2EEEKUEBLaQggh\nRAkhoS2EEEKUEBLaQgghRAmhK+oC7iU+PrWoS8DTU09Skrmoyygw0l/JZu/9gf33KP2VfPndo4+P\nW47PyZZ2LnQ6bVGXUKCkv5LN3vsD++9R+iv5CrNHCW0hhBCihJDQFkIIIUoICW0hhBCihJDQFkII\nIUoICW0hhBCihJDQFkIIIUoICW0hhBCihCjWF1cpjj74YC4nThzjxo1E0tPTKVfOD3f3UoSEzM6X\n8V99tTO+vmXQaP7+PDV//uKHHveXX37mmWeacfNmCsuWLWL8+EkPPaYQQojClafQPnnyJMOGDaNf\nv3707t37tud2795NVFQUWq2Wli1bMnz4cABCQkI4fPgwiqIQGBhI3bp1uXr1KuPHj8dqteLj48Ps\n2bNxdHTM/64K0MiR7wLw/fffcPbsGUaMGJXvrxEZOQ+9Xp+vY65evZIGDZ7G27u0BLYQQpRQuYa2\n2WwmODiYpk2b3vX5mTNnsmzZMsqUKUPv3r15/vnnuXHjBufPnyc6OpozZ84QGBhIdHQ08+bNo2fP\nnnTs2JGoqCjWrl1Lz549872ponDw4H5Wr16B2WxmxIh3GTNmBN999xMAkyePp1u37lSvXoOQkOmk\npqZitVoZNWocTz5ZJU/jd+rU9o7xDh06gMlk5MKF81y+fIm33x5D06bN2bTpO9aujUZRFHr06EVW\nVhZ//HGUsWPfZsKEKUyfPpllyz7n4MH9LF++CFVV8PHxZeLEqWzdupkjR34jOTmJCxfO07NnH156\nqWuB/b0JIYTIu1xD29HRkSVLlrBkyZI7nrt48SKlSpWibNmyADz33HPs2bOHGzdu0K5dOwD8/f1J\nSUnBaDQSExPD9OnTAWjdujUff/zxQ4X2tN2T+ebMVw+8/t109u/KtGYzH2jdM2dO88UX63Pce/Dl\nl1/wzDPN6Ny5K3/+eZb334/kvfc+fJhyuX49jsjIefz6626+/nodTz1Vj08+Wcqnn35BZmYWs2YF\nERYWxdKlHxEZOY+UlOTsdSMjQ/nss0/R6QxERYXz44+bUBSFM2dO89FHH3Pp0kWCggIltIUQ4i5u\npCey+c8f6F+qT6G9Zq6hrdPp0Onuvlh8fDxeXl7Z9728vLh48SJJSUnUqlXrtsfj4+NJS0vLDjRv\nb2/i4+Pv+dqenvp7XtNV7+KIRqPk1sJ90bs43nGx9rtdvN3NzRm9/u9lPTz01KxZAz8/bwAURcl+\nzsnJAQ8PPSdOxHLjxg22bdsCQEZG2h1ja7UaJk58F632Vt+enp7MmzfvruO5ujrRtOkz+Pi4Ua3a\n42RkpJGScp0qVZ6kfHkfAJYtW5I9bunSBrTaLHQ6DQ4OVnQ6bfYHrlatWrBv3z5q1qzJ00835LHH\nPHBzcyAtzXTPi9eXBCW9/tzYe39g/z1KfyVLhiWDBfsWELwjmOT0ZMqV9uHVmq8WymsXyoFoqqrm\n6bF/y23WlPH1pzK+/tQHrisn/5xdzMfH7a6zjaWmpmM2Z2Y/l5xsRlWV7PuqqmbfNpnSsp8fOXIM\ntWvXvetrAVitNkJD5972nXZ8fOpdxzOZMnBwcCE+PpWkJBOZmRZSUtJJT8+867gJCUZSUkxYLDYS\nE01YLNbs8RMTb5KebiE1NZ3MTBvx8amYzWasVluxmG3tQeX0/tkLe+8P7L9H6a/kUFWVb89+zYw9\nUzl/8xylnDyY3iyEV6q/kq89FtgsX76+viQkJGTfj4uLw9fX947Hr1+/jo+PD3q9nvT09NuWtVeK\nopCenk56ejonT54AoGbN2uzYsR2AP/88y+rVKx5qvLupVKkyFy6cx2w2k5GRwahRw1BVFUXRYLVa\ns5dzd3dHURSuXLkCwG+/HaR69RoP0KkQQti/A3H76LzheQZs7stl4yUG1x1KTK9DDK03Aq2mhMzy\nVb58eYxGI5cuXcJisbBt2zaaN29O8+bN2bx5MwCxsbH4+vpiMBho1qxZ9uNbtmyhRYsWD99BMdW1\n66sMHvx/hIRMp1q1W2H46quvc/nyRYYNG0h4+Ezq1WvwUOPdjYuLCwMGDGHUqGGMHPkWnTt3RVEU\n6tdvwLBhA277Tnv8+MmMGTOGESMGY7FYaNu2w4M3LIQQduhi6gWG/Nifjuvasvfar3R8/CV29ohh\n5rPheDl7F3o9iprLfuqjR48SHh7O5cuX0el0lClThjZt2lC+fHnat2/Pvn37iIyMBKBDhw4MGDAA\ngMjISPbv34+iKAQFBVG9enWuX79OQEAAGRkZlCtXjtDQUBwcHHJ87eKwS8Wedu3cjfRXstl7f2D/\nPUp/xYuqqpxKOskvV3aw6/JOtpz7gQxrBk/51Gd6s1k083v2jnXyu8d77R7PNbSLUnF4o0vaD9z9\nkv5KNnvvD+y/R+mvaKmqytmU0/xyeSe7L+9k15VfuG6Oy36+ontlAp4O5D9Vu6NR7r5zujBDW66I\nJoQQ4pHzR2IsH/++hB/Pb+Kq6Ur24776MnSr8irNyrXgWb8WPF7KH0XJ37OUHoaEthBCiEeC1WZl\ny/lNLD3yETsv/wxAaRcfuvh3o7lfC571a4m/x5PFKqT/TUJbCCGEXUvJSGbVsRUsO7qYCzfPAdCi\nfCsG1x1Ku4odCvXo74cloS2EEMIunU46xZLfFxJ9/AvMFhMuOhf61HyTgXXeooZ3zaIu74FIaAsh\nhLA7x28co/2almRYM/AzlGdMnQB61ehTJKdp5ScJ7ft09eoV+vbtQbVq1QHIzMykV6//47nnWt/3\nWOvWRZOcnEzLlq3YsWM7Awa8ddfl/ppW816nx/3l7NnTREVF3DGd53PPPUOdOk9l3/f29mb69ND7\nrvnftm3bSuvW7Th16sQ9exBCiMI0Z184GdYMQp6NoF/tgeg09hF39tFFIatYsVJ2KN68mcKbb/ai\nSZOmODk5P9B4VapUo0qVajk+/9e0mnkJ7ZwYDIZ8mZf731as+JTWrdvl2oMQQhSWEzeOs/HMBur6\n1GNAnbeK9YFl90tC+yG5u5fC27s0iYmJLF++BJ3OgZs3k5kxI4yIiFlcuXIZi8XCwIFDaNjwafbv\n38u8eXPw8vLG27s05cr5cfDgftav/5KZMyPuOa3m++8vZOPGDWzduglF0dCiRSveeKM316/HMWXK\nBBwcHHjyyap5rv3q1Su89dZEFi36FIABA/owc2Y4H3+8mNKlfThx4hhxcdeYOnUm1apVZ+XKT9m+\n/ScURcOQISM4fvwPTp8+SWDgOF599fXsHn766Ueio1ei1WqpVq0Go0aNZdmyRXedRlQIIfJb1P5w\nVFTGNppgV4ENJTy0XadNxumb/J2aM6NzV0zT8j4159WrV7h5MwVf3zLArWt6BwRMYtOm7/D2Ls3E\niVNJTk7mnXeG8Omnq1m0aD5TpgRTpUpVxo59m3Ll/LLHMptN95xWMz7+Otu3/8SHHy4DYOjQAbRu\n3Y7166Np27YD3bu/wYoVn3D69MmH/nvIzMwkKmo+X321lk2bvkOv17N9+08sWvQJV65cZsWKT5gw\nYQorV35KSMhsDh7c/78ezCxevIDly1eh1+sZP/7d7Of+PY2ohLYQIr+duHGcr06vp07pp3i+csei\nLifflejQLioXLpxnxIjBwK35xidPnp49fWnNmremJD169AiHDx/iyJHfAMjIyCArK4urV69Spcqt\nreF69RqQkZGRPe65c39SsWJlnJyccXJyJiws6rbXPXYslkuXLjJy5K3vjc1mE9euXeHcuT9p3frW\n/OX16zfi119331Gz0WjMrhnA3/9JevTonWOPTz1VHwAfnzL88UcsJ0+eoGbN2mg0GsqXr8CECVPu\nut7FixcoX75i9ixl9es35OTJ4wDUrVsPuDXRjNFozPG1hRDiQc09EIGKyphGAXa3lQ0lPLRN02be\n11Zxfvnnd9r/ptM5ZP/Zt29/2rd/4bbnNZq/L4P37yvIajRaVNWW4+vqdA40bdqc8eMn3fb4ypWf\novzv8no5rX+377SvXbt6232LxZJ9+6/5vP+qU6vVYLPlfsVbRbm9L4slCycnp7uOKYQQ+elU0kk2\nnFpH7dJ16fh4p6Iup0A81CxfImc1a9bml19uXXEnKekGixYtAKB0aR8uXDiHqqocOnTgtnVym1az\nWrUaHDx4gPT0dFRV5b33IsnISKdixUocP/4HQPau6LzQ611JTExEVVUSExO4cuVSjstWq1aD338/\njMVi4caNRCZOHAtwR5BXqFCJS5cuYDabADh06CDVqpXM8yGFECXLnP99l22vW9lQwre0i7M2bdpx\n8OA+hgzpj9VqpX//W7umBw8exuTJATz2WNns78H/8s9pNQFef73nbdNqfvDBYrp3f4Phwweh0Who\n2bIVTk7OvPbaG0yZMoEdO7bh718lzzW6u7vTrFkzBg7sy5NPVrnn0d9ly5bj+edfZMSIwaiqyltv\nDQegatVqDBrUl6FD387uYfjwdxgzZiSKoqFu3Xo89VQ99u+Pua+/PyGEuB+nk07x1el11PSuXThb\n2TYbzl+swPnz5bBkMVTI++/ehyGzfOWiuM9Q87Ckv5LN3vsD++9R+ssfw7YOYu3JaD5+fgUv+b9c\noK+l/f0IbgGjcdi/F5urAc2On4nPx9C+1yxfsntcCCFEiXYm+RTrT62hhlctXnzipQJ7HeVmCq6B\n4/Bs3xKH/XtJ79KNpN37oUGDAnvNf5Pd40IIIUq0qP2zsak2xj4dkOOc1w9FVXFa9yWGoElo4q9j\necIfY9gcslq1yf/XyoWEthBCiBLrbPJp1p36khpeNen0RP7vFteeOI5hwhgcd+1EdXbGNHEK5mFv\nw//OiilsEtpCCCFKrLkHIrGpNsY0yuetbKMR1znhuCxagGKxkPF8R4wzw7FVqpx/r/EAJLSFEEKU\nSGdTzrD2ZDTVvWrwkn+X/BlUVXH8diOGKRPQXrmMtUJFjLMiyHzhxfwZ/yFJaAshhCiR3jsQiVW1\n5ttWtvbsaQwTx+G47SdUR0dMo8dhfnsM/O8Kj8WBhLYQQogS59ere1hzYjXVPKvT2b/rww2WloZ+\nXhT6D+aiZGaS+VxrjGGRWO/juheFRUJbCCFEiWDOMvP16fV8EruUQ9cPAjC+ceBDbWU7/rgJw8Tx\naC+cw1q2HMbgUDI7d711TeZiSEJbCCFEsXY66RSfxi5j9YlVpGQko1E0vFD5RfrXGUyrCg922pXm\n4gUMkwJw2vQdqlaLedjbmMcGoBpyvrBJcSChLYQQotjJsmax6dx3fHJ0GTsv35rHwVdfhtENx9G7\nZj/Ku1V4sIEzMtAv/AD93NkoaWlkNm2OMWwO1holY44ECW0hhBDFyr5rMYzeNpITSbem9X3WryX9\nag2g4+Mv4aB1eOBxHXZsxzBhDLrTp7CV9iF19ntkvNaj2O4KvxsJbSGEEMWCMTOVWTHT+fj3JQD0\nqdmPt+oOp6pXzpMZ5YXm2lVcp07E+av1qBoNaQMGY5owGbWUR36UXagktIUQQhS5rec3M+7nd7ls\nvEQVj6pEtZ7PM2WbPNygFgsuSz9CHxGKxphKVoOGGCPmYqlbL3+KLgJ5Cu2QkBAOHz6MoigEBgZS\nt27d7Oe2bt3KwoULcXR0pFOnTvTu3Zs1a9awcePG7GWOHj3KoUOH6NOnD2azGf3/znkLCAigdu3a\n+dySEEKIkiIhLYHJvwSw/tQadBodoxuN592G43DSPtxlQnW/7sEtYDS6Y7HYPD1JnTOP9F59QVOy\n58nKNbT37t3L+fPniY6O5syZMwQGBhIdHQ2AzWYjODiYDRs24OHhwaBBg2jXrh2vvfYar732Wvb6\nP/zwQ/Z4oaGhVK1atYDaEUIIURKoqsrak9FM2TWBG+k3aODbkKjW86npXeuhxlXi4zEET8V59UoA\n0nr2wTRlBqq3d36UXeRy/cixZ88e2rVrB4C/vz8pKSkYjUYAkpKScHd3x8vLC41GQ5MmTdi9e/dt\n6y9YsIBhw4YVQOlCCCFKmkxrJt+e2ch/NnZm+E+DSbekE9w8lO+6bX24wLZacV6+FK9mDXFevZKs\n2nVJ+u5HjO8tsJvAhjxsaSckJFCr1t9/kV5eXsTHx2MwGPDy8sJkMnHu3Dn8/PyIiYmhcePG2cse\nOXKEsmXL4uPjk/3YvHnzSEpKwt/fn8DAQJydnfO5JSGEEMXNiRvHWXnsM9aeXE1CWgIArSu0JeK5\nuVRyr/xQY+t+O4hh/Ls4/HYIm5s7xlnhpL05CHT2d9jWfXekqmr2bUVRCAsLIzAwEDc3N8qXL3/b\nsmvXruWVV17Jvt+3b1+qVatGxYoVCQoKYuXKlQwYMCDH1/L01KPTae+3xHzn41O8T7Z/WNJfyWbv\n/YH992iv/d3MuMmSA0tYdmgZMZdjAPB28WbUM6PoX78/dcrUebgXSEqCwEBYtAhUFXr1QjN7Noay\nZTHkQ/33o7Dew1xD29fXl4SEhOz7169fv23LuXHjxqxatQqAOXPm4Ofnl/1cTEwMkydPzr7fvn37\n7Ntt2rTh+++/v+drJyWZ89BCwfLxcSM+PrWoyygw0l/JZu/9gf33aI/9pWbeZOquQDacWovZYkZB\noU3FdvSq0ZcOlTtmH2T2wH3bbDh9+QWGGVPQJCRgqVoNY9gcsp5teev5Qv77zO/38F4fAHL9Trt5\n8+Zs3rwZgNjYWHx9fTEY/v4MM3DgQBITEzGbzWzbto2mTZsCEBcXh6urK46OjsCtLfR+/fpx8+ZN\n4FagV6lS/C7GLoQQ4uFM3DmOlcc+o7SLDzNazeBgn1hWv7Sezv5dH/qocG3sUTxefgH3t4eimM0Y\np8wg6b+7/g5sO5frlnaDBg2oVasWPXr0QFEUgoKCWL9+PW5ubrRv357u3bvTv39/FEVh8ODBeHl5\nARAfH599G27tSu/evTv9+vXDxcWFMmXKMHLkyILrTAghRKH75szXfHniC57yqc/33bZS7jGvfNkK\nVVJvoo8IxWXpRyhWKxmdXsYYHIqt/ANezrSEUtR/fkldzBSHXUb2uOvqn6S/ks3e+wP779Ge+osz\nXeO56CaYs8z81P0XqnhWffj+VBWnr9bhOjUQbdw1rJUfJzUskqw27XNft5AU5u5x+zu0TgghRKFT\nVZV3t43gRvoNQp6NoIrnw1+PQ3v6FIaAMTju3I7q5IRp3ETMI9+FR/isIwltIYQQD+3zPz5h64Ut\ntCzfmv51Bj/cYGYzrnNn4/LhPJSsLDLadcA4KwLb40/kT7ElmIS2EEKIh3I25QxTd02klJMH89p8\niEZ5wEuFqiqOm77HMDkA7cULWP3KY5wVQWbHTiVqJq6CJKEthBDigVlsFkZsfQuzxcxHrT+gnMEv\n95XuQnPuTwyTxuP042ZUBwfMb4/G9O44cHXN54pLNgltIYQQD2z+offYH7eXrk92o1uV1+5/gPR0\n9AveR//+HJT0dDJbPIcxbA7WKjJHxd1IaAshhHggR+J/I2JfCI+5liW8ZdR9r++w7ScME8ag+/Ms\nVt8ymN7/kIyu/5Fd4fcgoS2EEOK+pVvSGb51MBabhfdaL8DT2Sv3lf5Hc+UyhikTcfrmK1SNBvPg\noZjHB6K6lyrAiu2DhLYQQoj7NitmOieSjtO/9iDaVGyXt5WysnBZ9CGukWEoZhNZTz9DangU1toP\neQ3yR4iEthBCiNt8dWodOy//jE21oaoq2f/977bFlsX6U2vx93iSqU2D8zSmw+5fbu0KP34Mm7c3\nxpAI0nv0As0DHmn+iJLQFkIIkW3ewbnM/DUo1+UMDm4saLsYvYP+3gteu4bbyFE4r41GVRTS+vbH\nNGkqqmfed6eLv0loCyGEAGDO/nDC987Cz1CexR2W4+XshYICikL2f/+77ensiZuje86DWa04f7IU\nQoNxvnmTrKfqYwyfg6VBo8JryA5JaAshxCNOVVXC9gYz90AkFd0qsb7Lt1R0r/TA4+n278UQMAaH\n3w+Dhwep4VGk930TtNp8rPrRJKEthBCPMFVVmbFnKgt+e5/K7o+zoct3+LmVf6CxlBuJuM6chsuK\nTwFI7/4Gzh+8R7riko8VP9oktIUQ4hGlqipTdk1g8ZGFPOlRhfVdvuUx17L3P5DNhvOqz3ENnoom\nKQlLjZoYw6PIatIMZx83sJNZzIoDCW0hhHgE2VQbATvG8GnsMqp71WDty9/gq/e973F0vx/GMH40\nDgf2YXM1YJweQtrAt8DBoQCqFhLaQgjxiLHarIzZ/jarjn9OLe86rHn5a0q7lL6vMZSbKejDZuLy\n8RIUm430rt0wTQ/BVrZcAVUtQEJbCCEeKeYsM2N/foe1J6N5yqc+X3becF9XM0NVcVobjWHaZDTx\n17H4P4kxbA5Zz7UuuKJFNgltIYR4RGw9v5kJO8ZyIfU8Dcs0YvVL6ynl5JHn9bXHj2GYMAbH3b+g\nurhgCpyKeehIcHIqwKrFP0loCyGEnbtmusrkXyaw8cwGdBodI+qPYmyjCblfGOUvRiOukWG4LP4Q\nxWIh44UXMc4Mx1bxwU8LEw9GQlsIIeyU1Wblk9ilhMQEk5p5k0ZlGhPZ6n1qetfK2wCqiuO3X2OY\nMhHtlctYK1bCOCuCzOc7FmzhIkcS2kIIYYd+jz/M2J/f4dD1g5Ry8iDyuffpXfP/0Ch5u9a39uxp\nDBPG4rj9v6iOjphGj8P89hjQ53HrXBQICW0hhLAjaZY0QmOCWXzkQ2yqjW5VXmNG89C8n86Vlob+\n/Tno57+HkplJZqs2GENnY/WvUrCFizyR0BZCCDthsVkYuLkvP57fzOOlniC8ZRStKrTJ8/qOW37A\nEBiA9sI5rGXLYQwOJbNzV1CUAqxa3A8JbSGEsAOqqjJ2+zv8eH4zrSu05ZOOq3DR5e3yoZqLFzBM\nCsBp03eoOh3mYW9jHhuAanAr4KrF/ZLQFkIIOxC2N5hVxz+nnk99lr3wed4COyMD/cIP0M+djZKW\nRmbT5hjDo7BWr1HwBYsHIqEthBAl3LLfFzP3QCSPl3qClZ3WYnAw5LqOw47tGCaMQXf6FLbSPqTO\nfo+M13rIrvBiTkJbCCFKsG/OfEXgznH4uPgS/dIGfPQ+91xec+0qrkGBOG9Yh6rRkDZgMKYJk1FL\n5f0iK6LoSGgLIUQJtevyTob+OBBXBwOrX1pH5VKP57ywxYLL0o/QR4SiMaaS1aAhxoi5WOrWK7yC\nxUPLU2iHhIRw+PBhFEUhMDCQunXrZj+3detWFi5ciKOjI506daJ3797ExMTwzjvvUKXKrVMEqlat\nypQpU7h69Srjx4/HarXi4+PD7NmzcXR0LJjOhBDCjsUmHKXvD2+gorL8hRXU8Xkqx2V1v+7BLWA0\numOx2Dw9SZ0zj/RefUGTt3O2RfGRa2jv3buX8+fPEx0dzZkzZwgMDCQ6OhoAm81GcHAwGzZswMPD\ng0GDBtGuXTsAGjduzLx5824ba968efTs2ZOOHTsSFRXF2rVr6dmzZwG0JYQQ9uti6gV6fNuN1Myb\nfNR+Gc9VuPtkHUp8PIbgqTivXglAWq++mCZPR/X2LsxyRT7K9WPWnj17soPY39+flJQUjEYjAElJ\nSbi7u+Pl5YVGo6FJkybs3r07x7FiYmJo27YtAK1bt2bPnj350YMQQtg1m2rDmGUkzhzH8RvHeP2b\nV4gzX2NG8xC6VXntzhWsVpyXL8WrWUOcV68kq3Zdkr77EePc+RLYJVyuW9oJCQnUqvX3dWq9vLyI\nj4/HYDDg5eWFyWTi3Llz+Pn5ERMTQ+PGjfHz8+P06dMMGTKElJQURowYQfPmzUlLS8veHe7t7U18\nfHzBdSaEECXMpdSLzPx1GsdvHMOUZcSUZcKcZcJsMd+x7PB67zDkqRF3PK777SCG8e/i8NshbG7u\nGGeFk/bmINDJIUz24L7fRVVVs28rikJYWBiBgYG4ublRvnx5ACpXrsyIESPo2LEjFy9epG/fvmzZ\nsiXHcXLi6alHp9Peb4n5zsfHvi8wIP2VbPbeH9h/j17eeubvnc+k/07ClGXCzdENdyd3vPVeVHSs\ngMHRgMHRgKuDKwZHA0+VeYqRz4y8/TriSUkQGAiLFoGqQq9eaGbPxlC2LLmfAFaw7P39g8LrMdfQ\n9vX1JSEhIfv+9evX8fH5+5SCxo0bs2rVKgDmzJmDn58fZcqU4cUXXwSgYsWKlC5dmri4OPR6Penp\n6Tg7OxMXF4ev772vhZuUdOeny8Lm4+NGfHxqUZdRYKS/ks3e+wP77/Gq7U/eXN+fg9cP4OnkSWib\nSF6v1hMll/OlExNMt27YbDhFr8IwYwqaxEQsVathDJtD1rMtbz1fxH939v7+Qf73eK8PALl+p928\neXM2b94MQGxsLL6+vhgMf39uGzhwIImJiZjNZrZt20bTpk3ZuHEjy5YtAyA+Pp7ExETKlClDs2bN\nssfasmULLVq0eKjGhBCipEqzpDHr1+k0XNyQg9cP0K3Kq/zyxn56VO+Va2D/RRt7FI+XX8D9nWEo\naWkYp8wg6b+7/g5sYXdy3dJu0KABtWrVokePHiiKQlBQEOvXr8fNzY327dvTvXt3+vfvj6IoDB48\nGC8vL9q0acPYsWP56aefyMrKYtq0aTg6OjJy5EgCAgKIjo6mXLlydO3atTB6FEKIYuWXyzsYs/1t\n/kw5S8VSFQl/Noq2lTrkeX0l9Sb6iBBcli5CsVrJeKkLxuBQbH7lC7BqURwoal6+XC4ixWGXir3v\n2pH+SjZ77w/sq0dzlpnAneNYdfxzNIqGQXWHEvliGGkpefw1rKo4fbUO16mBaOOuYXn8CYyhkWS1\naVewhT8Ee3r/clKYu8flcEIIDT6cAAAgAElEQVQhhCgENzNS6PV9d2Ku7qGWdx2iWs2jfpmGGBwN\npJH7L3ztyRMYJo7FcefPqM7OmAImYR7+Djg7F0L1oriQ0BZCiAJ2Iz2R17/pxuH4Q3R9shvz2y7G\nUZvHq0GaTLjOnY3Lwg9QsrLIaP88xlkR2Crf45Klwm5JaAshRAGKM13jtW+6cPzGMXpW78OcVvPQ\navJwKquq4vjDdxgmB6C9dBFr+QoYZ0WQ+cKLMhPXI0xCWwghCsjF1Au8uvFl/kw5y6A6Qwh+Nuz2\nc6tzoDn3J4bAcTht3YLq4ID5nTGYRo0FV9dCqFoUZxLaQghRAM4kn+LVjV24bLzEuw3HMqHxlNxP\n5UpPRz//PfTvz0HJyCCzRSuMYZFYq1QtnKJFsSehLYQQ+eyPxFhe29iF+LTrTG4ynbcbvJvrOg7/\n/RG3CWPRnvsTa5nHMAWHktGlm+wKF7eR0BZCiHx0MG4/Pb7tRnJGMqEtIhlQZ/C9V7h4EfehI3D6\nbiOqVov5reGYx09EdXMvnIJFiSKhLYQQ+SDNksb6k2uYvGsCaRYz89ospEf1XjmvkJmJy0cLICoc\nJ7OZrMZNSA2PwlqrduEVLUocCW0hhHgIF1MvsPzoUlb+8SlJGUk4ahxZ0uETOvvnfMVHh107MQSM\nRnfyBPj4cDNsDhnd3wBN7gepiUebhLYQQtwnVVXZeflnlv6+iC3nfsCm2vB29uadBmP4v1r9Ke9W\n4a7rKXFxGKZNwnndl6iKQlq/AbhEzSbDIr+KRd7IT4oQQuSRMcvIlye+4OPfF3My6QQA9XzqM6DO\nW3R5shvOuhyuTmax4LJ8CfqwWWhSb5JVrz7G8Cgs9Rvi4ulW5DNxiZJDQlsIIXJhtVlZeewzwvYG\nk5CWgIPGgf9U6c7Aum/RwLfRPU/l0u2LwRAwBoejR7CV8iA1PIr0vm+CNg8XWBHiXyS0hRDiHnZe\n+pkpuybyR+JR9DpXxjQK4M3ag/DV+95zPSUxEdeZQbis/AyA9B69ME6ZgerjUxhlCzsloS2EEHdx\nNvk00/ZMYdOf36Gg8Eb13gQ+M5Uyro/de0WbDecVn+I6axqapCQsNWqRGh6FpUnTwilc2DUJbSGE\n+IeUjGSi9s9m6e8fkWXL4pmyTZnZPIynfOvnuq7uyG8YAkbjcGA/NlcDxhkhpA0cAjr5VSvyh/wk\nCSEEt763/vyPTwjfO5PE9EQqulUiqFkwLz3RJdfLjyopybiGBuP8yTIUm430rt0wzQjF9ljZQqpe\nPCoktIUQj7yYq78ycedYjiYcwdXBwOQm0xhcd1jOR4P/RVVxWrMaw7TJaBLisTxZBWPYHLJatiqU\nusWjR0JbCPHIijPHEbxnKl+e+AKA7tXeYEqT6bl/bw1oj/2BYcIYHPfsQnVxwTgpiLQhI8DJqaDL\nFo8wCW0hxCMny5rFsqOLiNgbijErldql6xLaIpJnyjbJfWWjEdfIMFwWf4hisZDR8SWMwaHYKlYq\n+MLFI09CWwjxSPnl8g4m7hjLiaTjeDh5EN4yir4130SryeW8aVXF8duvMUyegPbqFawVK2MMjSCz\n/QuFU7gQSGgLIR4R8eZ4AneO4+sz61FQ6FPzTQKfmYq3i3eu62rPnsYwYSyO2/+L6uiIaUwA5rdH\ng4tLwRcuxD9IaAsh7N4vl3cw5McBXDfH0bBMI0JbRFLPt0HuK6aloX8/Ev3891EyM8ls3RZj6Gys\nTzxZ8EULcRcS2kIIu2W1WZl7YDaR+8PQKBqCms5kaL0RaJTcZ9Ny3PIDhsAAtBfOYS3nhzE4jMyX\nXoZcTv8SoiBJaAsh7FKcOY5hPw5k5+WfKW+owOIOy2n0WONc19NcOI9hcgBOm75H1ekwD38H05gA\nMBgKoWoh7k1CWwhhd3Zc2s7QHwcSn3adFyq/yPttPsTT2eveK2VkoF/4Afq5s1HS0shs2hxjeBTW\n6jUKp2gh8kBCWwhhN6w2K5H7w4jaH4FWo2VG8xDeqjs81yuaOfy8DcOEMejOnMbm40tq5PtkvPq6\n7AoXxY6EthCiRFJVFWNWKknpSSRnJHEj/QbzDkbxy+UdVHCryOIOy2lY5ul7jqG5egXXqYE4f70e\nVaMhbcBgTBMmo5byKKQuhLg/EtpCiGIv3ZJOSMwM9l/bS3LGrZBOSk/CqlrvWLbj4y/xfusFeDh7\n5jxgVhYuSxehjwhBYzKS1bARxvAoLHXrFWAXQjy8PIV2SEgIhw8fRlEUAgMDqVu3bvZzW7duZeHC\nhTg6OtKpUyd69+4NQEREBAcOHMBisfDWW2/RoUMHJkyYQGxsLB4etz7FDhgwgFatWuV/V0IIu5Fg\nTuC1b7oQc3UPOo0ODydPPJ28eLyUP55Onng4e2b/WdWzWq4TfDj8uhtDwGh0x/7A5ulJavAHpPfs\nA5rcjygXoqjlGtp79+7l/PnzREdHc+bMGQIDA4mOjgbAZrMRHBzMhg0b8PDwYNCgQbRr145z585x\n6tQpoqOjSUpK4pVXXqFDhw4AjB49mtatWxdsV0IIu3Am+RR9Vr/O6Run6fpkN+a1+Sj3STxyoMTH\nY5gxBefoVQCk9f4/TJOmoXrnfnEVIYqLXEN7z549tGvXDgB/f39SUlIwGo0YDAaSkpJwd3fHy+vW\nUZlNmjRh9+7ddOnSJXtr3N3dnbS0NKzWO3djCSFETvZc2UW/H3qSlJHEqAZjmfDM5DydX30HqxXn\nTz/GNTQYTUoyWXWewhg+B0uj3E//EqK4yTW0ExISqFWrVvZ9Ly8v4uPjMRgMeHl5YTKZOHfuHH5+\nfsTExNC4cWO0Wi16vR6AtWvX0rJlS7TaW9f1XbFiBcuXL8fb25spU6ZkB/7deHrq0elyuR5wIfDx\ncSvqEgqU9Fey2WN/K46soP/G/qioLHt5Gf3r93+wgfbtg6FD4cABcHeHefNwGDoUT13xOpzHHt/D\nf7L3/qDwerzvn1xVVbNvK4pCWFgYgYGBuLm5Ub58+duW3bp1K2vXruXjjz8GoEuXLnh4eFCjRg0W\nL17M/PnzmTp1ao6vlZRkvt/y8p2Pjxvx8alFXUaBkf5KNnvrT1VVIveHMXtfKO6Opfj4hc/5T/3O\n992jknQD11kzcP58OYqqkv7q6xiDZqKWKQNJaQVU/YOxt/fw3+y9P8j/Hu/1ASDX0Pb19SUhISH7\n/vXr1/Hx8cm+37hxY1atuvUd0Zw5c/Dz8wNg586dfPTRRyxduhQ3t1sFNG3aNHu9Nm3aMG3atPvr\nRAhhtzKsGYzeNpI1J1dT0a0SKzutoZpX9fsbxGbDKXoVhhlT0CQmYqlWHWPYHLKatyiYooUoZLl+\nQdS8eXM2b94MQGxsLL6+vhj+cTm/gQMHkpiYiNlsZtu2bTRt2pTU1FQiIiJYtGhR9pHiACNHjuTi\nxYsAxMTEUKVKlfzuRwhRAhkzU3n9m1dYc3I1Dcs04vv//HTfga09+jsenZ/H/Z1hKGnpGKcGk/Tf\nXRLYwq7kuqXdoEEDatWqRY8ePVAUhaCgINavX4+bmxvt27ene/fu9O/fH0VRGDx4MF5eXtlHjY8a\nNSp7nPDwcHr16sWoUaNwcXFBr9cTGhpaoM0JIYq/LGsWAzb3ZfeVX3jpiS4saLcYF13ep7xUUm+i\njwjBZekiFKuVjJe6YAwOxeZXPveVhShhFPWfX1IXM8XhexB7/z5G+ivZSnp/qqoyevtIVh77jPaV\nnufTjl+g09y+LZFjj6qK04a1uAZNQht3DcvjT2AMnU1Wm/aFVH3+KOnvYW7svT8oZt9pCyFEQZl7\nYDYrj33GUz71WdRh+R2BnRPtyRMYJo7FcefPqM7OmAImYR7+Djg/2DncQpQUEtpCiCIRfXwVYXtn\nUsGtIis6fYnBIQ9TX5pMuM6djcvCD1Cyssho/zzGWRHYKj9e8AULUQxIaAshCt2OS9t5d/sISjl5\n8EWndZTRl7n3CqqK4w/fYZgcgPbSRawVKmKcGU7mCy/KTFzikSKhLYQoVH8kxvLmpt5o0PBZxy+o\n6lXt3iucPYv7W0Nx2roF1cEB06ixmEeNhf9dwEmIR4mEthCi0Fw1XqHnt6+SmnmTRe0/pmm55jkv\nnJ6O/oO5MC8Kp4wMMlu0whgWibVK1cIrWIhiRkJbCFEoUjNv0vO717hiusyUpjN4pcqrOS7r+NMW\nDBPHoT33J5Qty83pIWR06Sa7wsUjT0JbCFHg0i3pDNjcl9jE3+lXawAj6r1z1+U0ly9hmDwBp+82\nomq1mN8ajj4ihIwMCWshQEJbCJHPEtMSiU38naMJvxObcOvPU8knsNgsdKj0AiEtZt8533VmJi4f\nLcA1KhzFbCarcRNSw6Ow1qqN3t0N7Pw8XyHySkJbCPHQNp7eQPSJVcQmHOWK6fJtz+l1rtTzaUDj\nsk0Y9/TEO87Fdti1E0PAaHQnT2ArXZrUsDlkdH8DNA8wDacQdk5CWwjxUJYe+YjAX8YDUNa1HO0q\ndqB26brULl2H2qXrULnUE3edB1sTdw3XoEk4r1+Dqiik9RuAKXAqqodnYbcgRIkhoS2EeGAf/vYB\n03ZPwldfhi87f0VN71q5r2Sx4PLxYvThIWhSb5JVrz7G8Cgs9RsWfMFClHAS2kKIB/L+gTnMiplO\nWddyrO/yDf4euc/ap9sXg9v40ehif8dWyoPUiLmk9+kHWm3BFyyEHZDQFkLcF1VVidwfxux9oZQ3\nVGBdl294vNQT91xHSUzENXgqLqs+ByC9Ry+MU2ag+vgURslC2A0JbSFEnqmqSmhMMO8djKSie2U2\ndPmWCm4Vc17BZsP5809wnTUNTXIylhq1SA2PwtKkaeEVLYQdkdAWQuSJqqpM2z2ZhYc/4IlS/qzv\n8i3lDH45Lq87fAhDwGgcDh7A5mrAOCOEtIFDQCe/doR4UPKvRwiRK1VVmfTLeJb+vogqHlVZ3+Vb\nyrg+dtdlleQkXEODcf5kGYqqkv7KfzBND8H2WNlCrloI+yOhLYS4pyxrFhN2juXzP5ZTw6sma17e\niK/e984FVRWnL7/AMH0ymoQELE9WwRg2h6yWrQq9ZiHslYS2ECJHZ1POMPTHARy6fpDapeuypvPX\neLt437Gc9tgfGAJG4/jrblQXF4yTgkgbOhIcHYugaiHsl4S2EOIOqqoSfWIVE3eOw5Rl5LWqPQhr\nGYmbo/ttyynGVPSzw3BZ/CGK1UpGx5cwzgzDVuEeB6cJIR6YhLYQ4jYpGcmM//ldNpxeh5ujOwvb\nLeU/VbvfvpCq4rRxA65TJqK9dhVrxcoYQyPIbP9C0RQtxCNCQlsIkS3m6q8M2zqQi6kXaFSmMQvb\nL6WSe+XbltGeOYVhwlgcf96G6uiIaUwA5rdHg4tL0RQtxCNEQlsIgcVmIWp/BFEHIgAY0yiAMY0C\nbp/cw2xG/34k+gXzUDIzyWzTjtSQ2die8C+iqoV49EhoC/GIstqsnEw6wcG4/aw89hn74/ZS3lCB\nD9svpUnZ2y9+4rj5BwyB49BevIC1nB/GmeFkduoM/55iUwhRoCS0hXhExJnjOBi3P/v/Q9cPYsz6\ne57qLv7diGz1HqWcPLIf05w/h2HSeJy2bELV6TCPGIVp9HgwGIqiBSEeeRLaQti51cdXMntfKBdT\nL9z2eBWPqjR87GUa+Dbi6ceeoaZ3LZS/tpwzMtAveB/9e5Eo6elkNnsWY3gU1mrVi6ADIcRfJLSF\nsGPbLvzEqG3DcdHpaV/peRqUaUTDMk9T37fBbVvU/+Sw7ScME8eiO3sGm48vqVEfkPGf7rIrXIhi\nQEJbCDt1OukUg7b0Q6foWNP5Kxo91viey2uuXMZ1aiDOGzegajSYBw3BHDAJ1b1UIVUshMhNnkI7\nJCSEw4cPoygKgYGB1K1bN/u5rVu3snDhQhwdHenUqRO9e/fOcZ2rV68yfvx4rFYrPj4+zJ49G0e5\nYpIQ+S45PYk+P7zOzcwUPmjz0b0DOysLlyUf4RoRgmI2kdWoManhUVjr1M15HSFEkdDktsDevXs5\nf/480dHRzJo1i1mzZmU/Z7PZCA4OZsmSJaxcuZJt27Zx7dq1HNeZN28ePXv2ZNWqVVSqVIm1a9cW\nXGdCPKIsNguDtvTjTPJpRtQfxevVe+a4rMOeXXi2fRbDtEmozk6kzp1P8rdbJLCFKKZyDe09e/bQ\nrl07APz9/UlJScFoNAKQlJSEu7s7Xl5eaDQamjRpwu7du3NcJyYmhrZt2wLQunVr9uzZU1B9CfHI\nmrZ7Ej9f2kb7Ss8z6Zmguy6jXL+O2/DBeHTpiPbEcdL69OPG7gOk9+oLmlx/LQghikiu/zoTEhLw\n9PTMvu/l5UV8fHz2bZPJxLlz58jKyiImJoaEhIQc10lLS8veHe7t7Z09jhAif6z441MWH1lINc/q\nfNR+GVqN9vYFrFacly3Gq1lDnNesJqvOUyR/vxXjnHmoXndOBCKEKF7u+0A0VVWzbyuKQlhYGIGB\ngbi5uVG+fPlc17nXY//m6alHp9PmulxB8/FxK+oSCpT0V7L91d+O8zsI2DEaLxcvvu/zHU94+t2+\nYEwMDBsGBw9CqVIwfz4OQ4bgqS36f2O5eVTeQ3tl7/1B4fWYa2j7+vqSkJCQff/69ev4+Phk32/c\nuDGrVq0CYM6cOfj5+ZGRkXHXdfR6Penp6Tg7OxMXF4ev713m5P2HpCTzfTeU33x83IiPT819wRJK\n+ivZ/urv/M1zdFvbDRWVpR0+w83ik923knQD15nTcV7xCYqqkv5aD4xBM1F9feFG0f8by82j8h7a\nK3vvD/K/x3t9AMh193jz5s3ZvHkzALGxsfj6+mL4x9WQBg4cSGJiImazmW3bttG0adMc12nWrFn2\n41u2bKFFixYP1ZgQAoyZqfT9vgeJ6YmEPDubZ/1a3nrCZsN55Wd4NW2Ay+fLsVarTvLXP5C6YPGt\nwBZClDi5bmk3aNCAWrVq0aNHDxRFISgoiPXr1+Pm5kb79u3p3r07/fv3R1EUBg8ejJeXF15eXnes\nAzBy5EgCAgKIjo6mXLlydO3atcAbFMKembPMDN7yJsdu/EH/2oPoV3sAANrfj+AWMBqH/XtR9a4Y\ng2aSNngoODgUccVCiIehqHn5crmIFIddKva+a0f6K7muma7S/8de7L+yn1YV2rDyxTU4mszow2fh\nsmwxis1G+suvYJoRgq2cX+4DFlP2/B6C9GcPCnP3uFwRTYgS6Ej8b/T5vgdXTVd4o3pvZreci+Gr\nDbgGTUJ7PQ7LE/4YQyPJat22qEsVQuQjCW0hSpjvzn7D8K2DSLOkEdEugv5qK9y6/wfHX3agOjtj\nmjAZ8/B3wMmpqEsVQuQzCW0hSghVVfng0Fxm/joNvU7PilYf0/Ob46hzmqFYLGQ83xHjzHBslSoX\ndalCiAIioS1ECZBhzWDM9rf58sQXlNOXY5PTcGr2mgKXL2GrUBHjrAgyX3ixqMsUQhQwCW0hirmE\ntATe3NSLmKt76KzUYuX33rhtn4Tq4ACTJnFj0EjQ64u6TCFEIZDQFqIYybRm8mfKWU4mneB00klO\nJp1g15WdJCVf5Ys/qvP696dRMmLJbNkaY1gkXk0bgJ0fmSuE+JuEthBFKM50jY+PLubYjWOcSjrB\nuZQ/sarW25bpctaRpT96UPrqcayPlcUUHErGy6+AohRR1UKIoiKhLUQRiTfH0/XrFzmTfBoADycP\nGpRpRFXPajzpUZV6GV4898FaPH/8L6rWinnICMzjJ6Ia7P86zkKIu5PQFqII3MxIoce33TiTfJoh\nT41gRP1R+Lj4oCgKZGbi8tECXKPGopjNZD3TlNTwKKw1axV12UKIIiahLUQhM2eZ6fV9d35POEyf\nmm8yvdmsW2ENOPyyA8OEMehOnsBWujSp4VFkdH9DdoULIQAJbSEKVaY1kwGb+xBzdQ9dn+xGRMso\nFEVBE3cN16BAnNevRVUU0t4ciGniFFQPz9wHFUI8MiS0hSgkVpuVET8N5qcLP9K2Ynvmt12M1qbi\nsvRD9GGz0BhTyarfAGN4FJZ6DYq6XCFEMSShLUQhUFWV8TtG89Xp9TR+rAnLnv8c/YFDuAWMRhf7\nOzYPD1Jnv0d67/8DrbaoyxVCFFMS2kIUgpm/TuPzP5ZTu3RdvmiyEN9x43BZ9TkAaW/0xjRlBmrp\n0kVcpRCiuJPQFqKAzTs4lw8OzcXf7Qk2p7zGY61ao0lOxlKzNqnhUVieaVLUJQohSggJbSEKiKqq\nLDqygJm/BvF8kg/rNrjiengKNoMbxplhpPUfDDr5JyiEyDv5jSFEAbhmusq720Zw4MSPLNvhzJu/\nJqCo8aR3exXTtFnYHitb1CUKIUogCW0h8tlXp9Yx/udRdN6bwpqfHPBMTcdSpSrGsDlktXiuqMsT\nQpRgEtpC5JOk9BtM2DGGk7vW8c33Gp49D6qLA8bJk0gbMgIcHYu6RCFECSehLUQ++On8Fib9MIyh\nP1znyxjQ2WxkdHwJ48wwbBUqFnV5Qgg7IaEtxEMwZhkJ+iWQ9DWfsGMz+KWCpVJlUkJnk9nu+aIu\nTwhhZyS0hXgAcaZrrDr2OTu3L2LK2ut0OAtWR0dMY0djHvkuuLgUdYlCCDskoS1EHtlUG9sv/pfP\nYpez4+R3BOywsXU3OFkhvXUbTKFzsD3hX9RlCiHsmIS2ELmIM8ex+tgKPj/2KRdunuOlE3BsiwPl\nE21YypUjZWYEmZ06y0xcQogCJ6EtRA5O3jhBxL4Qvv/zGyw2C9VvOrH/5/I0PHAJVadiHvkuptHj\nwdW1qEsVQjwiJLSF+BdjZiqR+8NZfORDLDYLdd1qMC+2Ei1WbkOTcYnM5i0whs3BWq16UZcqhHjE\nSGgL8T+qqrLu1JdM3z2FOPM1KrpXZqnuDVq/vwbdmU3YfHy5OSOEjG6vya5wIUSRkNAWAjia8DuB\nO8fx69XdOGudmfX4CN5ZewHXb0JRNRrMg4ZgDpiE6l6qqEsVQjzC8hTaISEhHD58GEVRCAwMpG7d\nutnPrVy5ko0bN6LRaKhduzaTJk1i4cKF7N69GwCbzUZCQgKbN2+mTZs2PPbYY2j/N19wZGQkZcqU\nKYC2hMib5PQkwvfNYvnRpdhUG50rdOLDU9XxG/oRitlEVsOnSY2Yi7VO3dwHE0KIApZraO/du5fz\n588THR3NmTNnCAwMJDo6GgCj0ciyZcvYsmULOp2O/v3789tvvzF06FCGDh0KwIYNG0hMTMweb8mS\nJbjKgTuiGFh38kum7JpAQloC/h5Pslj/f7ScvQrd8e+weXlhnBVO+hu9QaMp6lKFEALIQ2jv2bOH\ndu3aAeDv709KSgpGoxGDwYCDgwMODg6YzWb0ej1paWmUKvX37kOLxcIXX3zBZ599VnAdCHGfUjKS\nCdgxmvWn1qLXuRJWfTwj155Dv3YKqqKQ1udNTJOmonp5F3WpQghxm1xDOyEhgVq1amXf9/LyIj4+\nHoPBgJOTE8OHD6ddu3Y4OTnRqVMnHn/88exlt2zZwrPPPouzs3P2Y0FBQVy+fJmGDRsyZswYFDmg\nRxSiXZd3MuKnt7hsvERjn6eJjmtLxcEL0dxMIavOUxgjorA0fLqoyxRCiLu67wPRVFXNvm00Glm0\naBGbNm3CYDDwf//3fxw/fpzq1W+dCrNu3TqmT5+evfzbb79NixYtKFWqFMOHD2fz5s288MILOb6W\np6cenU57vyXmOx8ft6IuoUA9Cv1lWjOZ8t8pzN49G42iYanvIPov3Y9yMAxKlYL583EYMgRPbdH/\nvN0ve3//wP57lP5KvsLqMdfQ9vX1JSEhIfv+9evX8fHxAeDMmTNUqFABLy8vABo1asTRo0epXr06\nZrOZa9euUb58+ex1u3btmn27ZcuWnDx58p6hnZRkvv+O8pmPjxvx8alFXUaBeRT623ViP0O2DuBo\nwhHqaSvy9W+1qbB+KYqqkv5aD4xBM1F9feFG0f+83S97f//A/nuU/kq+/O7xXh8Acj3Cpnnz5mze\nvBmA2NhYfH19MRgMAPj5+XHmzBnS09MBOHr0KJUrVwbg+PHjPPHEE9njpKamMmDAADIzMwHYt28f\nVapUebCOhMgDVVVZsHcB7da0IPb6EZZcacr+qFQqrvsea7XqJH/9A6kLFt8KbCGEKAFy3dJu0KAB\ntWrVokePHiiKQlBQEOvXr8fNzY327dszYMAA+vbti1arpX79+jRq1AiA+Pj47C1wADc3N1q2bMnr\nr7+Ok5MTNWvWvOdWthAPw2qzMmhLP749+zUtEt1Yu608vkf3YHM1YJw2i7RBQ8DBoajLFEKI+6Ko\n//ySupgpDrtU7H3Xjr32F7RrEitjPmDZvnL8Z9s1FJuN9JdfwTQjBFs5v6IuL9/Y6/v3T/beo/RX\n8hXm7nG5IpqwO9HHVpLy+Qec2qrF9+YVLE/4YwyNJKt126IuTQghHoqEtrArx3etofa7wxhxDmxO\nOgieRlK/IeDkVNSlCSHEQ5PQFvbBaEQNm0qTpUtxsMHlFo1wjvoY70Z1wM53zQkhHh0S2qJkU1Uc\nv92I6+QAdFev8KcHxIzuQ9shC7AVdW1CCJHPJLRFiaU5ewa3wHE4/ncrWToNwS3hVP/uRHacX9Sl\nCSFEgZDQFsVSSkby/7d35wFR1Xsfx98zMKyDwBCQG1clt6vJg5Ep7gbmlq3XMk0NylK0TBMUDGwR\n17zaxS2Xm7cwSaSuN03QXLLErVAvdBGlVNzBBRgWYWbO84dPc/NRQFEYBr6vv5zlHL4ff5zznfM7\nhzOknNxKtybdaebS/OYXS0pw+nghTnGLUF2/zonOvgwKzKZRh0f5qn+c3BpXCFFvSdMWdU7B9Xye\n3/QUR3LTAPD36swQ36cZ0moobQ8eRzt9KjanTmJ8sDGpb75Ir+t/5UFtE5IGxONg61DF2oUQwnpJ\n0xZ1SlF5ES9t/gtHctN4osVASgyl/Hj2ey5n/Yz/1mi6ZIJRreLsKyPImTCWQclPYm/rwKcD4vF2\nftDS5QshRI2Spi3qjJAxTP8AABw4SURBVFJDKaO+Hc6BC/t45qHnWBq0ChuDET6ei9uyRWiul7Pn\nTyrGDVLI8I7Hfksi143XWRa0Cn/vRyxdvhBC1Lgq7z0uRG0oM5YRmvwye87sYkDLwcQ9/gkOP+zB\nvU83POfNx8bFjYK4FTTZc4qwESsZ1PJJbFS2TAmI4Lk2wyxdvhBC1Ao50hYWZzAZGL/9NbadSqZP\n836s7jQH3fixOHy1EUWtpiTkNYqmv4vi6kYj4Pk2L/B8mxcsXbYQQtQ6adrCokyKiUk7w9iU/RXd\nvbqxMacPbm8FotYXUt75EfRzF2Lw87d0mUIIUSdI0xYWoygKEd9P4ctjX/BKYVuWJVzD/j/RmNzc\nKFywmNKRo0EtZ3CEEOJ30rSFRSiKwsy9M9h8YDVJ37vxzP5jAJSMGEXRjPdQPDwsXKEQQtQ90rRF\nrSu4nk/s3hg0/1jD8Z1q3IqvYejwMIVzF2Lo8pilyxNCiDpLmraoNQaTgX/88ne2Jb1PbFI+Xc6B\nUeuIflY0Ja+8Brby6yiEEJWRvaSocYqi8N3pFBZun84rG0+Q8hOoFSh65llK35+DyVtuiiKEEHdC\nmraoUb9cziDmh+n8afMuNm8DryIofciX0nmLKe/Ry9LlCSGEVZGmLWrExeKLzDswiyO71hL3jULP\n02B0dEA/Yzolb4SBnZ2lSxRCCKsjTVvcd4cv/UxI4lO8vTWfNQfA1gTXBw9F/8FsTM2aV70CIYQQ\ntyVNW9xXP184yPrYIezbXELTQjC0aEn+7PmUPd7f0qUJIYTVk6Yt7pv/pG5EM+VV/n7CiMHOlqKp\nUyme+DY4yNdlCiHE/SBNW9y74mLyP3ybrn//AjsjnO76MM6LP8PUspWlKxNCiHpFmraoPkXBbusW\nNNMn4XnuIqddIWvaRPxCPsSkUlm6OiGEqHekaYtqUZ/8DW1UOPbbkilXw7weKhq/v5IBHeVrMoUQ\noqbItzGIu1NaitNHc9H1egz7bcnsbqnmkTBbvBfES8MWQogaJkfa4o5pdmxHO/0dbH/7lZIH3Bn3\npJF1HRXWDIzniRYDLV2eEELUe9K0RZUMOSexmf4mbim7MKlVfPl4U8Ieu0SBg4pPB8QT3GKApUsU\nQogG4Y6admxsLEeOHEGlUhEZGUmnTp3Mr8XHx7Np0ybUajUdO3YkKiqKpKQkFi9ejI+PDwCBgYGM\nGzeOzMxMZs6cCUDbtm1577337n8icc8uFl3gqxOJ/OfCER5J3M3r315AWwZ7m8H4wQpHG5/jIbfW\nxPWYQz+fIEuXK4QQDUaVTfvAgQOcOnWKhIQEsrOziYyMJCEhAQC9Xs/q1atJSUnB1taWkJAQDh8+\nDMCgQYOIiIi4aV2zZs0yN/0pU6awe/duevfuXQOxRHV9+9tmJu0Yz8PHrrJkM3TMhWvOtqwO6cqV\n558h1qsT7T06oNVoLV2qEEI0OFU27dTUVIKCbhxN+fr6kp+fj16vR6vVotFo0Gg0FBcX4+TkRElJ\nCa6urrddT1lZGWfPnjUfpfft25fU1FRp2nVEiaGEmB8j+XbfauK2q3npCCgqFcWjRmOIjGGozsPS\nJQohRINXZdPOy8ujQ4cO5sc6nY7c3Fy0Wi329vaEhYURFBSEvb09gwcPpmXLlqSlpXHgwAFCQ0Mx\nGAxERETg4eFBo0aNzOvx8PAgNze30p/t7u6Era3NPcS7Pzw9XSxdQo26qJzipY0v0GvLL2TtUtOo\nxASdO6NatgynLl1wsnSB96i+j199zwf1P6Pks361lfGuL0RTFMX8b71ez4oVK9i6dStarZbRo0eT\nmZmJn58fOp2OPn36kJaWRkREBKtWrapwPRW5erX4bsu77zw9XcjNLbR0GTVCURQ2nPyMhNVv8+mm\ncjpfAFMjLYUxMZSODgEbG7Dy7PV5/KD+54P6n1HyWb/7nbGyDwBVNm0vLy/y8vLMjy9duoSnpycA\n2dnZNG/eHJ1OB0BAQADp6ek8//zz+Pr6AuDv78+VK1dwd3fn2rVr5vVcvHgRLy+v6iUS9+xyyWWi\n//UaQWu28/3PN54rHTYcffQHKDIuQghRJ1V5c5Xu3buTnJwMQEZGBl5eXmi1Ny5Catq0KdnZ2ZSW\nlgKQnp5OixYtWLlyJd988w0AWVlZ6HQ67OzsaNWqFYcOHQIgJSWFnj171kgoUbnUM3tYOeV/WDp1\nO2N/hpI2rbm2aSuFcSukYQshRB1W5ZF2586d6dChAy+++CIqlYqYmBiSkpJwcXEhODiY0NBQRo0a\nhY2NDf7+/gQEBNCsWTOmTp3K+vXrMRgMzJo1C4DIyEiio6MxmUz4+fkRGBhY4wHFzS6mbsF7wkt8\nlGPiuqMdpgWz0A8PAY3G0qUJIYSogkq5k5PLFlIXzoPUl/MxqoJ8HGd/gMOaT7BR4ES/ANz/+jke\nndrWi3wVqS/jV5H6ng/qf0bJZ/3q1DltYeUUBfuNX6KNiUKde4ljHrDutR6Evb1ZvolLCCGsjDTt\neszmWCbaaVOw+3EPRgd7Zjyu5rMgL7aN+ByVNGwhhLA60rTrI70e54XzcFweh8pgoKT/AIZ0zWKH\n+lfWBy/F3UFn6QqFEEJUg3w1Z32iKNj965/oejyKU9wiTE2akv95Am+P82WH+ldCHx4r9woXQggr\nJk3byqSe+5H+G3rz5bEvbrpBjc2vJ3B98VlcQ19GnZdL0eRwruw5wPY/O7LiyBIecmvNu13ft2Dl\nQggh7pU0bStiMBmYunsSh3PTmPDd64zY/BfO52XjNHcW7r26YrfzO8r69OPq9/sonjaDfPV13vxu\nHDYqG5Y8/glOGmu/IakQQjRsck7biqzPjCfr6jGGtHqKgrIC7Lan4DJlG85XFYyNm6D/cA5lQ56C\n/7vIbPqeqZwrOsvUR6fj7/2IhasXQghxr+RI20oUlRcx98AsHG0dmd/yLVISndi8DprnK8wPhEGR\nLcnq5Wdu2P88kURiVgKdvR5hUud3LFy9EEKI+0GatpX45MhSrhRcYENWAG37D8Z+62bKugaSvfmf\nbH9tACmXf6RPQjdWHl3GOf1Zpu6ehKOtI0uCPkFjI3c7E0KI+kCmx61AXkkeRxMXkPEvNa1z92B6\nwJPC+Yu4/pcX0alUfKb0YePxL4naE07UDxHE7v+AonI9c3p9hK9ba0uXL4QQ4j6RI+06Tn3+HIUv\nBfPNmhJ8LyuUhLzGldSfuD5suHkqXKVS8XybF9gz/CBP+j5NUbmefj5BvNLhVQtXL4QQ4n6SI+26\nqrwcx1UrcJz3IV2KijnsY0+TlVtQ+T9a4SJeTl6sfuIfpOf9m4fcWstdz4QQop6Rpl0H2e5LxSVi\nMrb/yaBAa8eUJ6FrxHKatqm4Yf9RxwceruEKhRBCWII07TpElZuL9v13cUhYB8CZZwfxP75b+FPL\nR5jV+lkLVyeEEMLS5Jx2XWA04vD3VegCH8EhYR3lHTtx5ZttvDCggMvOEBP4oUx1CyGEkKZtabZp\nP+E2sB8uEZPBZKIwdh7XUnbxrdcV9p77gSdaDKRbk+6WLlMIIUQdINPjFqK6egXn2A9w+McaVIpC\n6XPD0M+cheLtjcFk4IPUGNQqNTO6vmfpUoUQQtQR0rRrm8mEfcI6tO+/i/ryZQxt26Gf8xHl3Xua\n35KQuY5jVzMZ2X40bXXtLFisEEKIukSadi1Sp/+bggnD8PzlLGX2Gg6+8Qy5IaNo4t6UJsbr2NvY\nU1xezNyDN25XGt4l0tIlCyGEqEOkadcCVWEBTvNicVi1HA+jiY3tYdKAcs64fgVbvrrxHlR4OXnj\nrHHmQtF53n7kHR50bmzhyoUQQtQl0rRrkqJg//VGnKMjsbl4gZMeNkwcZEvI5K9ZaDJwpjCHM/oc\nzhTmcLbwDDn6HE4XnqK5iw8T/CdZunohhBB1jDTtGmJzPAvttCnY7dmNYm/P1hHdebrFj7zeZTI9\nmvaqcDmjyXhjebVNbZUqhBDCSsiffN1vRUU4z3oP9z7dsNuzm+tB/fn35o083e4QOrcmTAqo/Gsy\nbdQ20rCFEELcljTt+0VRsNvyDbqeXXBa/BEm7wfJ/3QdBfEbiDi7jOvG68QEfoBWo7V0pUIIIayU\nTI/fB+qTv6GNCsd+WzKKRkPxW1MomvQOODuz4/R2tv62ma6NA3nmoectXaoQQggrJk37XpSW4hS3\nCKePF6IqLaWsZ2/0cz7C2LoNAGXGMmb8EIFapSa253y5FakQQoh7ItPjd+Fi8UU2Zn1JmbEMzY5t\nuPfuivO8WEyubhSsWEN+4iZzwwZYeXQ5J64dZ3SHEPnmLSGEEPfsjo60Y2NjOXLkCCqVisjISDp1\n6mR+LT4+nk2bNqFWq+nYsSNRUVEYDAaioqI4ffo0RqOR8PBwAgICePnllykuLsbJyQmAiIgIOnbs\nWDPJ7rNyYzkjNw/j8ok0fHe+Q/Dhayg2NhS/HkZx+HQUl0Y3vf9i0QUWHJqDzkHHtC4zLFS1EEKI\n+qTKpn3gwAFOnTpFQkIC2dnZREZGkpCQAIBer2f16tWkpKRga2tLSEgIhw8fJjs7G0dHR7744guO\nHz/O9OnTSUxMBGD27Nm0adOmsh9ZJ8UdnE/w12nM3K3Cuewae33UZEVPYdCTUbed9v5gXwxF5Xpm\nBi7C3UFngYqFEELUN1U27dTUVIKCggDw9fUlPz8fvV6PVqtFo9Gg0WjMR88lJSW4uroydOhQhgwZ\nAoBOp+PatWs1m6KG5Xy7lhHvzKFDLhh17nw/7lmedtrA1TPzeOLbf7OwTxyeTp7m9x84v58vj33B\nww/4MbL9aAtWLoQQoj6p8px2Xl4e7u7u5sc6nY7c3FwA7O3tCQsLIygoiL59++Ln50fLli3RaDTY\n29sDsHbtWnMDB/j4448ZMWIE0dHRlJaW3u8895Xq4kWMI16i8+iJtM+FE889wdXUn2n/1kJ2Dt9H\nz2Z9SD75Lb0TurL9VDJw4+YoUT+EAxDbc778zbUQQoj75q6vHlcUxfxvvV7PihUr2Lp1K1qtltGj\nR5OZmUm7dje+mSo+Pp6MjAyWL18OwKhRo2jbti0+Pj7ExMQQHx9PaGhohT/L3d0JW1sLND2DAZYt\ngxkzoKCAQ40h5Z2niZz8lfktnp7t2BXyHYv2LWL6d9N5afNfGB8wnrYPtOVIbhojO41kSKfg2q+9\nGjw9XSxdQo2SfNavvmeUfNavtjJW2bS9vLzIy8szP7506RKenjemgrOzs2nevDk63Y1ztgEBAaSn\np9OuXTs2bNjAjh07WLp0KRqNBoDg4P82sX79+rFly5ZKf/bVq8V3n+ge2R46gDZ8Mpr0o5S7aJk0\nWMWWPs3Z8cIScnMLb3n/yw+9hr9bV8Zvf5Wlh5YC4KzREu7/7m3fX9d4erpYRZ3VJfmsX33PKPms\n3/3OWNkHgCqnx7t3705y8o2p34yMDLy8vNBqb9zVq2nTpmRnZ5unudPT02nRogU5OTmsX7+euLg4\n8zS5oiiMGTOGgoICAPbv30/r1q3vLdl9pLp8Ge3kibgPCkKTfhT9sBfpGe7F0kcV/hq0DK1dxf+J\nHR94mJTndzO20zhUqIh6LFq+oUsIIcR9V+WRdufOnenQoQMvvvgiKpWKmJgYkpKScHFxITg4mNDQ\nUEaNGoWNjQ3+/v4EBASwcOFCrl27xtixY83rWb16NcOGDWPMmDE4Ojri7e3NxIkTazTcHTGZcIj/\nB84fxqC+ehVD+w4Uzl1IpPFf7D/yK292eZPuTXtWuRoHWwc+7DGX6Y9F46xxroXChRBCNDQq5Y8n\nqeuYmp5SsT16GG3EZDQ/HcLkrKU4IpKS0NfZl3uQp74eSEvXVvw77ChF14w1Wocl1fepK8ln/ep7\nRsln/WpzerxB3sZUlX8N5zkf4vD3VahMJkqffpai92IxNW5CUXkRb+4Yh0ql4uN+y3HSOFFE/f6F\nE0IIYR0aVtNWFOwTE9DOnIE69xKGh1qjn72A8t59zW/5IDWakwW/McF/El0aP2bBYoUQQoibNZym\nXV6O68hh2O38DsXRkaLIaIrHTYT/u1AO4Pszu1iTvpK27u0IfzTSgsUKIYQQt2o4TdtoRH3yN64P\nehL9+7GYfP5008s7T3/HG9tCsFHZEPf4ChxsHSxUqBBCCHF7DadpOzhwdf/hW55WFIW/pf2V2P3v\nY6uy5a994/Dz8rdAgUIIIUTlGk7Tvg19WSETd4xj86+baOzchDUDPuMR70ctXZYQQghxWw22aZ+4\nepwxW18i6+oxApv04JP+n+Ll5GXpsoQQQogKVXlHtPro29820z+xD1lXj/F6p/FsePKf0rCFEELU\neQ3qSNtoMjL/YCwLf5qPo60jy4JW8VybYZYuSwghhLgjDaZpmxQTr2wdwdaTW/Bp1IJPB8TT8YGH\nLV2WEEIIcccaTNMuMZSw/3wqwX96grjHV+DuoLN0SUIIIcRdaTBN21njTPqYE2hsNJYuRQghhKiW\nBnUhmjRsIYQQ1qxBNW0hhBDCmknTFkIIIayENG0hhBDCSkjTFkIIIayENG0hhBDCSkjTFkIIIayE\nNG0hhBDCSkjTFkIIIayENG0hhBDCSkjTFkIIIayENG0hhBDCSqgURVEsXYQQQgghqiZH2kIIIYSV\nkKYthBBCWAlp2kIIIYSVkKYthBBCWAlp2kIIIYSVkKYthBBCWAlbSxdQ22JjYzly5AgqlYrIyEg6\ndepkfi0+Pp5NmzahVqvp2LEjUVFRGAwGoqKiOH36NEajkfDwcAICAnj55ZcpLi7GyckJgIiICDp2\n7GipWDe524xJSUksXrwYHx8fAAIDAxk3bhyZmZnMnDkTgLZt2/Lee+9ZIs4t7jbfsmXL2Lt3LwAm\nk4m8vDySk5Pp168fDz74IDY2NgAsWLAAb29vi2T6o8rybd++nWXLlmFnZ8fgwYMZOXJkhcucP3+e\n8PBwjEYjnp6ezJ8/Hzs7O0vFMqtOvnnz5vHTTz9hMBh4/fXX6d+/P9OmTSMjIwM3NzcAQkND6dOn\njyUi3eJuM+7fv5+33nqL1q1bA9CmTRvefffdejOGGzZsYNOmTeb3pKenk5aWVqf3o1lZWYwfP54x\nY8aYfw9/t3fvXhYuXIiNjQ29evUiLCwMqKXtUGlA9u/fr4wdO1ZRFEU5ceKEMmzYMPNrhYWFSt++\nfZXy8nJFURTllVdeUdLS0pTExEQlJiZGURRFycrKUp577jlFURRl5MiRyrFjx2o3wB2oTsaNGzcq\nc+bMuWVdI0eOVI4cOaIoiqJMnjxZ2bVrVy0kqFx18v1RUlKSsnLlSkVRFKVv376KXq+vpcrvTGX5\njEaj0qtXL+Xy5cuK0WhUQkJClPPnz1e4zLRp05QtW7YoiqIoH330kRIfH1/LaW5VnXypqanKq6++\nqiiKoly5ckXp3bu3oiiKEhERoezYsaPWM1SlOhn37dunTJw48ZZ11Zcx/P/Lz5w5U1GUursfLSoq\nUkaOHKnMmDFD+eyzz255feDAgcq5c+cUo9GoDB8+XDl+/HitbYcNano8NTWVoKAgAHx9fcnPz0ev\n1wOg0WjQaDQUFxdjMBgoKSnB1dWVoUOHMn36dAB0Oh3Xrl2zWP13ojoZb6esrIyzZ8+aP0H37duX\n1NTU2glRiXvJZzAY+OKLL2751FyXVJbv6tWrNGrUCJ1Oh1qtpmvXruzdu7fCZfbv38/jjz8OWMf4\nVZTv0UcfZfHixQA0atSIkpISjEajxTJUpToZK1JfxvCPlixZwvjx42u97rthZ2fHypUr8fLyuuW1\nnJwcXF1dady4MWq1mt69e5Oamlpr22GDatp5eXm4u7ubH+t0OnJzcwGwt7cnLCyMoKAg+vbti5+f\nHy1btkSj0WBvbw/A2rVrGTJkiHn5jz/+mBEjRhAdHU1paWnthqlAdTICHDhwgNDQUEaPHs0vv/xi\n3vh+5+HhYV6PJVU3H0BKSgo9evTAwcHB/FxMTAzDhw9nwYIFKHXg5oCV5dPpdBQVFXHy5EnKy8vZ\nv38/eXl5FS5TUlJinoazhvGrKJ+NjY15+jQxMZFevXqZT2l8/vnnjBo1irfffpsrV67UfqDbqE5G\ngBMnTvDGG28wfPhwfvzxR4B6M4a/O3r0KI0bN8bT09P8XF3cj9ra2t60n/ij3NxcdDqd+fHv+Wtr\nO2xw57T/6I87ab1ez4oVK9i6dStarZbRo0eTmZlJu3btgBvnSjMyMli+fDkAo0aNom3btvj4+BAT\nE0N8fDyhoaEWyVGZO8no5+eHTqejT58+pKWlERERwapVqypcT11yN2O4cePGm87Lv/nmm/Ts2RNX\nV1fCwsJITk5mwIABtZ6hMn/Mp1KpmDNnDpGRkbi4uNCsWbMql6nsubrgbvJt376dxMRE1qxZA8BT\nTz2Fm5sb7du355NPPiEuLo7o6Oharf9O3EnGFi1aMGHCBAYOHEhOTg6jRo0iJSWlwvXUJXczhomJ\niTzzzDPmx9ayH62OmtoOG9SRtpeX102f+i5dumT+xJednU3z5s3R6XTY2dkREBBAeno6ABs2bGDH\njh0sXboUjUYDQHBwsPnCrX79+pGVlVXLaW6vOhl9fX3NF/D4+/tz5coV3N3dbzoVcPHixdtOFdW2\n6o5hcXExFy5cuGkn8vTTT+Ph4YGtrS29evWqE2NYWT6ALl26sG7dOlasWIGLiwtNmzatcBknJyfz\nkYs1jB/cPh/Anj17WL58OStXrsTFxQWAbt260b59e8B6tkG4fUZvb28GDRqESqXCx8eHBx54gIsX\nL9arMYQb0/3+/v7mx3V1P1qZ/5//93Gpre2wQTXt7t27k5ycDEBGRgZeXl5otVoAmjZtSnZ2tvk/\nNz09nRYtWpCTk8P69euJi4szT5MrisKYMWMoKCgAbvwi/n7Vp6VVJ+PKlSv55ptvgBtXTP7e9Fq1\nasWhQ4eAG1PLPXv2tECim1UnH0BmZiatWrUyr6ewsJDQ0FDKysoAOHjwYJ0Yw8ryAbz66qtcvnyZ\n4uJidu7cSbdu3SpcJjAw0Py8NYwf3D5fYWEh8+bNY8WKFeYrxQEmTpxITk4OYD3bINw+46ZNm1i9\nejVwY/r18uXLeHt715sxhBsNy9nZ2TxVXJf3o5Vp1qwZer2eM2fOYDAY2LlzJ927d6+17bDBfcvX\nggULOHToECqVipiYGH755RdcXFwIDg5m/fr1JCUlYWNjg7+/P+Hh4SxcuJDNmzfTpEkT8zpWr17N\n9u3bWbVqFY6Ojnh7ezNr1iwcHR0tmOy/7jbjhQsXmDp1KoqiYDAYzH+qcOLECaKjozGZTPj5+Zkv\nyLO0u80HkJyczN69e2+aHl+7di1ff/019vb2/PnPf+bdd99FpVJZKpZZZflSUlJYsmQJKpWKkJAQ\nhg4dettl2rVrx6VLl4iIiOD69es0adKE2bNnm2eKLOlu8yUkJPC3v/3tpusT5s6dy+nTp5k/fz6O\njo44OTkxe/ZsPDw8LJjsv+42o16v55133qGgoIDy8nImTJhA7969680Ywo0P0YsWLbrp1NuWLVvq\n5H40PT2duXPncvbsWWxtbfH29qZfv340a9aM4OBgDh48yIIFCwDo37+/eUq/NrbDBte0hRBCCGvV\noKbHhRBCCGsmTVsIIYSwEtK0hRBCCCshTVsIIYSwEtK0hRBCCCshTVsIIYSwEtK0hRBCCCshTVsI\nIYSwEv8LMFc1Az8t0JYAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jgmH3wwt1src",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Okay, so we are doing good!
\n",
+ "\n",
+ "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
+ "\n",
+ "Or better, do it yourself!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OZ5TY7B_4E_v",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "def linear_regression(learning_rate, n_epochs, interval):\n",
+ " x = tf.placeholder(tf.float32, name='x')\n",
+ " y = tf.placeholder(tf.float32, name='y')\n",
+ " W = tf.Variable(0.0, name='weight_1')\n",
+ " b = tf.Variable(0.0, name='bias_1')\n",
+ " pred_y = (W*x) + b\n",
+ " loss = tf.reduce_mean(tf.square(y - pred_y))\n",
+ " optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)\n",
+ " with tf.Session() as sess: \n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X[:10], test_Y[:10], 'g', label='True Function')\n",
+ " plt.plot(test_X[:10], final_preds[:10], 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()\n",
+ " pass"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "A6MaclhK4rc6",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 567
+ },
+ "outputId": "e82d8e90-201e-4325-a440-cd3984ebcf3b"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Okay! Now let's tweak!\n",
+ "linear_regression(learning_rate=0.000034, n_epochs=500,interval=50)"
+ ],
+ "execution_count": 24,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.1925572\n",
+ "Loss after epoch 50 is 0.1914878\n",
+ "Loss after epoch 100 is 0.19042648\n",
+ "Loss after epoch 150 is 0.18937314\n",
+ "Loss after epoch 200 is 0.18832773\n",
+ "Loss after epoch 250 is 0.18729019\n",
+ "Loss after epoch 300 is 0.18626046\n",
+ "Loss after epoch 350 is 0.18523851\n",
+ "Loss after epoch 400 is 0.18422425\n",
+ "Loss after epoch 450 is 0.18321761\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.7947332\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3Xt8VPWd//H3mZlkQsgkZMIMyk0w\n3EpYEJb9uUorYsNu1+o+uruu0tpilZZFwS5WBAlqsEtStmvZquiv6FLLo/ITqKat3bpg65bt2gap\nBWNJCxRUULkkITdCmJnM5Pz+yGSSQMiNJN9k5vX0kcec63e+nzmYd85lzrFs27YFAAD6ncN0BwAA\nSFSEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhrj6+w3Ly8/2afuZmamqqqrv0/cYaKg5cSRi3dSc\nGOK9Zp/P0+70uNsTdrmcprvQ76g5cSRi3dScGBKxZikOQxgAgMGCEAYAwBBCGAAAQwhhAAAMIYQB\nADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwJB+v3c0AAB9ybZtBSNBBSMBBSMhBSMBhSJBBcJB\nhSLB6Lzm+dHhcFDBxqbX4UOG67ZJd8iyrD7vKyEMAOhVtm3rfPi8zoZqda6hToFIU/g1vwbDgZbh\n6E9SilRZW6tAOKBQNDhblomGaTigYGPTa/O6gUjL8s3LhBpDl13DvLG5Gj5keC98Gh0jhAEAMa0D\ntDZUq9pQjWqDta3Gm6adDbaMx+YFa5qWD9Uq3Bjusz46LIdSnClKdibL7UyR2+lWpturZKdbKS63\n3NF5Tcu45W7+cbmV7Gi9jFspTvcFy6RodNrofglgiRAGEGds29a5hjqdCZxRVaBSlYFKVUV/mqdV\nBSoVjITkdiYrOfZLOFlJjmS5nW4lR6e7Y69uJTmSovPc0V/+La9N67Vtq3k9h9V/l97Ytq1AJBAN\nw+4HaPNwQ2NDt9871ZUqT3K6slKGa3xGttKT05WenKGhSUOV4moOvGhwulIuCj+/N1OBuojcrpQL\ngrJVmLrccjvccjlc/XKouD8QwgAGrEhjRBX1FTpSdbxNgMaCNVipM+fPqCrYdnpPQqSvOC3nBcEe\nHXY0T7sg+B1upQ8dqsYGq820ZGeyGtXYRwE6VOnudGUNGa5xGVfHAjTdnS5Pcnp0PDrszrhgPF2e\npHQlOZMu63Py+Tx9/rz5gYgQBtAvAuFAS1BGQ/PM+ejearCyVcCeiYVpTbBGtuxO27ZkKcOdIW9K\nlsZ4xsqb4lVm9Mfr9so7JKtlmtsrb4pXbpc7ei4xqFAkFP0JKtjY9Np0zrF5OKRQdHrztGAkqIZI\ng4KNwdgyLW0Fo8u3ndY8fDZ0VqFIRWx+xI70+HMdCAGKniOEgX4WioRUHaxWdaBKVcEqVQerVB1o\neq0KVikcCcuyLFmy5LAsKTpsyZInbYjq60OxcYfliB6Ws2RZlhxyxNa1LF0wbsmyHLF1W97D0Wb8\nwtfm92j3PaPj9eFzsYCtjB0GrmoTrPXh+i59PkmOJGWmeHXF0Cv1iawcXZHuV5ojQ5nuaKg2h2tK\nS7AOcw+T0zF4HwofaYxEAzqoUGODPMOSdLLsTKvADynUGJQlqylEo2HqSU6Xy8Gv8cGMrQf0QPN5\nx6pYgFY3hWg0TNuE7AXz68PnTHe/36S6hsqb4tWEzEnKdGe22UPNSslq2VttNW1oUlqb832JcJjS\n6XAq1ZGq1KRUSZIvw6MhoUzDvUJ/IIQTWCAcUE3sIo0a1UTPK9VEL+aoDVVHzzfV6mzDWTnkkDt6\nUUXzhRPNF6m0XIWYfNHFFC3DydGLMKLzXSmxc14pzhQjf9GHG8OqDlarplWAVgWqVBOsjgVoVTA6\nHgvYplDtztWfnuR0ZbozNSFzojLcw5TpztQwd6YyUzJbxlMyNcw9TEmOZNnR/2TbarQbY+MZGUNU\nWVXXNGZHpzbPj443xqa3fm1sM9544Xi0DUltxi+cH2uv1Xs2qlFDXKnyRvdOW4eq2+nuq00HxAVC\neJCKNEZigflxJKJjp05Gw7PlKwI1rS7WaBpuCtrmCzl647t0vclhOWJXSra+arL11wiahz2pQ2WH\nHW2utmy+eKV1uNc31LcN0miwNg+fDdV2uX8uh0vDouE5Lv1qZaZkRseHaVhKZpsgbQ7YYW6vMtwZ\nvfYHhs/nUXlafO8VAomEEDbAtm3Vh+ubAjJYq5pQdVOgBtuGZ02wOnYFZMu0pmXqGrr/izjFmSJP\ncrqGuYdprGesPMnpynAPa3OOKcOd0Wa6p3lakkeNalQoEmr5Mn1jMPql+VDsC/ehNl+eb5nWdrid\nO9i0+QJ+8/ymc6fNF7UEIoFe+fxTXUOVmZKpsZ6rOgnQtgF74WFSALhcCR3CkcaIApGAAuFA9O4s\nAQXDQQXC52N3YonNCzfd3iwQPq9A8x1cwkEFIucVCAdbLRNtp3nZcMut0ZrXDYTPd/tqSIfliF31\neFX6OGU0X+XoztCIjOFKahyi9OQMZUSvikxPbp6frvTkYUp3pw/6Q4O2bauhsUGhSFBpw5J0ouxM\n2/APBxVqDLYJ9yFJqU2h2ipkk53JpksBAEmDPITPhmr1/LvfVVWgUuejAShXRDX1dbEgbb49Wmw8\nEogt25d3dJGa9jzdrqa7uaS4hihryPDY3V2awrElIDOSM+SJTmsajgZqdE+0o72wRLhwRZIsy4p9\nr9I31COlpZjuEgBclkEdwm+f+q3W713X4TLNAeiOXvyT6fbqyqHRcVdK26B0pijFlSK3MyV2t5bW\n6148L7q+M0VuV9P7pEQvPHI73Ry6BAB0qEshXFhYqJKSElmWpby8PE2fPj02b+vWrXr11VflcDg0\nbdo0rVmzps86e6Ebx9yk3XcUK9zYoBTnELldbo3yD9e5mnDsCtz+vGUcAADd0WkI7927V8eOHdP2\n7dt19OhR5eXlafv27ZKkuro6bd68Wa+//rpcLpfuuecevfPOO7rmmmv6vONS0+HJqVk5bab5PB6V\nB+L/0CwAYPDrdDexuLhYubm5kqTs7GzV1NSorq5OkpSUlKSkpCTV19crHA7r/PnzysjI6NseAwAQ\nJzoN4YqKCmVmtty5xev1qry8XJLkdru1dOlS5ebmat68eZoxY4bGjx/fd70FACCOdPvCLNtuuZl6\nXV2dNm3apJ07dyotLU133XWXDh48qClTplxy/czMVLlcfXuPV5/P06ftD0TUnDgSsW5qTgyJWHOn\nIez3+1VRUREbLysrk8/nkyQdPXpUY8aMkdfrlSTNnj1bBw4c6DCEq6q6dhP3nkqUr+u0Rs2JIxHr\npubEEO81X+oPjE4PR8+ZM0e7du2SJJWWlsrv9ystLU2SNGrUKB09elSBQNOdjA4cOKBx48b1UpcB\nAIhvne4Jz5o1Szk5OVqwYIEsy1J+fr6Kiork8Xg0f/58LVq0SAsXLpTT6dTMmTM1e/bs/ug3AACD\nnmW3PsnbD/r6cEO8H9JoDzUnjkSsm5oTQ7zX3OPD0QAAoG8QwgAAGEIIAwBgCCEMAIAhhDAAAIYQ\nwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAh\nhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBg\nCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAA\nGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAA\nAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIa4urJQYWGhSkpKZFmW\n8vLyNH369Ni8kydP6utf/7oaGho0depUfeMb3+izzgIAEE863RPeu3evjh07pu3bt6ugoEAFBQVt\n5q9fv1733HOPXn75ZTmdTp04caLPOgsAQDzpNISLi4uVm5srScrOzlZNTY3q6uokSY2Njfrd736n\nm266SZKUn5+vkSNH9mF3AQCIH50ejq6oqFBOTk5s3Ov1qry8XGlpaaqsrNTQoUP1zW9+U6WlpZo9\ne7YefPDBDtvLzEyVy+W8/J53wOfz9Gn7AxE1J45ErJuaE0Mi1tylc8Kt2bbdZvj06dNauHChRo0a\npcWLF2v37t268cYbL7l+VVV9jzraVT6fR+XlZ/v0PQYaak4ciVg3NSeGeK/5Un9gdHo42u/3q6Ki\nIjZeVlYmn88nScrMzNTIkSM1duxYOZ1OXXfddfrTn/7US10GACC+dRrCc+bM0a5duyRJpaWl8vv9\nSktLkyS5XC6NGTNGH3zwQWz++PHj+663AADEkU4PR8+aNUs5OTlasGCBLMtSfn6+ioqK5PF4NH/+\nfOXl5enhhx+WbduaNGlS7CItAADQsS6dE16xYkWb8SlTpsSGr7rqKr300ku92ysAABIAd8wCAMAQ\nQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAw\nhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAA\nDCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgA\nAEMIYQAADCGEAQAwxGW6AwCA/vX00/+uQ4f+qMrKMwoEAho5cpTS0zNUWPhvvdL+bbfdKr9/hByO\nlv28jRufu+x233zzf3TttdertrZGmzdv0sqVay67TdMIYQBIMPff/4Ak6bXXfqr33juqZcuW9/p7\nPPHEU0pNTe3VNrdt26pZs/5CWVnD4yKAJUIYABC1b9/b2rbtRdXX12vZsgf04IPL9LOfvSFJeuSR\nlfr7v79dU6Z8QoWFj+vs2bOKRCJavvwhTZgwsUvtf/azn76ovf37f6dz5+p06tTHev/9D/S1rz2o\n666bo507f6aXX94uy7K0YMGdamho0B/+cEArVnxNDz/8qB5//BFt3vwD7dv3tp577lm5XC75fH6t\nXv2YfvGLXXr33XdUXV2l48eP6Qtf+JJuueVzffa5XQ5CGAAMWvubR/TToz9uM83hsNTYaPe4zVuz\nP6e116/r0bpHjx7RSy8VKTk5ud35O3a8pGuvvV633vo5vf/+e3ryySf0ne882+O+SlJZ2Wk9//zz\n+ulPd+knP3lFM2Zco+9//z+0ZctLCoUaVFCQr/XrN+g//uO7euKJp1RTUx1b94knvql///dnNGLE\nFdqw4V/185/vlGVZOnr0iL773e/po48+VH5+HiEMABj4JkyYeMkAlqTf//5dVVdXadeu1yRJwWCg\n3eVWrPha7JzwsGGZWrfuXy/Z5vTp10iS/H6/6urq9MEH72vs2HFyu1Pkdqdo/foN7a5XW1sjy7I0\nYsQVkqRZs2brnXf2adKkKZo2bbqcTqd8Pr/OnavrvHBDCGEAMGjt9esu2mv1+TwqLz9rpD9JSUnt\nTg+Hw9H5Lj3wwEOaNm16h+10dk64uT1JcjqdsWHbtuVwOGXbjV3orSXbbjli0NDQIMtytNvmQMVX\nlAAA7bIsS4FAQIFAQIcPH5IkTZ06Tb/61W5J0vvvv6dt2168rPbac9VV43T8+DHV19crGAxq+fL7\nZNu2LMuhSCQSWy49PV2WZenUqVOSpHfe2acpUz7Rg0rNYU8YANCuz33uNi1efJfGjbtakyc3hdtt\nt92hgoK1uu++r6ixsVHLl6+4rPbaM2TIEC1atETLl98nSbrjji/IsizNnDlL9923SGvWrI0tu3Ll\nI3r88TVyOp0aNWq0Pv3pv9Lrr/9Xzwo2wLL7eT+9rw+xmDyMYwo1J45ErJuaE0O81+zzedqdzuFo\nAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCE7wkDQII5efKEFi5coMmTp0iSQqGQ7rzzLs2d\nO6/bbb3yynZVV1frhhtu1K9+tVuLFv1Tu8s1P4bwUnfkau29945ow4ZvXfT4w7lzr9Wf/dmM2HhW\nVpYef/yb3e7zhX75y19o3rxc/elPhzqsoS8QwgCQgMaOvSoWcrW1Nbr77jv1l395ndzulB61N3Hi\nZE2cOPmS85sfQ9iVEL6UtLS0Xnku8YVefHGL5s3L7bSGvkAIA0CCS0/PUFbWcJ05c0YvvPC8XK4k\n1dZW6xvfWK9vfatAJ058rHA4rK98ZYn+/M//Qm+/vVdPPfVteb1ZysoarpEjR2nfvrdVVLRD69Z9\nq8PHED755P/Vq6/+SL/4xU5ZlkOf+tSN+vznv6hTp07pvvuWKSkpSRMmTOpy30+ePKFHHlmlzZt/\nIElatOhLWrfuX/W97z2n4cN9OnTojzp9+pQee2ydJk+eoq1bt2j37jdkWQ4tWbJMBw/+QUeOHFZe\n3kO67bY7YjW88cbPtX37VjmdTk2e/AktX75Cmzdv0rlzdTp+/Jg+/vij2GMXLwchDAAGDV37iNw/\nbfsoQzkseS/jUYbBWz+nc2u7/ijDkydPqLa2Rn7/CElN92RetWqNdu78mbKyhmv16sdUXV2tf/7n\nJdqyZZs2bdqoRx/9F02cOEkrVnxNI0eOirVVX3+uw8cQlpeXaffuN/Tss5slSffeu0jz5uXqv/7r\nR/r0p/9Kt9/+eb344vd15MjhHtffLBQKacOGjfrxj1/Wzp0/U2pqqnbvfkObNn1fJ058rBdf/L4e\nfvhRbd26RYWF/6Z9+96O1lCv5557Ri+88P+UmpqqlSsfiM0rKzutJ554Snv2/EY/+ckrhDAAoPuO\nHz+mZcsWS5KSk5P1yCOPy+VqioSpU3MkSQcOvKuSkv169913JEnBYFANDQ06efKkJk5s2lu95ppZ\nCgaDsXY7ewzhH/9Yqo8++lD339903rW+/pxOnTqho0eP6s4775YkzZw5W3v2/OaiPtfV1cX6LEnZ\n2RO0YMEXL1njjBkzJUk+3wj94Q+lOnz4kKZOnSaHw6HRo8fo4YcfbXe9Dz88rtGjx8aeAjVz5p/r\n8OGDki5+7OLl6lIIFxYWqqSkRJZlKS8vT9OnX/wIq29/+9t655139IMf/OCyOwUAieLc2nUX7bX6\nfB5V9vF9lFufE76Qy5UUe1248B7Nn/+ZNvObnxMsXfyYwM4eQ+hyJem66+Zo5co1bab/8IdbY48h\nvNT67Z0TPnXqZJvxjh6R6HQ61NiFIwyW1baucLhBbre73TYvV6dfUdq7d6+OHTum7du3q6CgQAUF\nBRctc+TIEf32t7+97M4AAAaOqVOn6c03/0eSVFVVqU2bnpEkDR/u0/HjH8i2be3f/7s263T2GMLJ\nkz+hfft+p0AgINu29Z3vPKFgMKDx48fr4ME/SFLs0G9XpKYOVVVVpWzb1pkzFTpx4qNLLjt58if0\n+9+XKBwOq7LyjFavbnoC1IXBPGbMVfroo+Oqrz8nSdq/f58mT57a5T51R6d7wsXFxcrNzZUkZWdn\nq6amRnV1dUpLS4sts379ej3wwAPauHFjn3QSAND/bropV/v2/VZLltyjSCSie+5pOhS8ePF9euSR\nVbriiitj55GbdfYYwqeffk633/55LV36VTkcDt1ww41yu1O0cOFCLV16v371q18qO3til/uYnp6u\n2bP/j77ylYWaMGFih1c3X3nlSP31X9+sZcsWy7Zt/dM/LZUkTZo0WV/96kLde+/XYjUsXfrPevDB\n+2VZDk2ffo1mzLhGb7/9Vrc+v67o9FGGjz76qObOnRsL4i984QsqKCjQ+PHjJUlFRUWqqKjQzTff\nrNWrV3d6ODocjsjlcna4DAAAiaDbF2a1zuzq6moVFRXphRde0OnTp7u0flVVfXffslvi/ZmU7aHm\nxJGIdVNzYoj3mnv8PGG/36+KiorYeFlZmXw+nyRpz549qqys1J133qlly5aptLRUhYWFvdRlAADi\nW6chPGfOHO3atUuSVFpaKr/fHzsf/JnPfEavvfaaduzYoY0bNyonJ0d5eXl922MAAOJEp4ejZ82a\npZycHC1YsECWZSk/P19FRUXyeDyaP39+f/QRAIC41KVzwitWrGgzPmXKlIuWGT16NN8RBgCgG3iU\nIQAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAI\nIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY\nQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAA\nhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwA\ngCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggD\nAGAIIQwAgCGurixUWFiokpISWZalvLw8TZ8+PTZvz5492rBhgxwOh8aPH6+CggI5HGQ7AACd6TQt\n9+7dq2PHjmn79u0qKChQQUFBm/mPPfaYnnrqKW3btk3nzp3T//7v//ZZZwEAiCedhnBxcbFyc3Ml\nSdnZ2aqpqVFdXV1sflFRka644gpJktfrVVVVVR91FQCA+NJpCFdUVCgzMzM27vV6VV5eHhtPS0uT\nJJWVlenXv/615s6d2wfdBAAg/nTpnHBrtm1fNO3MmTNasmSJ8vPz2wR2ezIzU+VyObv7tt3i83n6\ntP2BiJoTRyLWTc2JIRFr7jSE/X6/KioqYuNlZWXy+Xyx8bq6On31q1/V8uXL9clPfrLTN6yqqu9h\nV7vG5/OovPxsn77HQEPNiSMR66bmxBDvNV/qD4xOD0fPmTNHu3btkiSVlpbK7/fHDkFL0vr163XX\nXXfphhtu6KWuAgCQGDrdE541a5ZycnK0YMECWZal/Px8FRUVyePx6JOf/KR+/OMf69ixY3r55Zcl\nSbfccovuuOOOPu84AACDXZfOCa9YsaLN+JQpU2LDBw4c6N0eAQCQILirBgAAhhDCAAAYQggDAGAI\nIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY\nQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAA\nhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwA\ngCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggD\nAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhrhMd+ByWKdPa2jh43LU1bVMdLuUHgz3\nzhvYdu+009fttq55sPT5ctvu0nYeYH3ujXaTXUoP9fDf92D9t3E5NXfAGsifR7JLGe3VPJD7fMm2\nu7hcslMZoUg32u27PjdecYXOfucZKSmpz96j2aAOYef77yllx0uyIm03nNtQf0yi5sSRiHUnYs3J\npjtgwECpudHnl3WuTvawzD5/L8u2+/JPoIuVl5/t1fass7VSMBQbHz48TRUVdR2s0d03sHqvrTbt\n9l5Tw4d7VFHR6nPtsz73Ubs9aPuimnup3W4x8Dl3ue5LsHvzH15rffg5+/zpvf57I2aA/r/i83ku\nXfMA7fPltt1hzZfRbo84HE0/vcjn87Q7vUt7woWFhSopKZFlWcrLy9P06dNj837zm99ow4YNcjqd\nuuGGG7R06dLe6XEX2Z50qXVtPo9spfRrH4zL8shuHCh/Q/aTYR7ZDU7Tveh/Ho/sgOlO9LPUVCm1\nG4cp40FKipTSYLoX/SspqV8O/w40nUb93r17dezYMW3fvl0FBQUqKChoM3/dunV6+umn9dJLL+nX\nv/61jhw50medBQAgnnQawsXFxcrNzZUkZWdnq6amRnXRC6E+/PBDZWRk6Morr5TD4dDcuXNVXFzc\ntz0GACBOdBrCFRUVysxsOTnt9XpVXl4uSSovL5fX6213HgAA6Fi3r46+3Ou4MjNT5XL17bm8S50A\nj2fUnDgSsW5qTgyJWHOnIez3+1VRUREbLysrk8/na3fe6dOn5ff7O2yvqqq+p33tkh5dYTfIUXPi\nSMS6qTkxxHvNl/oDo9PD0XPmzNGuXbskSaWlpfL7/UpLS5MkjR49WnV1dfroo48UDof1y1/+UnPm\nzOnFbgMAEL863ROeNWuWcnJytGDBAlmWpfz8fBUVFcnj8Wj+/Plau3atHnzwQUnSzTffrPHjx/d5\npwEAiAeD/mYdF4r3QxrtoebEkYh1U3NiiPeae3w4GgAA9A1CGAAAQwhhAAAM6fdzwgAAoAl7wgAA\nGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgSLcfZWhCYWGhSkpKZFmW8vLyNH369Ni8rVu36tVX\nX5XD4dC0adO0Zs0ahcNhrVmzRsePH1ckEtHKlSs1e/ZsHTx4UGvXrpUkTZ48WY8//rihijrXWzV/\n6UtfUn19vVJTUyVJq1at0rRp00yV1aHu1nzmzBmtWrVKwWBQDQ0NWr16tWbMmBHX2/lSNQ+m7Sx1\nv+5mFRUV+pu/+Rtt3LhR1157bVxv62YX1jyYtnV3ay4qKtKTTz6psWPHSpKuv/563XvvvYNqO3eb\nPcC99dZb9uLFi23btu0jR47Yt99+e2ze2bNn7Xnz5tkNDQ22bdv23Xffbe/fv99++eWX7fz8fNu2\nbfvw4cP2P/zDP9i2bdtf/OIX7ZKSEtu2bfvrX/+6vXv37n6spOt6u+ZDhw71bwE90JOav/e979mv\nvvpqbP27777btu343s4d1TwYtrNt96zuZg899JD9d3/3d/aePXts247vbd2svZoHw7buSc2vvPKK\nvX79+ovaGizbuScG/OHo4uLaSIFHAAAESklEQVRi5ebmSpKys7NVU1Ojuro6SVJSUpKSkpJUX1+v\ncDis8+fPKyMjQ3/7t3+r1atXS5K8Xq+qq6sVCoX08ccfx/4SmzdvnoqLi80U1Yneqnkw6UnNd999\nt2699VZJ0smTJzVixIi4387t1TzY9KTu5vWGDh2qSZMmSVLcb+vm9VrXPJj0tOYLDabt3BMD/nB0\nRUWFcnJyYuNer1fl5eVKS0uT2+3W0qVLlZubK7fbrc9+9rMXPUpxy5YtuuWWW1RVVaX09PTY9Kys\nLJWXl/dbHd3RWzU3e+qpp1RVVaXs7Gzl5eUpJSWl32rpqp7WXF5eriVLlujcuXPasmVLQmznC2tu\nNhi2s9SzukOhkJ555hk9++yzKiwslKS439bt1dxsMGzrntS8f/9+7d27V4sWLVI4HNaqVauUlZU1\naLZzTwz4PeEL2a3usllXV6dNmzZp586deuONN1RSUqKDBw/G5m/dulWlpaVaunRph+0MdJdT88KF\nC7Vy5Upt3bpVlmVp69at/d7/nuhqzT6fT6+88opWr14dOxJwqXYGusupebBuZ6lrdT/33HP6x3/8\nxza/jDtqZ6C7nJoH67buSs0zZszQ/fffr82bN2v58uVatWpVh+3EgwG/J+z3+1VRUREbLysrk8/n\nkyQdPXpUY8aMkdfrlSTNnj1bBw4c0JQpU/TDH/5Q//3f/61nn31WSUlJFx2iPX36tPx+f/8W00W9\nVbMkzZ8/P9bOTTfdpNdee60fK+m6ntRcW1uryZMnKyMjQ3PnztXKlSvjfju3V7M0eLaz1LO633zz\nTTU2Nmrr1q06fvy43n33XW3YsCGut3V7NT/55JODZlv3pObbbrtN2dnZkqSZM2eqsrJSmZmZg2Y7\n98SA3xOeM2eOdu3aJUkqLS2V3+9XWlqaJGnUqFE6evSoAoGAJOnAgQMaN26cPvzwQ23btk0bN26U\n2+2W1HQO4uqrr9bbb78tSXr99df1qU99ykBFneutmm3b1pe//GXV1tZKkt566y1NnDjRQEWd60nN\nr7/+un70ox9Jkg4dOqQrr7wy7rdzezUPpu0s9azubdu2aceOHdqxY4duvPFG5efna8qUKXG9rdur\necKECYNmW/ek5ueff17/+Z//KUk6fPiwvF6vkpOTB8127okBvyc8a9Ys5eTkaMGCBbIsS/n5+Soq\nKpLH49H8+fO1aNEiLVy4UE6nUzNnztTs2bNjfyEvXrw41s7mzZuVl5enxx57TI2NjZoxY4auv/56\ng5VdWm/WfPvtt+vLX/6yhgwZohEjRuj+++83WNml9aTmq6++Wg8//LB+/vOfKxQKxb7CEM/bub2a\nLcsaNNtZ6lndlxLP27o9g2lb96Tm0aNH66GHHtK2bdsUDodVUFAgafBs557gUYYAABgy4A9HAwAQ\nrwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwJD/D527z7x7UUU5AAAAAElFTkSu\nQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "peoHmV2M40uU",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 751
+ },
+ "outputId": "1d10a76a-20d4-4020-e175-300431edad5b"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0000006, n_epochs=1000,interval=50)"
+ ],
+ "execution_count": 25,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.1925572\n",
+ "Loss after epoch 50 is 0.19253828\n",
+ "Loss after epoch 100 is 0.19251934\n",
+ "Loss after epoch 150 is 0.1925004\n",
+ "Loss after epoch 200 is 0.19248146\n",
+ "Loss after epoch 250 is 0.19246252\n",
+ "Loss after epoch 300 is 0.1924436\n",
+ "Loss after epoch 350 is 0.19242467\n",
+ "Loss after epoch 400 is 0.19240576\n",
+ "Loss after epoch 450 is 0.19238684\n",
+ "Loss after epoch 500 is 0.19236791\n",
+ "Loss after epoch 550 is 0.19234902\n",
+ "Loss after epoch 600 is 0.19233009\n",
+ "Loss after epoch 650 is 0.19231117\n",
+ "Loss after epoch 700 is 0.19229227\n",
+ "Loss after epoch 750 is 0.19227336\n",
+ "Loss after epoch 800 is 0.19225445\n",
+ "Loss after epoch 850 is 0.19223554\n",
+ "Loss after epoch 900 is 0.19221666\n",
+ "Loss after epoch 950 is 0.19219775\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.8250578\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3Xt8VPWd//H3mZnMJCGTy8AE5aYY\nbmtYEMrWKt6oYR+7W921LZVYLUrZUhRt0SJIsAb8kZTtKrsq+qtatDxqfoDVtLVrC1Zbtrcga9G4\npBVKtNwvCeQeMpPJnN8fkwwJJORCwjfJvJ48eMy5fs/3k/N45J1zmXMs27ZtAQCAi85hugMAAMQq\nQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAENcF3uDZWU1fdp+WlqiKirq+3Qb/Q01x45YrJuaY8Ng\nr9nv97Y7fdAdCbtcTtNduOioOXbEYt3UHBtisWZpEIYwAAADBSEMAIAhhDAAAIYQwgAAGEIIAwBg\nCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhF/3Z0QAA9KWmcJMCTQEFmhoUbAqqofmzzbRQg4Lh\noIJNgchwq+WGJQzTnAlzZVlWn/eVEAYA9KqmcJNqgtWqDlarrrFOgaYGBZoigdcyHGgdjKEGxSVY\nOllVdW5YNn8GmwKtwrS5jVCDAs1BGgidabfJbrrgGmaNydKwhGG98NM4P0IYABAVaAqoOlCtmmCV\naoI1qm4O05pgtaoDVapprGme32p6q8/qQLXqQ3V92ke3wy230yOP0y2PM17xznilelLldnrkdrgV\n74qXu3leyzKtlz9nmiu+1XoejUoadVECWCKEAQwitm2rLlSnyoYKVTSc0qmGU5HPQOSzsqEiOi0Q\nDsrT/Mvc7Yxr/oXsUZzjzLDb6Y7+wo/8Uo/Mj8w7s57b6ZHH4VZc8zJnlnXL44ysH+eI69PTmy21\n1wSqm8Oz6qyQjEyrCZwZjwZnsEo1zdMCTYFub9vlcCnZnSyvO1kZqePkdXuj40PihsjjigRl62B0\nOz1tpqX7UtVQF47+LD2u9gPU7XTLYQ2e25kIYQD9UmNToyoCFSorO6jSIwdVEWgbrC3DlWdND4aD\nprveodZHcHHNQXQmvN3RQE+KT5CanGemOdxyO90K2+GzwrO6OTwjAdqT07AJrgR53clK8aRqtHeM\nvO4UJbuTm0PUK687WcmeZCW7U+RtnhaZnyKvJ1neOK8SXAkX/AeG3+/t8/fN90eEMIA+Zdu2qoNV\nqmg+Oq0ItA7SClUETrUK0ZZlKlQTrO7yNlI8qUrzpGnksL9Vanya0jw++eJ9Sov+bzvNF++T2+lR\nsCnQfHNO5DpkY1OjAk2ByDXGcFCN0euYQTWGg83zmpdttV7kmmVQwXCr4eb1IttojHy2Gm5Zr76x\nttX10u4dhXrdkRC8ZMilGp82MRqeSc2fyc0BmhTnVbKndbgmRwPV7XR3d5eiFxHCwEUSCodUFahS\nVaBCFYEKVQUqVdFQocpAZWS4eVpjU6Msy5IlSw7LER22ZCkhwa1goElqmWJZclhnhlv+OSyHdNZ4\n6/mt11PrbbXTTuQIp3kdtWrHUnSZ+sb6SIgG2p7yjQRsRZeP0BJcCUr1pGm0d0w0MEekDle8nRQN\nz7R4n9I8zcEa71OqJ1UuR89+lfW3ALJtW6FwSMk+tw4fL2/1R0Ek7C3LahW03kF1WjZWEcJAN9i2\nrZpgdTQwKwOVqmwO0sj/M+Fa1WpaZaCyW0d2A53DcijNEwnJsSkZ0eHWQeqL9ym1eXrLtARXwjlt\nxdJpSsuyFOeMU5I7Sb5423R3cBEQwjEmFA6pOlilqkBVm7sZW27MqApUnXWn45kbNhyWI3rDSuub\nTzzRmyuab2RpdcNF2zsSW8/3tL35pc1NGp5WN3B45HQ4e/VnYNu2TodOR8OxdWhGwrXirHA9s1xl\noFJhO9zlbQ2JS1KqJ1VjvJcp1ZMaOW0anxY9fZriSVWqJ1Wp8WnR+W6HW3bLP9tW2A5Hx31pQ3Ty\nVI3CdmReR8up9Xir5cJ2WLatVuuFO27HbrVMm3bU3M6ZNhNdCWdO/XrSlOxJ4SgN6AJCeAAJhUNt\nb8hovstRR4I6VH7srK8SVDffHVnVPByZXh+q7/Z23Q63vG6vwnY4cu0qHFAoHOqDCtvntJytgj/y\nmeCOl1Nx0TA/++7JlmXrG+vanOptCdvu3LzjdriVGp8mf0K6xqVOaBOaqZ60dsLVpxRPqlI8Kb1+\nutM/1KvUcGwcFQKxgBDuQ7ZtqzHcqEBTgxpCLV9Sb9DpUINqgzWqClap+pwjz2pVByujw61Dt66x\nttt9cDlcSmm+q3H4kEuiN2Uku5OV4klpHk6J3sDRdl5kerwr/px2W55I03IDS+TL8oE20wKhhjM3\np4TPnd9mneYbWlqeXBMIB86a3/bJNqdOn4r8TJufetMZh+WIhuZo7+h2jkjTOgzX3rjzEwDaM+hD\nOGyH1RBqaA7AQPNwQA2h02poeXpLqKHVcOSpLC3LtA3QM+tHpjdElw2cNRxofrpLd05dns1pOSOh\n6UnR2JQrmoPyzB2OkUBN0cih6XIEPW2+StAStn0VIE6HU4mORCXGJfZ6213R+jqhbdvRkD7zFJ1I\nqCe6EpXqSeUmFgD90oAO4YM1B7Tsvx9URcOpaIg22kHVB09Hg7cx3NinfXBYDsU7ExTv8kSf3JLm\nSYucPnXFN09rGY5c9/S4PPLGnRWo0aPQlGjYJroSuxSgsXTjSnssy4qervaa7gwAdMOADuHy+jK9\ne3SHGsNBxbsS5HF6lOhOiITgkLah53HGK6E5FFsCMr7NcHOItkxvHZqtlolsJ9JmvDO+x1+NAACg\nSwmSn5+v4uJiWZalnJwcTZkyJTqvoKBAb7zxhhwOhyZPnqyVK1f2WWfPNm34p/Tx1w63mRbrR4UA\ngIGj04tkO3fu1P79+7Vlyxbl5eUpLy8vOq+2tlYbNmxQQUGBNm3apNLSUn3wwQd92mEAAAaLTkO4\nqKhIWVlZkqSMjAxVVVWptjZyl25cXJzi4uJUX1+vUCik06dPKyUlpW97DADAINFpCJeXlystLS06\n7vP5VFZWJknyeDxavHixsrKyNGvWLE2dOlVjx47tu94CADCIdPuuIts+8yi12tpaPf/889q6dauS\nkpJ0991366OPPtKkSZM6XD8tLVEuV+8+Aelsfn/s3SNLzbEjFuum5tgQizV3GsLp6ekqLy+Pjp84\ncUJ+v1+SVFpaqtGjR8vn80mSZsyYod27d583hCsquv/Epu6IxRuzqDl2xGLd1BwbBnvNHf2B0enp\n6JkzZ2rbtm2SpJKSEqWnpyspKUmSNHLkSJWWlqqhoUGStHv3bl1++eW91GUAAAa3To+Ep0+frszM\nTGVnZ8uyLOXm5qqwsFBer1ezZ8/WggULNG/ePDmdTk2bNk0zZsy4GP0GAGDAs+zWF3kvgr4+3TDY\nT2m0h5pjRyzWTc2xYbDX3OPT0QAAoG8QwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEM\nAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEII\nAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQ\nwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAh\nhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBg\nCCEMAIAhhDAAAIYQwgAAGEIIAwBgiKsrC+Xn56u4uFiWZSknJ0dTpkyJzjt69KgeeughNTY26sor\nr9Tjjz/eZ50FAGAw6fRIeOfOndq/f7+2bNmivLw85eXltZm/du1affWrX9Vrr70mp9OpI0eO9Fln\nAQAYTDoN4aKiImVlZUmSMjIyVFVVpdraWklSOBzWH//4R332s5+VJOXm5mrEiBF92F0AAAaPTkO4\nvLxcaWlp0XGfz6eysjJJ0qlTpzRkyBB95zvf0R133KEnn3yy73oKAMAg06Vrwq3Ztt1m+Pjx45o3\nb55GjhyphQsXavv27brppps6XD8tLVEul7NHne0qv9/bp+33R9QcO2KxbmqODbFYc6chnJ6ervLy\n8uj4iRMn5Pf7JUlpaWkaMWKExowZI0m65ppr9Je//OW8IVxRUX+BXT4/v9+rsrKaPt1Gf0PNsSMW\n66bm2DDYa+7oD4xOT0fPnDlT27ZtkySVlJQoPT1dSUlJkiSXy6XRo0frr3/9a3T+2LFje6nLAAAM\nbp0eCU+fPl2ZmZnKzs6WZVnKzc1VYWGhvF6vZs+erZycHD3yyCOybVsTJkyI3qQFAADOr0vXhJcu\nXdpmfNKkSdHhyy67TJs2berdXgEAEAN4YhYAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEII\nAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQ\nwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAh\nhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGOIy3QEA\nwMX1zDP/oT17/qxTp06qoaFBI0aMVHJyivLz/71X2p8z51alpw+Xw3HmOG/9+hcuuN3f/e6/dfXV\n16q6ukobNjyvZctWXnCbphHCABBjHnjgQUnSz3/+M338canuv39Jr2/jiSeeVmJiYq+2uXlzgaZP\n/zsNHTpsUASwRAgDAJrt2vWeNm9+RfX19br//gf1rW/drzfffEeS9Oijy/SFL9yuSZP+Rvn5q1VT\nU6OmpiYtWfKwxo0b36X2P/e5m89p7/33/6i6ulodO3ZYn3zyV33jG9/SNdfM1Natb+q117bIsixl\nZ9+pxsZG/elPu7V06Tf0yCPf1urVj2rDhh9q16739MILz8nlcsnvT9eKFY/p7be36cMPP1BlZYUO\nHNivL3/5K7rlltv67Od2IQhhADBo1R8e1c9Kf9JmmsNhKRy2e9zmrRm3adW1a3q0bmnpPm3aVCi3\n293u/Fdf3aSrr75Wt956mz755GM99dQT+s//fK7HfZWkEyeO68UXX9TPfrZNP/3p65o69Sr94Aff\n18aNmxQMNiovL1dr167T97//PT3xxNOqqqqMrvvEE9/Rf/zHsxo+/BKtW/dv+uUvt8qyLJWW7tP3\nvveSDh06qNzcHEIYAND/jRs3vsMAlqT//d8PVVlZoW3bfi5JCgQa2l1u6dJvRK8Jp6amac2af+uw\nzSlTrpIkpaenq7a2Vn/96ycaM+ZyeTzx8njitXbtunbXq66ukmVZGj78EknS9Okz9MEHuzRhwiRN\nnjxFTqdTfn+66upqOy/cEEIYAAxade2ac45a/X6vyspqjPQnLi6u3emhUKh5vksPPviwJk+ect52\nOrsm3NKeJDmdzuiwbdtyOJyy7XAXemvJts+cMWhsbJRlOdpts7/iK0oAgHZZlqWGhgY1NDRo7949\nkqQrr5ys3/xmuyTpk08+1ubNr1xQe+257LLLdeDAftXX1ysQCGjJkvtk27Ysy6GmpqbocsnJybIs\nS8eOHZMkffDBLk2a9Dc9qNQcjoQBAO267bY5Wrjwbl1++RWaODESbnPmzFVe3irdd9+/KhwOa8mS\npRfUXnsSEhK0YMEiLVlynyRp7twvy7IsTZs2Xffdt0ArV66KLrts2aNavXqlnE6nRo4cpZtv/nu9\n9dYvelawAZZ9kY/T+/oUi8nTOKZQc+yIxbqpOTYM9pr9fm+70zkdDQCAIYQwAACGEMIAABhCCAMA\nYAghDACAIYQwAACG8D1hAIgxR48e0bx52Zo4cZIkKRgM6s4779aNN87qdluvv75FlZWVuuGGm/Sb\n32zXggVfb3e5ltcQdvRErtY+/nif1q377jmvP7zxxqv1t387NTo+dOhQrV79nW73+Wy//vXbmjUr\nS3/5y57z1tAXCGEAiEFjxlwWDbnq6irNn3+nPvOZa+TxxPeovfHjJ2r8+Ikdzm95DWFXQrgjSUlJ\nvfJe4rO98spGzZqV1WkNfaFLIZyfn6/i4mJZlqWcnBxNmXLuM0OffPJJffDBB/rhD3/Y650EAPSd\n5OQUDR06TCdPntTLL78olytO1dWVevzxtfrud/N05MhhhUIh/eu/LtKnPvV3eu+9nXr66Sfl8w3V\n0KHDNGLESO3a9Z4KC1/VmjXfPe9rCJ966v/qjTd+rLff3irLcuj662/SHXfcpWPHjum+++5XXFyc\nxo2b0OW+Hz16RI8+ulwbNkSyZ8GCr2jNmn/TSy+9oGHD/Nqz5886fvyYHntsjSZOnKSCgo3avv0d\nWZZDixbdr48++pP27durnJyHNWfO3GgN77zzS23ZUiCn06mJE/9GS5Ys1YYNz6uurlYHDuzX4cOH\noq9dvBCdhvDOnTu1f/9+bdmyRaWlpcrJydGWLVvaLLNv3z79z//8zwX9hQMAsWjIqkfl+VnbVxnK\nYcl3Aa8yDNx6m+pWdf1VhkePHlF1dZXS04dLijyTefnyldq69U0NHTpMK1Y8psrKSn3zm4u0ceNm\nPf/8en372/9H48dP0NKl39CIESOjbdXX1533NYRlZSe0ffs7eu65DZKke+9doFmzsvSLX/xYN9/8\n97r99jv0yis/0L59e3tcf4tgMKh169brJz95TVu3vqnExERt3/6Onn/+Bzpy5LBeeeUHeuSRb6ug\nYKPy8/9du3a911xDvV544Vm9/PL/U2JiopYtezA678SJ43riiae1Y8cf9NOfvt73IVxUVKSsrCxJ\nUkZGhqqqqlRbW6ukpKToMmvXrtWDDz6o9evXX1BnAAAXx4ED+3X//QslSW63W48+ulouVyQSrrwy\nU5K0e/eHKi5+Xx9++IEkKRAIqLGxUUePHtX48ZGj1auumq5AIBBtt7PXEP75zyU6dOigHnggct21\nvr5Ox44dUWlpqe68c74kadq0Gdqx4w/n9Lm2tjbaZ0nKyBin7Oy7Oqxx6tRpkiS/f7j+9KcS7d27\nR1deOVkOh0OjRo3WI498u931Dh48oFGjxkTfAjVt2qe0d+9Hks597eKF6jSEy8vLlZmZGR33+Xwq\nKyuLhnBhYaE+/elPa+TIkR01AQDoQN2qNecctfr9Xp3q4+cot74mfDaXKy76OW/eVzV79j+0md/y\nnmDp3NcEdvYaQpcrTtdcM1PLlq1sM/1HPyqIvoawo/XbuyZ87NjRNuPne0Wi0+lQuAtnGCyrbV2h\nUKM8Hk+7bV6obt+Y1XqjlZWVKiws1Msvv6zjx493af20tES5XM7OF7wAHT0oezCj5tgRi3VTc+8K\nBIbI5XK0u434+DilpCTI7/fqM5+ZoV/96lf68pe/pJMnT2rjxo166KGHdOmll6impkxjx45VSUmx\nrrrqKqWmJsrjidOnPjVZjz9+UImJDrlcLi1atEgvvfSSXC6n0tISdO21M/Tii88qKcml+Ph45eXl\naenSpRo7dqwOH/5Y11//ae3Z879yu13n9M+yrHOmud1hVVVVaNiwJJWXl+vo0cPy+Ya0qSMlJUHx\n8XG65poZeuWVl5WWlqDKykrl5ubq2Wefjf68W2qYNi1TR48eUkKCpaSkJJWUFOvee+9VUVGRkpLi\n5fd7VVExpN0+dlenIZyenq7y8vLo+IkTJ+T3+yVJO3bs0KlTp3TnnXcqGAzqwIEDys/PV05OToft\nVVTUX1CHOzPY38TRHmqOHbFYNzX3vlOn6hQKhdvdRkNDo6qqTqusrEYzZlyn7dt/qy9+8UtqamrS\nV7+6UGVlNZo//+tavPh+XXLJpfL5hqquLqDKynoFAo2qq2vSPfcs1F13zZMUeQ1heXmtpkyZpttv\nn6tnnnlBX/jCXM2de4ccDoduuOEm1dQ0at68eVq8+AG9+eYvlJExXsFg6Jz+2bbdTp8dmj797/Qv\n//J5jRs3XuPGTdCpU3Vt6qiqOq2GhkZ5PCm6+eZ/0Ny5d8i2bX3964tVVlajceMm6LbbPq977/1G\ntIZFix7QPffMl2U5NGXKVbrssol6++3tiotrUFlZjSoq6trtY0c6CutOX2W4a9cuPfPMM3r55ZdV\nUlKiNWvWaNOmTecsd+jQIa1YsaLTu6N5lWHvo+bYEYt1U3NsGOw1dxTCnR4JT58+XZmZmcrOzpZl\nWcrNzVVhYaG8Xq9mz57d6x0FACBWdOma8NKlS9uMT5o06ZxlRo0axXeEAQDoBp4dDQCAIYQwAACG\nEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACA\nIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMA\nYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIA\nABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQw\nAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABji6spC+fn5\nKi4ulmVZysnJ0ZQpU6LzduzYoXXr1snhcGjs2LHKy8uTw0G2AwDQmU7TcufOndq/f7+2bNmivLw8\n5eXltZn/2GOP6emnn9bmzZtVV1en3/72t33WWQAABpNOQ7ioqEhZWVmSpIyMDFVVVam2tjY6v7Cw\nUJdccokkyefzqaKioo+6CgDA4NLp6ejy8nJlZmZGx30+n8rKypSUlCRJ0c8TJ07o97//vb75zW+e\nt720tES5XM4L6XOn/H5vn7bfH1Fz7IjFuqk5NsRizV26JtyabdvnTDt58qQWLVqk3NxcpaWlnXf9\nior67m6yW/x+r8rKavp0G/0NNceOWKybmmPDYK+5oz8wOj0dnZ6ervLy8uj4iRMn5Pf7o+O1tbX6\n2te+piVLlui6667rha4CABAbOg3hmTNnatu2bZKkkpISpaenR09BS9LatWt1991364Ybbui7XgIA\nMAh1ejp6+vTpyszMVHZ2tizLUm5urgoLC+X1enXdddfpJz/5ifbv36/XXntNknTLLbdo7ty5fd5x\nAAAGui5dE166dGmb8UmTJkWHd+/e3bs9AgAgRvBUDQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGE\nAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMI\nYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQ\nQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAw\nhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAA\nDCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMCQLoVwfn6+5s6dq+zsbH344Ydt5v3hD3/Q\nnDlzNHfuXD377LN90kkAAAajTkN4586d2r9/v7Zs2aK8vDzl5eW1mb9mzRo988wz2rRpk37/+99r\n3759fdZZAAAGE1dnCxQVFSkrK0uSlJGRoaqqKtXW1iopKUkHDx5USkqKLr30UknSjTfeqKKiIo0b\nN65ve93MOn5cQ/JXy6qrOzPR45I3ELoo2+83qLldlm1fpM5cRB6XkmNwX1NzDOhHNTddconqVudL\nrk4j8oJ1uoXy8nJlZmZGx30+n8rKypSUlKSysjL5fL428w4ePHje9tLSEuVyOS+gy63sKZZe3SQ1\nNbWZHN87rQ8o1Bw7PKY7YAA1x4Z+U3NSkhLX5kk+b59vqtsxb1/g0UVFRf0Frd/GxKmy9u6XGgLR\nScOGJam8vLb3tjEAUPN5WFbfd+YiYl/HBmo2yx4yRGqKk8pqeq1Nv7/9QO80hNPT01VeXh4dP3Hi\nhPx+f7vzjh8/rvT09Avta7fY3mSpdW1+r2wr4aL2wThqjh1+r+xYOwdAzbEhFmtWF27MmjlzprZt\n2yZJKikpUXp6upKSkiRJo0aNUm1trQ4dOqRQKKRf//rXmjlzZt/2GACAQaLTI+Hp06crMzNT2dnZ\nsixLubm5KiwslNfr1ezZs7Vq1Sp961vfkiT90z/9k8aOHdvnnQYAYDCw7Au9yNtNZb14jr09fr+3\nz7fR31Bz7IjFuqk5Ngz2mju6JswTswAAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABD\nCGEAAAy56A/rAAAAERwJAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhLtMd6Ir8/HwVFxfL\nsizl5ORoypQp0XkFBQV644035HA4NHnyZK1cuVKhUEgrV67UgQMH1NTUpGXLlmnGjBn66KOPtGrV\nKknSxIkTtXr1akMVda63av7KV76i+vp6JSYmSpKWL1+uyZMnmyrrvLpb88mTJ7V8+XIFAgE1NjZq\nxYoVmjp16qDezx3VPJD2s9T9uluUl5frH//xH7V+/XpdffXVg3pftzi75oG0r7tbc2FhoZ566imN\nGTNGknTttdfq3nvvHVD7udvsfu7dd9+1Fy5caNu2be/bt8++/fbbo/NqamrsWbNm2Y2NjbZt2/b8\n+fPt999/337ttdfs3Nxc27Zte+/evfYXv/hF27Zt+6677rKLi4tt27bthx56yN6+fftFrKTrervm\nPXv2XNwCeqAnNb/00kv2G2+8EV1//vz5tm0P7v18vpoHwn627Z7V3eLhhx+2P//5z9s7duywbXtw\n7+sW7dU8EPZ1T2p+/fXX7bWocR/LAAAEXElEQVRr157T1kDZzz3R709HFxUVKSsrS5KUkZGhqqoq\n1dbWSpLi4uIUFxen+vp6hUIhnT59WikpKfrnf/5nrVixQpLk8/lUWVmpYDCow4cPR/8SmzVrloqK\niswU1Yneqnkg6UnN8+fP16233ipJOnr0qIYPHz7o93N7NQ80Pam7Zb0hQ4ZowoQJkjTo93XLeq1r\nHkh6WvPZBtJ+7ol+fzq6vLxcmZmZ0XGfz6eysjIlJSXJ4/Fo8eLFysrKksfj0ec+9zmNHTu2zfob\nN27ULbfcooqKCiUnJ0enDx06VGVlZRetju7orZpbPP3006qoqFBGRoZycnIUHx9/0Wrpqp7WXFZW\npkWLFqmurk4bN26Mif18ds0tBsJ+lnpWdzAY1LPPPqvnnntO+fn5kjTo93V7NbcYCPu6JzW///77\n2rlzpxYsWKBQKKTly5dr6NChA2Y/90S/PxI+m93qKZu1tbV6/vnntXXrVr3zzjsqLi7WRx99FJ1f\nUFCgkpISLV68+Lzt9HcXUvO8efO0bNkyFRQUyLIsFRQUXPT+90RXa/b7/Xr99de1YsWK6JmAjtrp\n7y6k5oG6n6Wu1f3CCy/oS1/6Uptfxudrp7+7kJoH6r7uSs1Tp07VAw88oA0bNmjJkiVavnz5edsZ\nDPr9kXB6errKy8uj4ydOnJDf75cklZaWavTo0fL5fJKkGTNmaPfu3Zo0aZJ+9KMf6Ve/+pWee+45\nxcXFnXOK9vjx40pPT7+4xXRRb9UsSbNnz46289nPflY///nPL2IlXdeTmqurqzVx4kSlpKToxhtv\n1LJlywb9fm6vZmng7GepZ3X/7ne/UzgcVkFBgQ4cOKAPP/xQ69atG9T7ur2an3rqqQGzr3tS85w5\nc5SRkSFJmjZtmk6dOqW0tLQBs597ot8fCc+cOVPbtm2TJJWUlCg9PV1JSUmSpJEjR6q0tFQNDQ2S\npN27d+vyyy/XwYMHtXnzZq1fv14ej0dS5BrEFVdcoffee0+S9NZbb+n66683UFHneqtm27Z1zz33\nqLq6WpL07rvvavz48QYq6lxPan7rrbf04x//WJK0Z88eXXrppYN+P7dX80Daz1LP6t68ebNeffVV\nvfrqq7rpppuUm5urSZMmDep93V7N48aNGzD7uic1v/jii/qv//ovSdLevXvl8/nkdrsHzH7uiX5/\nJDx9+nRlZmYqOztblmUpNzdXhYWF8nq9mj17thYsWKB58+bJ6XRq2rRpmjFjRvQv5IULF0bb2bBh\ng3JycvTYY48pHA5r6tSpuvbaaw1W1rHerPn222/XPffco4SEBA0fPlwPPPCAwco61pOar7jiCj3y\nyCP65S9/qWAwGP0Kw2Dez+3VbFnWgNnPUs/q7shg3tftGUj7uic1jxo1Sg8//LA2b96sUCikvLw8\nSQNnP/cErzIEAMCQfn86GgCAwYoQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAz5\n/6X19Ri35jxWAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "KjY_KnlE5ClG",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Drive the loss to a minimum."
+ ]
+ },
+ {
+ "metadata": {
+ "id": "JKiHjGN15HPX",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 567
+ },
+ "outputId": "c4c8150d-6aa2-41cd-d82e-5ec37655622a"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.00000999, n_epochs=1000000,interval=100000)"
+ ],
+ "execution_count": 26,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.1925572\n",
+ "Loss after epoch 100000 is 0.045763213\n",
+ "Loss after epoch 200000 is 0.03460842\n",
+ "Loss after epoch 300000 is 0.027004303\n",
+ "Loss after epoch 400000 is 0.021080853\n",
+ "Loss after epoch 500000 is 0.016473344\n",
+ "Loss after epoch 600000 is 0.012864709\n",
+ "Loss after epoch 700000 is 0.010056449\n",
+ "Loss after epoch 800000 is 0.007863842\n",
+ "Loss after epoch 900000 is 0.006151293\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.019056756\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3Xl8VPXd9//XzGSBkIUkTAIJawIk\nkABCqRS43DAUkcWlLlELVlFrq+1lLy1KaEu9fxWtVXtZl7tqobWYQkRBQL3RulBLpVIFWQJJYEAC\nCZAJWSCEkEzm/P5IMmQgG4EkJzPv5+PhI5mZc06+Hw7yzvmecz7HYhiGgYiIiJiGtasHICIiIt4U\nziIiIiajcBYRETEZhbOIiIjJKJxFRERMRuEsIiJiMgFdPYAGTueJDtt2ZGQIpaWVHbZ9s/LHulWz\nf/DHmsE/6/blmu32sGY/84sj54AAW1cPoUv4Y92q2T/4Y83gn3X7Y83gJ+EsIiLSnSicRURETEbh\nLCIiYjIKZxEREZNROIuIiJiMwllERMRkFM4iIiImY5omJGb0wgu/Jzd3NyUlx6iqqiIuLp7w8AgW\nL/7dRdn+TTfNIiYmFqv1zO9IL7746gVvd+PGfzBhwiScTidPP/0s8+cvvOBtiohI51E4t+AnP/kZ\nAO+/v459+xw8+OBDF/1nPPPMHwgJCbmo21yxIpNx475NXFysgllEpBtSOLfDli1fsmLFG1RWVvLg\ngz/j4Ycf5L33PgbgF7+Yz4033kJy8ggWL36cEydOUFtby0MP/ZyhQ4e1afszZlx9zva2bv2Kkycr\nyM8/QEHBIX7604eZOHEy69e/x1tvZWGxWEhPv4Oamhp27drJI4/8lKeffor//u+fsWTJMrZs+ZJX\nX32ZgIAA7PYYFiz4FR999AHbt39NWVkp+fkHuP32OcyceX2H/bmJiEjbdJtw/vXnv2Cd4512rWu1\nWnC7jXPen5V4Pb+e9Jt2bdPh2Mvy5asICgpq8vM331zOhAmTmDXrevbv38fzzz/D//7vy+36WQ2K\nio7yzDN/4N///pw1a95mzJhL+Mtf/sTrry+nurqGJ55YxFNPPcef/vRHnnnmD9hsNZ51n3nmSX7/\n+5eIje3Lc8/9lr//fT0WiwWHYy9//ONSDh06yKJFGQpnEZF6hmFQVHmU3NIc9pU5uGLAVQyJSOiU\nn91twtlshg4d1mwwA+zYsZ2yslI++OB9AE6frmpyuUce+annnHPv3pH85je/bXabo0dfAkBMTAwV\nFRV8881+Bg4cTHBwD4KDe/DUU881ud7x4+VYLBZiY/sCMG7ceL7+egvDhyeTmjoam82G3R7DyZMV\nrRcuIuJjDMPg8MlCcktyyC3dTV5JLrmlOeSV5lJ+usyz3F2p9/Dby5v+d/Zi6zbh/OtJv2n3Ua7d\nHnbRn3oVGBjY5Psul6v+8wB+9rOfk5o6usXttHbOuWF7ADbbmQbwhmFgtdowDHcbRmvBMM7MHNTU\n1GCxWJvcpoiIr3IbbgoqDpFXkkNuaS65JbvJK80htySXihrvjLBZbCREJPJf8ZeTFJnE8Khkvjt4\neqeNtduEs5lZLBaqquqOjPPycgEYOTKVzz7bQGrqaPbv38cXX3xOevr32729pgwaNJj8/ANUVlZi\ns9l49NGf8fvfv4TFYqW2tpaG3A0PD8disXDkyBH69u3L119vYfToS6itrb2AqkVEzMltuMk/fqAu\neBtCuCSHvNI8Kl0nvZYNtAaS2HsowyOTGR6ZRFJUMsMjk0nsPZQgW/Ozox1N4XwRXH/9Tdx3350M\nHpxAUtIIAG666VaeeOLX/PjH9+B2u3nooUcuaHtN6dmzJ/Pm3c9DD/0YgFtvvR2LxcLYseP48Y/n\n8bvfPe1Zdv78X/D44wux2WzEx/fn6qu/y4cf/r92Viwi0vVq3bUcOL6f3NJc8kpyyCnZTV5pLnvL\n8jjlOuW1bJA1iMTew0iOSmZ4fQAnRSYzJCKBQFvTM6FdyWKYZC7zYk87N9YR09rdgT/WrZr9gz/W\nDP5Zt90eRuGREr45vp/ckhzySuv+yynJwVG2h9O1p72W72HrwdDI4QyPTCI5akRdCEclMSh8CAFW\ncx2P2u1hzX5mrpGKiIjfqq6tZl+5o/6ccA55Jbk4TuSRW5xLjbvGa9mQgBCSo0Z6pqKTokYwPDKJ\ngWGDsFltzfyE7kPhLCIinep07Wn2lu6pPydcF8J5pTnsK3fgcru8lg0NCmVUn9GNpqKTSIoaQf+w\nAVgtvtuBWuEsIiId7kT1cT78Zj3rHGv4JP/vVNV6314aFhTOJfZxnguykqKSGB6ZzCVDRlBc7H+3\neSqcRUSkQ5SfLmP9/vd5d98aPs3/mGp3NQDDI5OY0G+S5xalpMhk+vbqh8ViOWcbTb3nDxTOIiJy\n0ZRUHWP9/vdZ53iHzw5t8JwrHhGVwuyh1zMz4TqSopK7eJTmp3AWEZELUnyqmP+3/13W7l3NxoLP\nqDXqeiiM6jOGWYnXMTPhOoZGtu3ZAlJH4dyCw4cLmTs3naSkut/yqqurueOOO7niiqvOe1tvv51F\nWVkZl19+JZ99toF5837Y5HINj3tsrgNZY/v27eW5554+5zGTV1wxgVGjxhAUFEB1tYvo6Ggef/zJ\n8x7z2T799COuuiqNPXtyW6xBRHzf0cqjvL9vHe861vCvwn/iru9WODZmHDMTr2dmwuxO60PtixTO\nrRg4cJAn/I4fL+euu+7gO9+ZSHBwj3Ztb9iwJIYNS2r284bHPbYlnJsTGhrKiy++etHviXzjjde5\n6qq0VmsQEd90uKKQ9/atZd2+Nfy78HMM6tpkjI+9lFmJ1zMjYRYDwwd18Sh9g8L5PISHRxAd3Ydj\nx47x5z+/RkBAIMePl/F//s9TPP30ExQWFuByubjnnvv51re+zZdfbuYPf3iWqKhooqP7EBcXz5Yt\nX7Jq1Zv85jdPt/i4x+ef/7+sXbuajz5aj8Vi5bLLruS2275PUdFRfvnLxwgMDGTo0OFtHvvhw4X8\n4hePsmTJMgDmzZvDb37zW5YufZU+fezk5u7m6NEj/OpXvyEpKZnMzNfZsOFjLBYr99//IDk5u9i7\nN4+MjJ9z0023emr4+OO/k5WVic1mIylpBA899AhLlrzS5OMtRaT7OXTiIO/uW8M6xxr+c+QLACxY\nmNBvIrMSr2NGwmziQuO7eJS+p9uEc69f/4Lgde17ZCRWC1FNPDLy9KzrOfnrtj9M4/DhQo4fLycm\nJhao61n96KMLWb/+PaKj+7Bgwa8oKyvjv//7fl5/fQWvvPIiv/zl/8ewYcN55JGfEhd35i9wZeXJ\nFh/36HQWsWHDx7z88hIAfvSjeVx1VRqrVmVx9dXf5ZZbbuONN/7C3r157fszaaS6uprnnnuRd955\ni/Xr3yMkJIQNGz7mlVf+QmFhAW+88Rcee+yXZGa+zuLFv2PLli/ra6jk1Vdf4s9//hshISHMn/8z\nz2dnP95S4SzSfRw4/g3vOtby7r53+Opo3f/TVouVyXGXMTPxOmYmzCa2V98uHqVv6zbh3FXy8w/w\n4IP3ARAUFMQvfvE4AQF1f2wjR6YAsHPndrZt28r27V8DcPr0aWpqajh8+DDDhtUd3V5yyThOnz7T\nZq61xz3u3p3NoUMH+clP6s7rVlae5MiRQr75Zj9XXZUGwNix4/n3vz8/Z8wVFRU8+OB9nnPOiYlD\nW3zoxpgxYwGw22PZtSubvLxcRo5MxWq10r//AB577JdNrnfwYD79+w/0PFVr7NhvkZeXA5z7eEsR\nM9tRvJ0/73iN9d+8R3SPPiT2HkZi76Ek9h5KQu+hDO09jOge0T59W8++cgfvOuqOkLc5twJ1T2a6\nvP9VzEq8julDZhITEtPFo/Qf3SacT/76N+d1lNuY3R5GSTvPvTY+53y2gIBAz9e5c+9m6tRrvD5v\neE4znPs4xtYe9xgQEMjEiZOZP3+h1/uZma97HvfY3PpNnXM+cuSw1zItPYrSZrPibmKm4WwWi3dd\nLlcNwcHBTW5TxGyqa6tZ53iHpTtf80zX2nvGUFBRQG5pzjnLRwT3JjEi8ZzgTohIpFdgr84e/kWx\npzSPdY53WOdYQ/axHQAEWAOYMjCNWQnXc82QGUT3jO7iUfqnNoXz4sWL2bZtGxaLhYyMDEaPPvOM\n4szMTNauXYvVaiU1NZWFC8+ESXFxMdOnT+fFF19kwoQJF3/0JjFyZCobN/6DqVOvobS0hDffXM4P\nf/gAffrYyc//hgEDBrF161ekpIzyrNPa4x6Tkkbwf//vC1RVVREcHMzzzz/Lj370IAMHDiInZxfJ\nySM8U8htERLSi9LSEgzDoKTkGIWFh5pdNilpBH/5yxJcLhfHj5fzu989yZNPPnNOYA8YMIhDh/Kp\nrDxJSEgvtm7dwp13zuPLL784/z9EkU5ScOIQf921lGW7Xqf4lBOAKQPTuDv1Xq4e+F2sFitFp4rY\nV7YXh+e/PTjK9rKjeDtbir46Z5txveI9gd04uAeGDTLVwxYMwyCnZDfrHO/w7r415JTsBuqe2PTd\nQdcwM/E6rhl8Lb17RHbxSKXVvzWbN2/mwIEDZGVl4XA4yMjIICsrC6ibPl2yZAkffvghAQEB3H33\n3Xz99ddcckndlObTTz/NgAEDOrYCE5gyJY0tW/7D/fffTW1tLXffXTcNft99P+YXv3iUvn37ec5T\nN2jtcY8vvPAqt9xyGw88cC9Wq5XLL7+S4OAe3Hzzbfzyl4/x2WefkpjY9vsGw8PDGT/+Uu65Zy5D\nhw5r8Wrrfv3imDbtWh588D4Mw+CHP3wAgOHDk7j33rn86Ec/9dTwwAP/zcMP/wSLxcro0ZcwZswl\nCmcxHcMw+GfBP1i64zU++OZ9ao1aIoJ7c/+YB/lB6jwSIhK9lo8NiSU2JJaJcd7XSrjcLg6eyPeE\ntaNsL45yB47SPfyz4B/8s+AfXssHWgMZHD7Ea3q84fuYnjGdMk1uGAbZx3bybv0R8p6yuutUgm3B\nXDNkBrMSrmPa4OmEB0d0+Fik7Vp9ZOTzzz9PXFwcN998MwDXXHMNb731FqGhoZw+fZrZs2ezcuVK\nQkJCmDNnDosXL2bIkCFs2rSJDz/8kFOnTnHDDTe0euSsR0ZefP5Yt2r2D22t+UT1cd7MXc7SHa95\nQmlUnzHcnXovNwy7iZDAkIs2ppM1J9lfvo99ZXvZWx/e+8r3srdsL+Wny85ZPiwonMSIRBLqj7Q9\nwR2RSGhQ048SbGvdhmGw3fk16xxrWLfvHfaX7wOgZ0BPrh74XWYlXsfUQdOa/Tlm4st/vy/okZHF\nxcWkpKR4XkdFReF0OgkNDSU4OJgHHniAtLQ0goODmTFjBkOGDKG6upqXXnqJl19+mcWLF1+cKkRE\n2iinZDdLd7zKyrwsTtZUEGgN5HvDbuHuUfcyPvbSDjli7RXYi9Q+o0jtM8rrfcMwOFZ1rC6szwru\nXcey+br+4qvGYkP6MrT3sEbBXfe1d9Soc5Zt/HO2FH3JOsca3nWsIf/EAQBCAnpx/dAbmZV4PVMG\nTu2258f9zXmfDGl8oF1RUcErr7zC+vXrCQ0N5c477yQnJ4ePPvqIm2++mfDw8DZvNzIyhICAjnsG\nZ0u/ofgyf6xbNfuHs2uuqa3hnZx3eOk/L/GPA3XTy/3D+7Pgvx7jnnH3EBsa29RmOkUM4YwYOASY\n6vV+rbuW/PJ88o7lef7LPZZL3rE8Pi/cyL8K/+m1vM1iIyEygaQ+SQyPGs7w6OHEhcXx6Tef8tau\ntzh4/CAAYUFh3DHqDm4aeRPTEqfRM7BnZ5XaIfzx73er4RwTE0NxcbHndVFREXa7HQCHw8GAAQOI\niooCYPz48ezcuZONGzfidrvJzMwkPz+f7du38/zzzzNsWPPnSEtLKy+0lmb58rRIS/yxbtXsHxrX\nfPTkEf66688s2/UXjpysuyvhsv5XcnfqvUwbPL3ugqxT4Dxlzj+jUPowLqIP4yImQaNul6dcp/im\nfD97y/bUXZxWvpf8k/vJcebwbt6752wnPCiCW5JuY3bi9Vze/yp6BNR1Mawoc1GBOWtvC1/++31B\n09qTJ0/mhRdeID09nezsbGJiYggNDQUgPj4eh8NBVVUVPXr0YOfOnVxxxRWsWLHCs/5jjz3GDTfc\n0GIwi4icD8Mw2FT4L5bueI339q/F5XYRFhTOPaN+yF2p9zIssu3d88yqZ0BPRkSPZET0SM97DUFV\nUnWMfWUO9pbt4dCJg4yNGcdl/a8kyBbUhSOWi6nVcB43bhwpKSmkp6djsVhYtGgRq1atIiwsjKlT\npzJv3jzmzp2LzWZj7NixjB8/vjPGLSJ+qKKmgrfz3uSvu5ewo6juvtwRUSO5K/Vebkq6ldDA0C4e\nYeeI6hFNVN9oxve9tKuHIh2k1au1O4uu1r74/LFu1eyb9pbu4c87X2NF7t84UX2cAGsAM4bM5u5R\n9/KdfpN8unNXY/6wr8/myzVf0LS2iEhXcLldfPjNepbufI3PDn0K1F3FfP+YB3josgcJrPK/i4TE\nfyicRcRUnJVOMne/zuvZSymoqOtkNynuv7g79V6mD5lJoC0Qe1gYzirfPJoSAYWziJiAYRh8eXQz\nS3e8xjrHO1S7qwkJ6MWdKfO4O/Ver4uiRPyBwllEukxlTSXv7H2bJTteZUfxNgCG9R7OXan3cEvS\nbWopKX5L4SwinW5/+T7+snMJy3OWUXa6DKvFyrVDZnH3qHu5LP4Kv7nAS6Q5CmcR6RS17lo+yf87\nS3e+xif5H2Fg0KennZ996xHmjryb+LD+XT1EEdNQOIuYnLPSyZdHN2OzWAmyBRNsCybIFlT3vTWY\nEwFRnKiorv+s7v0ga5Bpjj5Lqo7xt91v8JfsJeQf/waAb/edwN2p9zIz8TqCbcFdO0ARE1I4i5hQ\nrbuWTw9+RObuZXzwzfu43K7z3kaQNcg7sG1B9cHuHeIN7zV8HmgN8nx+Zt3gRu/V/3JgbeK9Rt87\nK4v4664/886et6mqraJnQE/uGDGXu1PvZZR9TAf8qYn4DoWziIl8U76fFTlvsDwnk8MnCwEYEZXC\ndUNvIMgWTHXtaaprT3O6ttrz1Rrk5vjJk1R73jtNtbv6rOVOU11bTUX1Cc971e7qTqlpcPgQ7kq9\nl9uS76B3j8hO+Zki3Z3CWaSLVbmqeG/fWv62exn/LKh7mlJYUDhzR97NHSPmcEnMuBanqNvbQckw\njCZDvKa2htPu0/W/CFTXB/uZZbzec1c3+QtDde1pAqwBzEq8jisHXI3VYm33n4+IP1I4i3SRHc5t\nZO7+K2/vWUn56TIAJsZN5vbkOcxKvJ6QwJAO/fkWi4Xg+mlo9doSMReFs0gnKqsq5e09K/nb7mWe\n+3pjQmL56dj/4fYR3yeh99AuHqGImIHCWaSDuQ03/yr4J5m7/8r7+9ZRVVuFzWLjmiEzuGPEXK4e\nOLXumcMiIvX0L4JIBzlcUciKnEz+lrOMA/W3ECX2HsrtI+ZyS9JtxIbEdu0ARcS0FM4iF1F1bTUf\nfrOev+3+K58c/Ai34SYkIIRbk27njhFzmdBvomnuPxYR81I4i1wEeSW5ZO7+KyvzllN8qhiAcTHf\n4vYRc7lh2PcICwrv4hGKSHeicJZ2q6mt4UTNcSKDo/zyaLCipoI1e1aRufuvfHl0MwBRPaL44egf\nc/uIuXqSkoi0m8JZzktNbQ0bCz5jzd5VvL9/HWWny4gMjmRYZBLDI5MYHlX3dVhkEvGh/X3u/taG\nRxv+bfcy3tm7ipM1FViwcNWAq7ljxFymDblW7ShF5IIpnKVVLreLfxX8k7WO1by3by0lVSUA9O3V\nj7TYS9lX7uDLo5vZfOTfXuuFBIQwNHJ4XWjXB/bwyCQGhw8h0BbYFaW0m7PSycq8Ffxt91/JK80F\nYEDYQB645KekJ99B/7ABXTxCEfElCmdpUq27lk2H/8Wavat5b98az3nUmJBY7hn1Q2YPvZFL+07w\nHBmfrj3NvjIHe0pzySvNZU9pLrmlueSW7Ga782uvbQdaAxkSkcDwyGSGRw73hHZi72Ed3njjfDTV\n3zrIGsQNQ7/H7SPmcln/K3xuZkBEzEHhLB617lo2H/k3a/auYp1jDc5TRQD06WnnrtR7uC7xRib0\nm4jNajtn3WBbMCOiR55znrXWXUv+iQP1oZ1HXmlOo+9zvZa1YGFA2ECvo+y6r8M7tSfzN+X7WZ6z\njBU5f/P0tx4ZncodI+bwveG3ENUjutPGIiL+SeHs59yGm/8c2czavatY63iHo5VHAIjuEc3ckXdz\n/bAbmdhvcpOB3BY2q40hEQkMiUjgu4One943DIOjlUfOHGWX5LCnPrA/yv+Qj/I/9NqOvWcMSVHJ\nDKufJm8I79iQvhflYrRTrlO8v28dmbv/ysaCz4C6/tZ3pszjjhFzGGMf65cXvYlI11A4+6GGi5rW\n7l3NWsc7nqPDyOBIvj/iTq4beiOT4y/r0K5VFouFvr360bdXPy7vf6XXZ2VVpZ6j7Ibw3lOax8aC\nzzzB2SA8KMIrsL89+BJirAMYGDaoTb9QNNXfelLcf3H7iDnMTLjOVNPsIuI/FM5+wjAMthZ9xZq9\nq1nneIdDFQcBiAjuze3Jc5g99AYui7/CFBdq9e4RyaX9JnBpvwle71fWVOIo20Nuo6nxPaW5bHNu\n5auj/6lbaFPdlx62HiT2HuZ1TntYZBIJvRM5VVN5Tn/r2JC+/GDcw9w24vskRCR2ZrkiIudQOPsw\nwzDYVrSVNY7VrN27mvwTB4C6o81bk27nuqE3cHn/qwiyBXXxSNsmJDCEUfYxjLKP8Xq/praGb47v\nJ7ckh8Lqb9h6aDt7yvLYW5pH9rEdXsvaLDZsFhvV7mpsFhvTh8zkjhFzmKL+1iJiIvrXyMcYhsHO\nYztYu3c17+5/B0epA4DQwDBuGn4r1w+9kSsGTPGpe3EDbYEMixzOsMjhXs82dhtuDp046HWUnVea\nS1VtFdcNvVH9rUXEtBTOPsAwDHaX7GLN3rdZs3c1+8rrAzkolBuH3cx1Q2/kqgFX0yOgRxePtHNZ\nLVYGhg9iYPggrh703a4ejohIm7UpnBcvXsy2bduwWCxkZGQwevRoz2eZmZmsXbsWq9VKamoqCxcu\nxOVysXDhQvLz86mtrWX+/PmMHz++w4rwVzklu1mzdxVr965mT1keUNf44/qhNzI78UbSv3UjFWWu\nLh6liIicr1bDefPmzRw4cICsrCwcDgcZGRlkZWUBUFFRwZIlS/jwww8JCAjg7rvv5uuvv8bhcNCz\nZ0+WL1/Onj17WLBgAW+99VaHF+MP9pTm1QWyYzU5JbsB6BnQk1mJ13Nd4g2kDZrmucK4Z2BPKjjR\nlcMVEZF2aDWcN23aRFpaGgCJiYmUl5dTUVFBaGgogYGBBAYGUllZSUhICKdOnSIiIoLZs2czc+ZM\nAKKioigrK+vYKnyco2wPa/auZs3e1ewuyQbqrkaekTC7LpAHTyM0MLSLRykiIhdLq+FcXFxMSkqK\n53VUVBROp5PQ0FCCg4N54IEHSEtLIzg4mBkzZjBkyBCv9V9//XVPUEvb7S/fx9q9q1njWM3O4u0A\nBFmDuGbIDK5LvIFpg6cTGhTWxaMUEZGOcN4XhBmG4fm+oqKCV155hfXr1xMaGsqdd95JTk4OycnJ\nQN356OzsbP74xz+2ut3IyBACAtrXhaot7HbzB9n+0v2s3LWSN7Pf5KvDXwF1fahnDp/JLSNvYXbS\nbCJ6RJzXNrtD3RebavYP/lgz+Gfd/lhzq+EcExNDcXGx53VRURF2ux0Ah8PBgAEDiIqKAmD8+PHs\n3LmT5ORkVq5cySeffMLLL79MYGDrjS1KSyvbW0OrGt9eYwaGYXCo4iC7jmWTXbyDXcey2XVsJ3vL\n9gAQYA3g6oFTuW7ojUwfMoOI4N4AVJ8A54m212G2ujuDavYP/lgz+GfdvlxzS790tBrOkydP5oUX\nXiA9PZ3s7GxiYmIIDa07vxkfH4/D4aCqqooePXqwc+dOrrjiCg4ePMiKFSt44403CA72nftp26Oi\npoKcY7vIPraTXcd21gdxNieqj3stFx4UwZSBacxOvIHpQ2YQ2SOqi0YsIiJdrdVwHjduHCkpKaSn\np2OxWFi0aBGrVq0iLCyMqVOnMm/ePObOnYvNZmPs2LGMHz+e5557jrKyMu677z7PdpYsWUJQUPfo\nRNUebsPNgePfkF3cOIR38s3x/V7LWS1WhvYextUD0xgZncrI6BRGRqcSH9pfD1YQEREALEbjk8hd\nqCOnLS72tMjx0+XsKtnlNSW9+9guKl0nvZaL6hFFSvQoTwCPjE5heFQyPQN6XrSxtMSXp4Oao5r9\ngz/WDP5Zty/XfEHT2v6s1l3L/vJ9ZB/b4TUlffBEvtdyAdYAhvVOqgvhPqmk1IfxxXqcoYiI+BeF\nc72SqmN14Vt8Zko6p2Q3VbVVXsvFhMRy5YApXlPSwyOTus3DI0RExPz8LpxramvYW7bH67zwrmPZ\nnmcaNwiyBpEUNcJrSnpkdCr2EHsXjVxERPyFT4dzUWURu47tJH/PXjbnf8WuY9nkleRQ7a72Wi6u\nVzxpA79bF8J96kI4MWKoKZ5tLCIi/scnw/mZ/zzFn3f+CeepIq/3ewb0JKVPqteR8MjoFN22JCIi\npuKT4XzwRD49A3pyzeBrGRmdwneGfJsBQYkMDk/AZu24LmQiIiIXg0+G8/NTXvZ67cuX4ouIiO+x\ndvUARERExJvCWURExGQUziIiIiajcBYRETEZhbOIiIjJKJxFRERMRuEsIiJiMgpnERERk1E4i4iI\nmIzCWURExGQUziIiIiajcBYRETEZhbOIiIjJKJxFRERMRuEsIiJiMgpnERERk1E4i4iImIzCWURE\nxGQUziIiIiajcBYRETEZhbOIiIjJBLRlocWLF7Nt2zYsFgsZGRmMHj3a81lmZiZr167FarWSmprK\nwoULqamp4bHHHqOwsBCbzcaTTz7JgAEDOqwIERERX9LqkfPmzZs5cOAAWVlZPPHEEzzxxBOezyoq\nKliyZAmZmZksX74ch8PB119/zbvvvkt4eDjLly/n/vvv59lnn+3QIkRERHxJq+G8adMm0tLSAEhM\nTKS8vJyKigoAAgMDCQwMpLJ3cTlGAAAdXElEQVSyEpfLxalTp4iIiGDTpk1MnToVgEmTJrFly5YO\nLEFERMS3tDqtXVxcTEpKiud1VFQUTqeT0NBQgoODeeCBB0hLSyM4OJgZM2YwZMgQiouLiYqKAsBq\ntWKxWKiuriYoKKjZnxMZGUJAgO0ilNQ0uz2sw7ZtZv5Yt2r2D/5YM/hn3f5Yc5vOOTdmGIbn+4qK\nCl555RXWr19PaGgod955Jzk5OS2u05zS0srzHUqb2e1hOJ0nOmz7ZuWPdatm/+CPNYN/1u3LNbf0\nS0er09oxMTEUFxd7XhcVFWG32wFwOBwMGDCAqKgogoKCGD9+PDt37iQmJgan0wlATU0NhmG0eNQs\nIiIiZ7QazpMnT+aDDz4AIDs7m5iYGEJDQwGIj4/H4XBQVVUFwM6dOxk8eDCTJ09m/fr1AHz66adM\nmDCho8YvIiLic1qd1h43bhwpKSmkp6djsVhYtGgRq1atIiwsjKlTpzJv3jzmzp2LzWZj7NixjB8/\nntraWj7//HNuu+02goKCeOqppzqjFhEREZ9gMdpyQrgTdOQ5BV8+Z9ESf6xbNfsHf6wZ/LNuX675\ngs45i4iISOdSOIuIiJiMwllERMRkFM4iIiImo3AWERExGYWziIiIySicRURETEbhLCIiYjIKZxER\nEZNROIuIiJiMwllERMRkFM4iIiImo3AWERExGYWziIiIySicRURETEbhLCIiYjIKZxEREZNROIuI\niJiMwllERMRkFM4iIiImo3AWERExGYWziIiIySicRURETEbhLCIiYjIKZxEREZNROIuIiJiMwllE\nRMRkAtqy0OLFi9m2bRsWi4WMjAxGjx4NwNGjR3nkkUc8yx08eJCHH36YSy+9lIyMDKqrq3G73SxY\nsIDU1NSOqUBERMTHtBrOmzdv5sCBA2RlZeFwOMjIyCArKwuA2NhYli1bBoDL5WLOnDlMmTKFF198\nkalTp5Kens6WLVv4/e9/z5IlSzq2EhERER/R6rT2pk2bSEtLAyAxMZHy8nIqKirOWW716tVMmzaN\nXr16ERkZSVlZGQDHjx8nMjLyIg9bRETEd7V65FxcXExKSorndVRUFE6nk9DQUK/lVq5cydKlSwH4\nwQ9+wE033cQ777xDRUUFy5cvv8jDFhER8V1tOufcmGEY57y3detWEhISPIH9pz/9ienTp/OjH/2I\nTz/9lN/+9re8+OKLLW43MjKEgADb+Q6nzez2sA7btpn5Y92q2T/4Y83gn3X7Y82thnNMTAzFxcWe\n10VFRdjtdq9lNmzYwMSJEz2vt2zZwkMPPQTA5MmTefzxx1sdSGlpZZsHfb7s9jCczhMdtn2z8se6\nVbN/8MeawT/r9uWaW/qlo9VzzpMnT+aDDz4AIDs7m5iYmHOmtHfs2EFycrLn9aBBg9i2bRsA27dv\nZ9CgQe0auIiIiD9q9ch53LhxpKSkkJ6ejsViYdGiRaxatYqwsDCmTp0KgNPpJDo62rPOD3/4QxYu\nXMj69esBWLhwYQcNX0RExPdYjKZOIneBjpy28OVpkZb4Y92q2T/4Y83gn3X7cs0XNK0tIiIinUvh\nLCIiYjIKZxEREZNROIuIiJiMwllERMRkFM4iIiImo3AWERExGYWziIiIySicRURETEbhLCIiYjIK\nZxEREZNROIuIiJiMwllERMRkFM4iIiImo3AWERExGYWziIiIySicRURETEbhLCIiYjIKZxEREZNR\nOIuIiJiMwllERMRkFM4iIiImo3AWERExGYWziIiIySicRURETEbhLCIiYjIKZxEREZNROIuIiJhM\nQFsWWrx4Mdu2bcNisZCRkcHo0aMBOHr0KI888ohnuYMHD/Lwww8za9YslixZwtq1awkICGDRokWe\ndURERKRlrYbz5s2bOXDgAFlZWTgcDjIyMsjKygIgNjaWZcuWAeByuZgzZw5Tpkxhz549vPfee7z9\n9tvk5uby8ccfK5xFRETaqNVw3rRpE2lpaQAkJiZSXl5ORUUFoaGhXsutXr2aadOm0atXLz799FOm\nT59OQEAAKSkppKSkdMzoRUREfFCr4VxcXOwVrlFRUTidznPCeeXKlSxduhSAgoICbDYb8+bNw+Vy\nsWDBApKTk1v8OZGRIQQE2NpTQ5vY7WEdtm0z88e6VbN/8MeawT/r9sea23TOuTHDMM55b+vWrSQk\nJHgC2zAMamtr+dOf/sRXX33FwoULefvtt1vcbmlp5fkOpc3s9jCczhMdtn2z8se6VbN/8MeawT/r\n9uWaW/qlo9VwjomJobi42PO6qKgIu93utcyGDRuYOHGi53WfPn1ISEjAYrEwfvx4CgoK2jNuERER\nv9TqrVSTJ0/mgw8+ACA7O5uYmJhzprR37NjhNW19+eWXs3HjRgAcDgf9+vW7mGMWERHxaa0eOY8b\nN46UlBTS09OxWCwsWrSIVatWERYWxtSpUwFwOp1ER0d71rnkkkv47LPPuPXWWwH41a9+1UHDFxER\n8T0Wo6mTyF2gI88p+PI5i5b4Y92q2T/4Y83gn3X7cs0tnXNWhzARERGTUTiLiIiYjMJZRETEZBTO\nIiIiJqNwFhERMRmFs4iIiMkonEVERExG4SwiImIyCmcRERGTUTiLiIiYjMJZRETEZBTOIiIiJqNw\nFhERMRmFs4iIiMkonEVERExG4SwiImIyCmcRERGTUTiLiIiYjMJZRETEZBTOIiIiJqNwFhERMRmF\ns4iIiMkonEVERExG4SwiImIyCmcRERGTUTiLiIiYjMJZRETEZNoUzosXL+bWW28lPT2d7du3e94/\nevQoc+bM8fx35ZVXsm7dOs/nxcXFfPvb3+aLL764+CMXERHxUQGtLbB582YOHDhAVlYWDoeDjIwM\nsrKyAIiNjWXZsmUAuFwu5syZw5QpUzzrPv300wwYMKCDhi4iIuKbWj1y3rRpE2lpaQAkJiZSXl5O\nRUXFOcutXr2aadOm0atXL896vXr1Yvjw4Rd5yCIiIr6t1XAuLi4mMjLS8zoqKgqn03nOcitXruSm\nm24CoLq6mpdeeomf/exnF3GoIiIi/qHVae2zGYZxzntbt24lISGB0NBQAF599VVuvvlmwsPD27zd\nyMgQAgJs5zucNrPbwzps22bmj3WrZv/gjzWDf9btjzW3Gs4xMTEUFxd7XhcVFWG3272W2bBhAxMn\nTvS83rhxI263m8zMTPLz89m+fTvPP/88w4YNa/bnlJZWtmf8bWK3h+F0nuiw7ZuVP9atmv2DP9YM\n/lm3L9fc0i8drYbz5MmTeeGFF0hPTyc7O5uYmBjPEXKDHTt2cO2113per1ixwvP9Y489xg033NBi\nMIuIiMgZrYbzuHHjSElJIT09HYvFwqJFi1i1ahVhYWFMnToVAKfTSXR0dIcPVkRExB9YjKZOIneB\njpy28OVpkZb4Y92q2T/4Y83gn3X7cs0tTWurQ5iIiIjJKJxFRERMRuEsIiJiMgpnERERk1E4i4iI\nmIzCWURExGQUziIiIiajcBYRETEZhbOIiIjJKJxFRERMRuEsIiJiMgpnERERk1E4i4iImIzCWURE\nxGQUziIiIiajcBYRETEZhbOIiIjJKJxFRESaU1WFdZ+DgH9vwnLieKf92IBO+0kiIiJmUl2N9XAh\ntsICrAWHsBYWYis8hLWwAGtBQd33x455Fj817z4qnnymU4amcBYREd/jcmE9cvhMyBYWYi08hK2g\nAGvDa2cRFsNocnWjZ09q4+JxjRyFOz6e2rg4qm65vdOGr3AWEZHupbYWa9HRuqPdw4XYCg7Vh3Cj\n4D16BIvb3eTqRnAw7n5x1Ez6L9xx8bjj4qmNi68P4f644+MxekeCxdLJhZ2hcBYREfNwu7E4nZ6j\nXY4X0yvXUXfUW1hYN+V85DAWl6vJ1Y3AwLrgvfQ7Z4I3Ph53fejW9ovH6NOnS4O3LRTOIiLSOQwD\ny7Fj2A7XndO1Fhw6c773cGHdlPORQizV1V6rhTSsbrPh7tsP19hv1R3pnnW0646Lx22PAWv3v9ZZ\n4SwiIhfOMLCUldZNLzeEb2FB3ZTz4cK6ID5ciKWqqunVLRbcsX1xjRqNu9+Zo93QEUMpDY2qC96Y\nWAjwj9jyjypFROSCWI6X1wXu4YK6I1zPUW/9e4UFWCorm13fbY/BlTzCK3gbppnd8fG4+/aDwMBz\n1gu1h+FynujI0kxJ4Swi4u8qKjzTy7b6o1zvo94CrBXNB6Q7OhpX4jDccXH153j7108596e2Xxzu\nfnEQHNyJBXV/CmcREV9WWek9zdxwtNv4AqvysmZXd/fujXvgIGri43H3azjHWxe87rg4avvFQ8+e\nnViQf2hTOC9evJht27ZhsVjIyMhg9OjRABw9epRHHnnEs9zBgwd5+OGHmT59OgsXLiQ/P5/a2lrm\nz5/P+PHjO6YCERF/dfp0o8BtdFtRYf3U8+ECrCUlza7uDgvHHR+P61vjPRdYeY56628volevTixI\nGrQazps3b+bAgQNkZWXhcDjIyMggKysLgNjYWJYtWwaAy+Vizpw5TJkyhTVr1tCzZ0+WL1/Onj17\nWLBgAW+99VbHViIi4ktqas7pXkVpEeF799cH8iGsxcXNrm6E9KI2Ph7XqDF1gdsvrm6audFRrxEW\n3okFyfloNZw3bdpEWloaAImJiZSXl1NRUUFoaKjXcqtXr2batGn06tWL2bNnM3PmTACioqIoK2t+\nykRExO+4XFiPHjnryuazulcVHW2ye1UwYPToUde9akQK7n5x3hdYxdUHb0Rv09/LK81rNZyLi4tJ\nSUnxvI6KisLpdJ4TzitXrmTp0qUABDa64u7111/3BLWIiM+rrcXqLPLu1Xz2bUVHDjffvSooqK6J\nxsTJZ3Wv6k9E6nCKe/bGiIxS8Pq4874gzGjiN7mtW7eSkJBwTmBnZmaSnZ3NH//4x1a3GxkZQkCA\n7XyH02Z2e1iHbdvM/LFu1ewfuqRmtxucTjh4EA4dqvva+L9Dh6CgAJrpXkVAAMTHw6RJ0L8/DBjg\n/V///ljsdmxWK839a9inw4ozL3/8+91qOMfExFDc6LxGUVERdrvda5kNGzYwceJEr/dWrlzJJ598\nwssvv+x1JN2c0tLm74+7UHZ7GE4/vE/OH+tWzf6hQ2o2DCwlJV4XWJ1zodXhc7tXeVa3WnH37Yf7\nknEtd6+ytXIQcuxksx9pX/uWln7paDWcJ0+ezAsvvEB6ejrZ2dnExMScc4S8Y8cOrr32Ws/rgwcP\nsmLFCt544w2CdW+biHQ1w8BSXtb0Od7G3atOnWp6dYsFd0wsrtRR5zbRaAji2L5+071KOl6rf5PG\njRtHSkoK6enpWCwWFi1axKpVqwgLC2Pq1KkAOJ1OoqOjPeusXLmSsrIy7rvvPs97S5YsISgoqANK\nEBF/Zzlx/Kz7eL1vJ7IVFGCpbP6I1N3Hjmt4cv0Vzd5Hu7Vx9d2r9O+XdCKL0dRJ5C7QkdMWvjwt\n0hJ/rFs1+6CTJ8+ZXu5VUkS1Y/+Z7lUnjje7ujsqynMFc7Pdq3r06MSC2s/n93UTfLnmC5rWFhHp\nMKdONd+9qqGJRjO3YgYB7ojeuPsPaLl7VUhIk+uLmJnCWUQ6xunT3k00GnWv8pz7PXas2dXdoWF1\n3au8Hg9Y10Sj96gknMERcNb1LyK+QuEsIuevpgbrkcN1IdvQNMPTRKP+ft5iZ7OrGyEhdU00UkbX\nXVzV0L2q4UKruDiM8Ijmf749DHx0qlMEFM4icjaXC2vR0XMfCdjQvaqgoNnuVVDfvapfXN3jAePi\nz72tKC4Oo3ekmmiItEDhLOJP3O4z3asajnrrbyfyTDkfPYKltrbJ1Y3AQNz94qn5zqRzulc1hK8R\npe5VIhdK4SziK9xuLMXFTdzHW+CZbrYeLsTSTPcqw2bD3S8O17e+XT/V7N1Eo7ZfPIbdDlZrJxcm\n4n8UziLdQXPdqwoLwHmEqG8OtN69KrYvrjFjGx3tej8e0B0T23r3KhHpFApnka7W0L3K6yEJbe9e\nBUBMLK6U1Ca6V9Xf3xvbF9rQRldEzEHhLNLBLCeO113N3LhXc8MRcGFbulf1wTV0eKOOVd7dq6JH\nJ1FSfroTKxKRjqZwFrkQJ09iqz+6bfxIwMb387bYvSoyktohCdTGxZ3Tq7nha6vdq4KCAIWziC9R\nOIs0p6qqiXO8je/nPdRs9yoAd3gE7v79cfWL85zbbXyOt7ZfHPTq1YkFiUh3oXAW/1Rd7d29qtE0\ns+cWo5a6V/UKrete5fV4wP5e9/Qaof73DFoRuTgUzuJ7XK4WulfVf3UWNbu60bNnXfeqkaPqp5nj\nzrnAygiP0L28ItJhFM7SvdTWerpXeR4J6DnqPQSHC+lz5AgWt7vJ1Y3gYNz94qgeftlZTTQaBW+k\nmmiISNdSOIt5uN1YnE7P7URnulc1aqJx5HCL3auIj6fm0u80mmb2Puo1oqMVvCJiegpn6RyG0XT3\nqsJGR76HC7HU1DS9us2Gu28/XOPGez0cobZx8Nrt2GMjKNcDEUSkm1M4y4UzDCylJV5NNM55TODh\nQiynm77dx9O9avQY3HH9G00zn7nQSt2rRMSfKJylZYaB5Xh5092rGi60KixosXtVbUwsrhEj64K3\niaNeda8SEfGmcPZzlooTLXavshYUYD1Z0ez67j59cA1LqmsR2UT3Kne/uPomGSIi0lYKZ19WWYnN\nsaf+aLe+e1Wjo11rQQHW4+XNru6OjMQ9aDA1Xr2az7N7lYiInDeFc3d1+nSTTyg6c3vRISgtJaqZ\n1d3hEbjj4nCN/7Z396p+cXVXOat7lYhIl1E4m1FNzVndqxqf762/xai4uNnVjZBe1MbHYx0/nlP2\nvmfdz9tf3atERExO4dzZXC6sR480273KWt+9ymIYTa5u9OhR171qREr90W487n6NmmjEx3u6V9nt\nYVTotiIRkW5H4Xwx1dZidRZ5P6GosLDR9wVYj7bQvSooCHe/OGomTj7TRKNhmrmhX7O6V4mI+DyF\nc1u53XVNNBp3r/I66q3vXuVyNbm6ERCAu18crm9P8NxO1GT3Kqu1kwsTERGzUThD3b28x46d6V7V\n1AVWRwqxVFc3vbrVWte96pJxjR4J2Og+3vj+uPvY1URDRETaxPfD2TCgpARbdu5ZF1U13Md7CNvh\nQixVVU2vbrHUda9KHdVEE41G3asCfP+PUkREOodPJkqPvy0jeNVbnvt5qaxs/pYiewyupBFnLq46\nu3tV337qXiUiIp2qTeG8ePFitm3bhsViISMjg9GjRwNw9OhRHnnkEc9yBw8e5OGHH+aaa67hscce\no7CwEJvNxpNPPsmAAQM6poImBK9ZRdBnn+KOjsaVOIzAwQM51Se20ZRzo+5VwcGdNi4REZG2aDWc\nN2/ezIEDB8jKysLhcJCRkUFWVhYAsbGxLFu2DACXy8WcOXOYMmUK7777LuHh4Tz77LNs3LiRZ599\nlv/93//t2EoaKV/+Npw+DT17AuiWIhER6VZavTR406ZNpKWlAZCYmEh5eTkVFef2Wl69ejXTpk2j\nV69ebNq0ialTpwIwadIktmzZcpGH3Qqr1RPMIiIi3U2rR87FxcWkpKR4XkdFReF0OgkNDfVabuXK\nlSxdutSzTlRU3Vleq9WKxWKhurqaoBYegBAZGUJAQMddzWy3+2dHLH+sWzX7B3+sGfyzbn+s+bwv\nCDOa6Fy1detWEhISzgnsltY5W2lp5fkOpc3s9jCcfjit7Y91q2b/4I81g3/W7cs1t/RLR6vT2jEx\nMRQ36uNcVFSE3W73WmbDhg1MnDjRax2n0wlATU0NhmG0eNQsIiIiZ7QazpMnT+aDDz4AIDs7m5iY\nmHOOkHfs2EFycrLXOuvXrwfg008/ZcKECRdzzCIiIj6t1WntcePGkZKSQnp6OhaLhUWLFrFq1SrC\nwsI8F305nU6io6M961x77bV8/vnn3HbbbQQFBfHUU091XAUiIiI+xmK05YRwJ+jIcwq+fM6iJf5Y\nt2r2D/5YM/hn3b5c8wWdcxYREZHOpXAWERExGYWziIiIySicRURETEbhLCIiYjKmuVpbRERE6ujI\nWURExGQUziIiIiajcBYRETEZhbOIiIjJKJxFRERMRuEsIiJiMq0+lcqsFi9ezLZt27BYLGRkZDB6\n9GjPZ5mZmaxduxar1UpqaioLFy7E5XKxcOFC8vPzqa2tZf78+YwfP56cnBx+/etfA5CUlMTjjz/e\nRRW17mLVPGfOHCorKwkJCQHg0UcfJTU1tavKatX51n3s2DEeffRRTp8+TU1NDQsWLGDMmDE+va+b\nq7k77evzrblBcXEx06dP58UXX2TChAk+vZ8bnF1zd9rPcP51r1q1iueff56BAwcCMGnSJH70ox91\nq3193oxu6IsvvjDuu+8+wzAMY+/evcYtt9zi+ezEiRPGVVddZdTU1BiGYRh33XWXsXXrVuOtt94y\nFi1aZBiGYeTl5Rnf+973DMMwjO9///vGtm3bDMMwjP/5n/8xNmzY0ImVtN3Frjk3N7dzC2in9tS9\ndOlSY+3atZ7177rrLsMwfHtft1Rzd9jX7am5wc9//nPjhhtuMP79738bhuHb+7lBUzV3h/1sGO2r\n++233zaeeuqpc7bVXfZ1e3TLae1NmzaRlpYGQGJiIuXl5VRUVAAQGBhIYGAglZWVuFwuTp06RURE\nBLNnz2bBggUAREVFUVZWRnV1NQUFBZ7f2q666io2bdrUNUW14mLV3N20p+677rqLWbNmAXD48GFi\nY2N9fl83VXN30p6aG9br1asXw4cPB/D5/dywXuOau5v21n227rSv26NbTmsXFxeTkpLieR0VFYXT\n6SQ0NJTg4GAeeOAB0tLSCA4OZsaMGQwZMsRr/ddff52ZM2dSWlpKeHi45/3o6GicTmen1XE+LlbN\nDf7whz9QWlpKYmIiGRkZ9OjRo9NqOR/trdvpdHL//fdz8uRJXn/9db/Y12fX3KA77Ov21FxdXc1L\nL73Eyy+/zOLFiwF8fj83VXOD7rCfoX11b926lc2bNzNv3jxcLhePPvoo0dHR3WZft0e3PHI+m9Go\nA2lFRQWvvPIK69ev5+OPP2bbtm3k5OR4Ps/MzCQ7O5sHHnigxe2Y3YXUPHfuXObPn09mZiYWi4XM\nzMxOH397tbVuu93O22+/zYIFCzyzB81tx+wupObuuq/bUvOrr77KzTff7PUPdEvbMbsLqbm77mdo\nW91jxozhJz/5CUuWLOGhhx7i0UcfbXE7vqBbHjnHxMRQXFzseV1UVITdbgfA4XAwYMAAoqKiABg/\nfjw7d+4kOTmZlStX8sknn/Dyyy8TGBh4zlTv0aNHiYmJ6dxi2uhi1QwwdepUz3amTJnC+++/34mV\nnJ/21H38+HGSkpKIiIjgiiuuYP78+T6/r5uqGbrPvm5PzRs3bsTtdpOZmUl+fj7bt2/nueee8+n9\n3FTNzz//fLfZz9C+um+66SYSExMBGDt2LCUlJURGRnabfd0e3fLIefLkyXzwwQcAZGdnExMTQ2ho\nKADx8fE4HA6qqqoA2LlzJ4MHD+bgwYOsWLGCF198keDgYKDu/EZCQgJffvklAB9++CGXXXZZF1TU\nuotVs2EY/OAHP+D48eMAfPHFFwwbNqwLKmqb9tT94Ycfsnr1agByc3Pp16+fz+/rpmruTvu6PTWv\nWLGCN998kzfffJMrr7ySRYsWkZyc7NP7uamahw4d2m32M7Sv7tdee413330XgLy8PKKioggKCuo2\n+7o9uuWR87hx40hJSSE9PR2LxcKiRYtYtWoVYWFhTJ06lXnz5jF37lxsNhtjx45l/Pjxnt+o77vv\nPs92lixZQkZGBr/61a9wu92MGTOGSZMmdWFlzbuYNd9yyy384Ac/oGfPnsTGxvKTn/ykCytrWXvq\nTkhI4LHHHuPvf/871dXVnlstfHlfN1WzxWLpNvu6PTU3x5f3c1O6036G9tXdv39/fv7zn7NixQpc\nLhdPPPEE0H32dXvokZEiIiIm0y2ntUVERHyZwllERMRkFM4iIiImo3AWERExGYWziIiIySicRURE\nTEbhLCIiYjIKZxEREZP5/wHce4xl513VPwAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ }
+ ]
+}
\ No newline at end of file
diff --git a/rajdeepmondal1.ipynb b/rajdeepmondal1.ipynb
new file mode 100644
index 0000000..0a721fb
--- /dev/null
+++ b/rajdeepmondal1.ipynb
@@ -0,0 +1,610 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "name": "First_Date_with_TensorFlow.ipynb",
+ "version": "0.3.2",
+ "provenance": []
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ }
+ },
+ "cells": [
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
\n",
+ "\n",
+ "You know what's important for understanding Deep Learning / Machine Learning?
\n",
+ "Intuition. Period.\n",
+ "\n",
+ "And Intuition comes when you run the code multiple times.\n",
+ "\n",
+ "So, today I can write a couple of defination and say this is this, this is that.
\n",
+ "You Google half of the things up. You find answers which you need to Google further.
\n",
+ "In the process, you probably won't even remember what's the first thing you started out with!\n",
+ "\n",
+ "So?\n",
+ "\n",
+ "Hence on, I will execute cells with code.
\n",
+ "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
+ "**No Theory Just Code.**\n",
+ "\n",
+ "I will at max give a defination that extends for a line. That's it.
\n",
+ "Let's get started!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "**RECOMMENDED!**
\n",
+ "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
+ "Don't just `shift+enter` the cells.\n",
+ "\n",
+ "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "gYWUpE-bYKWP",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Essential imports\n",
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "eKpz5NCIYMdi",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define some tensors\n",
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
+ " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "vmMcjzTxbWzw",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's print them out!\n",
+ "print (t1)\n",
+ "print (t2)\n",
+ "print (t3)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "10ahnfjYbcop",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Where's Waldo?
\n",
+ "I mean, the value?
\n",
+ "\n",
+ "So, the thing is you can't print the value of tensors directly.
\n",
+ "You have to use `session`, so let's do that!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ol6O5I7Tb2nb",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "sess = tf.Session()\n",
+ "print (sess.run(t1))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t2))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t3))\n",
+ "sess.close()"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "rXKfVs_zb-kU",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Aaahaa!! Just printed those tensors!!!
\n",
+ "Feels good!
\n",
+ "\n",
+ "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
+ "And you are still using the markdown cells for the theory ?!\n",
+ "\n",
+ "I am just gonna say I am a unreasonable man.
\n",
+ "\n",
+ "\n",
+ "So, you are programming with tf.
\n",
+ "What ever you do is broken down to 2 basic steps:\n",
+ "- Building the computational Graph!\n",
+ "- Execute that graph using `session`!\n",
+ "\n",
+ "That's all!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Let's compare this 2 steps with what we did above!
\n",
+ "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
+ "And then I executed each tensor in this graph using a `session`.\n",
+ "\n",
+ "That simple!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Now, let's define a few more computational graphs and execute them with sessions.\n",
+ "\n",
+ "Okay, to start with let's build this computational graph!\n",
+ "\n",
+ ""
+ ]
+ },
+ {
+ "metadata": {
+ "id": "FyVz0GNqgreZ",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the graph\n",
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "\n",
+ "# Alternatively\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "\n",
+ "# Let's execute using session\n",
+ "sess = tf.Session()\n",
+ "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
+ "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
+ "sess.close()"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "SVMMtuFYhaQB",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's define a sligtly more involved graph!\n",
+ "\n",
+ ""
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4856BTvRhiBb",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let build the graph\n",
+ "# We need to cast cause the tensors operated on should be of the same type\n",
+ "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
+ " dtype=tf.float32)\n",
+ "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
+ "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "# Let's execute\n",
+ "sess = tf.Session()\n",
+ "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', part1_res)\n",
+ "print ('Part 2 Result: ', part2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "B-_ZDtEbj4N0",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Cool! Let's go! Build another graph and execute it with sessions.
\n",
+ "\n",
+ "But this time, it's all you!\n",
+ "\n",
+ "Build this graph and execute it with `session`!\n",
+ "\n",
+ "\n",
+ "\n",
+ "_Remember that `tensors` operated on should be of the same type!_
\n",
+ "_Search up errors and other help you need on Google_"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "-uHNe1BolJY0",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "qmap38WelREN",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's do another!
\n",
+ "It's fun! Isn't it?!\n",
+ "\n",
+ "Build and execute this one!\n",
+ "\n",
+ ""
+ ]
+ },
+ {
+ "metadata": {
+ "id": "0ZhYwAlLmEvB",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "BnB0b6qCmGmg",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "And a final one, before we move on to the next part!\n",
+ "\n",
+ ""
+ ]
+ },
+ {
+ "metadata": {
+ "id": "GQWyCvsQmMcL",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "12NC7XTPsJw7",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# Linear Regression\n",
+ "\n",
+ "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
+ "\n",
+ "\n",
+ "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hW31RZkjtNwI",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Create the dataset\n",
+ "X = np.linspace(-30.0, 300.0, 300)\n",
+ "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Divide it into train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "LQKy6U33y4lt",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the hyperparameters\n",
+ "learning_rate = 0.000005\n",
+ "n_epochs = 1000\n",
+ "interval = 50"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "1h1-D8K1uT48",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# let's viz the first 10 datapoints of the dataset\n",
+ "plt.plot(train_X[:10], train_Y[:10], 'g')\n",
+ "plt.show()"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "jrsUps0nu8vj",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "** Question **
\n",
+ "Why did I created a session to plot the graph?
\n",
+ "[Ans]"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "P3-iuxE4sjAf",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the placeholders\n",
+ "\n",
+ "# Placeholders?\n",
+ "# The input to the model changes on iteration\n",
+ "# So we cannot have a constant in the input as we did before\n",
+ "# And thus we need placeholders which we can change on each \n",
+ "# iteration of the training\n",
+ "\n",
+ "x = tf.placeholder(tf.float32, name='x')\n",
+ "y = tf.placeholder(tf.float32, name='y')"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "8hPRkaoxvRyV",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the linear regression model\n",
+ "\n",
+ "# tf.Variable?\n",
+ "# We define the model parameters as tf.Variables\n",
+ "# as they get updated throghout the training.\n",
+ "# And variables denotes something which changes overtime.\n",
+ "\n",
+ "W = tf.Variable(0.0, name='weight_1')\n",
+ "b = tf.Variable(0.0, name='bias_1')\n",
+ "\n",
+ "pred_y = (W*x) + b"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "cSw1P8bkv96r",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the loss function\n",
+ "# We are going to use the mean squared loss\n",
+ "loss = tf.reduce_mean(tf.square(y - pred_y))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "5G4uQqjsygNj",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the optimizer\n",
+ "# And specify the which value (i.e. loss) it has to minimize\n",
+ "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "ttI7ZT-ozAm1",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# So the graph is now built\n",
+ "# Now let's execute the graph using session\n",
+ "# i.e. lets train the model\n",
+ "\n",
+ "# What it is to train a model?\n",
+ "# To update the paramters in the graph (i.e. tf.Variables)\n",
+ "# So that the loss is minimized\n",
+ "\n",
+ "# Okay let's start!\n",
+ "with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X[:10], test_Y[:10], 'g', label='True Function')\n",
+ " plt.plot(test_X[:10], final_preds[:10], 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "jgmH3wwt1src",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Okay, so we are doing good!
\n",
+ "\n",
+ "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
+ "\n",
+ "Or better, do it yourself!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OZ5TY7B_4E_v",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n",
+ " # YOUR CODE HERE\n",
+ " pass"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "A6MaclhK4rc6",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Okay! Now let's tweak!\n",
+ "linear_regression(learning_rate=0.000034, n_epochs=500)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "peoHmV2M40uU",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0000006, n_epochs=1000)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "KjY_KnlE5ClG",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Drive the loss to a minimum."
+ ]
+ },
+ {
+ "metadata": {
+ "id": "JKiHjGN15HPX",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# YOUR CODE HERE"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ }
+ ]
+}
\ No newline at end of file