diff --git a/AGCreates.ipynb b/AGCreates.ipynb
index 0a721fb..988230d 100644
--- a/AGCreates.ipynb
+++ b/AGCreates.ipynb
@@ -5,7 +5,8 @@
"colab": {
"name": "First_Date_with_TensorFlow.ipynb",
"version": "0.3.2",
- "provenance": []
+ "provenance": [],
+ "include_colab_link": true
},
"kernelspec": {
"name": "python3",
@@ -13,6 +14,16 @@
}
},
"cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ " "
+ ]
+ },
{
"metadata": {
"id": "2XXfXed5YLbe",
@@ -88,7 +99,11 @@
"metadata": {
"id": "vmMcjzTxbWzw",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "87cd3421-2bd4-4f14-efa0-ea5c9225e13b"
},
"cell_type": "code",
"source": [
@@ -97,8 +112,18 @@
"print (t2)\n",
"print (t3)"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 3,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_1:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_2:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -118,7 +143,11 @@
"metadata": {
"id": "ol6O5I7Tb2nb",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 204
+ },
+ "outputId": "bcb98376-cb10-4986-f5ed-ac23ace6a19a"
},
"cell_type": "code",
"source": [
@@ -130,8 +159,26 @@
"print (sess.run(t3))\n",
"sess.close()"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 4,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -177,7 +224,11 @@
"metadata": {
"id": "FyVz0GNqgreZ",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 51
+ },
+ "outputId": "a8179924-90eb-45c2-a6ab-0a6c494af463"
},
"cell_type": "code",
"source": [
@@ -193,8 +244,17 @@
"print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
"sess.close()"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 5,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -212,7 +272,11 @@
"metadata": {
"id": "4856BTvRhiBb",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "9968249b-795f-4aa7-f81a-47da4564d9f8"
},
"cell_type": "code",
"source": [
@@ -231,8 +295,18 @@
"print ('Part 2 Result: ', part2_res)\n",
"sess.close()"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 6,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -257,18 +331,43 @@
"metadata": {
"id": "-uHNe1BolJY0",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "61fa96aa-a074-4b18-91da-b422f6e7b2df"
},
"cell_type": "code",
"source": [
"# Build the graph\n",
"# YOUR CODE HERE\n",
+ "comp_graph_part_1 = tf.constant([9, 10], dtype=tf.float32) * tf.constant([7, 8.65], dtype=tf.float32)\n",
+ "comp_graph_part_1 = comp_graph_part_1 / 5.6\n",
+ "comp_graph_part_2 = tf.constant([7.65, 9], dtype=tf.float32) + tf.constant([13.5, 7.19], dtype=tf.float32)\n",
"\n",
+ "comp_graph_complete = tf.minimum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "with tf.Session() as sess:\n",
+ " part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ " print ('Complete Result: ', total_res)\n",
+ " print ('Part 1 Result: ', part1_res)\n",
+ " print ('Part 2 Result: ', part2_res)\n",
+ "# Execute \n",
"# Execute \n",
"# YOUR CODE HERE"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 7,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: [11.25 15.446429]\n",
+ "Part 1 Result: [11.25 15.446429]\n",
+ "Part 2 Result: [21.15 16.19]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -289,18 +388,58 @@
"metadata": {
"id": "0ZhYwAlLmEvB",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 153
+ },
+ "outputId": "dbfe7f3b-882c-4a8e-d9dc-8e40c9565c8c"
},
"cell_type": "code",
"source": [
"# Build the graph\n",
"# YOUR CODE HERE\n",
+ "comp_graph_part_1 = tf.constant(([7.2, 3.4],\n",
+ " [7.5, 8.6]), dtype=tf.float32)\n",
+ "comp_graph_part_1 = tf.reduce_mean(comp_graph_part_1, 1)\n",
+ "comp_graph_part_2 = tf.constant(([7, 9],\n",
+ " [8, 6]), dtype=tf.float32)\n",
+ "p1_graph = comp_graph_part_1 * comp_graph_part_2\n",
+ "\n",
+ "comp_graph_part_3 = tf.constant(([2.79, 3.81, 5.6],\n",
+ " [7.3, 5.67, 8.9]), dtype=tf.float32)\n",
+ "comp_graph_part_4 = tf.constant(([2.6, 18.1],\n",
+ " [7.86, 9.81],\n",
+ " [9.36, 10.11]), dtype=tf.float32)\n",
+ "comp_graph_part_4 = tf.transpose(comp_graph_part_4)\n",
+ "p2_graph = tf.reduce_sum(comp_graph_part_3 * comp_graph_part_4)\n",
"\n",
+ "comp_graph_complete = p1_graph + p2_graph\n",
+ "\n",
+ "with tf.Session() as sess:\n",
+ " part1_res, part2_res, total_res = sess.run([p1_graph, p2_graph, comp_graph_complete])\n",
+ " print ('Complete Result: \\n', total_res)\n",
+ " print ('Part 1 Result: \\n', part1_res)\n",
+ " print ('Part 2 Result: \\n', part2_res)\n",
"# Execute \n",
"# YOUR CODE HERE"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 8,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: \n",
+ " [[404.4483 439.7983 ]\n",
+ " [409.7483 415.64832]]\n",
+ "Part 1 Result: \n",
+ " [[37.100002 72.450005]\n",
+ " [42.4 48.300003]]\n",
+ "Part 2 Result: \n",
+ " 367.3483\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -318,18 +457,57 @@
"metadata": {
"id": "GQWyCvsQmMcL",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 170
+ },
+ "outputId": "c9161335-46db-4fc6-ccc3-3af3a064058b"
},
"cell_type": "code",
"source": [
"# Build the graph\n",
"# YOUR CODE HERE\n",
+ "t1 = tf.constant(([7.36, 8.93, 10.41],\n",
+ " [5.31, 9.38, 7.99]), dtype=tf.float32)\n",
+ "t2 = tf.constant(([7.99, 10.36],\n",
+ " [5.36, 7.98],\n",
+ " [8.91, 5.67]), dtype=tf.float32)\n",
+ "t2 = tf.transpose(t2)\n",
+ "comp_graph_part_1 = tf.reduce_sum(t1 * t2)\n",
+ "\n",
+ "comp_graph_part_2 = (tf.constant(7.0) + comp_graph_part_1) / 19.6\n",
"\n",
+ "comp_graph_tot = comp_graph_part_2 / tf.constant(([1, 5.6, 6.1, 8],\n",
+ " [0, 0, 7.98, 9],\n",
+ " [0, 0, 7.6, 7],\n",
+ " [0, 0, 0, 8.98]), dtype=tf.float32)\n",
+ "\n",
+ "with tf.Session() as sess:\n",
+ " part1_res, part2_res, total_result = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_tot])\n",
+ " print ('Total Result: \\n', total_result)\n",
+ " print ('Part 1 Result: \\n', part1_res)\n",
+ " print ('Part 2 Result: \\n', part2_res)\n",
"# Execute \n",
"# YOUR CODE HERE"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 9,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Total Result: \n",
+ " [[19.46896 3.4766 3.1916327 2.43362 ]\n",
+ " [ inf inf 2.4397192 2.1632178]\n",
+ " [ inf inf 2.5617054 2.78128 ]\n",
+ " [ inf inf inf 2.1680357]]\n",
+ "Part 1 Result: \n",
+ " 374.5916\n",
+ "Part 2 Result: \n",
+ " 19.46896\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -388,7 +566,11 @@
"metadata": {
"id": "1h1-D8K1uT48",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 347
+ },
+ "outputId": "0a4ef3ff-705b-4386-8830-9c05faa5c52c"
},
"cell_type": "code",
"source": [
@@ -396,8 +578,21 @@
"plt.plot(train_X[:10], train_Y[:10], 'g')\n",
"plt.show()"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 12,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAFKCAYAAADMuCxnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xl8TPf+P/BX9j2yjSSaFaWoLJaE\n2NeLUKVNq5deLdUraomSxhIRO6E0qiiqV1GpaFqq1tpLJFTsIiiitiSySmSZzPn9od/5Na1YJpN8\nzkxez8ejj8c4M3PmlXdHXs6Zc84YSJIkgYiIiIQyFB2AiIiIWMhERESywEImIiKSARYyERGRDLCQ\niYiIZICFTEREJAPGIl88M7NA6+u0t7dETk6R1tdbm3CG2sE5agfnWHWcoXZoa44Khc0Tl+vdFrKx\nsZHoCDqPM9QOzlE7OMeq4wy1o7rnqHeFTEREpItYyERERDLAQiYiIpIBFjIREZEMsJCJiIhkgIVM\nREQkAyxkIiIiGWAhExERyQALmYiISAZYyERERDLAQiYiInqCnOJsbL68CaXlpTXyekK/XIKIiEiO\nMooyELLtNVzKvohG9o3hV7dFtb8mC5mIiOgv7hfew8CtfXElNw0jmo+Er8K/Rl6Xu6yJiIj+dOfh\nbfT/sTeu5KZhlN9YzG6/AAYGBjXy2txCJiIiApCefxMDt/VDev4NhLWYiMmB02qsjIEqbiFnZWWh\ndevWSEpKqrA8Li4OXbt2rVIwIiKimnIj7zpe/7EP0vNvILz15BovY6CKW8gxMTFwd3evsOzBgwfY\nu3dvlUIRERHVlN9zr2LA1r64W3gHUwOnY1zLCUJyaLyFnJiYCCsrKzRq1KjC8oULF2Ls2LFVDkZE\nRFTd0rIv47Ufe+Nu4R1EB80RVsaAhoVcWlqKL774AuPHj6+wPCkpCWZmZvD19dVKOCIioupy8cEF\nvL61NzKK7mNu+xiM8hsjNM8zd1nHx8cjPj6+wrKOHTsiJCQEtra26mWlpaVYunQpli9f/twvbm9v\nCWNjoxeI+3wUChutr7O24Qy1g3PUDs6x6jjDik7fO403tvXFg0cPsCJ4BUa2Gvlcz6vOORpIkiS9\n6JMGDRoElUoFAEhPT4eDgwOio6Mxbdo01KlTBwBw8eJF9OjRA0uWLKl0PZmZBRrGrpxCYVMt661N\nOEPt4By1g3OsOs6wotMZp/DWT68jryQPS7osw7+bvPtcz9PWHCsrdY0O6oqLi1PfnjRpEgYMGICA\ngADs3r1bvbxr165PLWMiIqKaduJeEgZtfwOFZQ+xrNuXCGk8SHQkNZ6HTEREtcLxu4l4Z/sbKFY+\nworuazDg5TdFR6qgyoU8f/78Jy7fv39/VVdNRESkFUdvH8Hgn0NQqirFqp7/Q78G/UVH+gduIRMR\nkV47eGs/hu58B+WqcnzdayP+5dVbdKQnYiETEZHe+uXmbry/awgAYF3vb9HNs6fgRJXjl0sQEZFe\n2nn9Zwzd+W8YGhhiQ5/Nsi5jgIVMRER66KdrWzF897swMTTFt8Fb0Mm9i+hIz8RCJiIivZJwJR4f\n7nkP5kYW+K7fD2j3UgfRkZ4LC5mIiPTGd6nfYtQvI2BlYo3N/X5AoGsb0ZGeGwuZiIj0wsaL32Ds\n/lDYmtpiy2tb0colQHSkF8JCJiIinff1+TUYf3A0HMwd8H3/7fCr20J0pBfGQiYiIp226sxyRBz+\nGE4WCiT0/xnNnXxER9IIC5mIiHTWFylLEXl0EpwtXbD19Z1o4thUdCSN8cIgRESkkz77bRHmJs1E\nPauXkND/J9S3ayg6UpWwkImISKdIkoSFJ+Zh0cn5cLfxQEL/7fC09RIdq8pYyEREpDMkScLcpJmI\nPfUpPG29kNB/O9xtPETH0goWMhER6QRJkhB9LBIrznyO+nUaIKH/dtSzfkl0LK1hIRMRkexJkoSp\nv36CNee+RCP7xvj+tZ/gbOUiOpZWsZCJiEjWVJIKnxz6GN9cXIsmDs2w5bVtUFgqRMfSOhYyERHJ\nVrmqHB8fHINNqRvwqpMP4vtthaOFo+hY1YKFTEREsqRUKTF2fyi2pH0HP4U/vuv3A+zNHUTHqjYs\nZCIikp2y8jJ8tG8EfryagJbOrfFd3wTYmtURHatasZCJiEhWSstL8d+9w/Dz79sQ6NoWm4K3wNrU\nRnSsasdCJiIi2SgpL8EHu/+D3Td2ov1LHbG+z3ewMrESHatGsJCJiHTMsdu/4uCt/Wjk0Bh+ihao\nb9cAhga6/9UEj5SP8P6uwdif/gs6uXXBut6bYGliKTpWjWEhExHpiJLyEsxLmoXlp5dWWG5tYgNf\nhR986/rDT+EP37r+8LL1hoGBgaCkL66orAj/2fkODv9xAN09emJtrw0wNzYXHatGsZCJiHRAWvZl\njPxlOM5nnUX9Og0wtU007j68jdOZKTiTkYJjd37F0TtH1I+vY2YHH4Uf/BT+6NgwCN5mr8DdxkOW\nJf2w7CGG/PwWjt35Fb28g7G65/9gZmQmOlaNYyETEcmYJEn4+sIaRB+diuLyYgxpMhQz28+DtYl1\nhccVlObjXOZZnMk8jTOZp3A6IwVH/jiII38cxOcpSwAADuYO8FX4w6+uP3wVLeCr8EM965eElnRB\naT7e2f4mku8dR78Gr2Nl969gYmQiLI9ILGQiIpnKLMpE2IFR2HtzN+zN7LGix1cIrt/viY+1MbVF\n0EvtEfRSe/WyvJJcnM08g6tFF3H0+nGczkzBgVv7cODWPvVjnCwU6t3cfnVbwE/hX2OXpMwrycWg\n7QPx2/2TGPjym1jWbRWMDWtvLVXpJ8/KykLv3r2xbNkyBAYGoqCgAOPHj0deXh6cnZ2xePFimJqa\naisrEVGtse/mHozZH4qsR5no6NYFy7qthIuV6wuto46ZHTq4dcJARV9kNioAAGQXP8DZzDM4k5Gi\n3t39S/oe/JK+R/08FytXdUn7Kvzgq2ih9UtV5hRn462fBuBMZgreavwOYrssh5GhkVZfQ9dUqZBj\nYmLg7u6u/vOKFSvQvn17vPfee1i2bBlSU1Ph4+NT5ZBERLXFI+UjzEychq/OrYKpoSlmBM3Ff31H\nae0oagdzR3R274rO7l3Vy7IeZeFsZgpO/6Wkd93YgV03dqgf85K12192d/vDt64fHMw1u4Rl1qMs\nhGzrjwsPzmFIk6FY1DlWL44SryqNCzkxMRFWVlZo1KiRetmBAwewYcMGAMDo0aOrno6IqBY5n3UO\noXuH43JOKhrbv4IVPb7Cq07Nq/11nSyc0NWjB7p69FAvu194D2f+LOmzmaeRknEKO67/hB3Xf1I/\nxsPWC34K/8cHj/25NV3HzO6pr5VRlIE3t/VDavYlvNdsOOZ3/JRl/CeNCrm0tBRffPEFli9fjrlz\n56qXZ2VlYdOmTTh27BgaNmyIyMhI7rImInoGlaTCqrPLMTsxGqWqUgxv/iGi2s6ChbGFsEzOVi7o\nadUbPb16A3h8cNm9wrt/bkGfUm9Jb7v2A7Zd+0H9PO869f/c3f348+jmCh/YmNoCAO4V3sUbW/vh\nSm4aPvQJxax282V51LcoBpIkSU97QHx8POLj4yss69ixI9zd3dG/f39MmjQJAwYMQGBgIHx8fLBu\n3Tr4+/sjMjISTZo0weDBgytdt1JZDmPj2v2ZARHVbncK7uC9H9/D3t/3oq5VXax9bS2CGwWLjvVc\nJEnCrfxbOHnnZIX/copz1I8xgAEaOTZCq3qtkHQ7CVezryI8KBwLui9gGf/NMwv5SQYNGgSVSgUA\nSE9Ph4ODA2JjYzF69Gjs3r0bALBz504kJSUhOjq60vVkZhZolvopFAqballvbcIZagfnqB36PMef\nf/8JEw6OQXZxNrp79MRnXZejrmVdrb9OTc5QkiTczL9RYXf36cwUFJTmAwDGt5yISQHTdLKMtTVH\nheLJ1+XWaJd1XFyc+vb/bSG//PLLCAwMxPHjx9GmTRtcuHAB3t7emqUlItJjhWWFiDo6Gesv/g/m\nRuaY12ERhr06QidL6u8MDAzgVccbXnW80b/hQACPd8nfyPsdj5TFaOrYTC9+zuqg1RO+wsLCMHHi\nRCxduhROTk4YNWqUNldPRKTzTmecQugvH+Ba7lU0c2yOlT2+QmOHV0THqlaGBoaob9dQdAzZq3Ih\nz58/X33bwcEBa9eureoqiYj0TrmqHMtSPsOCE3OgVCkR6jsGU9pE1cpLRNKT1d5LohAR1ZA/Cm7h\no30fIvHOUThbumBZty/Ryb2L6FgkMyxkIqJq9OOV7zHxUBjyS/PQx7sfFndZqvEFNUi/sZCJiKpB\nQWk+Jh8Jx+bLm2BpbIklnZfh303e5QFNVCkWMhGRliXfTcKofSOQnn8Dfgp/rOixBg3sXhYdi2SO\nhUxEpCVKlRKLT8Zg8W8xkCQJYS0mIrz15Fr7dYL0YljIRERacCPvOkb9MgIn7yfjJWs3LO++Gm3r\ntRMdi3QIC5mIqAokScLmy5sw6chEFJY9xICGbyCm05JnfskC0d+xkImINJRbnIPwQ+Ox9VoCrE1s\n8EW3VXiz0ds8cIs0wkImItLA0dtH8NEvH+JO4W20dgnE8u6r4WnrJToW6TAWMhHRCygtL0VM8lx8\nnrIEhgaGiAiYinEtJsDYkL9OqWr4DiIiek5Xc64g9JcPcCYzBZ62XljRfQ1auQSIjkV6goVMRPQM\nkiRhw6V1mPbrJBQpizDolcGY2z4G1qZP/ho9Ik2wkImInuLBowcYf3A0dl3/GXXM7LCm6wq81nCA\n6Fikh1jIRESVOJC+D2P2j0RG0X20q9cBy7p9iZds3ETHIj3FQiYi+ptiZTHmHI/Gl2eXw8TQBNPa\nzsQo3zEwMjQSHY30GAuZiOgvLj24iJF7h+NS9gU0tHsZK7qvgW9df9GxqBYwFB2AiEgOJEnCmrMr\n0XNLJ1zKvoChzYZjb8hhljHVGG4hE1Gtd7/oPsbtD8X+9F/gaO6I1T3XoZd3H9GxqJZhIRNRrfbr\n7cP4cM97yHqUhc7uXfF515VwtnIRHYtqIRYyEdVaD8seYuTe4cgvycfsdvPxgc9IGBrwkzwSg+88\nIqq1Vp5ehoyi+xjdIgwf+o5iGZNQfPcRUa10v+g+lqXEwslCgdF+40THIWIhE1HttDB5HoqUhfik\n9RReApNkgYVMRLVOWvZlbLy0Dg3tXsaQpkNFxyECwEImolpo1vEolEvlmNZ2Jr82kWSDhUxEtcqx\n279i942daOMahF5ePNeY5IOFTES1hkpSYUZiJAAgOmg2DAwMBCci+v+qVMhZWVlo3bo1kpKSAAC7\nd+/G22+/jSFDhmDChAkoLS3VSkgiIm3YejUBKRmn8HrDgWjh3Ep0HKIKqlTIMTExcHd3V/959uzZ\nWLNmDTZs2ABLS0vs3bu3ygGJiLShpLwEc47PgImhCaYEThcdh+gfNC7kxMREWFlZoVGjRupldnZ2\nyM/PBwDk5+fD3t6+6gmJiLTg6/OrkV5wE8NeHQGvOt6i4xD9g4EkSdKLPqm0tBTDhg3D8uXLMXfu\nXAwYMACBgYFISkrCmDFjYGNjg6ZNm+Lzzz9/6nqUynIYG/P7RYmoeuU8ykGDpQ2gklS4NvYaHC0d\nRUci+odnHu8fHx+P+Pj4Css6duyIkJAQ2NraqpepVCrMnj0bW7Zsgbu7O8LCwrBv3z5069at0nXn\n5BRVIfqTKRQ2yMws0Pp6axPOUDs4R+3Qxhyjj0UjpzgHUW1nQVVoiszC2vX/he9F7dDWHBWKJ1+I\n5pmFHBISgpCQkArLBg0aBJVKhY0bNyI9PR1nz55FdHQ0AMDDwwMA0LZtW5w/f/6phUxEVN3S829i\nzdmVcLN2xwfN/ys6DlGlNDojPi4uTn170qRJGDBgAFq2bIm8vDxkZ2fDwcEB586dQ+vWrbUWlIhI\nE3OTZqJUVYrJgdNgbmwuOg5RpbR2iRojIyNERUVh5MiRMDU1hZubG4KDg7W1eiKiF3YmIwUJV+Lh\no/DDG43eEh2H6KmqXMjz589X3+7evTu6d+9e1VUSEVWZJEmYkTgNADC97Sx+tSLJHt+hRKSXfrm5\nG7/ePozuHj3Rwa2T6DhEz8RCJiK9o1QpMTMxCoYGhpjWdqboOETPhYVMRHpnU+oGXM5JxTuvDEET\nx6ai4xA9FxYyEemVwrJCLEieA0tjS0QETBUdh+i5sZCJSK+sOP05MoruY6TfaLhYuYqOQ/TcWMhE\npDfuF93HspRYOFkoMNpvnOg4RC+EhUxEemNh8jwUKQsR3noyrE2ffHlCIrliIRORXkjLvoyNl9ah\nod3LGNJkqOg4RC+MhUxEemH28ekol8oxre1MmBiZiI5D9MJYyESk8xLvHMWuGzvQxjUIvbz6iI5D\npBEWMhHpNJWkQvSxx6c3RQfNhoGBgeBERJphIRORTtt6NQEpGafQv8FAtHBuJToOkcZYyESks0rK\nSzAnaSZMDE0wtc100XGIqoSFTEQ66+vzq5GefwPDXh0BrzreouMQVQkLmYh0Um5xDhafjIGtaR2M\nbxUuOg5RlbGQiUgnfXbqU+SW5GJcywlwMHcUHYeoyljIRKRz0vNvYs3ZlXCzdseI5iNFxyHSChYy\nEemceUmzUKoqxeTAaTA3Nhcdh0grWMhEpFPOZKTg+yub4aPwwxuN3hIdh0hrWMhEpDMkScKMxGkA\ngOltZ8HQgL/CSH/w3UxEOuOXm7vx6+3D6ObRAx3cOomOQ6RVLGQi0glKlRIzE6NgaGCIqLazRMch\n0joWMhHphLjUjbick4p3XhmCJo5NRcch0joWMhHJXmFZIRYkz4GlsSUiAqaKjkNULVjIRCR7K05/\njvtF9zDSbzRcrFxFxyGqFixkIpK1ew/vYVlKLJwsFBjtN050HKJqY6zJkxISEhAbGwsPDw8AQFBQ\nEEJDQ5Gamoro6GgAQOPGjTFjxgytBSWi2mnGwRkoUhZietAsWJvaiI5DVG00KmQA6NOnDyIiIios\nmzNnDqZMmQIfHx9MmDABhw4dQqdOPDWBiDRzJScNq0+tRkO7lzGkyVDRcYiqldZ2WZeWluL27dvw\n8fEBAHTp0gWJiYnaWj0R1UKzEqNQLpVjWtuZMDEyER2HqFppvIWcnJyM4cOHQ6lUIiIiAo6OjrC1\ntVXf7+joiMzMTK2EJKLaJ/HOUey6sQPtPdqjl1cf0XGIqt0zCzk+Ph7x8fEVlgUHB2PMmDHo3Lkz\nUlJSEBERgTVr1lR4jCRJz3xxe3tLGBsbvWDkZ1Mo+DlTVXGG2sE5akaSJMz+MQoAsKjHItSta/uM\nZ9Cz8L2oHdU5x2cWckhICEJCQiq939/fH9nZ2bC3t0dubq56+f3791G3bt2nrjsnp+gFoj4fhcIG\nmZkFWl9vbcIZagfnqLkfr3yPE3dOoH+DgQh0C+Qcq4jvRe3Q1hwrK3WNPkNevXo1tm/fDgBIS0uD\ng4MDTE1NUb9+fZw8eRIAsGfPHnTo0EHDuERUW5WUl2B20gyYGJpgapvpouMQ1RiNPkPu168fwsPD\nERcXB6VSiTlz5gAApkyZgqioKKhUKvj6+iIoKEirYYlI/319fjXS82/gvz6j4FXHW3QcohpjID3P\nh73VpDp2oXDXTNVxhtrBOb643OIcBGz0hUqSkDzkNBzMHTlHLeAMtUOWu6yJiKpD7KnFyC3JxbiW\nE+Bg7ig6DlGNYiETkSzcKkjHmnMr4WbtjhHNR4qOQ1TjWMhEJAtzj89ESXkJJgdOg7mxueg4RDWO\nhUxEwp3JSMH3VzajuZMv3mj0lug4REKwkIlIKEmSMCNxGgBgetAsGBrw1xLVTnznE5FQ+9L34Nfb\nh9HNowc6unUWHYdIGBYyEQmjVCkxMzEKhgaGiGo7S3QcIqFYyEQkTFzqRqRmX8I7rwxBE8emouMQ\nCcVCJiIhCssKsSB5DiyMLfBJ6ymi4xAJx0ImIiFWnlmG+0X3EOo7Gq7W9UTHIRKOhUxENS6jKAPL\nUmLhZKHAaP8w0XGIZIGFTEQ1buGJeSgse4jw1pNhbcrv6SUCWMhEVMOu5KRhw8X/oaHdyxjSZKjo\nOESywUImoho16/h0lEvliGwzAyZGJqLjEMkGC5mIaszxO8ew6/rPCHRti97ewaLjEMkKC5mIaoQk\nSYg+NhUAEB00GwYGBoITEckLC5mIasTWqwk4lfEb+jcYiJbOrUXHIZIdFjIRVbuS8hLMTpoBE0MT\nTGkTJToOkSyxkImo2v3v/Bqk59/A+69+AO869UXHIZIlFjIRVau8klwsPhkDW9M6+LjVJ6LjEMkW\nC5mIqtVnv32KnJIcjGs5AQ7mjqLjEMkWC5mIqs2tgnSsObcSbtbuGNF8pOg4RLLGQiaiajP3+EyU\nlJdgUmAkzI3NRcchkjUWMhFVi7OZp/H9lc1o7uSLNxu9LToOkeyxkIlI6yRJwoxj0wAA04NmwdCA\nv2qInoV/S4hI6/al78GR24fQzaMHOrp1Fh2HSCcYa/KkhIQExMbGwsPDAwAQFBSE0NBQpKamYubM\nmTA0NIStrS0+/fRTWFhYaDUwEcmbUqXEzMQoGBoYIqrtLNFxiHSGRoUMAH369EFERESFZbNnz8ak\nSZPg4+ODBQsWICEhAYMHD65ySCLSHd+lfovU7Ev49yvvooljU9FxiHSGxoX8JCtXroS1tTUAwMHB\nAbm5udpcPRHJXGFZIeYnz4aFsQUiAqaKjkOkUzT+DDk5ORnDhw/H0KFDcfHiRQBQl3FRURG2bt2K\nXr16aSclEcleWXkZ5ifNwv2iewj1HQ1X63qiIxHpFANJkqSnPSA+Ph7x8fEVlgUHB8PT0xOdO3dG\nSkoKoqKi8NNPPwF4XMahoaHo378/Bg4c+NQXVyrLYWxsVMUfgYhEUqqUWH9mPWYfmY3fc35HPZt6\nSP0oFTZmNqKjEemUZxby82jXrh0OHz4MSZLwwQcfIDg4GCEhIc98XmZmQVVf+h8UCptqWW9twhlq\nh77PUalS4vu0zVj8Wwyu5/0OU0NTDGk6FGEtJ8LFylVrr6Pvc6wJnKF2aGuOCsWT/7Gq0WfIq1ev\nhqurK/r27Yu0tDQ4ODjAyMgIK1asQEBAwHOVMRHppnJVOX64ugWfnlyAa7lXYWJogqHNhiOsxQS8\nZOMmOh6RztKokPv164fw8HDExcVBqVRizpw5AICNGzfCzc0NiYmJAIDAwECMHj1ae2mJSBiVpMLW\nqwlYdGI+ruSmwdjQGO82fR9hLSfA3cZDdDwinadRIbu4uGD9+vX/WP7rr79WORARyYtKUmH7ta1Y\ndHI+UrMvwcjACIOb/AdhLSfC09ZLdDwivaHV056ISH+oJBV2/L4dC0/Mw6XsCzA0MMSgVwZjfMtw\neNepLzoekd5hIRNRBZIkYdeNHVh4Yh7OZ52FoYEhQhoNwoRWn6C+XUPR8Yj0FguZiAA8LuK9N3dh\n4Yn5OJOZAgMYYODLIZjYahIa2r8sOh6R3mMhE9VykiRhf/pexJyYi5SMUzCAAV5vOBATWk1CY4dX\nRMcjqjVYyES1lCRJOHhrP2JOzMFv908CAPo1eB0TW03iNaiJBGAhE9UykiThyO1DWJA8ByfuJQEA\n+nj3Q3jryWjm9KrgdES1FwuZqBY5evsIYk7MReKdowCAXl59EN56MporfAUnIyIWMlEtcPzOMcSc\nmItfbx8GAPTw/BfCW0+GX90WgpMR0f9hIRPpseS7SYg5MReH/zgAAOjq0R2ftJ6CFs6tBCcjor9j\nIRPpod/un0BM8lwcuLUPANDJrQs+CZiC1i6BgpMRUWVYyER65HTGKcQkz8Uv6XsAAB1e6oTwgClo\n49pWcDIiehYWMpEeOJt5GjHJc7Hn5i4AQFC99ogImIq29doJTkZEz4uFTKTDzmWdxcIT87Dr+s8A\ngEDXtogImIr2L3UUnIyIXhQLmUgHXXxwAQtPzMPPv28DALRyDkBEwFR0dOsMAwMDwemISBMsZCId\nkpp9CYtOzMe2az8AAFrUbYlPAqaii3s3FjGRjmMhE+mAKzlpWHRiHn68mgAJEnwV/ogImIJuHj1Z\nxER6goVMJGPXcq9g0YkF+OHqFqgkFZo7+eKTgCno6dmLRUykZ1jIRDJSVl6Gc1lnkHT3OBLv/Io9\nN3dBJanQzLE5wltPRm/vYBYxkZ5iIRMJlF+Sh5P3k5F0NxHJd5NwKuMkHikfqe9v4tAME1tPQnD9\nfjA0MBSYlIiqGwuZqIZIkoQ/Ht5C8t3jjwv4XhIuPbgACRIAwAAGeMWhKQJc2yDQtQ0CXNrA3caD\nW8REtQQLmaialKvKcS7zDJLvHVdvAd8pvK2+39zIHG3rtUOAy+MCbuUSgDpmdgITE5FILGQiLXlY\n9hCn7p9UbwGfyjiJgtIC9f1OFk7o491PvQXc3MkXpkamAhMTkZywkIk0dK/wLpLvHv9zC/g4zmed\nRblUrr6/sWNjtKobqN4C9q7TgLufiahSLGSi56CSVEjLufznrufjSLp3HOn5N9T3mxiawL9uyz+3\nftuitUsgmnh4IzOzoPKVEhH9BQuZ6AmKlcU4nXFK/fnviXtJyC3JVd9fx8wOPTz/9efWb1v41vWH\nhbGFwMREpOtYyEQAsh5l4cS9JPUW8NnM0yhVlarv97D1Qg/PXuot4Eb2jXkaEhFpFQuZah1JknA9\n7xqS1KcfHcfV3Cvq+40MjPCqk4/61KMA1zZwsXIVmJiIagONCjkhIQGxsbHw8PAAAAQFBSE0NFR9\nf1xcHFatWoX9+/drJyVRFf2eexW7buz88yCsRGQ9ylLfZ2VijU5uXRDo2hYBrm3QwrkVrE2sBaYl\notpI4y3kPn36ICIi4h/LHzx4gL1791YpFJE2pdz/Df1/7I3i8mIAgKtVPbzecODjAnZpgyaOzWBs\nyJ1FRCSW1n8LLVy4EGPHjsX48eO1vWqiF3av8C6G7vo3SspLMK/DQvT06g03a3eefkREsqNxIScn\nJ2P48OFQKpWIiIhA06ZNkZSUBDMzM/j6+j7XOuztLWFsbKRphEopFDZaX2dtow8zLFYWo+/Wd3Gv\n8C4W9liIiUETazyDPsxRDjjHquMMtaM65/jMQo6Pj0d8fHyFZcHBwRgzZgw6d+6MlJQURERE4Pvv\nv8fSpUuxfPny537xnJyiF09M8vQBAAATuUlEQVT8DAqFDc/9rCJ9mKEkSfho34dIvp2MkEaD8J+G\nH9b4z6QPc5QDzrHqOEPt0NYcKyv1ZxZySEgIQkJCKr3f398f2dnZuHTpErKysjBixAgAQEZGBsaP\nH48lS5ZoGJlIc8tOx2JL2ndo6dwKn3Zeyl3URCR7Gu2yXr16NVxdXdG3b1+kpaXBwcEBvr6+2L17\nt/oxXbt2ZRmTEHtv7MLsxOlwtaqH//X6FubG5qIjERE9k0aF3K9fP4SHhyMuLg5KpRJz5szRdi4i\njVzOTsV/9w6HmZEZ1vX+Fs5WLqIjERE9F40K2cXFBevXr3/qY3gOMtW07OIHeHfH23hYVoAve6yF\nX90WoiMRET03XvuP9EJZeRlG7H4PN/KvI6zFRAx4+U3RkYiIXggLmfRC1LHJOHL7EHp5B2NSYKTo\nOEREL4yFTDrvmwtf46tzq9DEoSmWd1vFL30gIp3E31yk0xLvHMWkIxPgYO6Ab/rEwdqUFz8gIt3E\nQiadlZ5/E8N2DQEArP3XBnjaeokNRERUBbyiPumkh2UP8e6OQXhQ/AALO32GoJfai45ERFQl3EIm\nnaOSVPjolw9xKfsC3n/1AwxtNkx0JCKiKmMhk86JSZ6Dnde3o/1LHTG73QLRcYiItIKFTDrlxyvf\nY/FvC+Fp64U1/1oHEyMT0ZGIiLSChUw642zmaYw7MArWJjZY3+c7OJg7io5ERKQ1PKiLdML9ovv4\nz453UKwsxvo+cXjFoYnoSEREWsUtZJK9kvISvLfz37hTeBtT20Sjp1dv0ZGIiLSOhUyyJkkSJh4c\nh9/un8AbL7+FMf5hoiMREVULFjLJ2oozy/Dd5W/hX7cFFnf5HAYGBqIjERFVCxYyyda+m3swM3Ea\nnC1dsK73JlgYW4iORERUbVjIJEtXctLw4d5hMDE0wbre38LFylV0JCKiasWjrEl2cotz8O6Ot1FQ\nmo8V3deghXMr0ZGIiKodt5BJVpQqJUbseQ+/513DWP+P8Uajt0RHIiKqESxkkpXoY1Nx6I8D6OnZ\nC5MDp4mOQ0RUY1jIJBsbL36DVWdX4BWHJljRYw2MDI1ERyIiqjEsZJKF43cT8cnh8bA3s8e63ptg\nY2orOhIRUY1iIZNwtwrSMWzXYKgkFdb86xt416kvOhIRUY3jUdYk1MOyh/jPjneQ9SgL8zt+ig5u\nnURHIiISglvIJIxKUmHsvlBceHAOQ5sNx7BXR4iOREQkDAuZhFl0Yj62/74VQfXaY277GNFxiIiE\nYiGTENuu/oBFJ+fDw9YLX/1rPUyMTERHIiISSqPPkBMSEhAbGwsPDw8AQFBQEEJDQ1FQUIDx48cj\nLy8Pzs7OWLx4MUxNTbUamHTfucwzGLN/JKxMrLG+dxwcLRxFRyIiEk7jg7r69OmDiIiICstWrFiB\n9u3b47333sOyZcuQmpoKHx+fKock/ZFRlIH/7HwHxcpi/K/3t2ji2FR0JCIiWdDqUdYHDhzAhg0b\nAACjR4/W5qpJD5SUl+D9XYNx++EfmBIYhd7ewaIjERHJhoEkSdKLPikhIQEbN26EnZ0dlEolIiIi\n0LRpU7Ru3RpDhw7FsWPH0LBhQ0RGRj51l7VSWQ5jY16NqTaQJAkfbPsAa0+vxaBXB+Hbgd/yu42J\niP7imYUcHx+P+Pj4CsuCg4Ph6emJzp07IyUlBVFRUfjpp5/g4+ODdevWwd/fH5GRkWjSpAkGDx5c\n6bozMwu081P8hUJhUy3rrU2qY4ZfnvkC045Ohq/CH1tf3wlLE0utrl+O+F7UDs6x6jhD7dDWHBUK\nmycuf+Yu65CQEISEhFR6v7+/P7Kzs1FeXg5XV1f4+/sDANq1a4ekpCQN45I+OZC+D9OPTUVdS2d8\n03tTrShjIqIXpdFpT6tXr8b27dsBAGlpaXBwcICRkRECAwNx/PhxAMCFCxfg7e2tvaSkk67lXsGH\ne9+HiaEJ1vX+Fq7W9URHIiKSJY0O6urXrx/Cw8MRFxcHpVKJOXPmAADCwsIwceJELF26FE5OThg1\napRWw5JuySvJxZAdbyOvJBfLun2Jls6tRUciIpItjQrZxcUF69ev/8dyBwcHrF27tsqhSPeVq8rx\n4Z73cS33Kj7yG4e3Gr8jOhIRkazxSl1ULWYkTsOBW/vQ3aMnIttEi45DRCR7LGTSurjUjVh5Zhka\n2TfGyh5fwciQp7YRET0LC5m0KvluEiYeHAc7Mzt80ycOtmZ1REciItIJLGTSmtsFf+D9XYNRLpVj\nzb++Qf06DURHIiLSGVq9dCbVXoVlhfjPzneQ+SgDc9vHoKNbZ9GRiIh0CreQqcokScK4/aNwLusM\n3m36HoY3/6/oSEREOoeFTFW2+LcYbLv2A9q4BmFeh0W8RjURkQZYyFQl269tw4LkOXC38cDaXhtg\nasTvvyYi0gQLmTR2PuscRu/7EJbGVvimdxycLJxERyIi0lk8qIs0klmUiaE730GRsghf99qIZk6v\nio5ERKTTuIVML6y0vBTDd7+LWwXpiAiYiuD6/URHIiLSeSxkeiFKlRLhh8Jw/O4x9G8wEB+3/ER0\nJCIivcBd1vTczmSk4OODY3Eu6wyaO/kitutyHlFNRKQlLGR6psKyQsQkz8WXZ7+ASlLhnVeGIDpo\nNixNLEVHIyLSGyxkeqoD6fsQfng80vNvwMvWG4s6x/IqXERE1YCFTE/04NEDTDs6CVvSvoORgRHG\n+I/HxNaTYGFsIToaEZFeYiFTBZIkYf2Z9QjbFYbs4mz4KfzxaZfP0dzJR3Q0IiK9xkImtZv5NxB+\nKAwHb+2HpbElZrabixHNQ/l9xkRENYCFTFCqlFh1dgVikuegSFmEXg17YXabhfCw9RQdjYio1mAh\n13LnMs/g44NjcSYzBY7mjvi081L8N2gYsrIeio5GRFSrsJBrqaKyIiw8MQ8rzyxDuVSOtxv/GzPa\nzYGDuSPPLSYiEoCFXAsdunUAEw+Nw838G/Cw9cKiTp+hs3tX0bGIiGo1FnItkl38ANOPTsV3l7+F\nkYERPvIbh/DWk3mBDyIiGWAh1wKSJCHhSjymHZ2ErEdZ8FH4YUnnz9Fc4Ss6GhER/YmFrOfS82/i\nk8PjsT/9F1gYWyA6aA4+9AmFsSH/1xMRyQl/K+upclU5Vp9bgflJs1GkLEInty5Y2OkzeNXxFh2N\niIieQKNCTkhIQGxsLDw8PAAAQUFBCA0Nxe7du7F27VqYmJjA2dkZ8+bNg6mpqVYD07OdzzqHCQfH\nICXjFBzMHRDTaQlCGg3i0dNERDKm8RZynz59EBERUWHZ7NmzsWPHDtjY2GDatGnYu3cvgoODqxyS\nns8j5SN8emIBvjgdi3KpHG82ehsz282Dk4WT6GhERPQMWt1lbWdnh/z8fNjY2CA/Px/29vbaXD09\nxZE/DmHioXG4nvc7PGw8EdNpCbp6dBcdi4iInpPGhZycnIzhw4dDqVQiIiICTZs2RWRkJAYMGAAb\nGxs0bdoUQUFB2sxKT5BTnI3oY5HYlLoBhgaGCPUdg08CpsDKxEp0NCIiegEGkiRJT3tAfHw84uPj\nKywLDg6Gp6cnOnfujJSUFERFRWHr1q3o378/vvjiC7i7uyMsLAyvvfYaunXrVum6lcpyGBvziws0\nIUkSvrvwHcbtGoeMwgz4ufhhdb/VaFWvlehoRESkgWduIYeEhCAkJKTS+/39/ZGdnY3s7GwAUB/o\n1bZtW5w/f/6phZyTU/SieZ9JobBBZmaB1tcrJ38U3ELE4Y+x9+ZumBuZY1rbmRjp8xFMjEy08rPX\nhhnWBM5ROzjHquMMtUNbc1QobJ643FCTla1evRrbt28HAKSlpcHBwQH29vbIy8tTF/O5c+fg6clv\nC9KmclU5Vp1ZjvabArD35m50cOuMQ4OOY4x/GEyMTETHIyKiKtDoM+R+/fohPDwccXFxUCqVmDNn\nDoyMjBAVFYWRI0fC1NQUbm5uPMJaiy4+uICPD4zGqYzfYG9mj/kdF+Htxv/mqUxERHpCo0J2cXHB\n+vXr/7G8e/fu6N6dR/ZqU7GyGItPxmDZ6c+gVCkx8OU3MavdAigsFaKjERGRFvFKXTJ29PYRTDg4\nFr/nXYObtTsWdlqCbp49RcciIqJqwEKWodziHMxInIaNl76BoYEh/uszChGBkbA2sRYdjYiIqgkL\nWUYkScJP137E5CPhyHyUgaaOr2JJ58/h79xSdDQiIqpmLGSZuF3wByYdmYDdN3bC3MgckW2iEeo7\nhkdPExHVEixkwcpV5fjfhTWYfXwGCsseov1LHbGo02eob9dQdDQiIqpBLOQalF+Sh5v5N3Aj/zpu\n5N/Ajbzr+O3+CVx8cB52ZnaI7bIcg14ZzFOZiIhqIRayFqkkFe4+vKMu3Zv513Ej7/qft28guzj7\nic8b0PANzGq/AHUt69ZwYiIikgsW8gsqKitCesFN3Mj7s3Dzr+Nm3uMCTs+/iVJV6T+eY2poCg9b\nT/jXbQmvOt7wtPWCl219eNXxhoeNJyxNLAX8JEREJCcs5L+RJAmZjzLVW7f/f2v38S7m+0X3nvg8\nezN7NHN6tULZPr7tDRcrVxgZ8ks0iIiocrWykEvLS/FHQfrjz3H/soX7fwVcpCz8x3MMDQzhZu2O\nDm6d4WX7uGy9/yxdT1sv1DGzE/CTEBGRvtDbQs4rya3w+e1ft3ZvP/wDKkn1j+dYmVjDu079x1u2\nf9nC9azjBXdrD56CRERE1UZvCrmwrBBRRyfjUu55XH1wFbkluU98nIuVKwJc2vyzdG294WThxCOc\niYhICL0p5AePsvBd6rcwMDCAh40nWrsEqsv2cfF6w8PWExbGFqKjEhER/YPeFLKHrSeujbiNes4O\neJD1z8+AiYiI5MxQdABtMjMyg6GBXv1IRERUS7C9iIiIZICFTEREJAMsZCIiIhlgIRMREckAC5mI\niEgGWMhEREQywEImIiKSARYyERGRDLCQiYiIZICFTEREJAMsZCIiIhkwkCRJEh2CiIiotuMWMhER\nkQywkImIiGSAhUxERCQDLGQiIiIZYCETERHJAAuZiIhIBoxFB9CGBw8eICIiAiUlJSgrK8PkyZPh\n6+uL1NRUREdHAwAaN26MGTNmiA0qY0qlElOnTkV6ejrKy8vxySefoFWrVti9ezfWrl0LExMTODs7\nY968eTA1NRUdV7Yqm2NBQQHGjx+PvLw8ODs7Y/HixZzjU1Q2x/8TFxeHVatWYf/+/QJTyltlM0xN\nTcXMmTNhaGgIW1tbfPrpp7CwsBAdV7aeNket94ukB9auXStt27ZNkiRJSkpKkt5//31JkiRpyJAh\n0pkzZyRJkqSPP/5YOnjwoLCMcrdlyxZp+vTpkiRJUlpamvTGG29IkiRJ7du3l/Lz8yVJkqTIyEhp\n+/btoiLqhMrmuGDBAunrr7+WJEmSPv/8c/X7kp6ssjlKkiRlZWVJw4YNk7p06SIonW6obIaDBw9W\nv//mz58vbdiwQVREnVDZHKujX/RiC/n9999X37579y6cnZ1RWlqK27dvw8fHBwDQpUsXJCYmolOn\nTqJiytprr72Gvn37AgAcHByQm5sLALCzs0N+fj5sbGyQn58Pe3t7kTFlr7I5HjhwABs2bAAAjB49\nWlg+XVHZHAFg4cKFGDt2LMaPHy8qnk6obIYrV66EtbX1P5bTkz1pjtXVL3pRyACQmZmJkSNHorCw\nEOvWrUNOTg5sbW3V9zs6OiIzM1NgQnkzMTFR3163bp36DRgZGYkBAwbAxsYGTZs2RVBQkKiIOqGy\nOWZlZWHTpk04duwYGjZsiMjISO6yforK5piUlAQzMzP4+vqKiqYzKpvh/5VxUVERtm7ditjYWCH5\ndMWT5lhd/aJzhRwfH4/4+PgKy8aMGYMOHTrg+++/x6FDhzB58mTMmzevwmMkXiFU7Wkz3LhxIy5c\nuICVK1dCpVJh9uzZ2LJlC9zd3REWFoZ9+/ahW7dugpLLy/POEQBKSkrQrl07jB49GpGRkYiPj8fg\nwYNFxJad551jaWkpli5diuXLlwtKKl8v8l4EHpdxaGgohg0bhgYNGtR0XNl63jlmZ2dXeIzW+qXK\nO71lICkpScrNzVX/OSAgQCotLZU6deqkXpaQkCDNnz9fQDrdsXnzZmnYsGFScXGxJEmSlJmZKfXt\n21d9/6ZNm6TPPvtMVDyd8fc5SpIk9ezZU317x44d6s+kqHJ/n+Pp06elnj17SiEhIVJISIjUrFkz\nKSwsTHBKeXvSe7GsrEwaOnSotHnzZoHJdMvf51hd/aIXpz3t2bMHP/zwAwDg8uXLcHV1hYmJCerX\nr4+TJ0+qH9OhQweRMWXt1q1biIuLw7Jly2BmZgYAsLe3R15envpfg+fOnYOnp6fImLL3pDkCQGBg\nII4fPw4AuHDhAry9vUVF1AlPmqOvry92796NzZs3Y/Pmzahbty6WLFkiOKl8VfZeXL16NQICAhAS\nEiIwne540hyrq1/04tuesrOzMWnSJBQWFqK0tBRTp06Fn58frl69iqioKKhUKvj6+mLy5Mmio8rW\n4sWL8fPPP6NevXrqZV999RUOHz6MVatWwdTUFG5ubpg1a1aFz1Soosrm+PDhQ0ycOBHFxcVwcnLC\n/PnzYWlpKTCpvFU2x79+7t61a1ee9vQUlc2wa9eucHNzU/89DgwM5IGGT1HZHNPT07XeL3pRyERE\nRLpOL3ZZExER6ToWMhERkQywkImIiGSAhUxERCQDLGQiIiIZYCETERHJAAuZiIhIBljIREREMvD/\nAMcReCcEeVWwAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
},
{
"metadata": {
@@ -408,7 +603,7 @@
"source": [
"** Question **
"
+ ]
+ },
{
"metadata": {
"id": "2XXfXed5YLbe",
@@ -88,7 +99,11 @@
"metadata": {
"id": "vmMcjzTxbWzw",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "87cd3421-2bd4-4f14-efa0-ea5c9225e13b"
},
"cell_type": "code",
"source": [
@@ -97,8 +112,18 @@
"print (t2)\n",
"print (t3)"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 3,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_1:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_2:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -118,7 +143,11 @@
"metadata": {
"id": "ol6O5I7Tb2nb",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 204
+ },
+ "outputId": "bcb98376-cb10-4986-f5ed-ac23ace6a19a"
},
"cell_type": "code",
"source": [
@@ -130,8 +159,26 @@
"print (sess.run(t3))\n",
"sess.close()"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 4,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -177,7 +224,11 @@
"metadata": {
"id": "FyVz0GNqgreZ",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 51
+ },
+ "outputId": "a8179924-90eb-45c2-a6ab-0a6c494af463"
},
"cell_type": "code",
"source": [
@@ -193,8 +244,17 @@
"print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
"sess.close()"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 5,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -212,7 +272,11 @@
"metadata": {
"id": "4856BTvRhiBb",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "9968249b-795f-4aa7-f81a-47da4564d9f8"
},
"cell_type": "code",
"source": [
@@ -231,8 +295,18 @@
"print ('Part 2 Result: ', part2_res)\n",
"sess.close()"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 6,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -257,18 +331,43 @@
"metadata": {
"id": "-uHNe1BolJY0",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "61fa96aa-a074-4b18-91da-b422f6e7b2df"
},
"cell_type": "code",
"source": [
"# Build the graph\n",
"# YOUR CODE HERE\n",
+ "comp_graph_part_1 = tf.constant([9, 10], dtype=tf.float32) * tf.constant([7, 8.65], dtype=tf.float32)\n",
+ "comp_graph_part_1 = comp_graph_part_1 / 5.6\n",
+ "comp_graph_part_2 = tf.constant([7.65, 9], dtype=tf.float32) + tf.constant([13.5, 7.19], dtype=tf.float32)\n",
"\n",
+ "comp_graph_complete = tf.minimum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "with tf.Session() as sess:\n",
+ " part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ " print ('Complete Result: ', total_res)\n",
+ " print ('Part 1 Result: ', part1_res)\n",
+ " print ('Part 2 Result: ', part2_res)\n",
+ "# Execute \n",
"# Execute \n",
"# YOUR CODE HERE"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 7,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: [11.25 15.446429]\n",
+ "Part 1 Result: [11.25 15.446429]\n",
+ "Part 2 Result: [21.15 16.19]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -289,18 +388,58 @@
"metadata": {
"id": "0ZhYwAlLmEvB",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 153
+ },
+ "outputId": "dbfe7f3b-882c-4a8e-d9dc-8e40c9565c8c"
},
"cell_type": "code",
"source": [
"# Build the graph\n",
"# YOUR CODE HERE\n",
+ "comp_graph_part_1 = tf.constant(([7.2, 3.4],\n",
+ " [7.5, 8.6]), dtype=tf.float32)\n",
+ "comp_graph_part_1 = tf.reduce_mean(comp_graph_part_1, 1)\n",
+ "comp_graph_part_2 = tf.constant(([7, 9],\n",
+ " [8, 6]), dtype=tf.float32)\n",
+ "p1_graph = comp_graph_part_1 * comp_graph_part_2\n",
+ "\n",
+ "comp_graph_part_3 = tf.constant(([2.79, 3.81, 5.6],\n",
+ " [7.3, 5.67, 8.9]), dtype=tf.float32)\n",
+ "comp_graph_part_4 = tf.constant(([2.6, 18.1],\n",
+ " [7.86, 9.81],\n",
+ " [9.36, 10.11]), dtype=tf.float32)\n",
+ "comp_graph_part_4 = tf.transpose(comp_graph_part_4)\n",
+ "p2_graph = tf.reduce_sum(comp_graph_part_3 * comp_graph_part_4)\n",
"\n",
+ "comp_graph_complete = p1_graph + p2_graph\n",
+ "\n",
+ "with tf.Session() as sess:\n",
+ " part1_res, part2_res, total_res = sess.run([p1_graph, p2_graph, comp_graph_complete])\n",
+ " print ('Complete Result: \\n', total_res)\n",
+ " print ('Part 1 Result: \\n', part1_res)\n",
+ " print ('Part 2 Result: \\n', part2_res)\n",
"# Execute \n",
"# YOUR CODE HERE"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 8,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: \n",
+ " [[404.4483 439.7983 ]\n",
+ " [409.7483 415.64832]]\n",
+ "Part 1 Result: \n",
+ " [[37.100002 72.450005]\n",
+ " [42.4 48.300003]]\n",
+ "Part 2 Result: \n",
+ " 367.3483\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -318,18 +457,57 @@
"metadata": {
"id": "GQWyCvsQmMcL",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 170
+ },
+ "outputId": "c9161335-46db-4fc6-ccc3-3af3a064058b"
},
"cell_type": "code",
"source": [
"# Build the graph\n",
"# YOUR CODE HERE\n",
+ "t1 = tf.constant(([7.36, 8.93, 10.41],\n",
+ " [5.31, 9.38, 7.99]), dtype=tf.float32)\n",
+ "t2 = tf.constant(([7.99, 10.36],\n",
+ " [5.36, 7.98],\n",
+ " [8.91, 5.67]), dtype=tf.float32)\n",
+ "t2 = tf.transpose(t2)\n",
+ "comp_graph_part_1 = tf.reduce_sum(t1 * t2)\n",
+ "\n",
+ "comp_graph_part_2 = (tf.constant(7.0) + comp_graph_part_1) / 19.6\n",
"\n",
+ "comp_graph_tot = comp_graph_part_2 / tf.constant(([1, 5.6, 6.1, 8],\n",
+ " [0, 0, 7.98, 9],\n",
+ " [0, 0, 7.6, 7],\n",
+ " [0, 0, 0, 8.98]), dtype=tf.float32)\n",
+ "\n",
+ "with tf.Session() as sess:\n",
+ " part1_res, part2_res, total_result = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_tot])\n",
+ " print ('Total Result: \\n', total_result)\n",
+ " print ('Part 1 Result: \\n', part1_res)\n",
+ " print ('Part 2 Result: \\n', part2_res)\n",
"# Execute \n",
"# YOUR CODE HERE"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 9,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Total Result: \n",
+ " [[19.46896 3.4766 3.1916327 2.43362 ]\n",
+ " [ inf inf 2.4397192 2.1632178]\n",
+ " [ inf inf 2.5617054 2.78128 ]\n",
+ " [ inf inf inf 2.1680357]]\n",
+ "Part 1 Result: \n",
+ " 374.5916\n",
+ "Part 2 Result: \n",
+ " 19.46896\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -388,7 +566,11 @@
"metadata": {
"id": "1h1-D8K1uT48",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 347
+ },
+ "outputId": "0a4ef3ff-705b-4386-8830-9c05faa5c52c"
},
"cell_type": "code",
"source": [
@@ -396,8 +578,21 @@
"plt.plot(train_X[:10], train_Y[:10], 'g')\n",
"plt.show()"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 12,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAFKCAYAAADMuCxnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xl8TPf+P/BX9j2yjSSaFaWoLJaE\n2NeLUKVNq5deLdUraomSxhIRO6E0qiiqV1GpaFqq1tpLJFTsIiiitiSySmSZzPn9od/5Na1YJpN8\nzkxez8ejj8c4M3PmlXdHXs6Zc84YSJIkgYiIiIQyFB2AiIiIWMhERESywEImIiKSARYyERGRDLCQ\niYiIZICFTEREJAPGIl88M7NA6+u0t7dETk6R1tdbm3CG2sE5agfnWHWcoXZoa44Khc0Tl+vdFrKx\nsZHoCDqPM9QOzlE7OMeq4wy1o7rnqHeFTEREpItYyERERDLAQiYiIpIBFjIREZEMsJCJiIhkgIVM\nREQkAyxkIiIiGWAhExERyQALmYiISAZYyERERDLAQiYiInqCnOJsbL68CaXlpTXyekK/XIKIiEiO\nMooyELLtNVzKvohG9o3hV7dFtb8mC5mIiOgv7hfew8CtfXElNw0jmo+Er8K/Rl6Xu6yJiIj+dOfh\nbfT/sTeu5KZhlN9YzG6/AAYGBjXy2txCJiIiApCefxMDt/VDev4NhLWYiMmB02qsjIEqbiFnZWWh\ndevWSEpKqrA8Li4OXbt2rVIwIiKimnIj7zpe/7EP0vNvILz15BovY6CKW8gxMTFwd3evsOzBgwfY\nu3dvlUIRERHVlN9zr2LA1r64W3gHUwOnY1zLCUJyaLyFnJiYCCsrKzRq1KjC8oULF2Ls2LFVDkZE\nRFTd0rIv47Ufe+Nu4R1EB80RVsaAhoVcWlqKL774AuPHj6+wPCkpCWZmZvD19dVKOCIioupy8cEF\nvL61NzKK7mNu+xiM8hsjNM8zd1nHx8cjPj6+wrKOHTsiJCQEtra26mWlpaVYunQpli9f/twvbm9v\nCWNjoxeI+3wUChutr7O24Qy1g3PUDs6x6jjDik7fO403tvXFg0cPsCJ4BUa2Gvlcz6vOORpIkiS9\n6JMGDRoElUoFAEhPT4eDgwOio6Mxbdo01KlTBwBw8eJF9OjRA0uWLKl0PZmZBRrGrpxCYVMt661N\nOEPt4By1g3OsOs6wotMZp/DWT68jryQPS7osw7+bvPtcz9PWHCsrdY0O6oqLi1PfnjRpEgYMGICA\ngADs3r1bvbxr165PLWMiIqKaduJeEgZtfwOFZQ+xrNuXCGk8SHQkNZ6HTEREtcLxu4l4Z/sbKFY+\nworuazDg5TdFR6qgyoU8f/78Jy7fv39/VVdNRESkFUdvH8Hgn0NQqirFqp7/Q78G/UVH+gduIRMR\nkV47eGs/hu58B+WqcnzdayP+5dVbdKQnYiETEZHe+uXmbry/awgAYF3vb9HNs6fgRJXjl0sQEZFe\n2nn9Zwzd+W8YGhhiQ5/Nsi5jgIVMRER66KdrWzF897swMTTFt8Fb0Mm9i+hIz8RCJiIivZJwJR4f\n7nkP5kYW+K7fD2j3UgfRkZ4LC5mIiPTGd6nfYtQvI2BlYo3N/X5AoGsb0ZGeGwuZiIj0wsaL32Ds\n/lDYmtpiy2tb0colQHSkF8JCJiIinff1+TUYf3A0HMwd8H3/7fCr20J0pBfGQiYiIp226sxyRBz+\nGE4WCiT0/xnNnXxER9IIC5mIiHTWFylLEXl0EpwtXbD19Z1o4thUdCSN8cIgRESkkz77bRHmJs1E\nPauXkND/J9S3ayg6UpWwkImISKdIkoSFJ+Zh0cn5cLfxQEL/7fC09RIdq8pYyEREpDMkScLcpJmI\nPfUpPG29kNB/O9xtPETH0goWMhER6QRJkhB9LBIrznyO+nUaIKH/dtSzfkl0LK1hIRMRkexJkoSp\nv36CNee+RCP7xvj+tZ/gbOUiOpZWsZCJiEjWVJIKnxz6GN9cXIsmDs2w5bVtUFgqRMfSOhYyERHJ\nVrmqHB8fHINNqRvwqpMP4vtthaOFo+hY1YKFTEREsqRUKTF2fyi2pH0HP4U/vuv3A+zNHUTHqjYs\nZCIikp2y8jJ8tG8EfryagJbOrfFd3wTYmtURHatasZCJiEhWSstL8d+9w/Dz79sQ6NoWm4K3wNrU\nRnSsasdCJiIi2SgpL8EHu/+D3Td2ov1LHbG+z3ewMrESHatGsJCJiHTMsdu/4uCt/Wjk0Bh+ihao\nb9cAhga6/9UEj5SP8P6uwdif/gs6uXXBut6bYGliKTpWjWEhExHpiJLyEsxLmoXlp5dWWG5tYgNf\nhR986/rDT+EP37r+8LL1hoGBgaCkL66orAj/2fkODv9xAN09emJtrw0wNzYXHatGsZCJiHRAWvZl\njPxlOM5nnUX9Og0wtU007j68jdOZKTiTkYJjd37F0TtH1I+vY2YHH4Uf/BT+6NgwCN5mr8DdxkOW\nJf2w7CGG/PwWjt35Fb28g7G65/9gZmQmOlaNYyETEcmYJEn4+sIaRB+diuLyYgxpMhQz28+DtYl1\nhccVlObjXOZZnMk8jTOZp3A6IwVH/jiII38cxOcpSwAADuYO8FX4w6+uP3wVLeCr8EM965eElnRB\naT7e2f4mku8dR78Gr2Nl969gYmQiLI9ILGQiIpnKLMpE2IFR2HtzN+zN7LGix1cIrt/viY+1MbVF\n0EvtEfRSe/WyvJJcnM08g6tFF3H0+nGczkzBgVv7cODWPvVjnCwU6t3cfnVbwE/hX2OXpMwrycWg\n7QPx2/2TGPjym1jWbRWMDWtvLVXpJ8/KykLv3r2xbNkyBAYGoqCgAOPHj0deXh6cnZ2xePFimJqa\naisrEVGtse/mHozZH4qsR5no6NYFy7qthIuV6wuto46ZHTq4dcJARV9kNioAAGQXP8DZzDM4k5Gi\n3t39S/oe/JK+R/08FytXdUn7Kvzgq2ih9UtV5hRn462fBuBMZgreavwOYrssh5GhkVZfQ9dUqZBj\nYmLg7u6u/vOKFSvQvn17vPfee1i2bBlSU1Ph4+NT5ZBERLXFI+UjzEychq/OrYKpoSlmBM3Ff31H\nae0oagdzR3R274rO7l3Vy7IeZeFsZgpO/6Wkd93YgV03dqgf85K12192d/vDt64fHMw1u4Rl1qMs\nhGzrjwsPzmFIk6FY1DlWL44SryqNCzkxMRFWVlZo1KiRetmBAwewYcMGAMDo0aOrno6IqBY5n3UO\noXuH43JOKhrbv4IVPb7Cq07Nq/11nSyc0NWjB7p69FAvu194D2f+LOmzmaeRknEKO67/hB3Xf1I/\nxsPWC34K/8cHj/25NV3HzO6pr5VRlIE3t/VDavYlvNdsOOZ3/JRl/CeNCrm0tBRffPEFli9fjrlz\n56qXZ2VlYdOmTTh27BgaNmyIyMhI7rImInoGlaTCqrPLMTsxGqWqUgxv/iGi2s6ChbGFsEzOVi7o\nadUbPb16A3h8cNm9wrt/bkGfUm9Jb7v2A7Zd+0H9PO869f/c3f348+jmCh/YmNoCAO4V3sUbW/vh\nSm4aPvQJxax282V51LcoBpIkSU97QHx8POLj4yss69ixI9zd3dG/f39MmjQJAwYMQGBgIHx8fLBu\n3Tr4+/sjMjISTZo0weDBgytdt1JZDmPj2v2ZARHVbncK7uC9H9/D3t/3oq5VXax9bS2CGwWLjvVc\nJEnCrfxbOHnnZIX/copz1I8xgAEaOTZCq3qtkHQ7CVezryI8KBwLui9gGf/NMwv5SQYNGgSVSgUA\nSE9Ph4ODA2JjYzF69Gjs3r0bALBz504kJSUhOjq60vVkZhZolvopFAqballvbcIZagfnqB36PMef\nf/8JEw6OQXZxNrp79MRnXZejrmVdrb9OTc5QkiTczL9RYXf36cwUFJTmAwDGt5yISQHTdLKMtTVH\nheLJ1+XWaJd1XFyc+vb/bSG//PLLCAwMxPHjx9GmTRtcuHAB3t7emqUlItJjhWWFiDo6Gesv/g/m\nRuaY12ERhr06QidL6u8MDAzgVccbXnW80b/hQACPd8nfyPsdj5TFaOrYTC9+zuqg1RO+wsLCMHHi\nRCxduhROTk4YNWqUNldPRKTzTmecQugvH+Ba7lU0c2yOlT2+QmOHV0THqlaGBoaob9dQdAzZq3Ih\nz58/X33bwcEBa9eureoqiYj0TrmqHMtSPsOCE3OgVCkR6jsGU9pE1cpLRNKT1d5LohAR1ZA/Cm7h\no30fIvHOUThbumBZty/Ryb2L6FgkMyxkIqJq9OOV7zHxUBjyS/PQx7sfFndZqvEFNUi/sZCJiKpB\nQWk+Jh8Jx+bLm2BpbIklnZfh303e5QFNVCkWMhGRliXfTcKofSOQnn8Dfgp/rOixBg3sXhYdi2SO\nhUxEpCVKlRKLT8Zg8W8xkCQJYS0mIrz15Fr7dYL0YljIRERacCPvOkb9MgIn7yfjJWs3LO++Gm3r\ntRMdi3QIC5mIqAokScLmy5sw6chEFJY9xICGbyCm05JnfskC0d+xkImINJRbnIPwQ+Ox9VoCrE1s\n8EW3VXiz0ds8cIs0wkImItLA0dtH8NEvH+JO4W20dgnE8u6r4WnrJToW6TAWMhHRCygtL0VM8lx8\nnrIEhgaGiAiYinEtJsDYkL9OqWr4DiIiek5Xc64g9JcPcCYzBZ62XljRfQ1auQSIjkV6goVMRPQM\nkiRhw6V1mPbrJBQpizDolcGY2z4G1qZP/ho9Ik2wkImInuLBowcYf3A0dl3/GXXM7LCm6wq81nCA\n6Fikh1jIRESVOJC+D2P2j0RG0X20q9cBy7p9iZds3ETHIj3FQiYi+ptiZTHmHI/Gl2eXw8TQBNPa\nzsQo3zEwMjQSHY30GAuZiOgvLj24iJF7h+NS9gU0tHsZK7qvgW9df9GxqBYwFB2AiEgOJEnCmrMr\n0XNLJ1zKvoChzYZjb8hhljHVGG4hE1Gtd7/oPsbtD8X+9F/gaO6I1T3XoZd3H9GxqJZhIRNRrfbr\n7cP4cM97yHqUhc7uXfF515VwtnIRHYtqIRYyEdVaD8seYuTe4cgvycfsdvPxgc9IGBrwkzwSg+88\nIqq1Vp5ehoyi+xjdIgwf+o5iGZNQfPcRUa10v+g+lqXEwslCgdF+40THIWIhE1HttDB5HoqUhfik\n9RReApNkgYVMRLVOWvZlbLy0Dg3tXsaQpkNFxyECwEImolpo1vEolEvlmNZ2Jr82kWSDhUxEtcqx\n279i942daOMahF5ePNeY5IOFTES1hkpSYUZiJAAgOmg2DAwMBCci+v+qVMhZWVlo3bo1kpKSAAC7\nd+/G22+/jSFDhmDChAkoLS3VSkgiIm3YejUBKRmn8HrDgWjh3Ep0HKIKqlTIMTExcHd3V/959uzZ\nWLNmDTZs2ABLS0vs3bu3ygGJiLShpLwEc47PgImhCaYEThcdh+gfNC7kxMREWFlZoVGjRupldnZ2\nyM/PBwDk5+fD3t6+6gmJiLTg6/OrkV5wE8NeHQGvOt6i4xD9g4EkSdKLPqm0tBTDhg3D8uXLMXfu\nXAwYMACBgYFISkrCmDFjYGNjg6ZNm+Lzzz9/6nqUynIYG/P7RYmoeuU8ykGDpQ2gklS4NvYaHC0d\nRUci+odnHu8fHx+P+Pj4Css6duyIkJAQ2NraqpepVCrMnj0bW7Zsgbu7O8LCwrBv3z5069at0nXn\n5BRVIfqTKRQ2yMws0Pp6axPOUDs4R+3Qxhyjj0UjpzgHUW1nQVVoiszC2vX/he9F7dDWHBWKJ1+I\n5pmFHBISgpCQkArLBg0aBJVKhY0bNyI9PR1nz55FdHQ0AMDDwwMA0LZtW5w/f/6phUxEVN3S829i\nzdmVcLN2xwfN/ys6DlGlNDojPi4uTn170qRJGDBgAFq2bIm8vDxkZ2fDwcEB586dQ+vWrbUWlIhI\nE3OTZqJUVYrJgdNgbmwuOg5RpbR2iRojIyNERUVh5MiRMDU1hZubG4KDg7W1eiKiF3YmIwUJV+Lh\no/DDG43eEh2H6KmqXMjz589X3+7evTu6d+9e1VUSEVWZJEmYkTgNADC97Sx+tSLJHt+hRKSXfrm5\nG7/ePozuHj3Rwa2T6DhEz8RCJiK9o1QpMTMxCoYGhpjWdqboOETPhYVMRHpnU+oGXM5JxTuvDEET\nx6ai4xA9FxYyEemVwrJCLEieA0tjS0QETBUdh+i5sZCJSK+sOP05MoruY6TfaLhYuYqOQ/TcWMhE\npDfuF93HspRYOFkoMNpvnOg4RC+EhUxEemNh8jwUKQsR3noyrE2ffHlCIrliIRORXkjLvoyNl9ah\nod3LGNJkqOg4RC+MhUxEemH28ekol8oxre1MmBiZiI5D9MJYyESk8xLvHMWuGzvQxjUIvbz6iI5D\npBEWMhHpNJWkQvSxx6c3RQfNhoGBgeBERJphIRORTtt6NQEpGafQv8FAtHBuJToOkcZYyESks0rK\nSzAnaSZMDE0wtc100XGIqoSFTEQ66+vzq5GefwPDXh0BrzreouMQVQkLmYh0Um5xDhafjIGtaR2M\nbxUuOg5RlbGQiUgnfXbqU+SW5GJcywlwMHcUHYeoyljIRKRz0vNvYs3ZlXCzdseI5iNFxyHSChYy\nEemceUmzUKoqxeTAaTA3Nhcdh0grWMhEpFPOZKTg+yub4aPwwxuN3hIdh0hrWMhEpDMkScKMxGkA\ngOltZ8HQgL/CSH/w3UxEOuOXm7vx6+3D6ObRAx3cOomOQ6RVLGQi0glKlRIzE6NgaGCIqLazRMch\n0joWMhHphLjUjbick4p3XhmCJo5NRcch0joWMhHJXmFZIRYkz4GlsSUiAqaKjkNULVjIRCR7K05/\njvtF9zDSbzRcrFxFxyGqFixkIpK1ew/vYVlKLJwsFBjtN050HKJqY6zJkxISEhAbGwsPDw8AQFBQ\nEEJDQ5Gamoro6GgAQOPGjTFjxgytBSWi2mnGwRkoUhZietAsWJvaiI5DVG00KmQA6NOnDyIiIios\nmzNnDqZMmQIfHx9MmDABhw4dQqdOPDWBiDRzJScNq0+tRkO7lzGkyVDRcYiqldZ2WZeWluL27dvw\n8fEBAHTp0gWJiYnaWj0R1UKzEqNQLpVjWtuZMDEyER2HqFppvIWcnJyM4cOHQ6lUIiIiAo6OjrC1\ntVXf7+joiMzMTK2EJKLaJ/HOUey6sQPtPdqjl1cf0XGIqt0zCzk+Ph7x8fEVlgUHB2PMmDHo3Lkz\nUlJSEBERgTVr1lR4jCRJz3xxe3tLGBsbvWDkZ1Mo+DlTVXGG2sE5akaSJMz+MQoAsKjHItSta/uM\nZ9Cz8L2oHdU5x2cWckhICEJCQiq939/fH9nZ2bC3t0dubq56+f3791G3bt2nrjsnp+gFoj4fhcIG\nmZkFWl9vbcIZagfnqLkfr3yPE3dOoH+DgQh0C+Qcq4jvRe3Q1hwrK3WNPkNevXo1tm/fDgBIS0uD\ng4MDTE1NUb9+fZw8eRIAsGfPHnTo0EHDuERUW5WUl2B20gyYGJpgapvpouMQ1RiNPkPu168fwsPD\nERcXB6VSiTlz5gAApkyZgqioKKhUKvj6+iIoKEirYYlI/319fjXS82/gvz6j4FXHW3QcohpjID3P\nh73VpDp2oXDXTNVxhtrBOb643OIcBGz0hUqSkDzkNBzMHTlHLeAMtUOWu6yJiKpD7KnFyC3JxbiW\nE+Bg7ig6DlGNYiETkSzcKkjHmnMr4WbtjhHNR4qOQ1TjWMhEJAtzj89ESXkJJgdOg7mxueg4RDWO\nhUxEwp3JSMH3VzajuZMv3mj0lug4REKwkIlIKEmSMCNxGgBgetAsGBrw1xLVTnznE5FQ+9L34Nfb\nh9HNowc6unUWHYdIGBYyEQmjVCkxMzEKhgaGiGo7S3QcIqFYyEQkTFzqRqRmX8I7rwxBE8emouMQ\nCcVCJiIhCssKsSB5DiyMLfBJ6ymi4xAJx0ImIiFWnlmG+0X3EOo7Gq7W9UTHIRKOhUxENS6jKAPL\nUmLhZKHAaP8w0XGIZIGFTEQ1buGJeSgse4jw1pNhbcrv6SUCWMhEVMOu5KRhw8X/oaHdyxjSZKjo\nOESywUImoho16/h0lEvliGwzAyZGJqLjEMkGC5mIaszxO8ew6/rPCHRti97ewaLjEMkKC5mIaoQk\nSYg+NhUAEB00GwYGBoITEckLC5mIasTWqwk4lfEb+jcYiJbOrUXHIZIdFjIRVbuS8hLMTpoBE0MT\nTGkTJToOkSyxkImo2v3v/Bqk59/A+69+AO869UXHIZIlFjIRVau8klwsPhkDW9M6+LjVJ6LjEMkW\nC5mIqtVnv32KnJIcjGs5AQ7mjqLjEMkWC5mIqs2tgnSsObcSbtbuGNF8pOg4RLLGQiaiajP3+EyU\nlJdgUmAkzI3NRcchkjUWMhFVi7OZp/H9lc1o7uSLNxu9LToOkeyxkIlI6yRJwoxj0wAA04NmwdCA\nv2qInoV/S4hI6/al78GR24fQzaMHOrp1Fh2HSCcYa/KkhIQExMbGwsPDAwAQFBSE0NBQpKamYubM\nmTA0NIStrS0+/fRTWFhYaDUwEcmbUqXEzMQoGBoYIqrtLNFxiHSGRoUMAH369EFERESFZbNnz8ak\nSZPg4+ODBQsWICEhAYMHD65ySCLSHd+lfovU7Ev49yvvooljU9FxiHSGxoX8JCtXroS1tTUAwMHB\nAbm5udpcPRHJXGFZIeYnz4aFsQUiAqaKjkOkUzT+DDk5ORnDhw/H0KFDcfHiRQBQl3FRURG2bt2K\nXr16aSclEcleWXkZ5ifNwv2iewj1HQ1X63qiIxHpFANJkqSnPSA+Ph7x8fEVlgUHB8PT0xOdO3dG\nSkoKoqKi8NNPPwF4XMahoaHo378/Bg4c+NQXVyrLYWxsVMUfgYhEUqqUWH9mPWYfmY3fc35HPZt6\nSP0oFTZmNqKjEemUZxby82jXrh0OHz4MSZLwwQcfIDg4GCEhIc98XmZmQVVf+h8UCptqWW9twhlq\nh77PUalS4vu0zVj8Wwyu5/0OU0NTDGk6FGEtJ8LFylVrr6Pvc6wJnKF2aGuOCsWT/7Gq0WfIq1ev\nhqurK/r27Yu0tDQ4ODjAyMgIK1asQEBAwHOVMRHppnJVOX64ugWfnlyAa7lXYWJogqHNhiOsxQS8\nZOMmOh6RztKokPv164fw8HDExcVBqVRizpw5AICNGzfCzc0NiYmJAIDAwECMHj1ae2mJSBiVpMLW\nqwlYdGI+ruSmwdjQGO82fR9hLSfA3cZDdDwinadRIbu4uGD9+vX/WP7rr79WORARyYtKUmH7ta1Y\ndHI+UrMvwcjACIOb/AdhLSfC09ZLdDwivaHV056ISH+oJBV2/L4dC0/Mw6XsCzA0MMSgVwZjfMtw\neNepLzoekd5hIRNRBZIkYdeNHVh4Yh7OZ52FoYEhQhoNwoRWn6C+XUPR8Yj0FguZiAA8LuK9N3dh\n4Yn5OJOZAgMYYODLIZjYahIa2r8sOh6R3mMhE9VykiRhf/pexJyYi5SMUzCAAV5vOBATWk1CY4dX\nRMcjqjVYyES1lCRJOHhrP2JOzMFv908CAPo1eB0TW03iNaiJBGAhE9UykiThyO1DWJA8ByfuJQEA\n+nj3Q3jryWjm9KrgdES1FwuZqBY5evsIYk7MReKdowCAXl59EN56MporfAUnIyIWMlEtcPzOMcSc\nmItfbx8GAPTw/BfCW0+GX90WgpMR0f9hIRPpseS7SYg5MReH/zgAAOjq0R2ftJ6CFs6tBCcjor9j\nIRPpod/un0BM8lwcuLUPANDJrQs+CZiC1i6BgpMRUWVYyER65HTGKcQkz8Uv6XsAAB1e6oTwgClo\n49pWcDIiehYWMpEeOJt5GjHJc7Hn5i4AQFC99ogImIq29doJTkZEz4uFTKTDzmWdxcIT87Dr+s8A\ngEDXtogImIr2L3UUnIyIXhQLmUgHXXxwAQtPzMPPv28DALRyDkBEwFR0dOsMAwMDwemISBMsZCId\nkpp9CYtOzMe2az8AAFrUbYlPAqaii3s3FjGRjmMhE+mAKzlpWHRiHn68mgAJEnwV/ogImIJuHj1Z\nxER6goVMJGPXcq9g0YkF+OHqFqgkFZo7+eKTgCno6dmLRUykZ1jIRDJSVl6Gc1lnkHT3OBLv/Io9\nN3dBJanQzLE5wltPRm/vYBYxkZ5iIRMJlF+Sh5P3k5F0NxHJd5NwKuMkHikfqe9v4tAME1tPQnD9\nfjA0MBSYlIiqGwuZqIZIkoQ/Ht5C8t3jjwv4XhIuPbgACRIAwAAGeMWhKQJc2yDQtQ0CXNrA3caD\nW8REtQQLmaialKvKcS7zDJLvHVdvAd8pvK2+39zIHG3rtUOAy+MCbuUSgDpmdgITE5FILGQiLXlY\n9hCn7p9UbwGfyjiJgtIC9f1OFk7o491PvQXc3MkXpkamAhMTkZywkIk0dK/wLpLvHv9zC/g4zmed\nRblUrr6/sWNjtKobqN4C9q7TgLufiahSLGSi56CSVEjLufznrufjSLp3HOn5N9T3mxiawL9uyz+3\nftuitUsgmnh4IzOzoPKVEhH9BQuZ6AmKlcU4nXFK/fnviXtJyC3JVd9fx8wOPTz/9efWb1v41vWH\nhbGFwMREpOtYyEQAsh5l4cS9JPUW8NnM0yhVlarv97D1Qg/PXuot4Eb2jXkaEhFpFQuZah1JknA9\n7xqS1KcfHcfV3Cvq+40MjPCqk4/61KMA1zZwsXIVmJiIagONCjkhIQGxsbHw8PAAAAQFBSE0NFR9\nf1xcHFatWoX9+/drJyVRFf2eexW7buz88yCsRGQ9ylLfZ2VijU5uXRDo2hYBrm3QwrkVrE2sBaYl\notpI4y3kPn36ICIi4h/LHzx4gL1791YpFJE2pdz/Df1/7I3i8mIAgKtVPbzecODjAnZpgyaOzWBs\nyJ1FRCSW1n8LLVy4EGPHjsX48eO1vWqiF3av8C6G7vo3SspLMK/DQvT06g03a3eefkREsqNxIScn\nJ2P48OFQKpWIiIhA06ZNkZSUBDMzM/j6+j7XOuztLWFsbKRphEopFDZaX2dtow8zLFYWo+/Wd3Gv\n8C4W9liIiUETazyDPsxRDjjHquMMtaM65/jMQo6Pj0d8fHyFZcHBwRgzZgw6d+6MlJQURERE4Pvv\nv8fSpUuxfPny537xnJyiF09M8vQBAAATuUlEQVT8DAqFDc/9rCJ9mKEkSfho34dIvp2MkEaD8J+G\nH9b4z6QPc5QDzrHqOEPt0NYcKyv1ZxZySEgIQkJCKr3f398f2dnZuHTpErKysjBixAgAQEZGBsaP\nH48lS5ZoGJlIc8tOx2JL2ndo6dwKn3Zeyl3URCR7Gu2yXr16NVxdXdG3b1+kpaXBwcEBvr6+2L17\nt/oxXbt2ZRmTEHtv7MLsxOlwtaqH//X6FubG5qIjERE9k0aF3K9fP4SHhyMuLg5KpRJz5szRdi4i\njVzOTsV/9w6HmZEZ1vX+Fs5WLqIjERE9F40K2cXFBevXr3/qY3gOMtW07OIHeHfH23hYVoAve6yF\nX90WoiMRET03XvuP9EJZeRlG7H4PN/KvI6zFRAx4+U3RkYiIXggLmfRC1LHJOHL7EHp5B2NSYKTo\nOEREL4yFTDrvmwtf46tzq9DEoSmWd1vFL30gIp3E31yk0xLvHMWkIxPgYO6Ab/rEwdqUFz8gIt3E\nQiadlZ5/E8N2DQEArP3XBnjaeokNRERUBbyiPumkh2UP8e6OQXhQ/AALO32GoJfai45ERFQl3EIm\nnaOSVPjolw9xKfsC3n/1AwxtNkx0JCKiKmMhk86JSZ6Dnde3o/1LHTG73QLRcYiItIKFTDrlxyvf\nY/FvC+Fp64U1/1oHEyMT0ZGIiLSChUw642zmaYw7MArWJjZY3+c7OJg7io5ERKQ1PKiLdML9ovv4\nz453UKwsxvo+cXjFoYnoSEREWsUtZJK9kvISvLfz37hTeBtT20Sjp1dv0ZGIiLSOhUyyJkkSJh4c\nh9/un8AbL7+FMf5hoiMREVULFjLJ2oozy/Dd5W/hX7cFFnf5HAYGBqIjERFVCxYyyda+m3swM3Ea\nnC1dsK73JlgYW4iORERUbVjIJEtXctLw4d5hMDE0wbre38LFylV0JCKiasWjrEl2cotz8O6Ot1FQ\nmo8V3deghXMr0ZGIiKodt5BJVpQqJUbseQ+/513DWP+P8Uajt0RHIiKqESxkkpXoY1Nx6I8D6OnZ\nC5MDp4mOQ0RUY1jIJBsbL36DVWdX4BWHJljRYw2MDI1ERyIiqjEsZJKF43cT8cnh8bA3s8e63ptg\nY2orOhIRUY1iIZNwtwrSMWzXYKgkFdb86xt416kvOhIRUY3jUdYk1MOyh/jPjneQ9SgL8zt+ig5u\nnURHIiISglvIJIxKUmHsvlBceHAOQ5sNx7BXR4iOREQkDAuZhFl0Yj62/74VQfXaY277GNFxiIiE\nYiGTENuu/oBFJ+fDw9YLX/1rPUyMTERHIiISSqPPkBMSEhAbGwsPDw8AQFBQEEJDQ1FQUIDx48cj\nLy8Pzs7OWLx4MUxNTbUamHTfucwzGLN/JKxMrLG+dxwcLRxFRyIiEk7jg7r69OmDiIiICstWrFiB\n9u3b47333sOyZcuQmpoKHx+fKock/ZFRlIH/7HwHxcpi/K/3t2ji2FR0JCIiWdDqUdYHDhzAhg0b\nAACjR4/W5qpJD5SUl+D9XYNx++EfmBIYhd7ewaIjERHJhoEkSdKLPikhIQEbN26EnZ0dlEolIiIi\n0LRpU7Ru3RpDhw7FsWPH0LBhQ0RGRj51l7VSWQ5jY16NqTaQJAkfbPsAa0+vxaBXB+Hbgd/yu42J\niP7imYUcHx+P+Pj4CsuCg4Ph6emJzp07IyUlBVFRUfjpp5/g4+ODdevWwd/fH5GRkWjSpAkGDx5c\n6bozMwu081P8hUJhUy3rrU2qY4ZfnvkC045Ohq/CH1tf3wlLE0utrl+O+F7UDs6x6jhD7dDWHBUK\nmycuf+Yu65CQEISEhFR6v7+/P7Kzs1FeXg5XV1f4+/sDANq1a4ekpCQN45I+OZC+D9OPTUVdS2d8\n03tTrShjIqIXpdFpT6tXr8b27dsBAGlpaXBwcICRkRECAwNx/PhxAMCFCxfg7e2tvaSkk67lXsGH\ne9+HiaEJ1vX+Fq7W9URHIiKSJY0O6urXrx/Cw8MRFxcHpVKJOXPmAADCwsIwceJELF26FE5OThg1\napRWw5JuySvJxZAdbyOvJBfLun2Jls6tRUciIpItjQrZxcUF69ev/8dyBwcHrF27tsqhSPeVq8rx\n4Z73cS33Kj7yG4e3Gr8jOhIRkazxSl1ULWYkTsOBW/vQ3aMnIttEi45DRCR7LGTSurjUjVh5Zhka\n2TfGyh5fwciQp7YRET0LC5m0KvluEiYeHAc7Mzt80ycOtmZ1REciItIJLGTSmtsFf+D9XYNRLpVj\nzb++Qf06DURHIiLSGVq9dCbVXoVlhfjPzneQ+SgDc9vHoKNbZ9GRiIh0CreQqcokScK4/aNwLusM\n3m36HoY3/6/oSEREOoeFTFW2+LcYbLv2A9q4BmFeh0W8RjURkQZYyFQl269tw4LkOXC38cDaXhtg\nasTvvyYi0gQLmTR2PuscRu/7EJbGVvimdxycLJxERyIi0lk8qIs0klmUiaE730GRsghf99qIZk6v\nio5ERKTTuIVML6y0vBTDd7+LWwXpiAiYiuD6/URHIiLSeSxkeiFKlRLhh8Jw/O4x9G8wEB+3/ER0\nJCIivcBd1vTczmSk4OODY3Eu6wyaO/kitutyHlFNRKQlLGR6psKyQsQkz8WXZ7+ASlLhnVeGIDpo\nNixNLEVHIyLSGyxkeqoD6fsQfng80vNvwMvWG4s6x/IqXERE1YCFTE/04NEDTDs6CVvSvoORgRHG\n+I/HxNaTYGFsIToaEZFeYiFTBZIkYf2Z9QjbFYbs4mz4KfzxaZfP0dzJR3Q0IiK9xkImtZv5NxB+\nKAwHb+2HpbElZrabixHNQ/l9xkRENYCFTFCqlFh1dgVikuegSFmEXg17YXabhfCw9RQdjYio1mAh\n13LnMs/g44NjcSYzBY7mjvi081L8N2gYsrIeio5GRFSrsJBrqaKyIiw8MQ8rzyxDuVSOtxv/GzPa\nzYGDuSPPLSYiEoCFXAsdunUAEw+Nw838G/Cw9cKiTp+hs3tX0bGIiGo1FnItkl38ANOPTsV3l7+F\nkYERPvIbh/DWk3mBDyIiGWAh1wKSJCHhSjymHZ2ErEdZ8FH4YUnnz9Fc4Ss6GhER/YmFrOfS82/i\nk8PjsT/9F1gYWyA6aA4+9AmFsSH/1xMRyQl/K+upclU5Vp9bgflJs1GkLEInty5Y2OkzeNXxFh2N\niIieQKNCTkhIQGxsLDw8PAAAQUFBCA0Nxe7du7F27VqYmJjA2dkZ8+bNg6mpqVYD07OdzzqHCQfH\nICXjFBzMHRDTaQlCGg3i0dNERDKm8RZynz59EBERUWHZ7NmzsWPHDtjY2GDatGnYu3cvgoODqxyS\nns8j5SN8emIBvjgdi3KpHG82ehsz282Dk4WT6GhERPQMWt1lbWdnh/z8fNjY2CA/Px/29vbaXD09\nxZE/DmHioXG4nvc7PGw8EdNpCbp6dBcdi4iInpPGhZycnIzhw4dDqVQiIiICTZs2RWRkJAYMGAAb\nGxs0bdoUQUFB2sxKT5BTnI3oY5HYlLoBhgaGCPUdg08CpsDKxEp0NCIiegEGkiRJT3tAfHw84uPj\nKywLDg6Gp6cnOnfujJSUFERFRWHr1q3o378/vvjiC7i7uyMsLAyvvfYaunXrVum6lcpyGBvziws0\nIUkSvrvwHcbtGoeMwgz4ufhhdb/VaFWvlehoRESkgWduIYeEhCAkJKTS+/39/ZGdnY3s7GwAUB/o\n1bZtW5w/f/6phZyTU/SieZ9JobBBZmaB1tcrJ38U3ELE4Y+x9+ZumBuZY1rbmRjp8xFMjEy08rPX\nhhnWBM5ROzjHquMMtUNbc1QobJ643FCTla1evRrbt28HAKSlpcHBwQH29vbIy8tTF/O5c+fg6clv\nC9KmclU5Vp1ZjvabArD35m50cOuMQ4OOY4x/GEyMTETHIyKiKtDoM+R+/fohPDwccXFxUCqVmDNn\nDoyMjBAVFYWRI0fC1NQUbm5uPMJaiy4+uICPD4zGqYzfYG9mj/kdF+Htxv/mqUxERHpCo0J2cXHB\n+vXr/7G8e/fu6N6dR/ZqU7GyGItPxmDZ6c+gVCkx8OU3MavdAigsFaKjERGRFvFKXTJ29PYRTDg4\nFr/nXYObtTsWdlqCbp49RcciIqJqwEKWodziHMxInIaNl76BoYEh/uszChGBkbA2sRYdjYiIqgkL\nWUYkScJP137E5CPhyHyUgaaOr2JJ58/h79xSdDQiIqpmLGSZuF3wByYdmYDdN3bC3MgckW2iEeo7\nhkdPExHVEixkwcpV5fjfhTWYfXwGCsseov1LHbGo02eob9dQdDQiIqpBLOQalF+Sh5v5N3Aj/zpu\n5N/Ajbzr+O3+CVx8cB52ZnaI7bIcg14ZzFOZiIhqIRayFqkkFe4+vKMu3Zv513Ej7/qft28guzj7\nic8b0PANzGq/AHUt69ZwYiIikgsW8gsqKitCesFN3Mj7s3Dzr+Nm3uMCTs+/iVJV6T+eY2poCg9b\nT/jXbQmvOt7wtPWCl219eNXxhoeNJyxNLAX8JEREJCcs5L+RJAmZjzLVW7f/f2v38S7m+0X3nvg8\nezN7NHN6tULZPr7tDRcrVxgZ8ks0iIiocrWykEvLS/FHQfrjz3H/soX7fwVcpCz8x3MMDQzhZu2O\nDm6d4WX7uGy9/yxdT1sv1DGzE/CTEBGRvtDbQs4rya3w+e1ft3ZvP/wDKkn1j+dYmVjDu079x1u2\nf9nC9azjBXdrD56CRERE1UZvCrmwrBBRRyfjUu55XH1wFbkluU98nIuVKwJc2vyzdG294WThxCOc\niYhICL0p5AePsvBd6rcwMDCAh40nWrsEqsv2cfF6w8PWExbGFqKjEhER/YPeFLKHrSeujbiNes4O\neJD1z8+AiYiI5MxQdABtMjMyg6GBXv1IRERUS7C9iIiIZICFTEREJAMsZCIiIhlgIRMREckAC5mI\niEgGWMhEREQywEImIiKSARYyERGRDLCQiYiIZICFTEREJAMsZCIiIhkwkCRJEh2CiIiotuMWMhER\nkQywkImIiGSAhUxERCQDLGQiIiIZYCETERHJAAuZiIhIBoxFB9CGBw8eICIiAiUlJSgrK8PkyZPh\n6+uL1NRUREdHAwAaN26MGTNmiA0qY0qlElOnTkV6ejrKy8vxySefoFWrVti9ezfWrl0LExMTODs7\nY968eTA1NRUdV7Yqm2NBQQHGjx+PvLw8ODs7Y/HixZzjU1Q2x/8TFxeHVatWYf/+/QJTyltlM0xN\nTcXMmTNhaGgIW1tbfPrpp7CwsBAdV7aeNket94ukB9auXStt27ZNkiRJSkpKkt5//31JkiRpyJAh\n0pkzZyRJkqSPP/5YOnjwoLCMcrdlyxZp+vTpkiRJUlpamvTGG29IkiRJ7du3l/Lz8yVJkqTIyEhp\n+/btoiLqhMrmuGDBAunrr7+WJEmSPv/8c/X7kp6ssjlKkiRlZWVJw4YNk7p06SIonW6obIaDBw9W\nv//mz58vbdiwQVREnVDZHKujX/RiC/n9999X37579y6cnZ1RWlqK27dvw8fHBwDQpUsXJCYmolOn\nTqJiytprr72Gvn37AgAcHByQm5sLALCzs0N+fj5sbGyQn58Pe3t7kTFlr7I5HjhwABs2bAAAjB49\nWlg+XVHZHAFg4cKFGDt2LMaPHy8qnk6obIYrV66EtbX1P5bTkz1pjtXVL3pRyACQmZmJkSNHorCw\nEOvWrUNOTg5sbW3V9zs6OiIzM1NgQnkzMTFR3163bp36DRgZGYkBAwbAxsYGTZs2RVBQkKiIOqGy\nOWZlZWHTpk04duwYGjZsiMjISO6yforK5piUlAQzMzP4+vqKiqYzKpvh/5VxUVERtm7ditjYWCH5\ndMWT5lhd/aJzhRwfH4/4+PgKy8aMGYMOHTrg+++/x6FDhzB58mTMmzevwmMkXiFU7Wkz3LhxIy5c\nuICVK1dCpVJh9uzZ2LJlC9zd3REWFoZ9+/ahW7dugpLLy/POEQBKSkrQrl07jB49GpGRkYiPj8fg\nwYNFxJad551jaWkpli5diuXLlwtKKl8v8l4EHpdxaGgohg0bhgYNGtR0XNl63jlmZ2dXeIzW+qXK\nO71lICkpScrNzVX/OSAgQCotLZU6deqkXpaQkCDNnz9fQDrdsXnzZmnYsGFScXGxJEmSlJmZKfXt\n21d9/6ZNm6TPPvtMVDyd8fc5SpIk9ezZU317x44d6s+kqHJ/n+Pp06elnj17SiEhIVJISIjUrFkz\nKSwsTHBKeXvSe7GsrEwaOnSotHnzZoHJdMvf51hd/aIXpz3t2bMHP/zwAwDg8uXLcHV1hYmJCerX\nr4+TJ0+qH9OhQweRMWXt1q1biIuLw7Jly2BmZgYAsLe3R15envpfg+fOnYOnp6fImLL3pDkCQGBg\nII4fPw4AuHDhAry9vUVF1AlPmqOvry92796NzZs3Y/Pmzahbty6WLFkiOKl8VfZeXL16NQICAhAS\nEiIwne540hyrq1/04tuesrOzMWnSJBQWFqK0tBRTp06Fn58frl69iqioKKhUKvj6+mLy5Mmio8rW\n4sWL8fPPP6NevXrqZV999RUOHz6MVatWwdTUFG5ubpg1a1aFz1Soosrm+PDhQ0ycOBHFxcVwcnLC\n/PnzYWlpKTCpvFU2x79+7t61a1ee9vQUlc2wa9eucHNzU/89DgwM5IGGT1HZHNPT07XeL3pRyERE\nRLpOL3ZZExER6ToWMhERkQywkImIiGSAhUxERCQDLGQiIiIZYCETERHJAAuZiIhIBljIREREMvD/\nAMcReCcEeVWwAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
},
{
"metadata": {
@@ -408,7 +603,7 @@
"source": [
"** Question **
\n",
"Why did I created a session to plot the graph?
\n",
- "[Ans]"
+ "[Ans] tf.session.run is used to evaluate a tensor. So in order to visualize the characteristics of the plot and to evaluate and find the values of the tensors we need to use session."
]
},
{
@@ -490,7 +685,11 @@
"metadata": {
"id": "ttI7ZT-ozAm1",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 721
+ },
+ "outputId": "0e560c0e-8254-4ffb-e23d-4200dad1df80"
},
"cell_type": "code",
"source": [
@@ -524,8 +723,49 @@
" plt.legend()\n",
" plt.show()"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 18,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 48241.758\n",
+ "Loss after epoch 50 is 29.843296\n",
+ "Loss after epoch 100 is 29.832943\n",
+ "Loss after epoch 150 is 29.822683\n",
+ "Loss after epoch 200 is 29.812458\n",
+ "Loss after epoch 250 is 29.802202\n",
+ "Loss after epoch 300 is 29.791937\n",
+ "Loss after epoch 350 is 29.781736\n",
+ "Loss after epoch 400 is 29.771505\n",
+ "Loss after epoch 450 is 29.761292\n",
+ "Loss after epoch 500 is 29.751057\n",
+ "Loss after epoch 550 is 29.74081\n",
+ "Loss after epoch 600 is 29.730623\n",
+ "Loss after epoch 650 is 29.72042\n",
+ "Loss after epoch 700 is 29.710188\n",
+ "Loss after epoch 750 is 29.7\n",
+ "Loss after epoch 800 is 29.689804\n",
+ "Loss after epoch 850 is 29.679585\n",
+ "Loss after epoch 900 is 29.669428\n",
+ "Loss after epoch 950 is 29.659227\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 35.69291\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeQAAAFKCAYAAADMuCxnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xd0VNXexvHv9MxMCgkEkN6rQGhS\nbIh0y/UiYgPpSBcFAgkJvQUC0hGQXkRFRCwUC4iKiBCagvTeQ0syk+nn/QNv3qsXgUCSk5n8Pmu5\nmHrmmW3Iw5xzZm+NoigKQgghhFCVVu0AQgghhJBCFkIIIXIFKWQhhBAiF5BCFkIIIXIBKWQhhBAi\nF5BCFkIIIXIBvZovfuVKarZuPzzcwvXr9mx9jUAnY5g1ZByzhozjg5MxzBr3O46RkSH/eF9Af0LW\n63VqR/B7MoZZQ8Yxa8g4PjgZw6yRHeMY0IUshBBC+AspZCGEECIXkEIWQgghcgEpZCGEECIXuKez\nrB0OB88++yy9evWiQYMGxMTE4PF40Ov1TJo0icjISKpWrUqtWrUynrN48WJ0Ojl5QAghhLgX91TI\nc+bMISwsDICpU6fStm1bWrVqxYoVK1i0aBHR0dEEBwezbNmybA0rhBBCBKq7FvKxY8c4evQojRo1\nAmD48OGYTCYAwsPD+f3337M1oBBCCJEX3LWQExISiI+PZ+3atQBYLBYAvF4vK1eupHfv3gC4XC4G\nDBjAuXPnaN68OZ06dcrG2Nlnxox3OXToINeuXcXhcFCkSFFCQ8MYN25Slmy/TZvnKFiwEFrt/x++\nnzlz3gNv98cfv6devYakpNxkwYK5REcPfeBtCiGEyDl3LOS1a9cSFRVF8eLF/3K71+slOjqa+vXr\n06BBAwCio6N5/vnn0Wg0tGvXjjp16lCtWrU7vnh4uCXbv6R+p1lRbmfUqGEArFmzhiNHjjB48OAs\nzaPTaVm8eCFWqzVLt7tmzYc0a/YURYqUZtKkCVm67cyOobg9GcesIeP44GQMs0ZWj+MdC3nLli2c\nOXOGLVu2cPHiRYxGI4ULF2bt2rWULFmSPn36ZDz21Vdfzbhcv359Dh8+fNdCzu7p2yIjQ+57es7U\nVAd2uyvj+UlJO1m1ajl2u50+fd5mwIA+fPnltwDExUXTunVbKlWqzLhxI0lNTcXr9dK//yDKlSv/\nl+16vT6Sk9Ow231/uf2ZZ57+n+3t3r0Lmy2N06dPce7cWfr1G0CDBo+yYcOXrF79IRqNhldeeR23\n282ePXvo2LEzQ4bEM3JkHAsWLCMpaSfz5s1Gr9cTGVmQmJhhfPPNRvbt28ONG9c5ffoUr73Wnmef\nfSFbxlD8PxnHrCHj+OBkDLPG/Y7jnUr8joU8derUjMszZsygaNGiJCcnYzAY6NevX8Z9x48fZ9as\nWSQmJuL1eklKSqJFixaZDvp3I7bF8fmxtff9fK1Wg8+n/OW258q+wIiGY+5re8eOHeWDD9ZgNBpv\ne/9HH31AvXoNee65Fzhx4jjTpiUyders+3qt/7h8+RKJidPZvn0bn332CTVqRLF48fssWfIBLpeb\nsWOHM2HCFN5//z0SE6dz8+aNjOcmJo7n3XdnUahQYaZMSeDrrzeg0Wg4duwo7723kLNnzzB8eOwd\nC1kIIfIiRVH45cLPpLlTaVKyeY68ZqYXl1i5ciVOp5P27dsDULZsWUaMGEHhwoVp06YNWq2Wxo0b\nU7169SwPq7Zy5cr/YxkD7N+/jxs3rrNx41cAOJ2O2z5u4MB+GceQ8+ULZ8yYhH/cZvXqUQAULFiQ\ntLQ0Tp48QYkSpTCZgjCZgpgwYcptn5eSchONRkOhQoUBqFWrDnv2JFGhQiUefrg6Op2OyMiC2Gxp\nd3/jQgiRR3h8Hr48vo7Ze6az+3ISFr2FE90uoNFosv2177mQ+/btC0Dr1q1ve/+gQYOyJtF/GdFw\nzH1/moWs3zVjMBhue7vH4/nzfj1vvz2Ihx++8z9GEhOnZ5wcd6ftAX/5LreiKGi1OhTFd7un/Y0G\nRfn/vQNutxuNRnvbbQohRF6X5k7jg4PLmLt3NqdTT6FBQ6vSz9G/9oAcKWOQmbrum0ajweFw4HA4\nOHz4EABVqjzM1q1bADhx4jirVi1/oO3dTsmSpTh9+hR2ux2n00n//r1QFAWNRovX6814XGhoKBqN\nhosXLwKwZ08SlSpVvo93KoQQgeuS7SJjt4+k5tIqDP1xMFfSL9Pp4a78/NouFrdcQVTBWnffSBZR\ndT1kf/bCC23o3r0DpUqVoWLFW0XXps3LjB07gl69uuLz+ejff+ADbe92zGYzXbr0oH//XgC8/PJr\naDQaatasRa9eXRg6dETGY6Oj4xg5cig6nY6iRYvx9NPN2LRp/f29YSGECCB/XDvInD0zWH34Q9w+\nNwXMBRj8yFA6Vu1KfnN+VTJpFBX3WWb3mX5yNuGDkzHMGjKOWUPG8cHl5TFUFIUfz21l9p7pfHv6\nawDK5StPz6i+tKnwMma9+Z63leNnWQshhBD+zu11s+7Yp8zeM4P9yXsBaFDkUXpF9aNpyeZoNbnj\n6K0UshBCiICU6kph+YGlzNs3m3NpZ9FqtPyrbGt6RvWhVqE6asf7H1LIQgghAsr5tHPM3/ceSw8s\nItWVgkVvoVu1HnSv0YuSoaXUjvePpJCFEEIEhN+S9zNnzww+Pboaj89DQUsh+tV8mzeqdiI8KELt\neHclhSyEEMJvKYrCljPfMXvPdL4/uxmAiuGV6BXVj9YVXsKkM6mc8N5JIQshhPA7Lq+LT4+sZvae\nGRy8dmsZ4MeLPkmvqL48VaJJrjlRKzOkkP/mwoXzvPHGK1SsWAm4tazk66934Mknn8r0tj755ENu\n3LjBE080YuvWLXTp8uZtH/efpRP/aSaw/3b8+FGmTJn4P0s2PvlkPapVq5FxPX/+/IwcOT7Tmf9u\nw4YN1K79KEeOHLrjexBCiJxw03mDpQcWM3/fHC7aLqDT6Ghd/iV6RfWlemSU2vEeiBTybZQoUTKj\n8FJSbtKp0+vUr98AkynovrZXvnxFypev+I/3r1q1glq16t5TIf+T4ODgLFlX+e/mzZvH3LmP3vU9\nCCFEdjqTepp5++aw/MASbO40rIZgetToQ/fqPSkWUvzuG/ADUsh3ERoaRv78Bbh69SqLFs1HrzeQ\nknKDUaMmMHHiWM6fP4fH46Fr1x7Url2XnTt3MH36ZCIi8pM/fwGKFClKUtJO1qz5iDFjJt526cQD\nB35j4MB+TJs2h3XrPuWbbzag0Wh5/PFGvPpqOy5fvkR8/BAMBgPlylW45+wXLpwnLm4wCxYsA6BL\nl/aMGZPAwoXzKFAgkkOHDnLp0kWGDRtDxYqVWLFiCVu2fItGo6VHjz788ccBDh06RGzsINq0eTnj\nPXz77dd8+OEKdDodFStWpn//gSxYMPe2S0UKIcSD2Ht5N3P2zuCzo5/iVbw8ZC3CgDqDaV+lA2Gm\nfGrHy1K5upCtI+IwfX7/yy+i1RDxt+UXnc+9gG3EvS9YceHCeVJSblKwYCHg1hzRgwcPZcOGL8mf\nvwAxMcO4ceMGb73VgyVLVjF37kzi40dTvnwFBg7sR5EiRTO2Zbfb7rh04pUrl9my5Vtmz14AQM+e\nXXjqqSasWfMhTz/djLZtX2X58sUcPXr4/sfkTy6XiylTZrJ27Wo2bPgSi8XCli3fMnfuYs6fP8fy\n5YsZMiSelSuXMm7cJJKSdv75HuzMmzeLRYtWYrFYiI5+O+O+vy8VKYUshLgfPsXHd6e/ZvaeGfx4\nbisAVfI/TK+ovrxQ7kWMun9edc+f5epCVsvp06fo06c7AEajkbi4kej1t4aqSpWqAPz22z727t3N\nvn17AHA6nbjdbi5cuED58rc+xUZF1cLpdGZs925LJx48+Dtnz56hb99bx2ntdhsXL57n5MkTPPVU\nEwBq1qzD9u3b/idzWlpaRmaAsmXL8cor7f7xPdaoUROAyMhCHDjwO4cPH6JKlYfRarUUK1acIUPi\nb/u8M2dOU6xYiYzVqmrWrM3hw38A/7tUpBBCZIbT6+STwx8xZ88MDl2/9XulUfHG9Irqx5PFnsqx\nVZfUkqsL2TZiTKY+zf5dZGQI1+5jrtH/Pob8d3q9IePPN97oTNOmLf5y/3/WOYb/Xdrwbksn6vUG\nGjR4lOjooX+5fcWKJRlLJ/7T8293DPnixQt/uX6nZR11Oi0+392nNddo/vq+PB43JpPpttsUQoh7\ncd1xjSW/L2T+vve4kn4ZvVZP24qv0qNGHx4uUE3teDnG/84LzyWqVHmYH3/8HoDr168xd+4sAAoU\niOT06ZMoisLu3bv+8py7LZ1YsWJlkpJ24XA4UBSFqVMTcTodlChRkj/+OACQsXv4XlgsVq5fv4ai\nKFy9msz582f/8bEVK1Zm//69eDwerl27SkzMrZWq/l6sxYuX5OzZ09jtNgB2706iYsUq95xJCCH+\n4+TNE8T+MIiaS6sw7pdROLwO+tTsz852+5n59Nw8VcaQyz8h52aNGzchKelXevTojNfrpXPnW7uL\nu3fvRVzcYAoXfijjuPN/3G3pxBkz5tG27av07t0NrVbLE080wmQK4qWXXiU+fghbt26mbNny95wx\nNDSUOnUeoWvXNyhXrvwdz5J+6KEiNG/eij59uqMoCm++2RuAypUr063bG/Ts2S/jPfTu/RYDBvRF\no9FSvXoUNWpEsXPnL5kaPyFE3rXr0q/M2TOTL45/hk/xUSy4OENqxPF65TcIMYaqHU81svyiuCMZ\nw6wh45g1ZBwfnFpj6FN8bDq5gdl7prP9wq3zYKpHRtErqi/PlXkBg+7+v/apBll+UQghhN9weBz8\ndG4rG06uZ+PJr7hou3VeS5MSzehVsx+PFnk84E/UygwpZCGEEFkmOT2Zb05tZOPJ9Ww+/S12z63z\nTSKCImhXuQPda/SiUkRllVPmTlLIQgghHsjR60fYcPIrNp78il8v/oLvz2+DlAkrS4vSz9CiVCvq\nFq6HTqu7y5byNilkIYQQmeLxedh5cUdGCR+7cRQArUZL3cL1aF6qFS1KtaJc+L2fhCqkkIUQQtyD\nNFcqm898x8aTX/HNqY1cc1wDwKK38kyZ52leqiVNSjangLmAykn9lxSyEEKI2zqfdo6Nf56Q9ePZ\nrbh8LgAKWx+iQ9UutCjVkkeLPkGQ/v4W3hF/JYUshBACuDUR0G9X97PhxJdsPLmefVf2ZNz3cIHq\nNC/VkhalWlE9MkrOjs4GUshCCJGHOb1Otp37kY0nv2LjyfWcS7s1o59Ba+DJYk/RonQrmpVqSfGQ\nEionDXxSyEIIkcdcd1zjm1Ob2HhyPd+d/oY0960JLsJM+XixfFtalG7FU8WfJtQUpnLSvEUKWQgh\n8oDjN4+x8cR6vju3kR9P/4hX8QJQMrQUr1d5gxalWvFI4fp+N2NWIJFCFkKIAOT1edl1aeefu6K/\n4vD1QwBo0FC7UF1alG5F81KtqBBeUY4H5xJSyEIIESBsbhvfn9nMxpNf8fWpDSSnJwNg1pszJuh4\npdaLaNMtKicVtyOFLIQQfuyi7QKbTm5g48mv2Hp2C06vE4BIc0HaVe5Ai9KteLxYI8x6863bg0O4\nki4LdORGUshCCOFnTt48wadHVrPh5JfsvpyUcXvliCo0L9WK5qVbUrNgbbQaWfLen0ghCyGEH/n0\nyGre3twHu8eOTqPj8aJP0rxUS5qVakmpsNJqxxMPQApZCCH8gMfnYcz2EczeMx2rIZjJjabzXJl/\nkS8oXO1oIotIIQshRC53zXGV7ps6s/XsZsrmK8eSFh9QIaKi2rFEFpNCFkKIXGx/8j46rX+d06mn\naF6qJbOenicTdgQoOeIvhBC51CeHP+LZNU05nXqKQXVjWNLyAynjACafkIUQIpfx+DyM/DmeuXtn\nEWIMZWnLRbQo3UrtWCKbSSELIUQukpyeTPdNHfnx3FbK56vAkpYfUC68vNqxRA6QQhZCiFxi35U9\ndFz/OmfTztCy9LPMfPo9QoyhascSOUSOIQshRC7w4R8reXZNM86lnSXmkXgWtVguZZzHyCdkIYRQ\nkdvrZvi2WN7fP5dQYxgLWyyjScnmascSKpBCFkIIlVy2X6bbpg78fP4nKoZXYknLlZTJV07tWEIl\nUshCCKGC3Zd20WlDO87bzvFsmX8xvfFsgo0hascSKpJCFkKIHPbBweVEb30bl9dFXP0R9K35tqxJ\nLKSQhRAip7i8LuJ/GsKi394nzJSPJS1X0rhEU7VjiVxCClkIIXLAJfslumxoz46L26kcUZXFLVdQ\nOqyM2rFELiKFLIQQ2WznxR103tiei7YL/Ktsa6Y2noXVYFU7lshlpJCFECIbLT+whCFbB+BRPAxr\nMJreUf3keLG4LSlkIYTIBk6vk6E/DGbpgYWEm8KZ22wRjYo3VjuWyMWkkIUQIotdtF2g84b27Ly0\ng6r5q7G45QpKhpZSO5bI5aSQhRAiC+248AudN7bjsv0Srcu/xJRGM7AYLGrHEn5AClkIIbKAoigs\nPbCI2B8G4VN8jHp0HG9W7y3Hi8U9k0IWQogH5PA4iPlhICsOLiV/UH7mNVvM48WeVDuW8DNSyEII\n8QDOp52j84Z2JF3eRfXIKBa1WE7xkBJqxxJ+SApZCCHu0/bz2+i8sT3J6Vd4qcIrJDaahllvVjuW\n8FP3tB6yw+GgSZMmrFmzhgsXLtCxY0fatWtHx44duXLlCgDr1q3jxRdf5KWXXuLjjz/O1tBCCKEm\nRVFYsH8erdc9y3XHNcY+lsDMp+dKGYsHck+FPGfOHMLCwgCYOnUqbdu2Zfny5TRt2pRFixZht9uZ\nNWsWixcvZtmyZSxZsoQbN25ka3AhhFCDw+Pgrc29iPlhIPlM+fjk+c/pVr2nnLwVYLQnjhPStweh\n7V/Osde86y7rY8eOcfToURo1agTA8OHDMZlMAISHh/P777+zd+9eqlWrRkjIraXDatWqRVJSEo0b\ny5fghRCB41zqWTpteJ09V3YTFVmTRS1WUDSkmNqxRBbSXjiPZcokglYsQePx4KrfEBQFcuAfXHf9\nhJyQkMCQIUMyrlssFnQ6HV6vl5UrV/Lcc8+RnJxMRERExmMiIiIydmULIUQg+OncDzRd/QR7ruzm\nlUqvs+7fG6WMA4jm6lWsI+KIqBeFeckCvCVKkjJvETfXfpUjZQx3+YS8du1aoqKiKF68+F9u93q9\nREdHU79+fRo0aMDnn3/+l/sVRbmnFw8Pt6DX6zIZOXMiI2XB7wclY5g1ZByzRk6Po6IoTP9lOgM2\nDUCj0TCr1Sx61vHvXdTys/hfUlJgypRb/6WmQvHiMHw4+g4dCNXfeSdyVo/jHV9ty5YtnDlzhi1b\ntnDx4kWMRiOFCxdm7dq1lCxZkj59+gBQsGBBkpOTM553+fJloqKi7vri16/bHzD+nUVGhnDlSmq2\nvkagkzHMGjKOWSOnxzHdk87ALW/x8eFVFDBHsrD5MuoXaUhyclqOZchq8rP4p/R0zAvnY5kxBe21\na/gKFMA+JI709p0gKAiup9/x6fc7jncq8TsW8tSpUzMuz5gxg6JFi5KcnIzBYKBfv34Z99WoUYO4\nuDhSUlLQ6XQkJSURGxub6aBCCJFbnEk9Tcf1r7M/eS+1C9VhYfPlPBRcRO1Y4kG5XAStXIZlykR0\nFy/gCw3DFjsMe9ceEBysarRMfw955cqVOJ1O2rdvD0DZsmUZMWIEAwYMoEuXLmg0Gnr37p1xgpcQ\nQvibH85+T7dNHbjmuEa7yh0Y/0QiJp1J7VjiQXi9mNZ8jHXiOHSnTqJYLNjfGoC9dz+UfOFqpwNA\no9zrAd9skN27TWTXzIOTMcwaMo5ZI7vHUVEU3ts7i5E/x6HT6Bj/eCJvVO2Uba+nhjz3s6goGL/6\nAmvCGPR/HEQxGEjv0Bn7WwNRChW6783m+C5rIYS4V7sv7WLA929x0XaBUGMoocZQQkxht/40hvz5\nZyihxv+/LcQYSqjp1m3/uW7RW1Q5YcrutvPOlj6sObKagpZCLGy+nEceqpfjOUQWURQM32/GOn4U\nht1JKFot6a+2wz5wCL7iuXNqUylkIcQDURSFuftmMfrn4Xh8HkqHlSHVlcr5tHM4vI5Mb0+v1RNi\nCCHEFEaIIeTPwr5V5oXCCqD3Bv1Z7KEZ9wX/57rxP9dD0Gruad4jAE6lnKTj+tf5/ep+6hR6hIUt\nllHY+lCms4vcQb/jF6zjR2H86QcAHP9qjT06Fm/5CionuzMpZCHEfbuafpW3vuvJplMbiDQXZHaT\n+TxZ/KmM+11eF6muVFJcN0l1pZDiSrl13fm3664UUl03SXGlkOJMIc2dSoozhVPpJ0lz39/u1WBD\nSEZph/zlU3rY/3+CN97afTjp1/Fcd16nQ9UujH0sAaPOmCXjI3KW7rf9WCeMxrRpAwDOJs2wx8Tj\nqVZD5WT3RgpZCHFftp/fxptfd+aC7TxPFnuKWU3mU9BS8C+PMeqM5DfnJ785/32/jtfnJc2dSqor\nFb3Vy8lLF0h13iT1z9K+VeYpf5Z+akbRpzhv3X7JdpEj1w/jVbz/+BpGrZEpjWbQrkqH+84p1KM7\ndgRLwliC1q4BwFW/IbbY4XjqN1A5WeZIIQshMsXr8zItaTITfx2HBg1D6w2nb623M7WLODN0Wh1h\npnyEmfIRGRlCYW2pTG9DURTsHjupGZ/Ib2YUdqorldqF61IponLWhxfZSnv2DJbJCQStWoHG68Vd\noya2mHjcTz2dY7NrZSUpZCHEPbtku0ivb7rxw7nvKRpcjPeaLqTeQ/XVjnVXGo0Gq8GK1WCVY8MB\nQHPlCpZpiZgXL0DjcuGpUBHbkHhczzznl0X8H1LIQoh78t3pb+jzbXeS05NpUaoV0xrPJjwo4u5P\nFCKLaG7ewDx7Opa5c9DYbXhLlMQ2KAZnm5dBl73TMOcEKWQhxB25vW4Sdoxl+u4pGLVGxj6WQNdq\nPfx6LmfhZ2w2zO+/h2XmNLQ3b+AtWAj7sFE42nUAY+CcgCeFLIT4R2dST/Pmps7svLSDUqGlmd9s\nMTUK1lQ7lsgrnE6Cli3C+m4i2iuX8YWHkxY/ivQu3cFiUTtdlpNCFkLc1lfHv+Ctzb246bxB6/Jt\nmPTkVEKMoWrHEnmBx4Pp41VYJ41Hd/YMPmswtgGDSe/ZByU0TO102UYKWQjxFw6Pg5E/x7Fg/zzM\nejPvNprJa5Xbyy5qkf18PoxffIZ1whj0R4+gmEzYe/TB3u8dlAIF1E6X7aSQhRAZjt04QvdNndmf\nvJeK4ZWY33yJfB1IZD9FwfjtJizjRmP4bR+KTkd6+07YB0TjK1JU7XQ5RgpZCAHA6sMfMuj7t7G5\n02hXuQNjHkvAYgi843QidzH8/BPWsSMx7NiOotHgeLEttkEx+MqUVTtajpNCFiKPs7ltxP4wiA/+\nWE6wIYS5TRfy7/Jt1I4lApx+726s40Zh3PwtAM4Wz2AbEoe3SlWVk6lHClmIPOzA1d/pvqkjh68f\nonpkFPOaLaJMWN77ZCJyju7QH1gTxmL64jMAXI83whYbj6d2XZWTqU8KWYg8SFEUlh1YTNyPg3F4\nHXSv3pP4BqMw6UxqRxMBSnvqJNbECZg+XoXG58Nduw62mGG4n2ikdrRcQwpZiDwmxXmTAVve4rNj\na8hnyse8ZotpUbqV2rFEgNJeuohlykSCli9B43bjqVwFW8wwXM1b+vU0l9lBClmIPGT3pV10/7oT\np1JO8kjh+rzXdAHFQoqrHUsEIM21q1hmTsO8YC6a9HQ8pctgj47F+e82oM2ehUj8nRSyEHmAoijM\n3TeL0T8Px+Pz0L/WQKIfiUWvlV8BImtp0lIxz52NefYMtKkpeB8qgn1MAo5XXgeDQe14uZr8bRQi\nwF1zXKXftz3ZdGoDkeaCzGoyj0bFG6sdSwSa9HTMixdgmT4Z7dWr+PLnJ23UONI7doWgILXT+QUp\nZCEC2Pbz23jz685csJ3niWJPMavJPApZCqkdSwQSt5ugD5ZjmZyA7sJ5fCGh2IbEkd69J0pwiNrp\n/IoUshAByOvzMi1pMhN/HYcGDbH1htGv1jtoNXLsTmQRnw/Tp6uxJoxFd/IEitmMve/b2Pu8hRIu\ny3LeDylkIQLMJdtFen3TjR/OfU/R4GLMabqA+g81UDuWCBSKgnHjeqzjR6M/+DuKwUB6527Y3x6E\nr1BhtdP5NSlkIQLId6e/oc+3b5KcfoUWpVoxrfFswoPk04rIGoatW7COG4khaReKVovjldexDRyC\nr0RJtaMFBClkIQKA2+smYcdYpu+egkFrYMyjE+hWvaes0CSyhH7nDqzjR2P84XsAnM+9gG3wULwV\nKqqcLLBIIQvh586knubNTZ3ZeWkHpUJLM7/ZYmoUrKl2LBEAdL//hjVhDKYNXwHgatwEW0w8nhry\n85UdpJCF8GNfHf+Ctzb34qbzBv8u9yKJjaYRYgxVO5bwc9rjx7BOHIfp09VoFAV3vQbYYofhbvCo\n2tECmhSyEH7I4XEw8uc4Fuyfh1lvZkqjGbxe+Q3ZRS0eiPbc2VvTXK5chsbrxV2tBvbYeFyNm8o0\nlzlAClkIP3P8xlG6berE/uS9VAyvxPzmS6gUUVntWMKPaZKTsUybjHnx+2icTjzlK2AbEofrmedl\nmsscJIUshB9ZffhDBn3/NjZ3Gu0qd2DMYwlYDBa1Ywk/pUm5iXn2DMxzZ6O1peEtXgLboBicbV4G\nvdRDTpMRF8IP2Nw2Yn8YxAd/LMdqCOa9pgtoXf4ltWMJf2W3Y14wD8uMKWhv3MAXWZDUuOE42nUE\nkyzBqRYpZCFyuYNXD9BtUwcOXz9E9cgo5jVbRJmwsmrHEv7I5YJZs4gYNRrd5Uv48uUjLW4k6V26\ng9Wqdro8TwpZiFxKURSWHVhM3I+DcXgddKvWg2ENR2PSyScYkUleL6aPV2FNnACnT6G1WLG9M4j0\nnn1RwvKpnU78SQpZiFzobOoZRmyLY92xT8lnysfcZotoWfoZtWMJf6MoGL9YhzVhDPrDh1CMRujf\nn6vd+qJERqqdTvyNFLIQucgl+yWm7Upk6e+LcPlc1C1cj7lNF1IspLja0YQ/URQMm7/BOn4Mhr27\nUXQ60tt3xP5ONPmjKqNcSVVNV4kMAAAgAElEQVQ7obgNKWQhcoHrjmvM3D2NBfvnYvfYKRFSkoF1\nh/BShVfQaXVqxxN+RL/9Z6zjRmLcvg0AR+s22KNj8ZYpp3IycTdSyEKoKNWVwnt7Z/He3lmkulIo\nbH2IEQ3H8lrl9hh1RrXjCT+i37cHy/jRmL79GgBn85bYBsfhfbiaysnEvZJCFkIFdredhb/NZ+bu\nd7nmuEb+oPyMbDiOjg93waw3qx1P+BHdkcNYEsYStO5TAFyPPo4tdhieuvVUTiYySwpZiBzk9DpZ\nfmAx7+5K5LL9EqHGMGIeiadb9R4EG0PUjif8iPbMaSyJEwj6cCUanw93rdrYYobhfqKRTHPpp6SQ\nhcgBHp+HlQeXkfjrBM6mncGit9K/1kB6RfUlX1C42vGEH9FcuoR16iSCli5C43bjqVQZW8wwXC1a\nSRH7OSlkIbKRT/Hx2dE1TP5wAoevHsakM/Fmjd70q/kOkRb52om4d5rr17DMmo55/hw06el4S5bC\nNngozn+3AZ2c+BcIpJCFyAaKorDh5FdM+GUMB6/9jl6r540qnXmnziCKBBdVO57wJ2lpWObPwTxr\nOtqUm3gLP4R91Hgcr7UHg0HtdCILSSELkYUUReH7s5uZ8Mtoki7vQqvR0rbiq4xvPoYQj3wiFpng\ncGBeuhDL1ES0ycn4IiJIGzGW9E5dwSwn/gUiKWQhssj2Cz8z/pdR/Hz+JwCeK/sC0XVjqRhRicjw\nEK7IZAziXng8BH24EkviBHTnzuILDsEWHUv6m71QQkLVTieykRSyEA9o7+XdjN8xmu9OfwNA05LN\nGfJIHNUia6icTPgVnw/TZ2uwJIxFf/wYSlAQ9t5vYe/bHyUiv9rpRA6QQhbiPv1x7SAJO8by5fF1\nADxW9AmGPBLPIw/J9z9FJigKxq83YB03Gv2B31D0etI7dsH+TjS+wg+pnU7kIClkITLp+M1jTNox\nnjVHPkZBoXahOsTUG8YTxRqpHU34GcNPP2AdOxLDzh0oGg2Ol17BNigGX6nSakcTKpBCFuIenUs9\ny5RdE1l5cBlexUvV/NWIqRdH05It0Mj3P0Um6HfvwjpuFMbvNwPgfOZ5bIOH4q1UWeVkQk1SyELc\nxWX7ZabtSmTJ7wtx+VyUy1eewY8M5bmyL6DVaNWOJ/yI7uABrBPGYFr/BQCuRo2xxcTjqVlb5WQi\nN5BCFuIfXHdcY9bu6by//72/rMDUpsLL6LXyV0fcO+2J41gnjcf0yUdoFAV33XrYYofhfvRxtaOJ\nXER+qwjxN6muFObunc2cvTMzVmAa3nAMr1d+Q1ZgEpmivXAey5RJBK1YgsbjwVO1GrbYeFxNmss0\nl+J/SCEL8ad0TzoL989nxu4psgKTeCCaq1exzHgX88J5aBwOPGXLYR8Sh/O5F0ArhznE7UkhizzP\n5XWx7MBipu5K5JL9IqHGMIY8Ekf36j1lBSaRKZrUFMxzZmJ+bxbatFS8RYthHxSDo+2roJdft+LO\n5CdE5Fken4ePD60icecEzqSelhWYxP1LT8e8cD6WGVPQXruGr0AkaTFxpL/RGUwmtdMJPyGFLPIc\nn+Jj3dFPmfjrOI7eOHJrBabqvehXa4CswCQyx+UiaOUyLFMmort4AV9oGLbYYdi79oDgYLXTCT8j\nhSzyDEVR2HhyPRN2jOHA1d/Qa/W0r9KJAXWiZQUmkTleL6Y1H2OdOA7dqZMoFgv2twZg790PJZ/s\nXRH3554K2eFw8Oyzz9KrVy9at27N0qVLSUhIYMeOHVitVgCqVq1KrVq1Mp6zePFidLJGp8glfjj7\nPWO3jyDp8i40aHipwisMrDuE0mFl1I4m/ImiYPzqC6wJY9D/cRDFaMTerQf2fgNQChVSO53wc/dU\nyHPmzCEsLAyAtWvXcvXqVQoWLPiXxwQHB7Ns2bKsTyjEA/r0yGre/Loz8NcVmIS4Z4qC4fvNWMeP\nwrA7CUWrJf219tgHDMZXvITa6USAuGshHzt2jKNHj9KoUSMAmjRpQnBwMJ9//nl2ZxPigR29foR3\ntvTDaghm9fOfUbtQXbUjCT+j3/EL1vGjMP70AwCOf7XGHh2Lt3wFlZOJQHPXL8QlJCQwZMiQjOvB\n/3CigsvlYsCAAbzyyissWrQo6xIKcZ/SPel03dQBmzuNdxvNkDIWmaL7bT+h7doS/mxTjD/9gLNJ\nM65/+wOp8xdLGYtsccdPyGvXriUqKorixYvfdUPR0dE8//zzaDQa2rVrR506dahWrdodnxMebkGv\nz97jzJGR8j3SB+WvY9ht3TscuPobPev0pFvDjmrH8dtxzG2yfRwPH4bhw2HVqlvXn3gCxo3D9Oij\nBMoXmORnMWtk9TjesZC3bNnCmTNn2LJlCxcvXsRoNFK4cGEaNmz4P4999dVXMy7Xr1+fw4cP37WQ\nr1+332fsexMZGcKVK6nZ+hqBzl/H8ONDq3h/9/tUK1CDmFojVX8P/jqOuU12jqP23FkskxMI+mA5\nGq8Xd42at+abbtT41jSXAfL/T34Ws8b9juOdSvyOhTx16tSMyzNmzKBo0aK3LePjx48za9YsEhMT\n8Xq9JCUl0aJFi0wHFSIrHL52iEHf9yfEGMr7zZcQpA9SO5LIxTRXrmCZPhnzovfRuFx4KlTENiQe\n1zPPyXzTIkdl+nvIc+bMYdu2bVy5coVu3boRFRVFdHQ0hQsXpk2bNmi1Who3bkz16tWzI68Qd2Rz\n2+i66Q3sHjsLmi+TrzWJf6S5eQPz7OlY5s5BY7fhLVES26AYnG1eBvnKplCBRlEURa0Xz+7dJrJr\n5sH52xj2+64nq/5YQddqbzLu8Ulqx8ngb+OYW2XJONpsmBfMxTJjKtqbN/AWLIT97UE42ncEY+Cv\n5iU/i1kjx3dZC+FPVv2xglV/rKBmwVoMbzhG7Tgit3E6CVq+GOuUSWivXMYXHk7asNGkd+4GFova\n6YSQQhaB4eDVAwze+g5hpnzMa7YYky5QzocVD8zjwfTxKqyTxqM7ewafNRjbgMGk9+yDEhqmdjoh\nMkghC7+X5k6j68Y3SPekM6fJAkqGllI7ksgNfD6MX3yGdcIY9EePoJhM2Hv0wd7vHZQCBdROJ8T/\nkEIWfk1RFKK/f5sjNw7zZo3etCrzrNqRhNoUBeN3X2MZNxrD/r0oOh3p7TthHxCNr4gsIiJyLylk\n4ddWHFzK6sMfUrtQHeLrj1Q7jlCZ4eefsI4bheGXn1E0GhwvtsU2KAZfmbJqRxPirqSQhd/6Pfk3\nYn8YRL4/jxsbdYF/hqy4Pf3e3VjHjcK4+VsAnC2ewTYkDm+VqionE+LeSSELv5TmSqXrpjdweB28\n33wJxUNkxZ28SHfoD6wJYzF98RkArscbYYuNx1Nb5i0X/kcKWfgdRVEYsKUfx24cpXfUWzQr1VLt\nSCKHaU+dxJo4AdPHq9D4fLhr18EWMwz3E43UjibEfZNCFn5nye8L+fToJ9QtXI/YesPUjiNy0oUL\nBA8dRtDyJWjcbjyVq2KLHYarWQuZ5lL4PSlk4Vf2X9lL/E9DiAiKYH6zxRh0BrUjiRyguXYVy8xp\nsGAu5vR0PKXLYB88FOcLL4L2rqvICuEXpJCF30hx3qTLxjdwep0sbrGCIsHyFZZAp0lLxTx3NubZ\nM9CmpkDRoqS+MxjHK6+DQf4xJgKLFLLwC4qi8PaWvpxMOcFbtQbwdMlmakcS2Sk9HfPiBVimT0Z7\n9Sq+/PlJGzWO4EFv40h1q51OiGwhhSz8wsLf5vH5sbU0KPIogx8ZqnYckV3cboI+WI5lcgK6C+fx\nhYRiGxJHeveeKMEhBAcFgRSyCFBSyCLX23M5iWE/xVLAXIC5TRei18qPbcDx+TB9uhprwlh0J0+g\nmM3Y+76Nvc9bKOERaqcTIkfIbzaRq9103qDrpo54fB5mN3mfwtaH1I4kspKiYNy4Huv40egP/o5i\nMJDeuRv2twfhK1RY7XRC5CgpZJFrKYpCv+96cTrlJO/UiaZR8cZqRxJZyLB1C9ZxIzEk7ULRanG8\n8jq2gUPwlSipdjQhVCGFLHKtuftmsf7EFzxW9AkG1YlRO47IIvqdO7COH43xh+8BcD73ArbBQ/FW\nqKhyMiHUJYUscqWdF3cw6udhRJoLMqfpAnRandqRxAPS/f4b1oQxmDZ8BYCrcRNsMfF4atRUOZkQ\nuYMUssh1rjuu0X1TJ3yKj/eaLqCQpZDakcQD0B4/hnXiOEyfrkajKLjrNcAWOwx3g0fVjiZEriKF\nLHIVn+Kj77c9OJt2hui6sTxe7Em1I4n7pD13FsuUiQStXIbG68VdrQb22HhcjZvKNJdC3IYUsshV\nZu+ZwaZTG3ii2FO8XXuQ2nHEfdAkJ2OZNhnz4vfROJ14ypXHFhOP65nnZZpLIe5AClnkGr9c2M7Y\n7SMoZCnMnCbvy3FjP6NJuYl59gzMc2ejtaXhLV4C26AYnG1eBr38qhHibuRvicgVrqZfpfumjigo\nzG26kEhLpNqRxL2y2zG/PxfLzHfR3riBL7IgqXHDcbTrCCaT2umE8BtSyEJ1PsVH72+7ccF2nth6\nw2hY9DG1I4l74XIRtGwxlncnobt8CV9YPtLiRpDe5U2wWtVOJ4TfkUIWqpuR9C7fnf6GxiWa0K/W\nO2rHEXfj9WL6eBXWxAnoTp9CsVixvTOI9J59UcLyqZ1OCL8lhSxU9fP5nxi/YzQPWYsw6+n5aDVy\n0k+upSgYv1iHNWEM+sOHUIxG7G/2wt5vAEqkHGIQ4kFJIQvVXLFfofumTmjQMK/ZYvKb86sdSdyO\nomDY/A3W8WMw7N2NotOR3q4D9nei8RUrrnY6IQKGFLJQhdfnpdc3Xblkv0h8g1HUe6i+2pHEbRi2\nb8MybhTG7dsAcPz7ReyDh+ItU07lZEIEHilkoYqpSYl8f3YzTUs2p3dUP7XjiL/R79uDZfxoTN9+\nDYCzeUtsg+PwPlxN5WRCBC4pZJHjfjy3lUm/jqdocDFmPP2eHDfORXRHDmNJGEvQuk8BcD36OLbY\nYXjq1lM5mRCBTwpZ5KhL9ku8uakzWo2W+c0WExEkx41zA+3pU1gTJ2D66AM0Ph/umrWwxQ7H/UQj\nmeZSiBwihSxyjNfnpefXXbiSfpmRDcdRp/AjakfK8zSXLmGdOomgpYvQuN14KlXGNiQeV8tnpIiF\nyGFSyCLHJO6cwI/nttKi9DP0qNFb7Th5mub6NSyzpmOePwdNejrekqWwDR6K899tQCdTlgqhBilk\nkSO2nPmOKTsnUiKkJNOfmo1GPn2pIy0Ny/w5mGdNR5tyE2/hh7CPGo/jtfZgMKidTog8TQpZZLuL\ntgv0+qYreq2e+c0Wky8oXO1IeY/DgXnpQixTE9EmJ+OLiCBtxFjSO3UFs1ntdEIIpJBFNvP4PLz5\ndWeS05MZ+1gCNQvVVjtS3uLxELRqBZbECejOn8MXHIJtUAzpPXqjhISqnU4I8V+kkEW2mrhjHD+f\n/4lny/yLrtV6qB0n7/D5MH22BkvCWPTHj6EEBWHv/Rb2vv1RIuTMdiFyIylkkW2+O/01U5MSKRla\niqlPzZTjxjlBUTB+vQHruNHoD/yGoteT3rHLrWkuCz+kdjohxB1IIYtscT7tHL2+6YZRa2RB86WE\nmsLUjhTwDD9uxTp2JIZdv6JoNDheegXboBh8pUqrHU0IcQ+kkEWWc3vddN/UiWuOa0x4YjLVI6PU\njhTQ9Ek7sY4bjXHrZgCczzyPbfBQvJUqq5xMCJEZUsgiy43fMZodF7fzQrnWdKraVe04AUt38ADW\nCWMwrf8CAFejxthi4vHUlBPnhPBHUsgiS206uZ6Zu6dSJqwskxtNl+PG2UB74jjWSeMxffIRGkXB\nXbcetthhuB99XO1oQogHIIUssszZ1DP0/bYHJp2J+c2XEGKUr9VkJe2F81gmTyRo5VI0Hg+eqtWw\nxcbjatJcprkUIgBIIYss4fK66LapI9ed10l8chrVClRXO1LA0Fy9imX6FMyL5qNxOPCULYd9SBzO\n514ArayUJUSgkEIWWWLM9hHsuvQrrcu/RPsqHdWOExA0qSmY58zEPGcmWlsa3qLFsA+KwdH2VdDL\nX10hAo38rRYPbP2JL3lv70zK5StPYqNpctz4QdntmBfOxzLzXbTXruErEElabDzpb3QGk0ntdEKI\nbCKFLB7IqZST9PuuJ2a9mfebLyXYEKx2JP/lchG0YimWKRPRXbqILzQMW0w89m49IVjGVYhAJ4Us\n7pvL66L7po7cdN5g6lOzqJK/qtqR/JPXi+mTj7BOHI/u9EkUiwVb/4Gk9+qLkk8W4hAir5BCVlly\nejIGrZ4QYyhajX+doDNyWxy7LyfRtuKrvFqpndpx/I+iYPzqC6wTRqM/9AeK0Yi9Ww/sbw1EKVhQ\n7XRCiBwmhaySo9ePMOynGL45vQkADRqCjSGEGkMJNYYRagolzBhGiDH0z8v5CDGFEmq8dXuoKZQQ\n463b/3PZorfk2PHbz499xvz971ExvBIJT0yR48aZoSgYtnyHdfwoDHt2o2i1pL/WHvuAwfiKl1A7\nnRBCJVLIOeym8waTd07k/f3v4fF5qF2oLgXMBUhxpZDiTCHFdZPztnP8ce0ACkqmtq3X6gk1/lnU\npnz/dTnsL0Ufagz7r8uhhJr+vG4Mxagz3vV1Ttw8Tv/NvbHoLbzffClWg/V+hyPP0f+yHev4URi3\n/QiA41+tsQ8eirdceZWTCSHUJoWcQ7w+Lyv/WMb4X0aRnJ5MidBSjGw4llaln73tp0uf4sPmTiPF\nmcJN101SXCmkOm/+1+U/b3emkOK68ZdCT3GlcPT6EeweW6ZzmvXmW5/K/yzy/MERBGElzBSWcfvn\nxz4j1ZXCjMbvUTGiUlYMT+Dbs4fQ6CGYvt4IgLNpc+xD4vBUq6FyMCFEbiGFnAN+Pv8TQ38czG/J\n+7DorQytN5w3a/QmSB/0j8/RarSE/PkJtyjF7ut13V43qe4UbjpvkupKIcX1X5dvV+5/3p7iuskN\n53VOpZzEfcl9222/Vqk9L1d67b5y5SW6o0ewTBwLa9dgAlwNHsUWOxxPvfpqRxNC5DJSyNnoTOpp\nRm0bxmfH1gDQtuKrxNUfQWFrzqxLa9AZiNDlJyLo/hakVxSFkHADx86fyyjqm86baDVaHi/6ZBan\nDSzas2ewJE4gaNUKND4f1K7Njeg43I0ayzSXQojbkkLOBja3jZm7pzJr9zQcXge1CtZm7OMTqV2o\nrtrRMkWj0WA2mClkKUQhSyG14/gFzeXLWKYlYl6yEI3LhadiJWyD4wjr+Bru5DS14wkhcjEp5Cyk\nKAqfHl3NqG3DOG87RyFLYRIbjKRNhZf97itNInM0N65jnj0Dy7zZaOx2vCVKYYuOwfliW9Dp5FOx\nEOKu7qklHA4HTZo0Yc2aW7tely5dStWqVbHZ/v+koXXr1vHiiy/y0ksv8fHHH2dP2lxs7+XdPPdp\nc3p83YWrjmT61xrIz6/f+o6ulHEAs9kwT5tMRN0aWKcm4gsJJTVhCte27cTZ9tVbZSyEEPfgnj4h\nz5kzh7CwMADWrl3L1atXKfhfExfY7XZmzZrF6tWrMRgMtGnThqZNm5IvX77sSZ2LXLJfYvz2UXzw\nx3IUFJ4p8zzDG4ymVFhptaOJ7OR0ErRsEdYpk9AmX8EXHk7asNGkd+4GFova6YQQfuiuhXzs2DGO\nHj1Ko0aNAGjSpAnBwcF8/vnnGY/Zu3cv1apVIyQkBIBatWqRlJRE48aNsyd1LuD0Opm/7z2m7JxI\nmjuVyhFVGfPYBB4vJic7BTSPh6CPPsCSOAHd2TP4rMHYBg4hvUdvlNAwtdMJIfzYXQs5ISGB+Ph4\n1q5dC0DwbSa5T05OJiIiIuN6REQEV65cycKYuYeiKGw6tYFhP8Vw4uZxIoIiSGgwhfZVOqLXyiH5\ngOXzYfp8LZYJY9AfO4piMmHv2Rd737dRChRQO50QIgDcsUHWrl1LVFQUxYsXz9RGFeXeZpgKD7eg\n12fvMbbIyJAs29aBKwd4e9PbbDq2CZ1GR79H+jG80XAizBF3f7Ify8ox9DuKAuvXw9ChsGfPrXWI\n33wTTVwclmLFyMzO6Tw9jllIxvHByRhmjawexzsW8pYtWzhz5gxbtmzh4sWLGI1GChcuTMOGDf/y\nuIIFC5KcnJxx/fLly0RFRd31xa9ft99n7HsTGRnClSupD7ydG47rJO6cwIL98/AqXp4s9hRjHkug\nYkQlvGlwJe3BXyO3yqox9EeGbT9iHTsSw6+/oGg0ONu8jG1QDL7SZW49IBPjkpfHMSvJOD44GcOs\ncb/jeKcSv2MhT506NePyjBkzKFq06P+UMUCNGjWIi4sjJSUFnU5HUlISsbGxmQ6a23h8HpYdWEzC\njjFcc1yjdFgZRj06nmYlW8hiCgFMvycJ67hRGLd8B4Cz5bPYhsThrVxF3WBCiICW6YOec+bMYdu2\nbVy5coVu3boRFRVFdHQ0AwYMoEuXLmg0Gnr37p1xgpe/+vHcVob+MJiD134n2BDCsAaj6Va9Byad\nSe1oIpvoDv2BdcIYTF+uA8D1xFPYYuPx1KqjcjIhRF6gUe71gG82yO7dJvezS+FUyklGbIvjy+Pr\n0KDh1UrtiKk/LM/OVJUXdm9pT53EOmk8po9XoVEU3LXrYosdhvvxrDtjPi+MY06QcXxwMoZZI8d3\nWeclae40ZiRNYfaeGTi9TuoWrsfYxxKIKlhL7Wgim2gvXsAyZSJBK5aicbvxVHkYW2w8rqYtZGYt\nIUSOy/OF7FN8fHL4I0ZvH85F2wWKWIsyrOEo/l2ujRwnDlCaa1exzJiKecFcNA4HntJlsA+Jw/mv\n1qCVWdWEEOrI04WcdGknQ38czK5LvxKkC2JgnSH0rvkWVoNV7WgiG2jSUjG/Nwvz7Blo01LxFimK\nfeAQHC+/BgaD2vGEEHlcnizki7YLjNk+go8OfQDAv8q2ZljDURQPKaFyMpEt0tMxL16AZfpktFev\n4itQgLTBsaR36AJB/7wmtRBC5KQ8VcgOj4O5e2fx7q5E7B4bDxeoztjHEmhQ5FG1o4ns4HYTtHIZ\nlskJ6C5ewBcahi0mHnu3nnCbGeeEEEJNeaKQFUVh/YkvGb4tllMpJylgLsDox8bzWqX26LSyGk/A\n8Xoxfboa68Rx6E6eQDGbsfd7B3vvfijhgT2rmhDCfwV8IR+8eoC4n4bww9kt6LV6etTow4A60YSZ\nAn8lqjxHUTBu+ArrhNHoDx5AMRhI79IdW/9BKIXy5tfWhBD+I2AL+ZrjKiO/imHOzjn4FB9NSzZn\nZMNxlAsvr3Y0kQ0MW7dgHTcSQ9IuFK2W9FfbYR8wGF+JkmpHE0KIexJwhezxeVjy+wISdozlhvMG\n5fKVZ/Sj43m6ZDO1o4lsoN+5A+v40Rh/+B4Ax/P/xj54KN7yFVROJoQQmRNQhfz9mc3E/zSEP64d\nJNQYxrvN36VtqTcw6OQrLYFG9/tvWCeMxrRxPQDOp5tij4nHU/3ui5oIIURuFDCFvO7op3Td1AEN\nGtpX6URMvXgqlygtU8QFGN3xo1gmjsP06Se3prms1wDb0OG46//voidCCOFPAqaQK0RUol3lDnSq\n1o1qBaqrHUdkMe25s7emuVy5DI3Xi7taDWxDh+F+qolMcymECAgBU8iVIioz5akZascQWUyTnIxl\n2mTMi99H43TiKV8B25A4XM88L9NcCiECSsAUsggsmps3MM+ZgXnuHLS2NLzFS2AbFIOzzcuglx9b\nIUTgkd9sInex2zG/PxfLzHfR3riBL7IgqXEjcLTrACZZi1oIEbikkEXu4HIRtGwxlncnobt8CV++\nfKTFjSS9S3ewymIfQojAJ4Us1OX1Yvp4FdbECehOn0KxWLG9M4j0nn1RwmQ2NSFE3iGFLNTh82H8\nch3WhLHoDx9CMZmwv9kbe793UCIj1U4nhBA5TgpZ5CxFwbD5G6zjRmPYtwdFpyO9fUfs70TjK1pM\n7XRCCKEaKWSRYwzbt2EZNwrj9m0AOFq3wR4di7dMOZWTCSGE+qSQRbbT79uDZfxoTN9+DYCzeUts\ng+PwPlxN5WRCCJF7SCGLbKM7chhLwliC1n0KgOvRx7HFDsNTt57KyYQQIveRQhZZTnv6FNbECZg+\n+gCNz4e7Vm1sMcNwP9FIprkUQoh/IIUssozm0iWsUycRtHQRGrcbT6XK2GKG4WrRSopYCCHuQgpZ\nPDDN9WtYZk3HPH8OmvR0vCVLYRs8FOe/24BOp3Y8IYTwC1LI4v6lpWGZPwfzrOloU27iLfwQ9lHj\ncbzWHgyyBrUQQmSGFLLIPIcD89KFWKYmok1OxhcRQdqIsaR36gpms9rphBDCL0khi3vn8RC0agWW\nyQnozp3FFxyCLTqW9Dd7oYSEqp1OCCH8mhSyuDufD9Nna7AkjEV//BhKUBD23m9h79sfJSK/2umE\nECIgSCGLf6Yo8MUXhA+OQX/gNxS9nvSOXW5Nc1n4IbXTCSFEQJFCFrdl+HEr1rEjYdev6DQaHC+9\ngm1QDL5SpdWOJoQQAUkKWfyFPmkn1nGjMW7dfOuG1q253n8w3kqV1Q0mhBABTgpZAKA7eADrhDGY\n1n8BgKtRY2wx8YQ3a4T3SqrK6YQQIvBJIedx2hPHsU4aj+mTj9AoCu669bDFDsP96ONqRxNCiDxF\nCjmP0l44j2XyRIJWLkXj8eCpWg3b0GG4nm4m01wKIYQKpJDzGM3Vq1imT8G8aD4ahwPP/7V3/0FR\nHvgZwJ/dhYV9FwQxEKPRdnrnmZwRrcae1CERMBYjGi8QQEqsVdEY4lXU8MOES9AYEA0mmvij9gye\n3jXecD2H9rwxTiltHA35oZdTE0EjCcYcAQqK7rvsyrvf/uG5TXIqa1x4X5bnM+MMyrvw8Azy8O4u\nL9/7PtTC5+GaNQcwm/WOR0Q0YHGQBwjT5U7Ytr0O27bXYXZcgTb8XqjPFqErfS4QxE8DIiK98Stx\noFNV2HbthLKlAuaODngeIzIAAAy5SURBVHjuisaV1cVwzlsAhITonY6IiP6Egxyo3G6E/uLnUCrK\nYfmqGZ6ISFx57gU4Fy4BwsL0TkdERN/CQQ40moaQX/8K9vJSWJo+gygKHMtXwfn0MkjkYL3TERHR\nTXCQA4UIrAf+A/aytQiqPw2xWqHmPAX1n1ZBYmL0TkdERD3gIPd3IgiurYG9dA2Cf38cYjbDmfUk\n1JUF8IwYqXc6IiLyEQe5Hwuqexf20jWwHjkMAOia8zjU/OegfX+UzsmIiOh2cZD7IcuJP8BethYh\nhw4CAFyP/B0chcXQxsbqnIyIiL4rDnI/Yjl7Bkr5OoTu/zcAgDtuChyrX0D3jybrnIyIiO4UB7kf\nMH9xHsrGMoS+9QuYPB5cHffX1643PTWRl7kkIgoQHGQDM7W0QHltI2y7d8HkdqN79H1wFDwP98xZ\nHGIiogDDQTYg08UO2LZugfLPW2FSVWgj/xKO/CK4UtMBi0XveERE1As4yEbicMD2L9uhvP4azJcu\nQrt7KNQXXkLX388DrFa90xERUS/iIBuBywXbz3dB2bQR5rZWeAYPxpWfroVzQQ6gKHqnIyKiPsBB\n1lN3N0J/9a9QNpbB8sV5eOxhcKwqhPOpXMigCL3TERFRH+Ig68HjQci/74dS9hKCPj0LCQmBunQZ\n1GV5kLvu0jsdERHpgIPcl0Rg/c+3oby8FsEn/wAJCoLzyX+EujIfnmHD9U5HREQ64iD3keAjh2Ff\nV4Lg9+sgJhO6UtPheLYInr/6nt7RiIjIADjIvSzo98dgf3kNrLU1AADXjBQ4Cp+Hdv8P9Q1GRESG\nwkHuJZb607CXvYSQ31YDANwPJcBR9Dy6J07SORkRERmRT4Pc1dWFlJQUPP3004iLi0N+fj40TUN0\ndDQ2bNgAq9WKMWPGYMKECd7bVFZWwjIAL2Jh/qwR9g2lCKnaB5MIrk6cdO0yl/EP6x2NiIgMzKdB\n3rZtGyIirv0YzubNm5GVlYUZM2agoqICVVVVyMrKQlhYGPbs2dOrYY3M3PxHKBXlCN27G6bubnT/\n8AE4VhfD/UgyL3NJREQ9Mvd0wKeffoqzZ89i6tSpAIC6ujokJSUBABISEnD06NFeDWh0pvb/hb2k\nGFF/Mw62yp9BGzESnTt2oaPmMNzTZ3CMiYjIJz0O8vr161FYWOj9u9PphPVPl3EcMmQIWltbAQBu\ntxsrV65EZmYm3nzzzV6KaxymK5ehbCxD1IOxUN54DZ6oIbhcsQUdh9+H68dpgLnHaomIiLxueZf1\n/v37MX78eIwYMeKGrxcR78v5+fmYPXs2TCYTsrOz8eCDD2Ls2LG3fOeDBysICurdx5mjo8P9+wad\nTmDrVqCsDGhrA6KjgbVrYHnqKYSHhsLP780Q/N7hAMUe/YM93jl26B/+7vGWg1xbW4vz58+jtrYW\nzc3NsFqtUBQFXV1dCA0NxVdffYWYmBgAwNy5c723mzx5MhoaGnoc5I4O1Q8fws1FR4ejtfWyf97Y\n1asI/eUeKK+sh6X5j/AMioCzqBhqzlIgLAy4fPXanwDj1w4HMPboH+zxzrFD//iuPd5qxG85yK++\n+qr35S1btmD48OE4fvw4Dh48iMceewxvv/024uPjce7cObzxxhvYuHEjNE3DsWPHkJycfNtBDUnT\nEPKbKtjLX4bls0aIzQb1Jyug5v4EMjhK73RERBQgbvvnkJctW4aCggLs27cPw4YNw5w5cxAcHIyh\nQ4ciLS0NZrMZiYmJiI2N7Y28fUcE1t/9Fvb1LyHok48hwcFwLlwMdfkqeO4eqnc6IiIKMCb5+gPB\nfay37zb5rncpBP/3f8FeugbBxz6EmM1wpc+FY1UhPCP/ohdSGhvv3vIP9ugf7PHOsUP/6PO7rAea\noPfrYC9dC+vh/wEAdM3+MdT81dB+MFrnZEREFOg4yAAsp07CXrYWIQd/BwBwJT0CtagY3bHjdU5G\nREQDxYAeZMu5s1DKX0bIb3597TKXP4qD47kXcHXy3+odjYiIBpgBOcjmC19cu8zlL/fApGm4Gjse\njtXFuJowjVfWIiIiXQyoQTa1tkLZ/ApslT+DyeVC96gfwFFYDHfKbA4xERHpakAMsunSRdi2bYGy\nfStMqgPaiJFwPFsE1xOZwAD8jVRERGQ8gT3IDgdsmzdBeX0TzBcvQou5G2pxCbqy/wEICdE7HRER\nkVdgDrLLhdC9lcBrryCsuRmeyEhcKV4D58LFgKLonY6IiOjPBNYgd3cjpGof7BtKYTnfBNjtcKzI\nh3PpM5CISL3TERER3VTADLLlTAMGzc9C0JkGSEgI1CW5UNb8FKrJpnc0IiKiHgXMIAedOgFL4zk4\nn5wPdWUBPMOGQ4kOB3iJOCIi6gcCZpBdc1LhSnkMCAqYD4mIiAYQs94B/IpjTERE/VRgDTIREVE/\nxUEmIiIyAA4yERGRAXCQiYiIDICDTEREZAAcZCIiIgPgIBMRERkAB5mIiMgAOMhEREQGwEEmIiIy\nAA4yERGRAZhERPQOQURENNDxDJmIiMgAOMhEREQGwEEmIiIyAA4yERGRAXCQiYiIDICDTEREZABB\nege4U+Xl5fjwww/R3d2NJUuWYPr06QCAd955B4sWLUJ9fT0A4PTp01i9ejUAICkpCbm5ubplNiJf\ne9y0aRPq6uogIpg2bRpycnL0jG0o3+6wpqYGp06dQmRkJABg4cKFmDp1Kqqrq7F7926YzWakp6fj\niSee0Dm5sfja44EDB7Br1y6YzWbExcUhLy9P5+TG4muP161YsQJWqxVlZWU6JTYeXzv0275IP3b0\n6FFZtGiRiIi0t7fLww8/LCIiXV1dkp2dLVOmTPEem5aWJidPnhRN0yQvL09UVdUjsiH52mN9fb1k\nZGSIiIimaZKcnCwtLS26ZDaaG3VYUFAgNTU13zjO4XDI9OnTpbOzU5xOp8ycOVM6Ojr0iGxIvvao\nqqokJCTI5cuXxePxSFpampw5c0aPyIbka4/XHT58WFJTU6WgoKAvYxra7XTor33p12fIkyZNQmxs\nLABg0KBBcDqd0DQN27dvR1ZWFjZs2AAAaGtrg6qqGDNmDACgoqJCt8xG5GuP4eHhcLlccLvd0DQN\nZrMZNptNz+iGcbMOv+2jjz7C2LFjER4eDgCYMGECjh07hsTExD7Na1S+9miz2VBdXY2wsDAAQGRk\nJC5evNinWY3M1x4BwO12Y9u2bVi6dCkOHTrUlzENzdcO/bkv/foxZIvFAkVRAABVVVV46KGH0NTU\nhNOnT2PGjBne4y5cuICIiAgUFhYiMzMTlZWVOiU2Jl97vOeee5CcnIyEhAQkJCQgMzPT+wVxoLtR\nhxaLBXv37sW8efOQl5eH9vZ2tLW1ISoqynu7qKgotLa26hXbcHztEYD3c6++vh4XLlzAuHHjdMtt\nNLfT444dOzB37lz+X/4WXzv0677c0Tm9QRw6dEjS0tKks7NTcnJy5PPPPxcRkYSEBBEROX78uMTH\nx0t7e7uoqiqzZs2ShoYGPSMbUk89NjU1SWpqqqiqKp2dnfLoo49KW1ubnpEN5+sdHjlyRD7++GMR\nEdmxY4eUlJRIdXW1rFu3znt8RUWFvPXWW3rFNayeeryusbFRUlJSvK+nb+qpx8bGRlm8eLGIiLz7\n7ru8y/oGeurQn/vSr8+QgWtPOtq+fTt27twJVVVx7tw5rFq1Cunp6WhpaUF2djaGDBmCUaNGYfDg\nwbDZbJg4cSLOnDmjd3RD8aXHEydOYNy4cbDZbAgPD8fo0aPR0NCgd3TD+HqH4eHhiIuLw/333w8A\nSExMRENDA2JiYtDW1ua9TUtLC2JiYvSKbEi+9AgAzc3NyM3NRVlZmff19P986bG2thZffvkl0tPT\nUVJSgtraWuzcuVPn5MbhS4d+3Rd/fifR1zo7OyUlJeWmZ2nXz+xERDIyMqSjo0M0TZOMjAz55JNP\n+iqm4fna44kTJyQ9PV00TRO32y0zZ86U8+fP92VUw7pRh88884w0NTWJiMjevXvlxRdfFKfTKdOm\nTZNLly7JlStXvE/womt87VFEZMGCBfLee+/pktPobqfH63iG/E2306G/9qVfP6nrwIED6OjowPLl\ny73/tn79egwbNuzPji0qKkJOTg5MJhPi4+Nx33339WVUQ/O1xwceeABTpkxBVlYWACAtLQ333ntv\nn2Y1qht1+Pjjj2P58uWw2WxQFAWlpaUIDQ3FypUrsXDhQphMJuTm5nqf4EW+99jY2IgPPvgAmzdv\n9h43f/58JCUl6RHbcHztkW7udjr0177w1y8SEREZQL9/DJmIiCgQcJCJiIgMgINMRERkABxkIiIi\nA+AgExERGQAHmYiIyAA4yERERAbAQSYiIjKA/wNbFvt2OzXA3QAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
},
{
"metadata": {
@@ -550,8 +790,24 @@
"cell_type": "code",
"source": [
"def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n",
+ " \n",
+ "\n",
" # YOUR CODE HERE\n",
- " pass"
+ " with tf.Session() as sess:\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " pred_train, current_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ "\n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', current_loss)\n",
+ "\n",
+ " print ('Now testing the model in the test set')\n",
+ " final_pred, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " return\n"
],
"execution_count": 0,
"outputs": []
@@ -560,15 +816,38 @@
"metadata": {
"id": "A6MaclhK4rc6",
"colab_type": "code",
- "colab": {}
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 221
+ },
+ "outputId": "9988175d-c6f6-4cea-81a1-dc213bf5710c"
},
"cell_type": "code",
"source": [
"# Okay! Now let's tweak!\n",
"linear_regression(learning_rate=0.000034, n_epochs=500)"
],
- "execution_count": 0,
- "outputs": []
+ "execution_count": 28,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 48241.758\n",
+ "Loss after epoch 50 is 29.843296\n",
+ "Loss after epoch 100 is 29.832943\n",
+ "Loss after epoch 150 is 29.822683\n",
+ "Loss after epoch 200 is 29.812458\n",
+ "Loss after epoch 250 is 29.802202\n",
+ "Loss after epoch 300 is 29.791937\n",
+ "Loss after epoch 350 is 29.781736\n",
+ "Loss after epoch 400 is 29.771505\n",
+ "Loss after epoch 450 is 29.761292\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 35.814262\n"
+ ],
+ "name": "stdout"
+ }
+ ]
},
{
"metadata": {
@@ -601,7 +880,278 @@
},
"cell_type": "code",
"source": [
- "# YOUR CODE HERE"
+ "# YOUR CODE HERE\n",
+ "def linear_regression(learning_rate=0.0000001, n_epochs=1000, interval=100):\n",
+ " # YOUR CODE HERE\n",
+ " with tf.Session() as sess:\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " pred_train, current_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ "\n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', current_loss)\n",
+ "\n",
+ " print ('Now testing the model in the test set')\n",
+ " final_pred, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " return\n"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "0knOp0SUmOoy",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 136
+ },
+ "outputId": "087d8c9e-c3e5-4d8d-93a6-14c57d3ac642"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.8, n_epochs=200000, interval=40000)"
+ ],
+ "execution_count": 44,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 48241.758\n",
+ "Loss after epoch 40000 is 22.710217\n",
+ "Loss after epoch 80000 is 17.332392\n",
+ "Loss after epoch 120000 is 13.283219\n",
+ "Loss after epoch 160000 is 10.234737\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 9.740068\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4smcXWZdnYy1",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 221
+ },
+ "outputId": "ce2609e8-e1b0-4c10-ea16-84cdadceeb9f"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.08, n_epochs=300000, interval=30000)"
+ ],
+ "execution_count": 45,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 48241.758\n",
+ "Loss after epoch 30000 is 24.310637\n",
+ "Loss after epoch 60000 is 19.8307\n",
+ "Loss after epoch 90000 is 16.209751\n",
+ "Loss after epoch 120000 is 13.283219\n",
+ "Loss after epoch 150000 is 10.9177685\n",
+ "Loss after epoch 180000 is 9.004981\n",
+ "Loss after epoch 210000 is 7.460944\n",
+ "Loss after epoch 240000 is 6.211317\n",
+ "Loss after epoch 270000 is 5.2022204\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 5.4466424\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "49PIqfuWqIBm",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 221
+ },
+ "outputId": "b54c1e77-b080-4f67-87af-9dc0c3e511c6"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.8, n_epochs=500000, interval=50000)"
+ ],
+ "execution_count": 46,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 48241.758\n",
+ "Loss after epoch 50000 is 21.219416\n",
+ "Loss after epoch 100000 is 15.16438\n",
+ "Loss after epoch 150000 is 10.9177685\n",
+ "Loss after epoch 200000 is 7.9400454\n",
+ "Loss after epoch 250000 is 5.8506804\n",
+ "Loss after epoch 300000 is 4.386475\n",
+ "Loss after epoch 350000 is 3.3583517\n",
+ "Loss after epoch 400000 is 2.6385438\n",
+ "Loss after epoch 450000 is 2.132647\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 2.2477086\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "I0IaSFJ1q2LT",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 221
+ },
+ "outputId": "d5666f1e-b748-4f41-9a66-b68ef24da17e"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.08, n_epochs=500000, interval=50000)"
+ ],
+ "execution_count": 47,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 48241.758\n",
+ "Loss after epoch 50000 is 21.219416\n",
+ "Loss after epoch 100000 is 15.16438\n",
+ "Loss after epoch 150000 is 10.9177685\n",
+ "Loss after epoch 200000 is 7.9400454\n",
+ "Loss after epoch 250000 is 5.8506804\n",
+ "Loss after epoch 300000 is 4.386475\n",
+ "Loss after epoch 350000 is 3.3583517\n",
+ "Loss after epoch 400000 is 2.6385438\n",
+ "Loss after epoch 450000 is 2.132647\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 2.2477086\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4b7eBOolq412",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 391
+ },
+ "outputId": "b7245316-aa82-4f24-e7be-085bc9b6e95e"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.8, n_epochs=1000000, interval=50000)"
+ ],
+ "execution_count": 48,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 48241.758\n",
+ "Loss after epoch 50000 is 21.219416\n",
+ "Loss after epoch 100000 is 15.16438\n",
+ "Loss after epoch 150000 is 10.9177685\n",
+ "Loss after epoch 200000 is 7.9400454\n",
+ "Loss after epoch 250000 is 5.8506804\n",
+ "Loss after epoch 300000 is 4.386475\n",
+ "Loss after epoch 350000 is 3.3583517\n",
+ "Loss after epoch 400000 is 2.6385438\n",
+ "Loss after epoch 450000 is 2.132647\n",
+ "Loss after epoch 500000 is 1.7783551\n",
+ "Loss after epoch 550000 is 1.5294437\n",
+ "Loss after epoch 600000 is 1.3565342\n",
+ "Loss after epoch 650000 is 1.2327821\n",
+ "Loss after epoch 700000 is 1.1488175\n",
+ "Loss after epoch 750000 is 1.088131\n",
+ "Loss after epoch 800000 is 1.0485603\n",
+ "Loss after epoch 850000 is 1.0154438\n",
+ "Loss after epoch 900000 is 0.99606717\n",
+ "Loss after epoch 950000 is 0.9841915\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 1.2012733\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "cI9eNZeHsnz8",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 561
+ },
+ "outputId": "67fa45be-856c-49fa-8835-9d629e99ba7c"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.8, n_epochs=3000000, interval=100000)"
+ ],
+ "execution_count": 49,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 48241.758\n",
+ "Loss after epoch 100000 is 15.16438\n",
+ "Loss after epoch 200000 is 7.9400454\n",
+ "Loss after epoch 300000 is 4.386475\n",
+ "Loss after epoch 400000 is 2.6385438\n",
+ "Loss after epoch 500000 is 1.7783551\n",
+ "Loss after epoch 600000 is 1.3565342\n",
+ "Loss after epoch 700000 is 1.1488175\n",
+ "Loss after epoch 800000 is 1.0485603\n",
+ "Loss after epoch 900000 is 0.99606717\n",
+ "Loss after epoch 1000000 is 0.9739313\n",
+ "Loss after epoch 1100000 is 0.9582495\n",
+ "Loss after epoch 1200000 is 0.9526469\n",
+ "Loss after epoch 1300000 is 0.9526469\n",
+ "Loss after epoch 1400000 is 0.9526469\n",
+ "Loss after epoch 1500000 is 0.9526469\n",
+ "Loss after epoch 1600000 is 0.9526469\n",
+ "Loss after epoch 1700000 is 0.9526469\n",
+ "Loss after epoch 1800000 is 0.9526469\n",
+ "Loss after epoch 1900000 is 0.9526469\n",
+ "Loss after epoch 2000000 is 0.9526469\n",
+ "Loss after epoch 2100000 is 0.9526469\n",
+ "Loss after epoch 2200000 is 0.9526469\n",
+ "Loss after epoch 2300000 is 0.9526469\n",
+ "Loss after epoch 2400000 is 0.9526469\n",
+ "Loss after epoch 2500000 is 0.9526469\n",
+ "Loss after epoch 2600000 is 0.9526469\n",
+ "Loss after epoch 2700000 is 0.9526469\n",
+ "Loss after epoch 2800000 is 0.9526469\n",
+ "Loss after epoch 2900000 is 0.9526469\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 1.1648217\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "mjeM--rNujcm",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ ""
],
"execution_count": 0,
"outputs": []
diff --git a/First_Date_with_TensorFlow.ipynb b/First_Date_with_TensorFlow.ipynb
deleted file mode 100644
index a5b7fc0..0000000
--- a/First_Date_with_TensorFlow.ipynb
+++ /dev/null
@@ -1,1030 +0,0 @@
-{
- "nbformat": 4,
- "nbformat_minor": 0,
- "metadata": {
- "colab": {
- "name": "First_Date_with_TensorFlow.ipynb",
- "version": "0.3.2",
- "provenance": [],
- "include_colab_link": true
- },
- "kernelspec": {
- "name": "python3",
- "display_name": "Python 3"
- }
- },
- "cells": [
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "view-in-github",
- "colab_type": "text"
- },
- "source": [
- "[View in Colaboratory](https://colab.research.google.com/github/abhiWriteCode/Assignment-4/blob/AGCreates/First_Date_with_TensorFlow.ipynb)"
- ]
- },
- {
- "metadata": {
- "id": "2XXfXed5YLbe",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "# First Date with TensorFlow\n",
- "\n",
- "Hi all,
\n",
- "\n",
- "You know what's important for understanding Deep Learning / Machine Learning?
\n",
- "Intuition. Period.\n",
- "\n",
- "And Intuition comes when you run the code multiple times.\n",
- "\n",
- "So, today I can write a couple of defination and say this is this, this is that.
\n",
- "You Google half of the things up. You find answers which you need to Google further.
\n",
- "In the process, you probably won't even remember what's the first thing you started out with!\n",
- "\n",
- "So?\n",
- "\n",
- "Hence on, I will execute cells with code.
\n",
- "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
- "**No Theory Just Code.**\n",
- "\n",
- "I will at max give a defination that extends for a line. That's it.
\n",
- "Let's get started!\n",
- "\n",
- "
\n",
- "\n",
- "**RECOMMENDED!**
\n",
- "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
- "Don't just `shift+enter` the cells.\n",
- "\n",
- "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
- ]
- },
- {
- "metadata": {
- "id": "gYWUpE-bYKWP",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Essential imports\n",
- "import numpy as np\n",
- "import tensorflow as tf\n",
- "import matplotlib.pyplot as plt"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "eKpz5NCIYMdi",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Let's define some tensors\n",
- "t1 = tf.constant(2.0, dtype=tf.float32)\n",
- "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
- "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
- " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "vmMcjzTxbWzw",
- "colab_type": "code",
- "outputId": "c2901160-d845-41c1-d060-964bff742ab3",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 67
- }
- },
- "cell_type": "code",
- "source": [
- "# Let's print them out!\n",
- "print (t1)\n",
- "print (t2)\n",
- "print (t3)"
- ],
- "execution_count": 3,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Tensor(\"Const:0\", shape=(), dtype=float32)\n",
- "Tensor(\"Const_1:0\", shape=(2,), dtype=float32)\n",
- "Tensor(\"Const_2:0\", shape=(2, 3, 2), dtype=float32)\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "10ahnfjYbcop",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "Where's Waldo?
\n",
- "I mean, the value?
\n",
- "\n",
- "So, the thing is you can't print the value of tensors directly.
\n",
- "You have to use `session`, so let's do that!"
- ]
- },
- {
- "metadata": {
- "id": "ol6O5I7Tb2nb",
- "colab_type": "code",
- "outputId": "382424df-d94d-4fe8-d347-67ea7b51570d",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 202
- }
- },
- "cell_type": "code",
- "source": [
- "sess = tf.Session()\n",
- "print (sess.run(t1))\n",
- "print (\"=======================\")\n",
- "print (sess.run(t2))\n",
- "print (\"=======================\")\n",
- "print (sess.run(t3))\n",
- "sess.close()"
- ],
- "execution_count": 4,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "2.0\n",
- "=======================\n",
- "[1. 2.]\n",
- "=======================\n",
- "[[[1. 9.]\n",
- " [2. 3.]\n",
- " [4. 5.]]\n",
- "\n",
- " [[1. 9.]\n",
- " [2. 3.]\n",
- " [4. 5.]]]\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "rXKfVs_zb-kU",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "Aaahaa!! Just printed those tensors!!!
\n",
- "Feels good!
\n",
- "\n",
- "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
- "And you are still using the markdown cells for the theory ?!\n",
- "\n",
- "I am just gonna say I am a unreasonable man.
\n",
- "\n",
- "\n",
- "So, you are programming with tf.
\n",
- "What ever you do is broken down to 2 basic steps:\n",
- "- Building the computational Graph!\n",
- "- Execute that graph using `session`!\n",
- "\n",
- "That's all!\n",
- "\n",
- "
\n",
- "\n",
- "Let's compare this 2 steps with what we did above!
\n",
- "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
- "And then I executed each tensor in this graph using a `session`.\n",
- "\n",
- "That simple!\n",
- "\n",
- "
\n",
- "\n",
- "Now, let's define a few more computational graphs and execute them with sessions.\n",
- "\n",
- "Okay, to start with let's build this computational graph!\n",
- "\n",
- "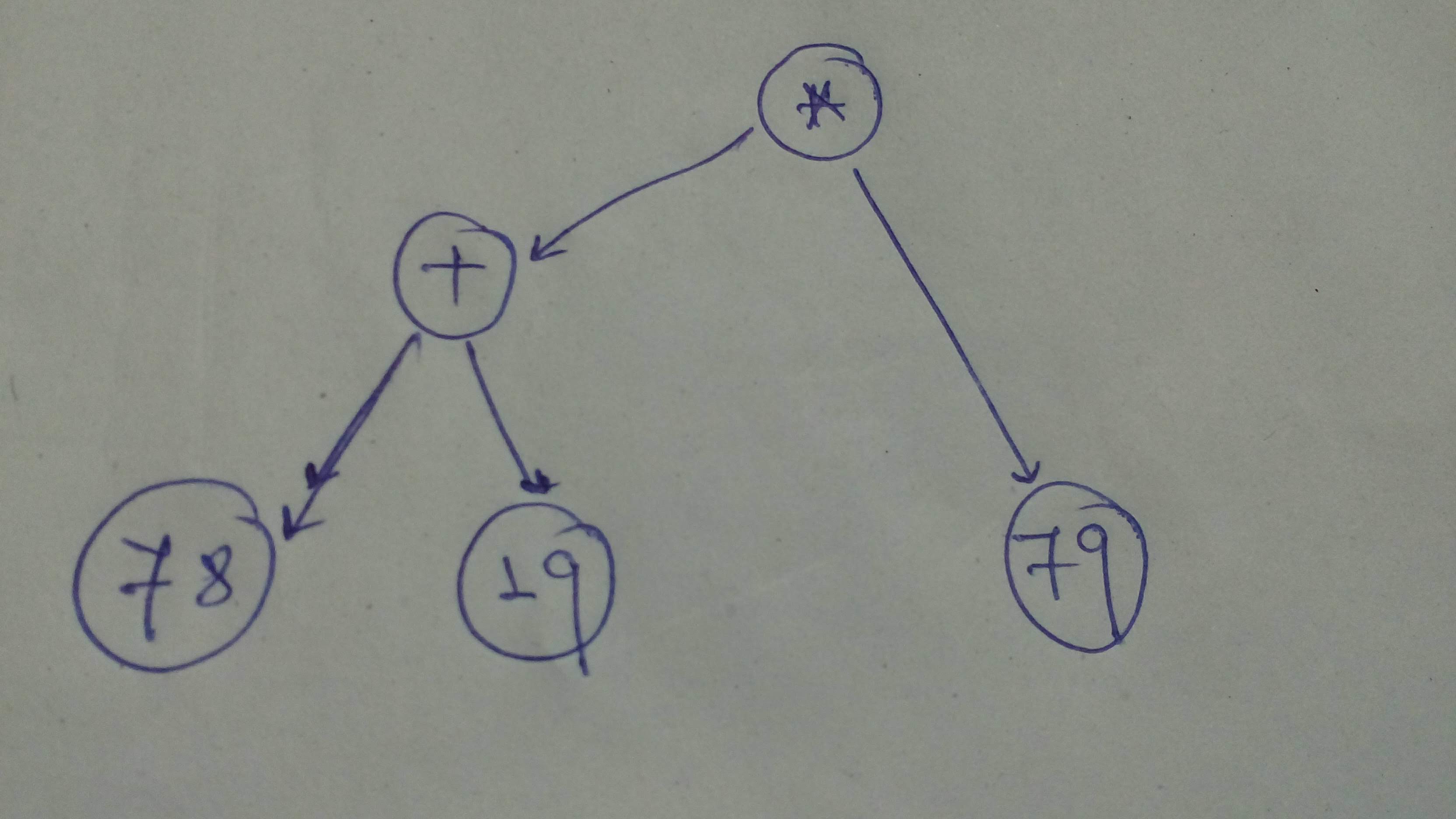"
- ]
- },
- {
- "metadata": {
- "id": "FyVz0GNqgreZ",
- "colab_type": "code",
- "outputId": "9d119dd6-c652-4e97-ea4a-0e8519f6906b",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 50
- }
- },
- "cell_type": "code",
- "source": [
- "# Let's define the graph\n",
- "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
- "\n",
- "# Alternatively\n",
- "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
- "\n",
- "# Let's execute using session\n",
- "sess = tf.Session()\n",
- "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
- "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
- "sess.close()"
- ],
- "execution_count": 5,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Comp Graph 1 : 7663\n",
- "Comp Graph 1 Alt: 7663\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "SVMMtuFYhaQB",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "Let's define a sligtly more involved graph!\n",
- "\n",
- "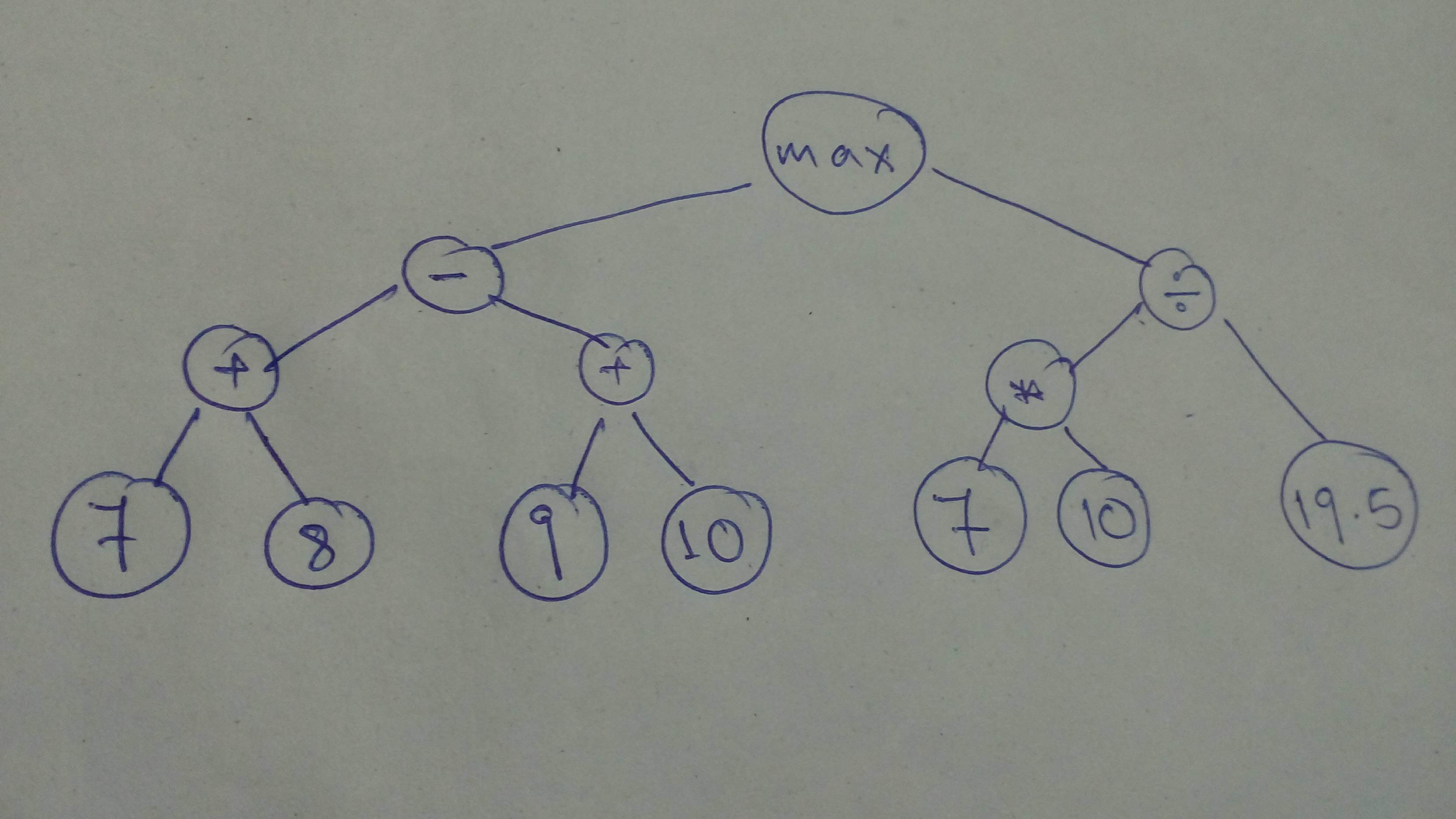"
- ]
- },
- {
- "metadata": {
- "id": "4856BTvRhiBb",
- "colab_type": "code",
- "outputId": "2d7c918b-d32d-4351-91e4-4ee318989111",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 67
- }
- },
- "cell_type": "code",
- "source": [
- "# Let build the graph\n",
- "# We need to cast cause the tensors operated on should be of the same type\n",
- "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
- " dtype=tf.float32)\n",
- "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
- "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
- "\n",
- "# Let's execute\n",
- "sess = tf.Session()\n",
- "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
- "print ('Complete Result: ', total_res)\n",
- "print ('Part 1 Result: ', part1_res)\n",
- "print ('Part 2 Result: ', part2_res)\n",
- "sess.close()"
- ],
- "execution_count": 6,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Complete Result: 3.5897436\n",
- "Part 1 Result: -4.0\n",
- "Part 2 Result: 3.5897436\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "B-_ZDtEbj4N0",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "Cool! Let's go! Build another graph and execute it with sessions.
\n",
- "\n",
- "But this time, it's all you!\n",
- "\n",
- "Build this graph and execute it with `session`!\n",
- "\n",
- "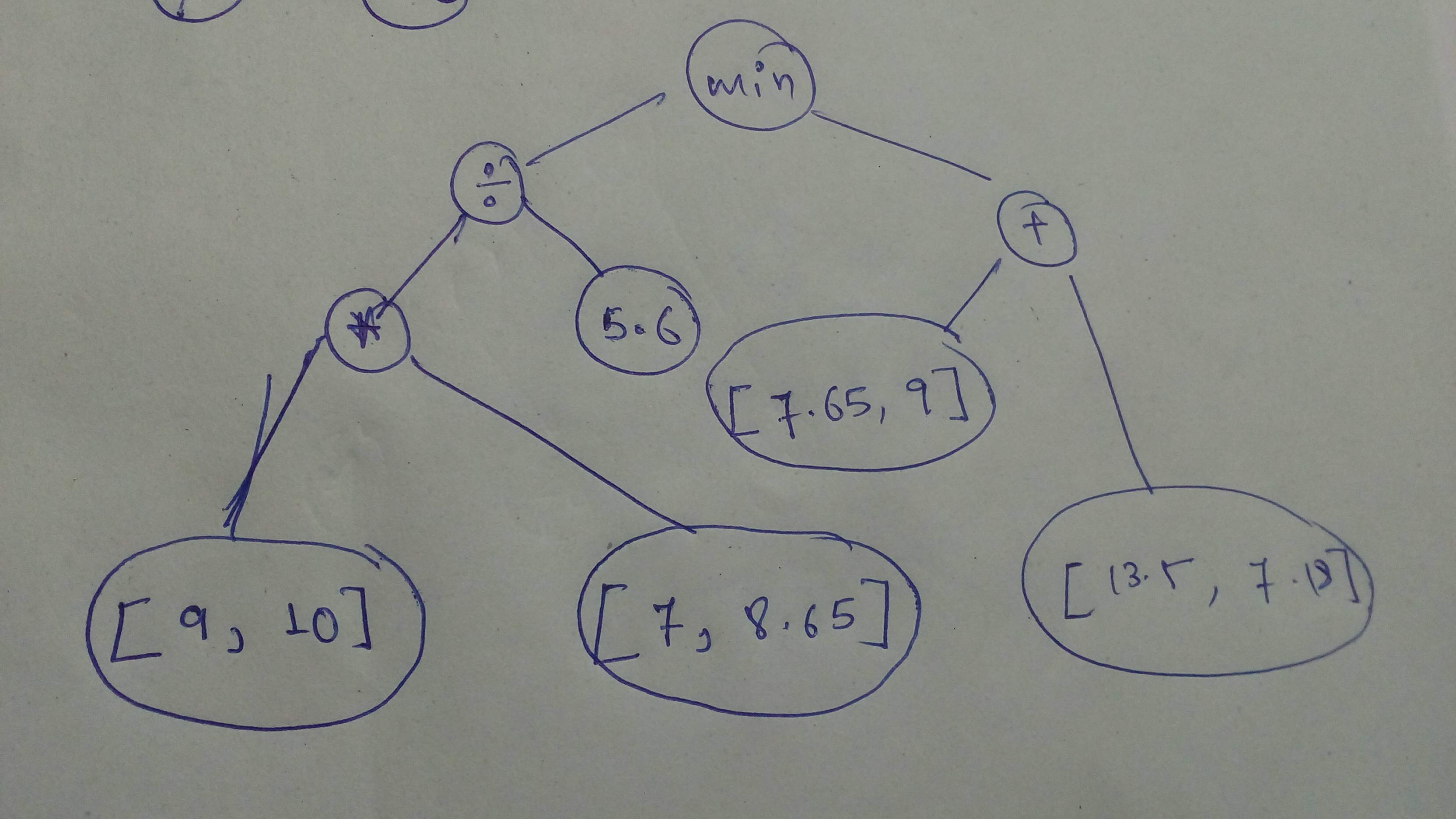\n",
- "\n",
- "_Remember that `tensors` operated on should be of the same type!_
\n",
- "_Search up errors and other help you need on Google_"
- ]
- },
- {
- "metadata": {
- "id": "-uHNe1BolJY0",
- "colab_type": "code",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 67
- },
- "outputId": "ca3885b4-428f-407d-e804-c33f2edda1ca"
- },
- "cell_type": "code",
- "source": [
- "# Build the graph\n",
- "# YOUR CODE HERE\n",
- "comp_graph_part_1 = tf.constant([9, 10], dtype=tf.float32) * tf.constant([7, 8.65], dtype=tf.float32)\n",
- "comp_graph_part_1 = comp_graph_part_1 / 5.6\n",
- "comp_graph_part_2 = tf.constant([7.65, 9], dtype=tf.float32) + tf.constant([13.5, 7.19], dtype=tf.float32)\n",
- "\n",
- "comp_graph_complete = tf.minimum(comp_graph_part_1, comp_graph_part_2)\n",
- "\n",
- "with tf.Session() as sess:\n",
- " part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
- " print ('Complete Result: ', total_res)\n",
- " print ('Part 1 Result: ', part1_res)\n",
- " print ('Part 2 Result: ', part2_res)\n",
- "# Execute \n",
- "# YOUR CODE HERE"
- ],
- "execution_count": 7,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Complete Result: [11.25 15.446429]\n",
- "Part 1 Result: [11.25 15.446429]\n",
- "Part 2 Result: [21.15 16.19]\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "qmap38WelREN",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "Let's do another!
\n",
- "It's fun! Isn't it?!\n",
- "\n",
- "Build and execute this one!\n",
- "\n",
- "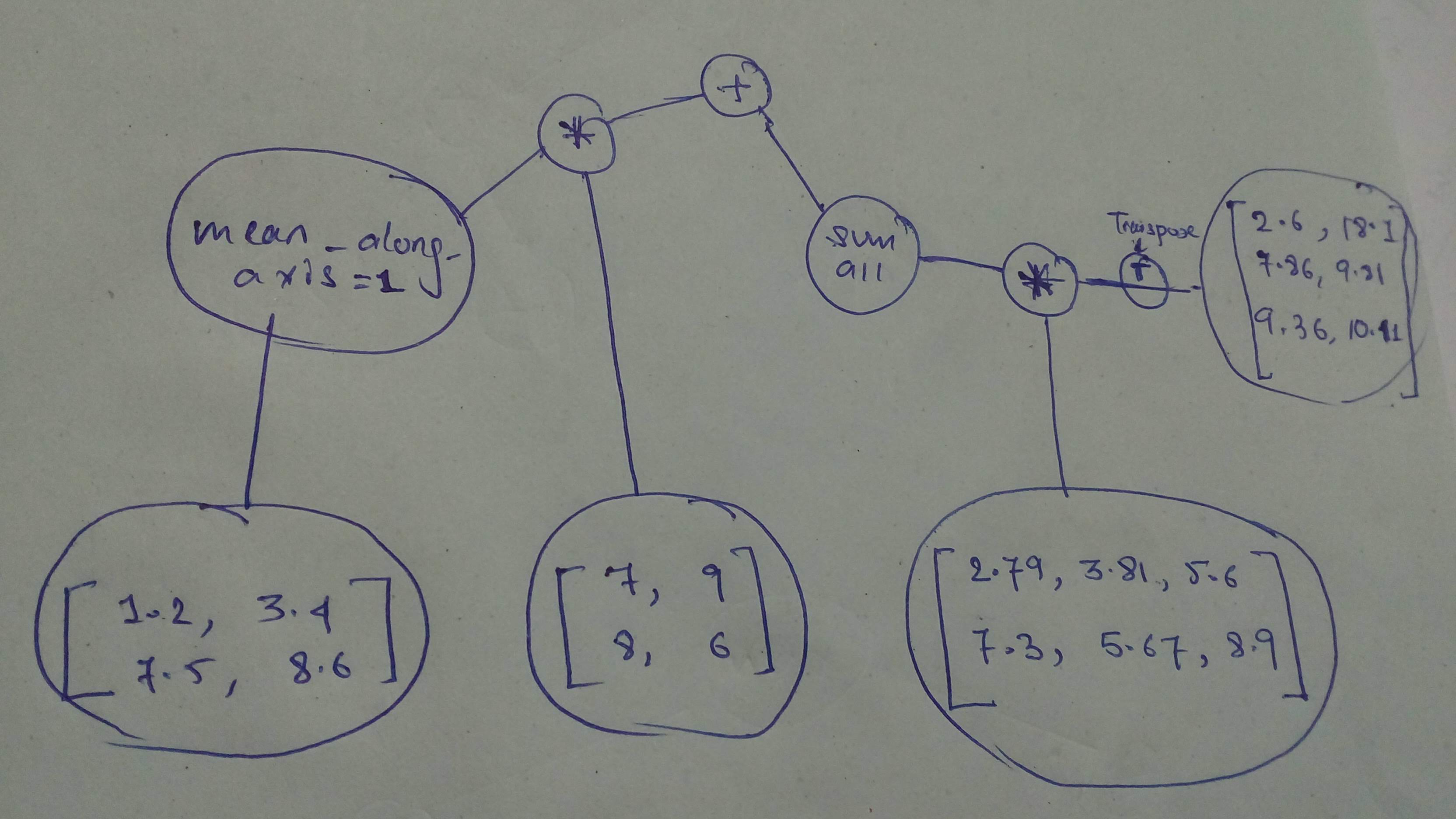"
- ]
- },
- {
- "metadata": {
- "id": "0ZhYwAlLmEvB",
- "colab_type": "code",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 151
- },
- "outputId": "6fc0f7a8-0539-40f4-cb1e-b8e730ad7662"
- },
- "cell_type": "code",
- "source": [
- "# Build the graph\n",
- "# YOUR CODE HERE\n",
- "comp_graph_part_1 = tf.constant(([7.2, 3.4],\n",
- " [7.5, 8.6]), dtype=tf.float32)\n",
- "comp_graph_part_1 = tf.reduce_mean(comp_graph_part_1, 1)\n",
- "comp_graph_part_2 = tf.constant(([7, 9],\n",
- " [8, 6]), dtype=tf.float32)\n",
- "lelf_graph = comp_graph_part_1 * comp_graph_part_2\n",
- "\n",
- "comp_graph_part_3 = tf.constant(([2.79, 3.81, 5.6],\n",
- " [7.3, 5.67, 8.9]), dtype=tf.float32)\n",
- "comp_graph_part_4 = tf.constant(([2.6, 18.1],\n",
- " [7.86, 9.81],\n",
- " [9.36, 10.11]), dtype=tf.float32)\n",
- "comp_graph_part_4 = tf.transpose(comp_graph_part_4)\n",
- "rigth_graph = tf.reduce_sum(comp_graph_part_3 * comp_graph_part_4)\n",
- "\n",
- "comp_graph_complete = lelf_graph + rigth_graph\n",
- "\n",
- "with tf.Session() as sess:\n",
- " part1_res, part2_res, total_res = sess.run([lelf_graph, rigth_graph, comp_graph_complete])\n",
- " print ('Complete Result: \\n', total_res)\n",
- " print ('Left Result: \\n', part1_res)\n",
- " print ('Rigth Result: \\n', part2_res)\n",
- "# Execute \n",
- "# YOUR CODE HERE"
- ],
- "execution_count": 8,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Complete Result: \n",
- " [[404.4483 439.7983 ]\n",
- " [409.7483 415.64832]]\n",
- "Left Result: \n",
- " [[37.100002 72.450005]\n",
- " [42.4 48.300003]]\n",
- "Rigth Result: \n",
- " 367.3483\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "BnB0b6qCmGmg",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "And a final one, before we move on to the next part!\n",
- "\n",
- "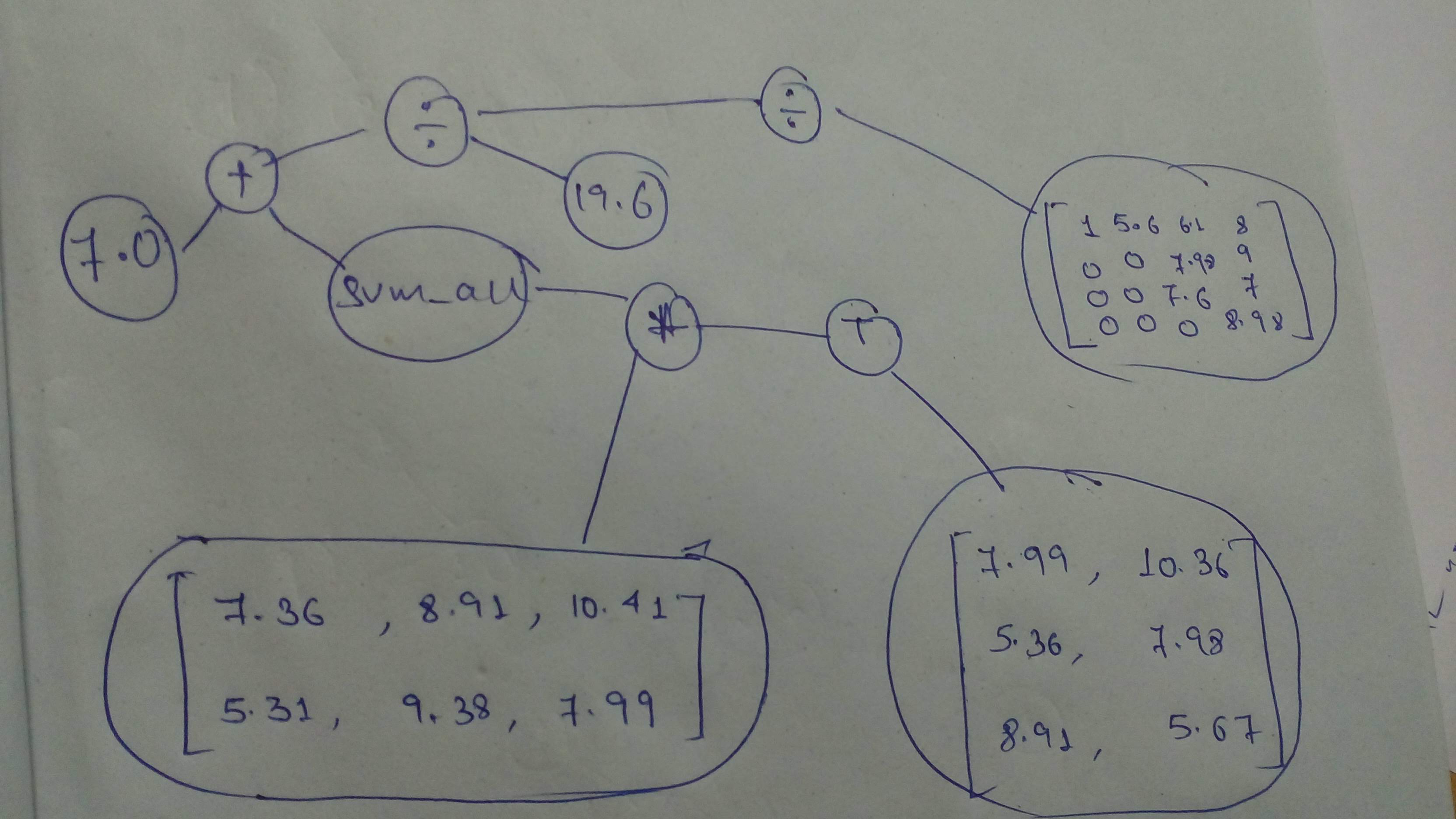"
- ]
- },
- {
- "metadata": {
- "id": "GQWyCvsQmMcL",
- "colab_type": "code",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 168
- },
- "outputId": "860c214c-c0b6-467c-c55c-11f5f3b33e06"
- },
- "cell_type": "code",
- "source": [
- "# Build the graph\n",
- "# YOUR CODE HERE\n",
- "tensor1 = tf.constant(([7.36, 8.93, 10.41],\n",
- " [5.31, 9.38, 7.99]), dtype=tf.float32)\n",
- "tensor2 = tf.constant(([7.99, 10.36],\n",
- " [5.36, 7.98],\n",
- " [8.91, 5.67]), dtype=tf.float32)\n",
- "tensor2 = tf.transpose(tensor2)\n",
- "comp_graph_part_1 = tf.reduce_sum(tensor1 * tensor2)\n",
- "\n",
- "comp_graph_part_2 = (tf.constant(7.0) + comp_graph_part_1) / 19.6\n",
- "\n",
- "comp_graph_complete = comp_graph_part_2 / tf.constant(([1, 5.6, 6.1, 8],\n",
- " [0, 0, 7.98, 9],\n",
- " [0, 0, 7.6, 7],\n",
- " [0, 0, 0, 8.98]), dtype=tf.float32)\n",
- "\n",
- "with tf.Session() as sess:\n",
- " part1_res, part2_res, total_result = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
- " print ('Total Result: \\n', total_result)\n",
- " print ('Part 1 Result: \\n', part1_res)\n",
- " print ('Part 2 Result: \\n', part2_res)\n",
- "# Execute \n",
- "# YOUR CODE HERE"
- ],
- "execution_count": 9,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Total Result: \n",
- " [[19.46896 3.4766 3.1916327 2.43362 ]\n",
- " [ inf inf 2.4397192 2.1632178]\n",
- " [ inf inf 2.5617054 2.78128 ]\n",
- " [ inf inf inf 2.1680357]]\n",
- "Part 1 Result: \n",
- " 374.5916\n",
- "Part 2 Result: \n",
- " 19.46896\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "12NC7XTPsJw7",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "# Linear Regression\n",
- "\n",
- "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
- "\n",
- "\n",
- "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
- ]
- },
- {
- "metadata": {
- "id": "hW31RZkjtNwI",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Create the dataset\n",
- "X = np.linspace(-30.0, 300.0, 300)\n",
- "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
- "\n",
- "# Normalize the dataset\n",
- "X = X / np.max(X)\n",
- "Y = Y / np.max(Y)\n",
- "\n",
- "# Divide it into train and test\n",
- "train_X = X[:250]\n",
- "train_Y = Y[:250]\n",
- "\n",
- "test_X = X[250:]\n",
- "test_Y = Y[250:]"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "LQKy6U33y4lt",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Let's define the hyperparameters\n",
- "learning_rate = 0.00001\n",
- "n_epochs = 60\n",
- "interval = 20"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "1h1-D8K1uT48",
- "colab_type": "code",
- "outputId": "497154fb-a2eb-450d-878d-484f29e9a2e9",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 347
- }
- },
- "cell_type": "code",
- "source": [
- "# let's viz the first 10 datapoints of the dataset\n",
- "plt.plot(train_X[:10], train_Y[:10], 'g')\n",
- "plt.show()"
- ],
- "execution_count": 28,
- "outputs": [
- {
- "output_type": "display_data",
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFKCAYAAADmCN3IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3XlAVOX+BvBnBhj21Qbcd0VNcQHl\nilugmFKZt8SkxCwtFbfSSkQLvWnSginirpV5DZIs85ohLogauGJkprjlisKMDrIzwJzfHya/yAUY\nB87MnOfzj3LmLN+vR33mfc+cOTJBEAQQERGRSZKLXQARERHpj0FORERkwhjkREREJoxBTkREZMIY\n5ERERCaMQU5ERGTCLMUuQB8qVb7B9+nqageNpsjg+zVm7FkapNgzIM2+2bN5UyodH7icI/K/WFpa\niF1CvWPP0iDFngFp9s2epYlBTkREZMIY5ERERCaMQU5ERGTCGOREREQmjEFORERkwhjkREREJoxB\nTkREZMIY5ERERCaMQU5ERGTCGOREREQmjEFORERkQPnaPHx75huU68rr5XgMciIiIgMRBAHT9oZh\n6t6JyFCdqJdjMsiJiIgMZNuFH/DTxW3o3bgPurt718sxGeREREQGoC5WI3z/TNha2uJz/1jIZfUT\nsQxyIiIiA5hz4F3cKrmF8F7vo7Vzm3o7LoOciIjoMe24uB0/nN8CH49eeNNrUr0em0FORET0GDQl\nt/FuyluwtrDG0oAVsJBb1OvxGeRERESPYe7BcKiKc/Buzwi0c21f78dnkBMREelp16VEJJyNRzdl\nd4R1mypKDQxyIiIiPeSV3sE7KW/BSm6FpQErYSm3FKUOvY5aVlaG8PBwZGVlwcLCAosWLUKzZs2q\nrLNt2zZs2LABcrkcI0eORHBwMIqKihAeHg61Wg1bW1tERUVBqVTizJkzmDdvHgDA09MT8+fPf+zG\niIiI6lJk6hzcKMzCrF5z0LFBJ9Hq0GtEvn37djg5OSEuLg4TJ05EdHR0ldeLioqwfPlyfPXVV9i4\ncSM2bNiA3NxcbN68Gc2aNcM333yDSZMmISYmBgCwcOFCREREID4+HgUFBUhJSXn8zoiIiOpI8pU9\n2HT6a3R+wgvTus8QtRa9gjwtLQ2BgYEAAD8/P6Snp1d5PSMjA126dIGjoyNsbGzQo0cPpKen49Kl\nS/Dy8gIA+Pj44Pjx49Bqtbh+/Xrlcn9/f6SlpT1OT0RERHWmQJuPmfumwVJuiaX+y2FlYSVqPXoF\nuVqthpub290dyOWQyWTQarUPfB0A3NzcoFKp0L59+8rR9pEjR5CVlQWNRgMnJ6fKdRs0aACVSqVX\nM0RERHXtP2kf4FrBVUzr/ja6KLuKXU7118gTEhKQkJBQZVlGRkaVnwVBeOQ+7r0+YsQIZGZmIiQk\nBL169aoS9jXdFwC4utrB0tLw9+kplY4G36exY8/SIMWeAWn2zZ7rVvKfyfjq1Ho8qXwSHw35ENaW\n1vV27IepNsiDg4MRHBxcZVl4eDhUKhU6dOiAsrIyCIIAhUJR+bq7uzvUanXlzzk5OejWrRsUCkXl\nB9kKCwuxZ88euLm5ITc3t3Ld7OxsuLu7P7ImjaaoZt3VglLpCJUq3+D7NWbsWRqk2DMgzb7Zc90q\nLCvEa1tfh1wmx+L+scjTaAFoq93OUB72hkWvqfU+ffogMTERAJCcnAxfX98qr3ft2hUnT55EXl4e\nCgsLkZ6eDh8fH6SkpGDJkiUA7n6qvV+/frCyskLr1q1x7NgxAEBSUhL69eunT1lERER15qND83E5\n7xLCuk1Dd4/6ebJZTeh1+1lQUBBSU1MREhIChUKBqKgoAMCaNWvQs2dPdO/eHTNnzsS4ceMgk8kw\nefJkODo6wtfXF5s2bcLIkSPh7OyMxYsXAwAiIiLwwQcfQKfToWvXrvDz8zNch0RERI/p0I00rDu5\nGm1d2uG9nhFil1OFTKjJRWkjUxfTKJySkgb2LB1S7Js9143i8mIEbO6Di7kX8L9/J6FXI9/qN6oD\nBp1aJyIikoqPjyzEhdzzeLNrmGgh/igMciIiooc4nn0UqzJi0dKpFWb3el/sch6IQU5ERPQApRWl\nmL43DDpBhyX+y2FnZSd2SQ/EICciInqA6KMf46wmE693fgN+TfqKXc5DMciJiIj+ISPnBJad+BzN\nHJtjbm/jfpAXg5yIiOhvtBVaTNsbhgqhAoufWgYHKwexS3okBjkREdHfLE2PxunbpxDaaSwGNPMX\nu5xqMciJiIj+ckr9Oz4//ika2zdBZO8PxS6nRhjkREREAMoqyjA9OQzlunJEP7UUTtbOYpdUIwxy\nIiIiAMt/XYrfVL/iJc+XMbDFYLHLqTEGORERSV7m7TP47GgUPOwa4sM+i8Qup1YY5EREJGkVugq8\nlRwGrU6LTwcsgYuNq9gl1QqDnIiIJG1VxnIczz6GF9oFY0irILHLqTUGORERSdaF3HP4+MgCPGGr\nxEf9PhG7HL3o9TxyIiIiU6cTdJi+dzJKKkqwvP8auNk0ELskvXBETkREkrT+5GocuXkIz7UZjufa\nDBe7HL0xyImISHL+vHMRCw/Nh5uNG6L6RYtdzmPh1DoREUmKTtBhRvJUFJUXYbH/MijtlGKX9Fg4\nIiciIkn5+tSX+CXrAIa0DMK/244Qu5zHxiAnIiLJuJp/BfPT3oeztQs+HbAEMplM7JIeG6fWiYhI\nEgRBwIzkqSgsK0BMwEp42DcUuySD4IiciIgk4ZvTG5FyLRkDmwfiJc+XxS7HYBjkRERk9rIKruOD\n1Ag4WDniswFLzWJK/R5OrRMRkVkTBAHv7JuOfG0eop+KQRPHpmKXZFAckRMRkVlLOBuP3VeS0L+p\nP0Z3fFXscgyOQU5ERGYru/Am5h6cBTtLeyx+KsasptTv4dQ6ERGZJUEQ8N7+GcgtzcWifp+huVML\nsUuqExyRExGRWfrx/Pf4+c/t8GvcF691Hi92OXWGQU5ERGZHXazG7APvwNbSFov9l0EuM9+4M9/O\niIhIsmbvfwe3Sm4hwvcDtHZuI3Y5dYpBTkREZmX7hW348cL38PHohfFdJopdTp1jkBMRkdm4XXIL\ns/bPgLWFNZYGrICF3ELskuocg5yISCIOXt+PT48uwklVhtil1Jm5B8OhKs7Be73moJ1re7HLqRe8\n/YyIyMyV68oRdXgBYk4sBgB8enQRvJTd8ErHMXih3Qg4W7uIXKFhJF36Gd+d/Rbd3XtgUtcpYpdT\nbzgiJyIyY9fzr2H41iDEnFiMFk4t8flTsRjSMgin1Ccxa/8MdPmqPSbvfhOp1w9CEASxy9XbndJc\nvJPyFqzkVljivwKWcumMU6XTKRGRxOy89DOm7ZkITakGz7d5AdFPLYWTtTNe6TQG2YU38W3mN9h0\n+msknI1Hwtl4tHZug5c7jsFLHV6Gh52H2OXXSuQvc3Cz8AbCe81FxwadxC6nXskEPd6ClZWVITw8\nHFlZWbCwsMCiRYvQrFmzKuts27YNGzZsgFwux8iRIxEcHIyioiKEh4dDrVbD1tYWUVFRUCqVCA0N\nRVFREezs7AAAs2bNQufOnR96fJUqv7YlV0updKyT/Roz9iwNUuwZkGbf93rWVmix4NA8rMqIhbWF\nNRb0/RhjOr32wK8nFQQBaVm/4L+nN2D7hR9RUlECC5kFAlsOwSsdx2Bg80CjHt0qlY749vgPGLX9\nBXR5oisSX9wLKwsrscuqE0ql4wOX63V2tm/fDicnJ0RHR+PgwYOIjo7GkiVLKl8vKirC8uXL8d13\n38HKygojRoxAYGAgtm7dimbNmiEmJgbHjh1DTEwMPvzwQwDAokWL0L69ND6YQERUVy7nXcKEpNeQ\nnnMcbV3aYe3gDXjyiYcPjGQyGfya9IVfk75Y1O9TbDmXgE1/fI3EP39C4p8/wcOuIUI6jEZIx9Fo\n5dy6HjupmbzSPMzcNw2WckssCVhutiH+KHpdI09LS0NgYCAAwM/PD+np6VVez8jIQJcuXeDo6Agb\nGxv06NED6enpuHTpEry8vAAAPj4+OH78+GOWT0RE93x/+nsM3NwP6TnHEdx+FJKCUx4Z4v/kbO2C\n1zu/gT0jD2B38H681nk8isuLsST9M/hu6oYXfnwWW85uRkl5SR12UTvv7XoP1wuuYVqPGejyhJfY\n5YhCrxG5Wq2Gm5sbAEAul0Mmk0Gr1UKhUNz3OgC4ublBpVKhffv2SElJwdNPP40jR44gKyurcp2Y\nmBhoNBq0adMGERERsLGxeejxXV3tYGlp+HsDHzZtYc7YszRIsWdAOn2XlJfg3aR3EXs0FraWtvhi\n2BcY223sYz3pa6CyHwZ26ofYsqX4/vT3WJe+DimXU3Dw+n642LhgdJfRGN9jPLo27GrATmpn7597\nsfr4anR274xFQz6EwkIhWi1iqjbIExISkJCQUGVZRkbVexCru8x+7/URI0YgMzMTISEh6NWrV2XY\njxkzBp6enmjevDkiIyOxadMmjBs37qH702iKqiu71qR8PU1K2LN0SKXvi7nn8UbSazipzsCTyiex\nauCX8HTrALW6wGDHeLrR83j6medxMfc8vjn9X8RnbkLs0VjEHo1FV2X3ytvYnKydDXbM6hSUFeC1\nreNgIbPA4v6xuHO7FEBpvR1fDHpfIw8ODkZwcHCVZeHh4VCpVOjQoQPKysogCELlaBwA3N3doVar\nK3/OyclBt27doFAoMH/+fABAYWEh9uzZAwCV0/QAEBAQgB07dtSiNSIiafr+XAJm7puOwrICjO74\nKlb/ewUKcyvq7HitXdpibu95mNVrDvZc2YVNpzdg9+UkvLf/bUSmRuC5NsMxuuOr8G3Uu86f+/3R\nofm4kncJ4X3C0c29R50ey9jpdY28T58+SExMBAAkJyfD19e3yutdu3bFyZMnkZeXh8LCQqSnp8PH\nxwcpKSmVH4rbtm0b+vXrB0EQMHbsWOTl5QEADh8+jHbt2j1OT0REZq24vBgz903DxF13Zy5XDlqH\nxf7LYGdlVy/Ht7KwwpBWQdgY9C1OjPkDc3wj4WHXEJsz4zBs6xD4xXlj2YklyCnKqZPjH8pKxbqT\nq9HOpT0in4qsk2OYEr1uP6uoqMDcuXNx6dIlKBQKREVFoVGjRlizZg169uyJ7t27IzExEevXr4dM\nJsPo0aMxbNgwlJSUYNq0acjNzYWzszMWL14MR0dH7NixA+vWrYOtrS08PDywcOFC2NraPvT4vP3M\nMNizNEixZ8B8+z57OxNvJL2K07f/wJMNumDd01+hjcvdwY+YPesE3d3b2P7YgJ8ubkNJRQks5ZYI\nbDEEozuOgX/zQQa5ja2orAj+m/1w6c6f2P5CEoK6DDLL8/wgD5ta1yvIxcYgNwz2LA1S7Bkwz77j\nz2xC+P6ZKCovwmudx2O+30ewsfz/DwYbS8+5JZq7t7Gd/hq/q38DADSyb4xRHV5GSIdQtHRupfe+\nI3+Zg5UZyzCx6xT8p89HRtNzfWCQV0NKfxnuYc/SIMWeAfPqu6CsAOH7Z2JzZhwcFU5Y4h+L59oM\nv289Y+z5N9Wv+O8fG7DlXALytXcvofZr+hRe6RiKoFbPVXkjUp1jN4/g2R8Go4VTSySPTIWdlZ1R\n9lxXDPqFMEREVD/+uHUKb+x8Fedyz6KbsjvWDP7qsUa09c1L2Q2fDOiGeX4Lsf3ij9h0+mscuLYP\nB67tg4u1C4Lbj8LLHcdUe797SXkJpu8Ng07QYYn/8nr7PIAp4ENTiIiMkCAI2PjHVxjynT/O5Z7F\nBK8wbH9hl0mF+N/ZWdlhpGcIfhz+M9JePo6p3d+GlVyBtSdXwX+zH57+7ilsOPVF5aj9n6KPfYxz\nuWcxrsub6N24Tz1Xb9w4tf4XKU3P3MOepUGKPQOm3Xe+Ng/v7JuOH85vgYu1C2ICVmFIq6BqtzO1\nnssqyrD7ShI2/bEBu68kQSfoYGdph2Ft/41XOr6KXg19IZPJkJFzAkO2BKCJYzPseykVDlYOlfsw\ntZ4fB6fWiYhMwG+qX/FG0lj8eecifDx6Yc3gL9HUsVn1G5ogKwsrDG31DIa2egY3CrIqn8YWf2YT\n4s9sQluXdnil46vYnBmHCqECi5+KqRLidBen1omIjIAgCFh/cjWCtgzCn3cuYmr3t/Hj8J/NNsT/\nqZFDY7zl/Q4Ov/Irvn9+O15oF4yr+VcwP20uTt8+hdBOr6F/06fELtMocURORCSyO6W5eCt5Cn66\nuA0NbBpg+aA1CGgeWP2GZkguk6Nvk/7o26Q/NCW38f25BGTePoP3e88XuzSjxSAnIhLR8eyjmJD0\nOq7kX0bvxn2watB6NHJoLHZZRsHVxg3jukwQuwyjx6l1IiIRCIKAFb8uw3M/PI2r+Vcw02cWtgz7\nH0Ocao0jciKiena75Bam7ZmEpMuJUNq6Y2XgOl7/Jb0xyImI6tHhG4cwIek1ZBVeR/+m/lgxaC3c\n7dzFLotMGIOciKge6AQdlqV/jqgjCyBAwOxe72NajxmwkFuIXRqZOAY5EVEdUxWpMHnPG9h3dS8a\n2TfG6sAv8K/GfmKXRWaCQU5EVIcOXt+PibvGIacoGwObByJ24Bo0sG0gdllkRhjkRER1oEJXgcXH\nP0H0sY8hl8kR2XsBJnWbArmMNwuRYTHIiYgM7GbhDYTtfgMHr+9HM8fmWB34BXwa9hK7LDJTDHIi\nIgNKvrIHk/e8AXWxGkNbPYul/svhYuMqdllkxhjkREQGUK4rx8dHFmJpejSs5FZY2PdjjO8yETKZ\nTOzSyMwxyImIHtP1/GuYsOt1HLl5CC2cWmLt4K/Qzb2H2GWRRDDIiYgeQ9KlnzF1z0RoSjV4vs0L\niH5qKZysncUuiySEQU5EpAdthRYLDs3DqoxYWFtY49MBSzCm02ucSqd6xyAnIqqFzNtnsDkzDlvO\nbkZW4XW0cWmLtYM3oPMTXcQujSSKQU5EVA1VkQo/nEvA5rPx+E31KwDASeGM8V0mIOJfkXCwchC5\nQpIyBjkR0QMUlxdj5587kHA2Hnuv7EaFUAFLuSUGtxiCkZ4hGNxyKGwsbcQuk4hBTkR0j07Q4fCN\nNCRkxuPHCz8gX5sHAOim7I5gz1EY3nYElHZKkaskqopBTkSSdyH3HBIy4/Hd2c24kn8ZANDYvgle\ne3I8gj1HwdOtg8gVEj0cg5yIJOl2yS1sPf89EjLjcDz7GADA3soBozq8guD2o9CnST9+LzqZBAY5\nEUlGaUUpdl9OwubMOOy+vBNlujLIZXL4NxuIkZ4hGNLqGdhb2YtdJlGtMMiJyKwJgoBj2UeQkBmP\nree3ILc0FwDQqUFnjPQMwYvtguFh31DkKon0xyAnIrN0UXMRq4+uR8LZePx55yIAwN3OA5O6TkWw\n5yje901mg0FORGbjTmkutl3Yis2ZcTh8Iw0AYGtpixfbjUSw5yj0b/oULOX8b4/MC/9GE5FJK6so\nQ/LV3dicGY+dl3agtKIUMsgQ0CoAw1sF49nWw+CgcBS7TKI6wyAnIpMjCAIyVCeQkBmPH85/B3Wx\nGgDQ3tXzr+veI9GtdUeoVPkiV0pU9xjkRGQyruVfxZazm5FwNh5nNZkAgAY2DfBGl4kY6RkCL2U3\nPrSEJIdBTkRGrUCbj+0Xt2FzZhx+uX4AAgRYW1hjWJt/Y6TnKPg3GwQrCyuxyyQSjV5BXlZWhvDw\ncGRlZcHCwgKLFi1Cs2bNqqxz584dzJgxA/b29oiJiXnkdmfOnMG8efMAAJ6enpg/f/7jdUVEJq1c\nV47915KxOTMeP/+5HcXlxQCAfzXyQ7DnKAxrMxzO1i4iV0lkHPT62qLt27fDyckJcXFxmDhxIqKj\no+9bJzIyEt7e3jXabuHChYiIiEB8fDwKCgqQkpKiT1lEZOJ+V59E5C9z0O3rjhi1/UV8fy4BDe0b\nYVavOTg6+jds+3ciQjuNZYgT/Y1eI/K0tDQMHz4cAODn54eIiIj71lmwYAFOnTqFM2fOPHI7rVaL\n69evw8vLCwDg7++PtLQ0DBgwQJ/SiMiIVegqoC5RQ1WUg5yibOQUZUNVrEJOUTYOXEvBH7d+BwC4\nWLtg7JPjEOw5Cj4evXjdm+gR9ApytVoNNzc3AIBcLodMJoNWq4VCoahcx8Hh/ufzPmg7tVoNJyen\nynUaNGgAlUqlT1lEJAKdoIOmRANV8d/CuUj1t6DOQU5RDlRFObhVooZO0D1wP1ZyKwxt9SxGeoZg\nUIvBsLawrudOiExTtUGekJCAhISEKssyMjKq/CwIgl4Hf9B2NdmXq6sdLC0t9DrmoyiV0rvXlD1L\nQ217FgQBd0rvILsgGzcLbuJmwU1kF97/++yCbGQXZqNcV/7I/TkqHNHQoSE8le3R0KEhGto3hIeD\nBxo6NISH/d1f27q1haut6+O0eR+ea2mQYs9/V22QBwcHIzg4uMqy8PBwqFQqdOjQAWVlZRAEocpo\n/GHc3d3v206pVCI3N7dynezsbLi7uz9yPxpNUbXHqi2l0lFy95yyZ2n4e88FZQV/TWvn/G20nA3V\nXyPmv091l1aUPnK/tpa2UNp5oJuyB5R27nC384DSVgl3O4+7v7dT/rXMHXZWdtXWWV4AqAoMd26k\nfq6lQko9P+wNi15T63369EFiYiL69euH5ORk+Pr66r2dlZUVWrdujWPHjsHHxwdJSUkIDQ3Vpywi\nAnAi+zj2XNlVGcqaMjWy7txATlEOisoLH7mtQq6A0s4dnRo8WRnC7nbu/x/Udh5w/yus7a0ceO2a\nyAjoFeRBQUFITU1FSEgIFAoFoqKiAABr1qxBz5494eXlhbFjxyIvLw/Z2dkIDQ1FWFjYQ7eLiIjA\nBx98AJ1Oh65du8LPz89wHRJJyOlbf2DY1iFVRtMWMgso7dzRxqUt3CtHzlUD+t5o2tnaheFMZGJk\ngr4XuEVUF9MoUpqeuYc9m5fSilI8/Z0//rj1Oz7p/zl8G/WG0s4dns1a4Jb60SNxc2TO5/ph2LN5\nM+jUOhEZn48O/Qd/3PodYzq9jrGdx1Uul8v0+roIIjIR/BdOZAb2X9uHlRnL0MalLeb3WSh2OURU\njxjkRCZOU3IbU/dMhKXcEisHrYO9lb3YJRFRPWKQE5kwQRDwbsrbuFGYhfd6RqCbew+xSyKiesYg\nJzJhmzPjsO3CD/Bt1BtTu78tdjlEJAIGOZGJupx3CbMPvAsHK0csH7gGFnLDf9shERk/fmqdyASV\n68oxefebKCjLR+zA1Wju1ELskohIJByRE5mgmPTFOHLzEIa3fQHB7UeJXQ4RiYhBTmRi0rOP4dOj\ni9DYvgk+6f85v4mNSOIY5EQmpKCsAGG734BO0CF20Gq42Bj2aWFEZHoY5EQmJPKXObh45wImdZuK\nvk36i10OERkBBjmRifj5z5+w8Y8v8WSDLpjt+77Y5RCRkWCQE5mA7KJszEieAhsLG6wMXAdrC2ux\nSyIiI8Hbz4iMnCAImL53Em6V3MJHfT9BB7eOYpdEREaEI3IiI/fF72ux98pu+DcbiHFdJohdDhEZ\nGQY5kRHLvH0G81Pnws3GDTEBK3mrGRHdh1PrREZKW6HFpN3jUVJRglWBX8DDvqHYJRGREeKInMhI\nRR1ZgN/Vv2F0x1cR1PpZscshIiPFICcyQr9cP4DlJ5ailXNr/KfvIrHLISIjxiAnMjK5JRpM2TMB\ncpkcKwathYOVg9glEZERY5ATGZnwAzNxveAaZvrMgrdHT7HLISIjxyAnMiLfnf0W35/7Dj4evfCW\n9ztil0NEJoBBTmQkruZfwaz9M2Fv5YAVg9bCUs6bSoioevyfgsgIVOgqMHn3m8jX5iEmYCVaOrcS\nuyQiMhEckRMZgeW/LsWhG6l4rs1wvOT5stjlEJEJYZATiSwj5wSijixAQ/tG+HTA5/z2NiKqFQY5\nkYiKyoowafd4lOvKsSxgFdxsGohdEhGZGAY5kYjmpc7B+dxzmNB1MgY08xe7HCIyQQxyIpHsupSI\nr06tR0e3JzHHN1LscojIRDHIiUSgKlJhevJkWFtYY2XgOthY2ohdEhGZKN5+RlTPBEHA28mToS5W\n4cM+i9CpwZNil0REJowjcqJ6tuHUF0i6nIj+Tf3xhtckscshIhPHICeqR+c15xCZGgFXa1fEDlwF\nuYz/BIno8XBqnaieaCu0mLR7PIrLixE7cA0a2jcSuyQiMgMcDhDVk8+ORiFDdQIhHUbjuTbPi10O\nEZkJBjlRPTiUlYql6dFo4dQSC/t+LHY5RGRG9JpaLysrQ3h4OLKysmBhYYFFixahWbNmVda5c+cO\nZsyYAXt7e8TExDxyu9DQUBQVFcHOzg4AMGvWLHTu3PkxWyMyDnmldzB5z5uQyWRYMWgtHBSOYpdE\nRGZErxH59u3b4eTkhLi4OEycOBHR0dH3rRMZGQlvb+8ab7do0SJs3LgRGzduZIiTWQk/8A6u5l/B\n297vomdDX7HLISIzo1eQp6WlITAwEADg5+eH9PT0+9ZZsGDBfUFek+2IzMkP577Dd2e/hbeHD2Z4\nvyd2OURkhvSaWler1XBzcwMAyOVyyGQyaLVaKBSKynUcHBxqvB0AxMTEQKPRoE2bNoiIiICNDb/p\nikzb9fxreG//DNhZ2mP5oLWwsrASuyQiMkPVBnlCQgISEhKqLMvIyKjysyAIeh383nZjxoyBp6cn\nmjdvjsjISGzatAnjxo176HaurnawtLTQ65iPolRK79ole64bOkGHkTvCcKc0F+ueWwfftt3q/JiP\nIsXzDEizb/YsPdUGeXBwMIKDg6ssCw8Ph0qlQocOHVBWVgZBEKqMxh/G3d39gdvdm24HgICAAOzY\nseOR+9Foiqo9Vm0plY5QqfINvl9jxp7rTuyJpdh3aR+GtnoWzzUNFvXPWYrnGZBm3+zZvD3sDYte\n18j79OmDxMREAEBycjJ8fWv2AZ4HbScIAsaOHYu8vDwAwOHDh9GuXTt9yiIyCifVv2HR4f/A3c4D\ni59aBplMJnZJRGTG9LpGHhQUhNTUVISEhEChUCAqKgoAsGbNGvTs2RNeXl6V4ZydnY3Q0FCEhYU9\ncDuZTIaRI0di7NixsLW1hYeHB6ZOnWrQJonqS3F5MSbtGocyXRliAlaigW0DsUsiIjMnE/S9wC2i\nuphGkdL0zD3s2fAiDryLdSckA+ExAAAaSUlEQVRX440uE7Gw3yd1dpzakOJ5BqTZN3s2bwadWiei\n++29sgvrTq5GB7eOmNt7vtjlEJFEMMiJDEBdrMa0vWFQyBVYMWgdbC1txS6JiCSCQU70mARBwIx9\nU5FTlI3Zvh+g8xNdxC6JiCSEQU70mDad/hqJf/6Evk36Y1K3KWKXQ0QSwyAnegwXc89j7sFZcLZ2\nwbKAVZDL+E+KiOqXXrefERFQVlGGsN1voKi8CGsDVqCJY1OxSyIiCeLwgUhP0cc/RnrOcQS3H4Xn\n274gdjlEJFEMciI9HLlxGEuOf4bmji0Q1f8zscshIgljkBPVUr42D2F73gAAxA5aA0eFk8gVEZGU\nMciJamnOwVm4kncJ03vMwL8a9Ra7HCKSOAY5US3878JWxJ/ZhG7K7njHZ7bY5RARMciJaupGQRZm\n7psGO0s7rAxcBysLK7FLIiLi7WdENaETdJiydyJyS3Px6YAlaOPCR+0SkXHgiJyoBtb8tgIHru3D\n0y2HYkyn18Quh4ioEoOcqBqn1L9jQdo8PGGrxOKnYiGTycQuiYioEoOc6BFKyksQtns8tDotYgJW\nQGmnFLskIqIqGOREj7Dw0Dycvv0HXus8HoNaPC12OURE92GQEz1E8pU9WP3bCrRzaY/I3gvELoeI\n6IEY5EQPcKv4FqbtnQQruRVWBq6DnZWd2CURET0Qg5zoHwRBwIx9U5FddBPhvu/DS9lN7JKIiB6K\nQU70D5tOf42f/9yOvk36Y3K3aWKXQ0T0SAxyor+5kHsOcw/OgrO1C5YFrIJcxn8iRGTc+M1uRH8p\nqyhD2O43UFRehLUBK9DEsanYJRERVYvDDaK/fHZsEU7kpOMlz5fxfNsXxC6HiKhGGOREAA5lpWLJ\n8Wg0d2qJj/p9InY5REQ1xiAnybtTmouw3W9ALpNj5aC1cFQ4iV0SEVGNMchJ8mbtn4lrBVfxtve7\n6NnQV+xyiIhqhUFOkvbd2W/x/bkEeHv0xAyf98Quh4io1hjkJFlX8i5j1v6ZsLdywIpBa2Ep500c\nRGR6+D8XSVKFrgJT9kxAvjYPMQEr0cq5tdglERHphSNykqRlJz7HoRupGNbm33jJ82WxyyEi0huD\nnCTnRPZxfHL0IzSyb4xPB3wOmUwmdklERHpjkJOkFGgLMGn3eFToKrB80Bq42riJXRIR0WNhkJOk\nvJ34Ni7euYCwbtPQt0l/scshInpsDHKSjJ8u/g/rTqxD5ye8EO47V+xyiIgMgkFOknCz8AZmJE+B\njaUNVg1aD2sLa7FLIiIyCL2CvKysDDNnzkRISAhGjx6Nq1ev3rfOnTt3MG7cOEybVvV5zkeOHEHv\n3r2RnJxcuezMmTMYNWoURo0ahcjISH1KInoonaDD1D0ToSnVIHpwNNq7eYpdEhGRwegV5Nu3b4eT\nkxPi4uIwceJEREdH37dOZGQkvL29qyy7cuUKvvzyS/To0aPK8oULFyIiIgLx8fEoKChASkqKPmUR\nPdDa31Yi5VoyAls8jUk+k8Quh4jIoPQK8rS0NAQGBgIA/Pz8kJ6eft86CxYsuC/IlUolYmNj4ejo\nWLlMq9Xi+vXr8PLyAgD4+/sjLS1Nn7KI7nNK/Ts+TIvEE7ZKLPFfwVvNiMjs6BXkarUabm53b9uR\ny+WQyWTQarVV1nFwcLhvO1tbW1hYWFRZptFo4OT0/0+batCgAVQqlT5lEVVRXF6MsN3jodVpEROw\nAko7pdglEREZXLVf0ZqQkICEhIQqyzIyMqr8LAiCwQqqyb5cXe1gaWlR7Xq1pVQ6Vr+SmTHnnqf/\nPBenb/+ByT0nI8RnROVyc+75YaTYMyDNvtmz9FQb5MHBwQgODq6yLDw8HCqVCh06dEBZWRkEQYBC\nodCrADc3N+Tm5lb+nJ2dDXd390duo9EU6XWsR1EqHaFS5Rt8v8bMnHvee2UXYo7EoL2rJ97r/kFl\nn+bc88NIsWdAmn2zZ/P2sDcsek2t9+nTB4mJiQCA5ORk+Prq/wxnKysrtG7dGseOHQMAJCUloV+/\nfnrvj0hdrMbUPZNgJbfCysD1sLW0FbskIqI6o9fTz4KCgpCamoqQkBAoFApERUUBANasWYOePXvC\ny8sLY8eORV5eHrKzsxEaGoqwsDCUlpZi/fr1uHjxIk6dOoWNGzfiiy++QEREBD744APodDp07doV\nfn5+Bm2SpEMQBMxIngJVcQ4iey9Alye8xC6JiKhOyQRDXuCuJ3UxjSKl6Zl7zLHnr099iXdSpqNf\nkwFIGPYj5LKqk07m2HN1pNgzIM2+2bN5M+jUOpExOq85h/d/CYeLtQuWDVx1X4gTEZkjvabWiYyN\ntkKLSbvHo7i8GLEDV6OxQxOxSyIiqhccspBZ+OTIR8hQnUBIh9F4rs1wscshIqo3DHIyeanXD2LZ\nic/R0qkVFvb9WOxyiIjqFYOcTFpuiQaT97wJuUyOFYPWwkEh7S+GICLpYZCTyRIEAbP2z8D1gmuY\n6TMLPg17iV0SEVG9Y5CTyfru7Lf44fwW9Gzoi7e83xG7HCIiUTDIySRdzruEWftnwsHKEcsHroGl\nnDdgEJE08X8/MjnlunJM3v0mCsrysSxgFVo6txK7JCIi0XBETiZnaXo0jtw8hOFtX8BIzxCxyyEi\nEhWDnEzK8eyj+OxoFJo4NMUn/T+HTCYTuyQiIlExyMlkFGjzMWnXeOgEHWIHroaLjavYJRERiY5B\nTiZj7sFwXMr7E1O6v4U+TfioWyIigEFOJuJ/F37EN2c2wkvZDbN6zRG7HCIio8EgJ6N3oyALM/dN\nha2lLVYOWgeFhULskoiIjAZvPyOjphN0mLJ3InJLc/FJ/8/RzrW92CURERkVjsjJqK3KWI4D1/bh\n6ZZD8eqTr4tdDhGR0WGQk9E6qf4NHx2aD6WtOxY/FctbzYiIHoBBTkapuLwYk3aNg1anRUzACijt\nlGKXRERklBjkZJT+k/Y+zmoyMb7LBAxsMVjscoiIjBaDnIzO7ss7sf7kGnRw64j3e/9H7HKIiIwa\ng5yMiqpIhWl7w6CQK7Bi0DrYWtqKXRIRkVFjkJPREAQBbydPhrpYhTn/mofOT3QRuyQiIqPHICej\n8dWp9Ui6nIj+Tf0xoWuY2OUQEZkEBjkZhbO3MzEvdQ5crV2xLGAl5DL+1SQiqgl+sxuJTluhxaTd\n41FcXozlA9eikUNjsUsiIjIZHPaQ6KKOLMBJdQZe6TgGz7YZJnY5REQmhUFOojp4fT+Wn1iKVs6t\n8WHfKLHLISIyOQxyEk1uiQZTdk+AXCbHikFr4WDlIHZJREQmh0FOohAEAe+kvIWswut4t+dseHv0\nFLskIiKTxCAnUXyb+Q22XfgBvRr+C9N7zBS7HCIik8Ugp3r3552LmH3gXTgqnLBi0FpYyC3ELomI\nyGTx9jOqV+W6ckze/SYKywqwfOAaNHdqIXZJREQmjSNyqlefH/8Ux7KP4N9tX8SI9i+JXQ4Rkclj\nkFO9OXrzMKKPfYymDs3wyYDPIZPJxC6JiMjkMcipXlzNv4JJu8ZDEATEDlwNZ2sXsUsiIjILegV5\nWVkZZs6ciZCQEIwePRpXr169b507d+5g3LhxmDZtWpXlR44cQe/evZGcnFy5LDQ0FC+++CJCQ0MR\nGhqK33//XZ+yyEhl5JzA0C0DcSX/Mt7tORt+TfqKXRIRkdnQ68Nu27dvh5OTE6Kjo3Hw4EFER0dj\nyZIlVdaJjIyEt7c3zpw5U7nsypUr+PLLL9GjR4/79rlo0SK0b99en3LIiCVd+hlvJr2G4vJiLOgT\nhTf5VDMiIoPSa0SelpaGwMBAAICfnx/S09PvW2fBggXw9vauskypVCI2NhaOjo76HJZMzBe/r8WY\nn0MgQMCXQzYxxImI6oBeI3K1Wg03NzcAgFwuh0wmg1arhUKhqFzHweH+r9u0tbV96D5jYmKg0WjQ\npk0bREREwMbG5qHrurrawdLS8PceK5XSe4NRFz3rBB1m7ZqFz9I+g7u9O/4X8j/0atLL4MfRF8+z\ndEixb/YsPdUGeUJCAhISEqosy8jIqPKzIAiPVcSYMWPg6emJ5s2bIzIyEps2bcK4ceMeur5GU/RY\nx3sQpdIRKlW+wfdrzOqi5+LyYkzZMwH/u7AVbV3a4ZtnvkNLRSuj+bPleZYOKfbNns3bw96wVBvk\nwcHBCA4OrrIsPDwcKpUKHTp0QFlZGQRBqDIar6170/QAEBAQgB07dui9LxKPuliNMTtG4Vj2EfRu\n3AdfDdkEVxs3scsiIjJrel0j79OnDxITEwEAycnJ8PX11bsAQRAwduxY5OXlAQAOHz6Mdu3a6b0/\nEsfF3PMI2jIQx7KP4IV2wdj83FaGOBFRPdDrGnlQUBBSU1MREhIChUKBqKi7z5Fes2YNevbsCS8v\nr8pwzs7ORmhoKMLCwlBaWor169fj4sWLOHXqFDZu3IgvvvgCI0eOxNixY2FrawsPDw9MnTrVoE1S\n3Tp84xBe/XkUbpfcxtve7yC81/v8shcionoiEx73ArcI6uJ6iJSus9xjiJ5/PP89puyZgHJdOT4d\nsASjO71qoOrqBs+zdEixb/Zs3vS+Rk70IIIgIPbXpfgw7QM4WDni66Hx8G8+UOyyiIgkh0FOtVau\nK8fsA+9iw6n1aGTfGJueSUDnJ7qIXRYRkSQxyKlWCsoK8ObOsdh9JQlPNuiCb55JQCOHxmKXRUQk\nWQxyqrGbhTfwyk8jcVKdAf9mA7Hu6Q1wVDiJXRYRkaTx6WdUI3/cOoWhWwbipDoDoZ3G4r9Bmxni\nRERGgCNyqlbK1WS8vjMU+do8zP3XPEzt/jZvLyMiMhIMcnqkuNP/xcyUaZBDjlWB6/FCu+DqNyIi\nonrDIKcHEgQBHx9diMXHPoGLtQu+HhqPfzX2E7ssIiL6BwY53UdbocXbyVOQcDYezZ1aIv6ZLWjr\nyq/NJSIyRgxyqiK3RIPXEkfjl6wD8PbwwddDv4XSTil2WURE9BAMcqp0Je8yXv5pBM5qMhHU6jms\nGLQWdlZ2YpdFRESPwNvPCADwa046hm4ZiLOaTEzoOhnrn/6aIU5EZAI4IifsvPQzJiS9huLyYnzU\n9xOM95oodklERFRDDHKJW39yNeYcnAVrC2t8NfQbDG31jNglERFRLTDIJUon6DBz50wsPrQYT9gq\nsSloM7p7eItdFhER1RKDXIKKy4sRtvsN/HRxG9q7emLTMwlo4dRS7LKIiEgPDHKJURWpMObnUTie\nfRQDWgzA2oFfw8XGVeyyiIhIT/zUuoRcyD2HoO8H4nj2UYxo/xJ2jt7JECciMnEMcok4lJWKoC2D\ncDnvEmZ4v4vlA9fA2tJa7LKIiOgxcWpdArae24IpeyZABx2W+C/Hyx1DxS6JiIgMhEFuxgRBwLIT\nS7DgUCQcrBzxxZCNeKpZgNhlERGRATHIzVS5rhyz9s/Exj++RGP7Jvjm2e/QqcGTYpdFREQGxiA3\nQwXafIxPehV7r+xG5ye88M0zCWho30jssoiIqA4wyM3MjYIsvLJjJH5X/4aBzQOxdvBXcFA4il0W\nERHVEX5q3YycUv+OoVsG4nf1bxjT6XVsDPqWIU5EZOY4IjcTyVf2YNzOMSgoy8f7vf+DKd2mQyaT\niV0WERHVMckHeU5RDoK3PY8KWRmcLF3gauMKVxs3uFq7wuVvv//7MjcbNzhYORpNUH5zeiPeSZkO\nOeRYE/glhrd7UeySiIionkg+yC1kFrCzssPVgsu4WHwR5bryGm1nKbeEi7VrlXB3eUDgu1j/9avN\n3XXtrRwM9gZAEAR8fGQBFh//FK7WrtgQFI9/NeptkH0TEZFpkHyQN7BtgJ9f3AOl0hE5OXkoKMuH\npkQDTcltaEo1yC3R4HbpbeT+c1nJbeSWanC75BYu3DkPnaCr0fGs5Fb3hbvrAwLf9a/fu1nf/dXO\n0q7KG4DSilK8tXcytpzbjBZOLRH/7Ba0cWlXV39MRERkpCQf5H8nk8ngqHCCo8IJzZ1a1Hg7naBD\ngTa/Mtw1JRpoSm9XviGoXHbvjUCpBqriHJzLPVvjNwDWFtZ/jfjvhnxuiQanb/8Bb4+e2Bj0LZ6w\nfULftomIyIQxyA1ALpPDydoZTtbOAFrVeDudoENe6Z3KUf7fw/+fI/97y7ILbyLz9hkIEPB8mxcQ\nM3AlbC1t6645IiIyagxyEcllcrjY3L2eDueab1ehq0BxeRFvLSMiIt5Hboos5BYMcSIiAsAgJyIi\nMmkMciIiIhOm1zXysrIyhIeHIysrCxYWFli0aBGaNWtWZZ07d+5gxowZsLe3R0xMDACgvLwcc+bM\nwZUrV1BRUYH33nsPPj4+OHPmDObNmwcA8PT0xPz58x+vKyIiIonQa0S+fft2ODk5IS4uDhMnTkR0\ndPR960RGRsLb27vKsh9//BG2traIi4vDwoULERUVBQBYuHAhIiIiEB8fj4KCAqSkpOhTFhERkeTo\nFeRpaWkIDAwEAPj5+SE9Pf2+dRYsWHBfkA8bNgyzZ88GALi5uSE3NxdarRbXr1+Hl5cXAMDf3x9p\naWn6lEVERCQ5ek2tq9VquLm5AQDkcjlkMhm0Wi0UCkXlOg4ODvdtZ2VlVfn7DRs24Nlnn4VGo4GT\nk1Pl8gYNGkClUulTFhERkeRUG+QJCQlISEiosiwjI6PKz4Ig1OqgmzZtwqlTp7Bq1Srcvn271vty\ndbWDpaVFrY5ZE0ql9G7pYs/SIMWeAWn2zZ6lp9ogDw4ORnBwcJVl4eHhUKlU6NChA8rKyiAIQpXR\n+KMkJCRg7969WLFiBaysrCqn2O/Jzs6Gu7v7I/eh0RTV6Fi1oVQ6QqXKN/h+jRl7lgYp9gxIs2/2\nbN4e9oZFr2vkffr0QWJiIgAgOTkZvr6+Ndru6tWriI+PR2xsLKytrQHcnW5v3bo1jh07BgBISkpC\nv3799CmLiIhIcvS6Rh4UFITU1FSEhIRAoVBUfvp8zZo16NmzJ7y8vDB27Fjk5eUhOzsboaGhCAsL\nQ1paGnJzc/Hmm29W7mv9+vWIiIjABx98AJ1Oh65du8LPz88w3REREZk5mVDbC9xGoC6mUaQ0PXMP\ne5YGKfYMSLNv9mzeHja1bpJBTkRERHfxK1qJiIhMGIOciIjIhDHIiYiITBiDnIiIyIQxyImIiEwY\ng5yIiMiE6fWFMKZE32enP2w7U3h2ek163rZtGzZs2AC5XI6RI0ciODgYRUVFCA8Ph1qthq2tLaKi\noqBUKhEaGoqioiLY2dkBAGbNmoXOnTuL0dpDGbpncz7P2dnZiIiIgFarhU6nw+zZs9G5c2cEBASg\nYcOGsLC4+xyDzz77DB4eHmK09kiG7js1NRWLFy+GhYUF+vfvj8mTJ4vU2cPp2/PKlSuRmpoKANDp\ndFCr1di5c6dJnGtD92wK51lvgpn7/vvvhXnz5gmCIAgHDhwQpk+fft8606dPF5YvXy5MnTq12u1G\njx4tZGRkCIIgCDNmzBD27dtX1y3UWnU9FxYWCoMHDxby8vKE4uJi4ZlnnhE0Go3w5ZdfCp988okg\nCIJw9OhRYe7cuYIg3O05MzOzfpuopbro2VzPc1RUlBAXFycIgiAcP35ceP311wVBEAR/f3+hoKCg\nfpvQg6H7Hjp0qJCVlSVUVFQIISEhwrlz5+q3oRrQt+d/7mPt2rWCIJjGuTZ0z6ZwnvVl9lPr+j47\n/UHbmcqz06vrOSMjA126dIGjoyNsbGzQo0cPpKen49KlS5W9+fj44Pjx4/Veu74M2bO5n2dXV9fK\nBxXl5eXB1dW13mt/HIbs++rVq3B2dkajRo0gl8sxYMAAszrX95SXlyMuLg6jR4+u17ofhyF7NpXz\nrC+zn1rX99npD9pOrVabxLPTq+v5768DgJubG1QqFdq3b4+UlBQ8/fTTOHLkCLKysirXiYmJgUaj\nQZs2bRAREQEbG5v6baoahuxZo9GY9XkeO3YsRowYga1bt6KgoABxcXGV60RGRuL69evw9vbGzJkz\nIZPJ6repGjBk3yqV6r51r169Wr8N1YC+Pd+TlJSEvn37Vvl3a+zn2pA9m8p51pdZBXldPDv9Udvp\nuy9DMkTP914fMWIEMjMzERISgl69elX+xR8zZgw8PT3RvHlzREZGYtOmTRg3bpwBu6id+ui5Nvuq\nD4bsed26dRg6dCgmTZqE5ORkfPzxx4iNjcW0adPQr18/ODs7Y/Lkydi5cyeGDBli2EZqqa77fv31\n1w1bsAEYsud7tmzZUuVzHsZ2ruujZ3NmVkFuyGenu7u737edUqms9bPT65o+Pbu7u0OtVlf+nJOT\ng27dukGhUFT+xS8sLMSePXsAoHJ6CwACAgKwY8eOumypWnXds5ubm1mf5127duGtt94CcPeRxPf6\nHz58eOW6/fv3x9mzZ0UP8rru+5/rmtu5BoCioiLcvHkTTZs2rXzd2M51XfdsjOfZkMz+Grm+z05/\n0Ham8uz06nru2rUrTp48iby8PBQWFiI9PR0+Pj5ISUnBkiVLANz9NGi/fv0gCELlI2kB4PDhw2jX\nrl39NlQDhuzZ3M9zixYtKkc7v/32G1q0aIH8/HyMGzcOWq0WAHD06FGjPM+AYftu2rQpCgoKcO3a\nNZSXlyM5ORl9+vSp956qo2/PAHDmzBm0bt26cl1TOdeG7NlUzrO+zP7pZxUVFZg7dy4uXbpU+ez0\nRo0aPfTZ6e3atUNYWBh69er1wO3Onz9f5dnps2fPFrvF+1TXc/fu3ZGYmIj169dDJpNh9OjRGDZs\nGEpKSjBt2jTk5ubC2dkZixcvhqOjI3bs2IF169bB1tYWHh4eWLhwIWxtbcVuswpD92zO5zknJwdz\n5sxBSUkJAGDOnDno0KEDNmzYgK1bt8La2hqdOnXC+++/b3TXTQHD93306FF89tlnAIDBgweLetno\nYfTtGUDlrVd/n2Y2hXNt6J5N4Tzry+yDnIiIyJyZ/dQ6ERGROWOQExERmTAGORERkQljkBMREZkw\nBjkREZEJY5ATERGZMAY5ERGRCWOQExERmbD/A+AzzkkTp2wLAAAAAElFTkSuQmCC\n",
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- }
- }
- ]
- },
- {
- "metadata": {
- "id": "jrsUps0nu8vj",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "** Question **
\n",
- "Why did I created a session to plot the graph?
\n",
- "Ans) For visualizing characteristic (or tendency) of data"
- ]
- },
- {
- "metadata": {
- "id": "P3-iuxE4sjAf",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Let's define the placeholders\n",
- "\n",
- "# Placeholders?\n",
- "# The input to the model changes on iteration\n",
- "# So we cannot have a constant in the input as we did before\n",
- "# And thus we need placeholders which we can change on each \n",
- "# iteration of the training\n",
- "\n",
- "x = tf.placeholder(tf.float32, name='x')\n",
- "y = tf.placeholder(tf.float32, name='y')"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "8hPRkaoxvRyV",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Let's define the linear regression model\n",
- "\n",
- "# tf.Variable?\n",
- "# We define the model parameters as tf.Variables\n",
- "# as they get updated throghout the training.\n",
- "# And variables denotes something which changes overtime.\n",
- "\n",
- "W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
- "b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
- "\n",
- "pred_y = (W*x) + b"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "cSw1P8bkv96r",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Let's define the loss function\n",
- "# We are going to use the mean squared loss\n",
- "loss = tf.reduce_mean(tf.square(y - pred_y))"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "5G4uQqjsygNj",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# Let's define the optimizer\n",
- "# And specify the which value (i.e. loss) it has to minimize\n",
- "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "ttI7ZT-ozAm1",
- "colab_type": "code",
- "outputId": "a147d429-a076-44a1-f1cc-b48cba3461e9",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 431
- }
- },
- "cell_type": "code",
- "source": [
- "# So the graph is now built\n",
- "# Now let's execute the graph using session\n",
- "# i.e. lets train the model\n",
- "\n",
- "# What it is to train a model?\n",
- "# To update the paramters in the graph (i.e. tf.Variables)\n",
- "# So that the loss is minimized\n",
- "\n",
- "# Okay let's start!\n",
- "with tf.Session() as sess:\n",
- " # We need to initialize the variables in our graph\n",
- " sess.run(tf.global_variables_initializer())\n",
- " \n",
- " for epoch in range(n_epochs):\n",
- " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
- " \n",
- " if epoch % interval == 0:\n",
- " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
- " \n",
- " print ('Now testing the model in the test set')\n",
- " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
- " \n",
- " \n",
- " print ('The final loss is: ', final_loss)\n",
- " \n",
- " # Plotting the final predictions against the true predictions\n",
- " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
- " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
- " plt.legend()\n",
- " plt.show()"
- ],
- "execution_count": 33,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Loss after epoch 0 is 0.06481158\n",
- "Loss after epoch 20 is 0.06480222\n",
- "Loss after epoch 40 is 0.06479287\n",
- "Now testing the model in the test set\n",
- "The final loss is: 0.33398113\n"
- ],
- "name": "stdout"
- },
- {
- "output_type": "display_data",
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3Xl4VOXd//H3ZCYLSSbLJDOBhH0N\nBEHCUpECggSxdrHWR6EitmK1ilqtPEpxwS7gUvSpS2uR0tYqapSm/dlqAdduIDtIwh6EsITs+z6T\n8/sjMBCyEpKcZPi8rosrc+bc55z7m+PMx7Pk3BbDMAxERESk0/mZ3QEREZFLlUJYRETEJAphERER\nkyiERURETKIQFhERMYlCWERExCS2zt5gTk5JZ2+ynsjIYAoKyk3tQ0fz9RpVX/fm6/WB79eo+i6c\n02lv9P1L7kjYZrOa3YUO5+s1qr7uzdfrA9+vUfW1n0suhEVERLoKhbCIiIhJFMIiIiImUQiLiIiY\nRCEsIiJiEoWwiIiISRTCIiIiJun0h3V0RS+99H/s37+X/Pw8KisriY2NIywsnGXLftku67/xxm/g\ncsXg53f2/3lefvnVi17vf/7zT77ylSspLi5i1aoVPPzwoxe9ThER6TytCuEDBw5wzz338L3vfY+5\nc+fWm7dhwwaef/55rFYrU6ZMYcGCBR3S0Y50330PAvDBB3/j8OF07r33gXbfxvLlLxIcHNyu63z7\n7dUkJo4nKipaASwi0g21GMLl5eX8/Oc/Z+LEiY3O/8UvfsGqVauIiYlh7ty5XHPNNQwePLjdO2qG\n7du38vbbb1BeXs699z7IQw/dy/vvfwzAY489zA033ER8/HCWLfspJSUleDweHnjgfxk8eEir1n/d\ndVc3WN+OHdsoKyslI+MoJ04c5/77H2LixEmsXfs+a9YkY7FYmD37FmpqatizJ5WFC+9n0aLH+elP\nH2PVqtfZvn0rf/jDCgzDgtPp4ic/eYKPPlrHF1/spLCwgIyMo3z3u7fy9a9f32G/NxERaZ0WQzgg\nIICVK1eycuXKBvOOHTtGeHg4vXr1AmDq1Kls3LjxokL4yQ2P8bf0v7Z5+cZ8Y9D1PHnlL9q0bHr6\nId56K4WAgIBG57/zzlt85StX8o1vXM+XXx7mhReW86tf/eZiukt2dhbLl7/I559v4P/9vz8zevTl\n/PGPv+O1196iurqGpUuX8PTTz/O73/2W5ctfpKio0Lvs8uVP8ac/vYbNFsrzzz/Dhx+uxWKxkJ5+\niN/+9vccP36MJUsWK4RFRBqxJy+NrOwMrnLOwmKxdPj2Wgxhm82GzdZ4s5ycHBwOh3fa4XBw7Nix\nZtcXGRnc7HM5g3sE4OfXvoUH9wio9/Dsph6kbbcHERx8tm1ERDAjRgwnLi4KAIvF4p0XGOhPREQw\n+/enkZ+fz6efrgegqqqiwfqtVj9+8pMHsVrr6o6MjOTFF19sdH0hIYFMnPgVnE47w4YNoKqqgqKi\nbIYMGUzv3k4AVq1a6V1vdHQoVmsNNpsf/v4ebDar93+KrrpqMlu2bGHEiBGMHz+Wnj0jsNv9qago\na/J30F109/63RPV1f75eo6/Vt/PUTn7+r5+TsjcFCxYyH8rEFRrT4dvt9BuzWhqZ4uExT/DwmCfa\nfbtnRm9yOu1NjuRUUlJJeXm1d35hYTmGYfFOG4bhfV1WVuGdf999DzFy5KgG2zrD46nlqaf+r941\n4ZyckkbXV1ZWhb9/D3JySigoKKO62k1RUSWVldWNrjc3t5SiojLc7lry8spwuz3e9eflFVNZ6aak\npJLq6lpyckooLy/H46k1fTSri9HcPvQFqq/78/Uafam+ndnbeX7rs6w98gEAia6xPDVzGX4VweRU\ntF+NHTKKksvlIjc31zudlZWFy+W6mFV2aRaLhcrKSiorKzlwYD8AI0aM5F//+gyAL788zNtvv3FR\n62tMv379ycg4Snl5OVVVVTzwwD0YhoHF4ofH4/G2CwsLw2KxcPLkSQB27txOfPzwNlQqIuLbtmVt\n4bt/v5GZa65i7ZEPGN/zKyR//S/84zufMHPQzE7rx0UdCffu3ZvS0lKOHz9Oz549+fTTT1m+fHl7\n9a3Luf76G7nzztvo338gw4bVhduNN97M0qVPcs89d1BbW8sDDyy8qPU1pkePHsyf/0MeeOAeAG6+\n+btYLBbGjEnknnvm8+ijT3rbPvzwYzz00EPU1kJcXG+uvnom69f/o20Fi4j4gEp3JVnlp8gsy+Rk\n6XHe3reaz459AsAVva5k4fhFTI6b2inXgM9nMQzDaK5BamoqzzzzDCdOnMBmsxETE8P06dPp3bs3\nSUlJbNmyxRu8M2fOZP78+c1u0OxTGL50GqUpvl6j6uvefL0+8P0au1p9hmFwrCSD1NzdpOXt5kTJ\ncU6VZ5JZmklWeSb5lfkNlvlq3BQWjlvElXFfbTCvI+pr6nR0i0fCI0eO5PXXX29y/vjx40lOTm57\nz0RERFqp2lPN/oJ9pOXuJjX3C1Jzd5Oau5vi6qIGbcMCwukZ0pOE6FH0DO5Jr5BYeob05HJXIuN6\nTjCh9w3piVkiItLpDMOgtKaEwqpCCisL6n5WFVBQWUBBZT4FVad/nvM6//S0xzh7L4wFC4MiBjO9\n79WMjB7FyOjL6B82AFdIT0L9Q02ssHUUwiIi0qGqPdWsO/IP3tn/JocKD3pD99wwbY6fxY+IwAgi\ngxwMDB9EvGMEI6MvY2T0ZQyPSiDEP6SDK+g4CmEREekQBwsOsHrvn3hn/5vkVtT9JU10DydRPaIZ\nGDGYyMBIwgMjiAiMICIosu5nYCSOIAcRQZFEBjlwBDoICwzHz+Kb4w0phEVEpN2U1ZTxt/S/snrv\nn9iUuREAR5CDu0Yv4Jbh84h36M8mz6UQFhGRNjEMg8yykxwqPMihwoPsztnFe+l/paS6GAsWruoz\nnbnDb+OaAV8j0Bpodne7JIUwkJl5knnzZjNsWDwA1dXV3HLLbUydOu2C1/XnPydTWFjIlClX8a9/\nfcb8+Xc12u7MMIT+/v4trvPw4UM8//yzDYY/nDr1K1x22WjvdFRUFD/96VMX3OfzffrpR0ybNoOD\nB/c3W4OIXDpOlBxn06mNHCw4wInKo6Sd2kt64SHK3WX12sWGxHHnqLuZEz+XvmH9TOpt96EQPq1v\n337ekCsuLuL737+FK66YSGBgUJvWN2TIMIYMGdbk/DPDELYmhJsSGhraLuMSn++NN15j2rQZLdYg\nIr6r2lPNpsyNfJzxIZ9kfMi+/L315vew9WBg+GAGRwxhUORgBoUPZkjkUC6LHo3Vr+nxAaQ+hXAj\nwsLCiYqKJi8vjz/8YSU2mz/FxYX87GdP8+yzSzl58gRut5s77vghY8eOZ+vWzbz44nM4HFFERUUT\nGxvH9u1bSUl5h1/84tlmhyF84YVXeO+9v/DRR2uxWPyYPPkq5syZS3Z2Fo8/vgh/f38GDx7a6r5n\nZp7krrt+wooVrwEwf/6t/OIXz/D7379KdLST/fv3kpV1iiee+AXDhsWzevVrfPbZx1gsfvzwh/ey\nb98eDh06wOLF/8uNN97sreHjjz8kOXk1VquVYcOG88ADC1m1akWjwy6KSPd0vOQYH2d8yMcZH/Lv\n4/+krKYUgCBrEFf3TWJqn2nEO0bwlUFjCKzy3ZulOlOXC+GQJx8j8G/tO5Rh1Teup+zJ1g9lmJl5\nkuLiIlyuuhE0wsLCeOSRR1m79n2ioqL5yU+eoLCwkB/96Ie89trbrFjxMo8//nOGDBnKwoX3Exsb\n511XeXlZs8MQ5uRk89lnH/Ob36wC4O675zNt2gxSUpK5+uqZ3HTTHN54448cOnTgon8P1dXVPP/8\ny/z1r2tYu/Z9goOD+eyzj1mx4o+cPHmCN974I4sWPc7q1a+xbNkv2b596+kaynn11V/zhz+8SXBw\nMA8//KB33vnDLiqERbq+WqOWo8VHSMtNZU9eKmmn/2UUH/G2GRg+iKv7zuXqfklMjP0qPWw9vPOc\n4V3riVndWZcLYbNkZBzl3nvvBOrGUH7ssZ96h3AcMSIBgNTUL9i1awdffLETgKqqKmpqasjMzGTI\nkLqj1csvT6Sqqsq73iNHvqRv3/4EBgYRGBjE008/X2+7e/emcfz4Me67r+66a3l5GadOneTIkS+Z\nNm0GAGPGjOPzzzc06HNpaam3zwCDBg1m9uy5TdY4evQYAJzOGPbsSePAgf2MGDESPz8/evfuw6JF\njze63LFjGfTu3dc7CtSYMWM5cGAfAKNGXQ7UDeZRWlra5LZFpHPVeGrIqcjmVFkmp8pOkVl2kv35\ne0nLS2Vv3h5Ka+qHaHSPaJL6XcP0vjOY3jeJAeEDTer5paXLhXDZk7+4oKPW9nLuNeHz2Wz+3p/z\n5t1OUtKsevP9/M6ekjn/Udx+flYMo7bJ7dps/kycOImHH3603vurV7+G5fSpnqaWb+ya8KlTmfWm\n3W639/WZ8YzP9NNq9aO2ttlHhwNgsdSvy+2uITAwsNF1ikjHK6ku5mTpSU6WniCz7OzPM4F7qiyT\n3IocDBp+Jq0WK4MjhpAQPZIRUZcxMnokCVGX4QqOMWUAg0tdlwvhrmzEiJH85z//JClpFgUF+bzz\nzlvcddcCoqOdZGQcoU+ffuzYsY2EhMu8y5w7DKHVauWRRx7k//7v195hCIcNG84rr7xEZWUlgYGB\nvPDCc9x997307duPffv2EB8/3HvqtzWCg0PIy8vDMAzy8/M4efJ4k22HDRvOH/+4CrfbTXFxEb/8\n5VM89dTyBsHcp08/jh/PoLy8jODgEHbs2M5tt81n69ZNF/5LFJFWMQyDk6Un2Jq1ma1ZW9iXt+d0\n4J5scBR7rmBbMD1DejEkcig9Q3oSE9yLmJCexATHMDhiCMMcwwmyte2GU2l/CuELMH36DLZv38IP\nf3g7Ho+H22+vOxV855338Nhjj9CzZy/vdeQzWhqG8KWXXuWmm+awYMEP8PPzY8qUqwgMDOJ//mcO\njz++iH/961MGDRrS6j6GhYVx5ZVXcscd8xg8eEizdzf36hXLNdd8jXvvvRPDMLjrrgUADB06jB/8\nYB53332/t4YFC37EQw/dh8Xix6hRlzN69OUKYZF2VOGu4IucXWw9tZltWVvYmrWZU2X1z2w5ghz0\nC+tPbGgsvULiiA2NJTY0jl4hsXX/QnsR6m/XEW030uJQhu3N7Iv5XW0Iro7g6zWqvu7N1+uD1tVY\nVlPGpsyN/PfEv9lw8t98kbOLmtoa73xXcAzjYiYwrucExsWM5zLn6C7zjGRf34ddaihDERG5eBXu\nCrac2sR/T/yL/5z4Nzuyt+Gurbtnw+ZnY1T0aMb1nMDYmPGM6zmB3qF9dER7CVAIi4i0kWEYfFmU\nzv6C/RRXFVFSXUxJdQkeWxVZRXmUVBdTWl1CXmUuu3O+oLq2GqgbFehy5xgmxU1hUtxXmdBrYrcY\ndk/an0JYRKSVssuz2Zm9je1ZW9mevY2d2dsprCpscTk/ix8jo0cxKXYyX42bzBWxV2IPCOuEHktX\npxAWEWlEUVUhX+TsYlfOTnZmb2dH9jaOlWTUazMgfCDT+yYxMnoUjiAH9gA7of52+sb0xF1mxR5g\nxx5gJ8Q/VE+XkkYphEXkkldSXewN3F3Z29mVs5PDRen12kT3iGZmv1mMiRnLGNdYLneNwREU1ej6\nfP3GJWk/CmERuaRUe6rZk5fKtqytbM/ayo7sbRwqPFivTURgBFN6T+Ny5xhGuy5ntHMMfex9daOU\ntDuFsIj4tIzio2zL2sL2rK1sy9rK7txdVHnOPlrWHhDG5LipjHaN4XLnGEY5L6dfWH8FrnQKhbCI\n+JQaTw2bTm1k/ZG1fHh0LemFh7zzrBYrI6JGkhgzjrEx40h0jWNw5BBdrxXTKIRFpNvLr8zj46Mf\n8uHRtXyS8THF1UUABNtCmDXgOq7odSWJMeMYFT2aYP9gk3srcpZCWES6nBpPDf89+W/+8eXfySw9\nicXihwULFosFv9Ov/SwWLFg4cfr5yrWnBzrpY+/L/wy7maR+s5gUN5lAa6DJ1Yg0TSEsIl1ClaeK\nfx77hL8ffo+1X77fqr+/hbq/wR0XM4GZ/Wcxs/+1DIuM1/Vc6TYUwiLSrjy1Hvbl72Vb1hbSCw8R\nGhBKRGAE4YERRAZG0r8yDqM8gIigSIKsgfzz+Ge8f/j/sf7IOu/oQL1CYrlx6M1cN/CbjIy+DMMw\nMDCo9f6sxcDAMGoJ8Q/Rgy+k21IIi8hFySo7xbasrd47kHdkb6fcXXbB6+kb1p95Cd/n6wO/SWLM\nON0sJZcEhbCIXLBd2Tt4fc9rfJLxIcdLj3nft2BhmCOesTHjSYwZR7xjOJXuSgqrCimsKqCwqpBq\nvzJOFmRTVFVISXUxl7vG8PWB32Jk9CidRpZLjkJYRFqltLqElINreH3PH9mVswOAqKAorul/LYmu\ncYztOZ4xrsQWTw3raVIiZymERaRZu7J38Kc9fyTl4LuU1ZTiZ/FjVv+vMS/h+0zrMwOrn9XsLop0\nWwphEfEyDINTZZkcLDzAnrxU/nzgXe9Rb1xobxZcfj+3DJ9Hr9BYk3sq4htaFcLLli1j165dWCwW\nFi9ezKhRo7zzPvroI1555RUCAgK47rrrmDt3bod1VkRaxzAMSmtKcNe6cdd6qDU8uGvdeAwPbsNN\nbW0tFZ4KjhQd5mDBAQ4VHuRQwQEOFh6krKbUu54zR723jvge0/sm6ahXpJ21GMKbN2/m6NGjJCcn\nk56ezuLFi0lOTgagtraWn//85/zlL38hIiKCH/zgB8yYMYOePXt2eMdF5Kzcilx2Zm9jR/Z2dmRt\nY2fOdnIrci9oHYHWQAaGD2ZI5FAGRwxmUMQQJsVNJjY0roN6LSIthvDGjRuZMWMGAIMGDaKoqIjS\n0lJCQ0MpKCggLCwMh8MBwBVXXMGGDRu44YYbOrbXIpew3Ipc9ualece53Zm9nYySo/Xa9LH35eq+\nSQRYA7H52bBa/LBabFj9rNgsNqx+Nvz9bPQLG8CQyCEMjhhKH3tfHemKdLIWQzg3N5eEhATvtMPh\nICcnh9DQUBwOB2VlZRw5coS4uDg2bdrEhAkTml1fZGQwNpu5H3Sn027q9juDr9d4KdRXVl1GWk4a\nqdmp7M7aze7sun/ZZdn12kb1iOLawdcyPnY8E+ImMD5uPK4Ql0k9bx1f33/g+zWqvvZxwTdmGYbh\nfW2xWHj66adZvHgxdrud3r17t7h8QUH5hW6yXV0Kfx7h6zX6an0ZxUfZcPI/7Mzfwmdf/pMviw5j\nYNRr08fel5n9ZjE8KoGEqJGMiRlLX3u/+n9fWw455V339+Or++9cvl6j6mvbOhvTYgi7XC5yc89e\nW8rOzsbpdHqnJ0yYwJtvvgnAc889R1ycrh+JtMQwDL4sSmfDyf+y4eR/+PzkhnoPvbAHhHFl7FcZ\nHjWCeMeI0z+H6/GMIj6mxRCeNGkSL730ErNnzyYtLQ2Xy0VoaKh3/h133MEzzzxDjx49+PTTT/n+\n97/foR0W6Y6Kq4rYmbODHVl1N09ty9pCVvkp73xHkIOvDfgGV8ZO4msJM+nlN0DXZ0UuAS2GcGJi\nIgkJCcyePRuLxcKSJUtISUnBbreTlJTETTfdxO23347FYuHOO+/03qQlcqmqcFewJy+VHVnb2J69\njZ3Z2zlUeLBem5jgnnxr0A1MjJvElbFfZWjkMO+zkn39VJ+InNWqa8ILFy6sNx0fH+99PXPmTGbO\nnNm+vRLpBjy1Ho4Wf8mevD3szU9j7+mfXxYd9o5tC3WnlifHTWWMayxjYsYyxpVIr5BYPSdZRPTE\nLJHWqHBXkJa7m105O9mds4u0vFQOFOyjwl1Rr114YAQTel5BQvTIutB1jWVQxGCNCCQijVIIi5yn\nrKaMtNxUvsjZwa6cnXyRs4sDBfvwGB5vmwC/AIZEDmN41AiGRyUwwlH3U0e4InIhFMJyySquKuJA\nwX4OFhzgQMF+DhTs40DBfjKKj9b706BgWzCJMeMY7bycUaf/DYkYir/V38Tei4gvUAiLzzMMg5Ol\nJ9ievZXtWdvYnfsFBwr2caoss0Hb6B5OJsZO4rLoUVzmHM1o5xgGRwzRncoi0iEUwuJziqoKvc9Q\n3pFdd4dydnlWvTZxob25qs90hkXGMyRyGEMd8QyNHIojKMqkXovIpUghLN3W+aeTDxbsZ3/BPo4W\nH6nXLjYkjusGfpMxrrEkxoxltPNyPfRCRLoEhbB0GVWeKvbkplJcXUy5u5yymlLKasooqymj/PTP\nkuoSTlQcJS17TxOnk6OZHDeVxJhx3tDtGdLLhGpERFqmEBZTHS85xscZH/Lx0fX86/hnlLtb92zx\nBqeTI4cxJHIYUT10OllEug+FsHSqGk8NW05t4qOM9Xx8dD178/d45w2JGMrk3lNxBrsI8Q8hxD+U\nYFswIf6hp6dDCPYP4fL+w6ksNrEIEZF2ohCWduGudbP11GaOlWRQXF1EcVUxRdVFlFQXU1RVdPq9\nIg4WHqSkui5Bg6xBzOg7k6v7zeTqvkn0Dx/Qqm3ZA+1Uosc6ikj3pxCWNiuqKuSTjI9Yd+QffJLx\nIYVVhc22D/ALIM7em5uGzWZG35lcGTeZHrYendRbEZGuRyEsAJwoOc6unJ2E+IcQHhhOWGA44QER\nhAWE1XsoxeGidNYf+Qfrj6zl88wNuGvdQN012m8PuZGR0aMIDwjHHhBWt56AcOyBYYQHhBNkCzKr\nPBGRLkkhfAnLrcjlvfS/8JeDa9iUubHJdsG2YMICw7FarJwoPe59P9E1lpn9r2Vm/2tJiBqpxzWK\niFwghfAlpriqiA++/DspB9/l38f/icfwYMHCpNjJTOt7NTW1NXXXcKuKKK6uu65bfPqabnlNObMG\nXMc1/a5lRv9riAmOMbscEZFuTSHs48pqytifv5c9eWl8dHQ9H2esp8pTBdQdyV4/5Dt8a9AN9AqN\nNbmnIiKXHoWwj3DXujlcmM7e/DSO7j7E1uM72JuX1mAwgnjHcL49+EauH/IdBoQPNLHHIiKiEO7C\nPLUejhQfZl/+PtILD1JQWUBRVSGFVYUNfpZUF9cLW4CooCgmxU1m+Olh9sbGjGd41AiTqhERkfMp\nhLsAwzA4VpLBvvw97Mvfx778PezP38fBgv1UeiqbXC7YFkJEYARxob2JCIqgf9gAhkeNYOLA8fS0\n9sfVw6WbpUREujCFsIlOlWWSvO9N3tz3Ol8WHa43L8gaxFBHPMMi44mPGsGQiKFE94gmIjCS8MAI\nwgPDCbAGNLpep9NOTo4eZiEi0tUphDtZjaeG9UfX8ubeP/FxxofUGrX0sPXg6wO/xWXRoxjmGE58\n1HD62ftrDFsRER+nEO4kB/L3s3rvn3j3wNvkVuQAMMaVyJz4W7lhyI2EBYab3EMREelsCuF2VmvU\ncqwkg/35e9mXv5e9eXvYk5fG3vw0ABxBDu4cdTffHT6PEVEJJvdWRETMpBBuhWpPNaU1JZRUl1Ba\nXUpJTQml1cXe14VVhaQXHPTeWFXuLqu3fA9bD6b3ncF342/lmgFfI9AaaFIlIiLSlSiEz1PpriQt\nbzfbs7ayPWsbO7K3cbgovVXL+vv5MzhiKMOjhjMscjjxUSOIdwynr72fru+KiEgDl3QIG4bB4aJD\nbD21hR3Z29ietZW0vFRqamu8bcICwpkYO4nIQAehAaHYA+zY/cMIDQglNMBOqH8oYQHhDAwfxIDw\ngfUGOxAREWnOJRXCle5K/pOxi3V7P2HrqU1sObWJvMo87/wAvwAuix7FmJixjHGNZWzMOAaED8LP\n4mdir0VExFf5dAhnlp5kW9ZWNp/6nC2nNvFFzs56R7l97H2Z2mc643tOINE1jhHRI3W9VkREOo3P\nhHBZTRlf5OxkW9ZWtmdtZVvWFjLLTnrn2/xsXBY9iikDJnNZeCLje35FgxaIiIipunUIF1YW8OyW\nZXyeuZG9eWl4DI93nis4hlkDrmOsaxzje36Fy12JBPsH62lSIiLSZXTrEE7N283vdq8gyBpEYsw4\nxsaMZ2zMOBJjxtE7tI+emywiIl1atw7hSbGT2XHrHpzBriafoywiItJVtSqEly1bxq5du7BYLCxe\nvJhRo0Z5561evZr33nsPPz8/Ro4cyaOPPtphnT2fxWIhzt6707YnIiLSnlr825vNmzdz9OhRkpOT\nWbp0KUuXLvXOKy0tZdWqVaxevZq33nqL9PR0du7c2aEdFhER8RUthvDGjRuZMWMGAIMGDaKoqIjS\n0lIA/P398ff3p7y8HLfbTUVFBeHhGohARESkNVo8HZ2bm0tCwtmBBhwOBzk5OYSGhhIYGMiCBQuY\nMWMGgYGBXHfddQwYMKDZ9UVGBmOzmfsIR6fTbur2O4Ov16j6ujdfrw98v0bV1z4u+MYswzC8r0tL\nS1mxYgVr164lNDSU2267jX379hEfH9/k8gUF5W3raTu5FP5EyddrVH3dm6/XB75fo+pr2zob0+Lp\naJfLRW5urnc6Ozsbp9MJQHp6On369MHhcBAQEMC4ceNITU1tpy6LiIj4thZDeNKkSaxbtw6AtLQ0\nXC4XoaGhAMTFxZGenk5lZSUAqamp9O/fv+N6KyIi4kNaPB2dmJhIQkICs2fPxmKxsGTJElJSUrDb\n7SQlJTF//nzmzZuH1WplzJgxjBs3rjP6LSIi0u1ZjHMv8nYCs68j+Pq1DPD9GlVf9+br9YHv16j6\n2rbOxmiMPhEREZMohEVEREyiEBYRETGJQlhERMQkCmERERGTKIRFRERMohAWERExiUJYRETEJAph\nERERkyiERURETKIQFhERMYlCWERExCQKYREREZMohEVEREyiEBYRETGJQlhERMQkCmERERGTKIRF\nRERMohAWERExiUJYRETEJAphERERkyiERURETKIQFhERMYlCWERExCQKYREREZMohEVEREyiEBYR\nETGJQlhERMQkCmERERGTKIRFRERMohAWERExia01jZYtW8auXbuwWCwsXryYUaNGAZCVlcXChQu9\n7Y4dO8ZDDz3EN77xjY7prYiIiA9pMYQ3b97M0aNHSU5OJj09ncWLF5OcnAxATEwMr7/+OgBut5tb\nb72V6dOnd2yPRUREfESLp6OAA3qfAAAXeklEQVQ3btzIjBkzABg0aBBFRUWUlpY2aPeXv/yFa665\nhpCQkPbvpYiIiA9qMYRzc3OJjIz0TjscDnJychq0e/fdd7nxxhvbt3ciIiI+rFXXhM9lGEaD93bs\n2MHAgQMJDQ1tcfnIyGBsNuuFbrZdOZ12U7ffGXy9RtXXvfl6feD7Naq+9tFiCLtcLnJzc73T2dnZ\nOJ3Oem0+++wzJk6c2KoNFhSUX2AX25fTaScnp8TUPnQ0X69R9XVvvl4f+H6Nqq9t62xMi6ejJ02a\nxLp16wBIS0vD5XI1OOLdvXs38fHx7dBNERGRS0eLR8KJiYkkJCQwe/ZsLBYLS5YsISUlBbvdTlJS\nEgA5OTlERUV1eGdFRER8SauuCZ/7t8BAg6Pev/3tb+3XIxERkUuEnpglIiJiEoWwiIiISRTCIiIi\nJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiY\nRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIS\nhbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkU\nwiIiIiaxtabRsmXL2LVrFxaLhcWLFzNq1CjvvMzMTH784x9TU1PDiBEj+NnPftZhnRUREfElLR4J\nb968maNHj5KcnMzSpUtZunRpvflPP/00t99+O2vWrMFqtXLy5MkO66yIiIgvaTGEN27cyIwZMwAY\nNGgQRUVFlJaWAlBbW8u2bduYPn06AEuWLCE2NrYDuysiIuI7Wgzh3NxcIiMjvdMOh4OcnBwA8vPz\nCQkJ4amnnmLOnDk899xzHddTERERH9Oqa8LnMgyj3uusrCzmzZtHXFwcd955J5999hlXXXVVk8tH\nRgZjs1nb1Nn24nTaTd1+Z/D1GlVf9+br9YHv16j62keLIexyucjNzfVOZ2dn43Q6AYiMjCQ2Npa+\nffsCMHHiRA4ePNhsCBcUlF9kly+O02knJ6fE1D50NF+vUfV1b75eH/h+jaqvbetsTIunoydNmsS6\ndesASEtLw+VyERoaCoDNZqNPnz4cOXLEO3/AgAHt1GURERHf1uKRcGJiIgkJCcyePRuLxcKSJUtI\nSUnBbreTlJTE4sWLWbRoEYZhMHToUO9NWiIiItK8Vl0TXrhwYb3p+Ph47+t+/frx1ltvtW+vRERE\nLgF6YpaIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiI\niEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIi\nJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiY\nRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImMTWmkbLli1j165dWCwWFi9ezKhRo7zzpk+fTs+ePbFa\nrQAsX76cmJiYjumtiIiID2kxhDdv3szRo0dJTk4mPT2dxYsXk5ycXK/NypUrCQkJ6bBOioiI+KIW\nT0dv3LiRGTNmADBo0CCKioooLS3t8I6JiIj4uhZDODc3l8jISO+0w+EgJyenXpslS5YwZ84cli9f\njmEY7d9LERERH9Sqa8LnOj9k77//fiZPnkx4eDgLFixg3bp1zJo1q8nlIyODsdmsF97TduR02k3d\nfmfw9RpVX/fm6/WB79eo+tpHiyHscrnIzc31TmdnZ+N0Or3T119/vff1lClTOHDgQLMhXFBQ3ta+\ntgun005OTompfehovl6j6uvefL0+8P0aVV/b1tmYFk9HT5o0iXXr1gGQlpaGy+UiNDQUgJKSEubP\nn091dTUAW7ZsYciQIe3VZxEREZ/W4pFwYmIiCQkJzJ49G4vFwpIlS0hJScFut5OUlMSUKVO4+eab\nCQwMZMSIEc0eBYuIiMhZFqOT76Qy+xSGr59GAd+vUfV1b75eH/h+jaqvbetsjJ6YJSIiYhKFsIiI\niEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIi\nJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiY\nRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIS\nhbCIiIhJFMIiIiImaVUIL1u2jJtvvpnZs2fzxRdfNNrmueee49Zbb23XzomIiPiyFkN48+bNHD16\nlOTkZJYuXcrSpUsbtDl06BBbtmzpkA6KiIj4qhZDeOPGjcyYMQOAQYMGUVRURGlpab02Tz/9NA8+\n+GDH9FBERMRHtRjCubm5REZGeqcdDgc5OTne6ZSUFCZMmEBcXFzH9FBERMRH2S50AcMwvK8LCwtJ\nSUnhD3/4A1lZWa1aPjIyGJvNeqGbbVdOp93U7XcGX69R9XVvvl4f+H6Nqq99tBjCLpeL3Nxc73R2\ndjZOpxOAzz//nPz8fG655Raqq6vJyMhg2bJlLF68uMn1FRSUt0O3287ptJOTU2JqHzqar9eo+ro3\nX68PfL9G1de2dTamxdPRkyZNYt26dQCkpaXhcrkIDQ0FYNasWXzwwQe88847vPzyyyQkJDQbwCIi\nInJWi0fCiYmJJCQkMHv2bCwWC0uWLCElJQW73U5SUlJn9FFERMQnteqa8MKFC+tNx8fHN2jTu3dv\nXn/99fbplYiIyCVAT8wSERExiUJYRETEJAphERERkyiERURETKIQFhERMYlCWERExCQKYREREZMo\nhEVEREyiEBYRETGJQlhERMQkCmERERGTKIRFRERMohAWERExiUJYRETEJAphERERkyiERURETKIQ\nFhERMYlCWERExCQKYREREZPYzO6AiIh0Y4YBtbXgdoPbjcXjPv3aU/fa4znnfU/DNrWe85Y9Pe1x\nY/Gcee3BcroNHnfda09t/XV53FjOWda7zJntn3nf7alb7+nlGrSp9UBcLPx6FQQGdvivTyEsItIW\nhuH98m4QIFVF+GUXnX7//DbNh8+5wdVk+Jx53Uj41G3P03iblsLH7TknrM5r41227me0t+8es/dE\nuzGsVrDZoKgQS3UVhkJYRLqc2trzjm7OOeo5/0u7kfAhLBD/3OJmw6fhsmcD5GywnBdQrQgfi9vd\nsE2j4XNOWJ0TPmfrcGOprW321xTVSbujPRg2W134+Fkx/P3BZsWwnn7PaoWgIGrPvLb54xcUgBtL\nXXvb2XaG1Qr+/mC11b1v9Tv72rt+G1jPrMuGYbPWTdtsddu0Wuu2b7Odfd92Tnvr2fb1+umdZz27\nrvPbWK1nt+Fvq7csfn5gsQDgdNoxcko65XevEBZpjTOn3FoIn8ZPuZ35Ij/naOX8MDg3fHrYCCoo\nrRc+DdZ1ToA0GiznnoprdHtnttn0us8eqZ3XxjAu+tcZ0Q675GIZfn51X8ZWK4atLnjqfXlbrRgB\nAd4A8Laxnpk+ExKnw8fm7w2VoOAgKt3G2TZWv7pws54XJmfCw+9MePk1DJV6AWNrGFCn32sxfPzq\ngqd+m9Phc4GcTjuFnRRSvk4hLM27yPDBU3veNZtmwqeRI59GAyLAj5DSio4Ln0Zqsbjdnfprt3fg\nug0/v7NfzOcEi/doxeaPERTkDRbDZmt1+OB35uim8fAxbDZCwoIpq/LUtTkTDNZGjmhs579/fpuz\n4dNUcDUZPlZrm8KntYKcdkoUUtIKCuGmnHu9p14YtCZ8WrjZwBsSjVzvOT98zr/ec86yDW42OHNq\nzQ/CyysbtvHUNnm9p6laOjt8Wiu4DcvU+2JvLHz8/TF69Gg0fM5dFqvVGyznnnJrPnys9dv4nTkd\ndt77VithDjvFZdXNh4/Vr8ERTYMjq8ZOuVmt3lNuZglx2ilXQIkA3TyELVlZhC59EktR0enrOo3c\nbHB++Bi1OKqqW74hoZvfbBBwzusWw+f0KbeLDp8zweINogsLn/p9bPp6T6QznPziqsbbNBU+51zv\n6fKcdqoUUiKXhG4dwtYvDxP47ttNBqbRyJc6/v51QdDIzQbe8LmYmw1sjYSP95SdtcnwuaibDc6E\nz+lrWtE9I8kpqOh+4dNaTjsehZSI+IBuHcLuKyaSdzADampafbOB02kn39e/wENCoLz5OzdFRMR8\n3TqEAYzQjryFRUREpOPosZUiIiImUQiLiIiYpFWno5ctW8auXbuwWCwsXryYUaNGeee98847rFmz\nBj8/P+Lj41myZAkWX7sRSEREpAO0eCS8efNmjh49SnJyMkuXLmXp0qXeeRUVFbz//vusXr2at99+\nm8OHD7Njx44O7bCIiIivaDGEN27cyIwZMwAYNGgQRUVFlJaWAtCjRw9ee+01/P39qaiooLS0FKfT\n2bE9FhER8REthnBubi6RkZHeaYfDQU5OTr02r776KklJScyaNYs+ffq0fy9FRER80AX/iZLRyMPb\n77zzTubNm8cPfvADxo4dy9ixY5tcPjIyGJvNeqGbbVdOp+//WZOv16j6ujdfrw98v0bV1z5aDGGX\ny0Vubq53Ojs723vKubCwkIMHDzJ+/HiCgoKYMmUK27dvbzaECwrK26Hbbed02snx8Yd1+HqNqq97\n8/X6wPdrVH1tW2djWjwdPWnSJNatWwdAWloaLpeL0NBQANxuN4sWLaKsrAyA3bt3M2DAgPbqs4iI\niE9r8Ug4MTGRhIQEZs+ejcViYcmSJaSkpGC320lKSmLBggXMmzcPm83GsGHDuPrqqzuj3yIiIt1e\nq64JL1y4sN50fHy89/UNN9zADTfc0L69EhERuQRYjMbutBIREZEOp8dWioiImEQhLCIiYhKFsIiI\niEkUwiIiIiZRCIuIiJhEISwiImKSC352dFfU3HjHq1ev5r333sPPz4+RI0fy6KOP4na7efTRR8nI\nyMDj8fDwww8zbtw4br31VsrLywkODgbgkUceYeTIkWaV5XWh9aWkpPDCCy/Qt29fAK688kruvvtu\n9u3bx5NPPgnAsGHD+OlPf2pGOY260BpfeeUVNmzYAEBtbS25ubmsW7eO6dOn07NnT6zWuueTL1++\nnJiYGFNqOldz9X300Ue88sorBAQEcN111zF37twml8nMzOThhx/G4/HgdDr55S9/SUBAgFllebWl\nvmeffZZt27bhdru56667mDlzJosWLSItLY2IiAgA5s+fz1VXXWVGSfVcaH2bNm3iRz/6EUOGDAFg\n6NChPP744112/8GF1/juu+/y3nvvedukpqayY8eOLvs9euDAAe655x6+973vef8bPGPDhg08//zz\nWK1WpkyZwoIFC4BO+gwa3dymTZuMO++80zAMwzh06JBx0003eeeVlJQY06ZNM2pqagzDMIzvf//7\nxo4dO4w1a9YYS5YsMQzDMA4cOGB85zvfMQzDMObOnWvs37+/cwtoQVvq+/Of/2w8/fTTDdY1d+5c\nY9euXYZhGMaPf/xj47PPPuuEClrWlhrPlZKSYqxcudIwDMOYNm2aUVpa2kk9b53m6vN4PMaUKVOM\nvLw8w+PxGLfffruRmZnZ5DKLFi0yPvjgA8MwDOO5554zVq9e3cnVNNSW+jZu3GjccccdhmEYRn5+\nvjF16lTDMAzjkUceMT755JNOr6E5banv888/N+67774G6+qK+88w2lbj+cs/+eSThmF0ze/RsrIy\nY+7cucZjjz1mvP766w3mX3vttcbJkycNj8djzJkzxzh48GCnfQa7/eno5sY79vf3x9/fn/Lyctxu\nNxUVFYSHh/PNb36Tn/zkJ0Dd0IyFhYWm9b8lbamvMdXV1Zw4ccL7f7fTpk1j48aNnVNECy6mRrfb\nzVtvvdXg/2y7kubqKygoICwsDIfDgZ+fH1dccQUbNmxocplNmzZ5Hw3bVfZhW+obP348L7zwAgBh\nYWFUVFTg8XhMq6E5bamvKV1x/8HF1/jrX/+ae+65p9P73VoBAQGsXLkSl8vVYN6xY8cIDw+nV69e\n+Pn5MXXqVDZu3Nhpn8FuH8LNjXccGBjIggULmDFjBtOmTWP06NEMGDAAf39/AgMDAXjttdf4+te/\n7l3+xRdf5JZbbuGJJ56gsrKyc4tpRFvqA9i8eTPz58/ntttuY8+ePd4P0hlRUVENxoU2S1trBFi/\nfj1f/epXCQoK8r63ZMkS5syZw/LlyxsderOzNVefw+GgrKyMI0eOUFNTw6ZNm8jNzW1ymYqKCu+p\nr66yD9tSn9Vq9Z6uXLNmDVOmTPFeQnjjjTeYN28eDz74IPn5+Z1f0HnaUh/AoUOH+OEPf8icOXP4\n73//C9Al9x+0vUaAL774gl69enlH14Ou9z1qs9nqfUecKycnB4fD4Z0+U3tnfQZ94prwuc790i0t\nLWXFihWsXbuW0NBQbrvtNvbt2+d99vXq1atJS0vjt7/9LQDz5s1j2LBh9O3blyVLlrB69Wrmz59v\nSh1NaU19o0ePxuFwcNVVV7Fjxw4eeeQRfve73zW5nq7mQvbhn//853rXtu+//34mT55MeHg4CxYs\nYN26dcyaNavTa2jOufVZLBaefvppFi9ejN1up3fv3i0u09x7XcGF1PfRRx+xZs0afv/73wPwrW99\ni4iICIYPH86rr77Kyy+/zBNPPNGp/W9Ja+rr378/9957L9deey3Hjh1j3rx5rF+/vsn1dDUXsg/X\nrFnDt7/9be90d/gebYuO+gx2+yPh5sY7Tk9Pp0+fPjgcDgICAhg3bhypqakAvPvuu3zyySf85je/\nwd/fH4CkpCTvzUzTp0/nwIEDnVxNQ22pb9CgQd6bWcaMGUN+fj6RkZH1TrtnZWU1emrGDG3dh+Xl\n5Zw6darel8L1119PVFQUNpuNKVOmdPl9CDBhwgTefPNNVqxYgd1uJy4ursllgoODvUcWXWUftqU+\ngH//+9/89re/ZeXKldjtdWOtTpw4keHDhwPd4zMIjdcXExPD1772NSwWC3379iU6OpqsrKwuuf+g\n7fsQ6k6xjxkzxjvdFb9Hm3N+7Wf2S2d9Brt9CDc33nFcXBzp6eneX1hqair9+/fn2LFjvP3227z8\n8sve09KGYfC9732P4uJioO4/rDN3NpqpLfWtXLmSv//970DdHYFnAmzgwIFs3boVqDuNO3nyZBMq\naqgtNQLs27ePgQMHetdTUlLC/Pnzqa6uBmDLli1dfh8C3HHHHeTl5VFeXs6nn37KxIkTm1zmyiuv\n9L7fVfZhW+orKSnh2WefZcWKFd47oQHuu+8+jh07BnSPzyA0Xt97773HqlWrgLrTnXl5ecTExHTJ\n/QdtqxHqQigkJMR7erarfo82p3fv3pSWlnL8+HHcbjeffvopkyZN6rTPoE+MorR8+XK2bt3qHe94\nz5493vGO3377bVJSUrBarYwZM4aHH36Y559/nvfff5/Y2FjvOlatWsVHH33E7373O3r06EFMTAxL\nly6lR48eJlZW50LrO3XqFP/7v/+LYRi43W7vrfWHDh3iiSeeoLa2ltGjR3tvTusKLrRGgHXr1rFh\nw4Z6p6Nfe+01/vrXvxIYGMiIESN4/PHHsVgsZpXl1Vx969ev59e//jUWi4Xbb7+db37zm40uEx8f\nT3Z2No888ghVVVXExsby1FNPec/kmOlC60tOTuall16qd33/mWeeISMjg1/+8pf06NGD4OBgnnrq\nKaKiokysrM6F1ldaWsrChQspLi6mpqaGe++9l6lTp3bZ/Qdt+280NTWVX/3qV/Uud33wwQdd7ns0\nNTWVZ555hhMnTmCz2YiJiWH69On07t2bpKQktmzZwvLlywGYOXOm9/R5Z3wGfSKERUREuqNufzpa\nRESku1IIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJ/j8hchJ6/FtY\nRwAAAABJRU5ErkJggg==\n",
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- }
- }
- ]
- },
- {
- "metadata": {
- "id": "jgmH3wwt1src",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "Okay, so we are doing good!
\n",
- "\n",
- "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
- "\n",
- "Or better, do it yourself!"
- ]
- },
- {
- "metadata": {
- "id": "OZ5TY7B_4E_v",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n",
- " # YOUR CODE HERE\n",
- " with tf.Session() as sess:\n",
- " sess.run(tf.global_variables_initializer())\n",
- " \n",
- " for epoch in range(n_epochs):\n",
- " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
- "\n",
- " if epoch % interval == 0:\n",
- " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
- "\n",
- " print ('Now testing the model in the test set')\n",
- " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
- " \n",
- " print ('The final loss is: ', final_loss)\n",
- " \n",
- " return final_preds, final_loss"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "A6MaclhK4rc6",
- "colab_type": "code",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 218
- },
- "outputId": "3bb819ff-24c9-4ece-9e8a-377471bba55d"
- },
- "cell_type": "code",
- "source": [
- "# Okay! Now let's tweak!\n",
- "_ = linear_regression(learning_rate=0.000034, n_epochs=500)"
- ],
- "execution_count": 35,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Loss after epoch 0 is 0.06481158\n",
- "Loss after epoch 50 is 0.0647882\n",
- "Loss after epoch 100 is 0.06476484\n",
- "Loss after epoch 150 is 0.064741485\n",
- "Loss after epoch 200 is 0.064718165\n",
- "Loss after epoch 250 is 0.06469486\n",
- "Loss after epoch 300 is 0.064671576\n",
- "Loss after epoch 350 is 0.06464831\n",
- "Loss after epoch 400 is 0.06462506\n",
- "Loss after epoch 450 is 0.064601846\n",
- "Now testing the model in the test set\n",
- "The final loss is: 0.3325342\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "peoHmV2M40uU",
- "colab_type": "code",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 386
- },
- "outputId": "46114ad0-17f2-4cac-ca12-d98c689b5230"
- },
- "cell_type": "code",
- "source": [
- "_ = linear_regression(learning_rate=0.0000006, n_epochs=1000)"
- ],
- "execution_count": 36,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Loss after epoch 0 is 0.06481158\n",
- "Loss after epoch 50 is 0.0647882\n",
- "Loss after epoch 100 is 0.06476484\n",
- "Loss after epoch 150 is 0.064741485\n",
- "Loss after epoch 200 is 0.064718165\n",
- "Loss after epoch 250 is 0.06469486\n",
- "Loss after epoch 300 is 0.064671576\n",
- "Loss after epoch 350 is 0.06464831\n",
- "Loss after epoch 400 is 0.06462506\n",
- "Loss after epoch 450 is 0.064601846\n",
- "Loss after epoch 500 is 0.0645787\n",
- "Loss after epoch 550 is 0.06455557\n",
- "Loss after epoch 600 is 0.064532466\n",
- "Loss after epoch 650 is 0.06450938\n",
- "Loss after epoch 700 is 0.064486355\n",
- "Loss after epoch 750 is 0.06446349\n",
- "Loss after epoch 800 is 0.06444063\n",
- "Loss after epoch 850 is 0.0644178\n",
- "Loss after epoch 900 is 0.06439498\n",
- "Loss after epoch 950 is 0.06437224\n",
- "Now testing the model in the test set\n",
- "The final loss is: 0.3309085\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "KjY_KnlE5ClG",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "## Drive the loss to a minimum."
- ]
- },
- {
- "metadata": {
- "id": "JKiHjGN15HPX",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "# YOUR CODE HERE"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "hc3syMCfF72T",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- "W = tf.Variable(np.random.random_sample(), name='weight_2')\n",
- "b = tf.Variable(np.random.random_sample(), name='bias_2')\n",
- "\n",
- "pred_y = (W*x) + b\n",
- "\n",
- "lambd = 0.01\n",
- "L2_regularization = lambd * tf.tensordot(W, W, 0)\n",
- "loss = tf.reduce_mean(tf.square(y - pred_y) + L2_regularization)\n",
- "optimizer = tf.train.AdamOptimizer(learning_rate=0.0000003).minimize(loss)"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "metadata": {
- "id": "FL4NT2CoIQAp",
- "colab_type": "code",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 386
- },
- "outputId": "8ab4fb03-3cda-46ef-d749-ce41742e2d4d"
- },
- "cell_type": "code",
- "source": [
- "final_preds, final_loss = linear_regression(n_epochs=1000)"
- ],
- "execution_count": 39,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Loss after epoch 0 is 0.01542704\n",
- "Loss after epoch 50 is 0.015424165\n",
- "Loss after epoch 100 is 0.01542129\n",
- "Loss after epoch 150 is 0.015418426\n",
- "Loss after epoch 200 is 0.015415577\n",
- "Loss after epoch 250 is 0.015412727\n",
- "Loss after epoch 300 is 0.015409879\n",
- "Loss after epoch 350 is 0.015407033\n",
- "Loss after epoch 400 is 0.015404186\n",
- "Loss after epoch 450 is 0.015401339\n",
- "Loss after epoch 500 is 0.015398496\n",
- "Loss after epoch 550 is 0.015395651\n",
- "Loss after epoch 600 is 0.015392808\n",
- "Loss after epoch 650 is 0.015389967\n",
- "Loss after epoch 700 is 0.015387124\n",
- "Loss after epoch 750 is 0.015384283\n",
- "Loss after epoch 800 is 0.015381445\n",
- "Loss after epoch 850 is 0.015378606\n",
- "Loss after epoch 900 is 0.015375769\n",
- "Loss after epoch 950 is 0.01537293\n",
- "Now testing the model in the test set\n",
- "The final loss is: 0.05965931\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "metadata": {
- "id": "DLXJjQnYIg6z",
- "colab_type": "text"
- },
- "cell_type": "markdown",
- "source": [
- "You can see after adding relularization, loss becomes very small and my model doesn't overfit (because, traning loss and test loss are much similar) "
- ]
- },
- {
- "metadata": {
- "id": "ij_jrW_PIVvQ",
- "colab_type": "code",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 347
- },
- "outputId": "98372027-bba5-44ac-e047-425437eb883a"
- },
- "cell_type": "code",
- "source": [
- "plt.plot(test_X, test_Y, 'g', label='True Function')\n",
- "plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
- "plt.legend()\n",
- "plt.show()"
- ],
- "execution_count": 40,
- "outputs": [
- {
- "output_type": "display_data",
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3Xl4VOXd//H3mZkkEBIgE5JAAmEJ\na8JiQgABFcQAClqtRYytohXr40JX91iLrYLYiq3axz7Wxz7tr26pFltEBUXBpSBLEgKEPUAIBJLJ\nQiAJWWbm/P4IThgFApJkJpPP67q4YDjnzHy/jPLh3Oec+zZM0zQRERERv2HxdQEiIiLiTeEsIiLi\nZxTOIiIifkbhLCIi4mcUziIiIn5G4SwiIuJnbL4u4CsOx3Gffn5ERCgVFTU+raE1BXp/EPg9qr/2\nLdD7g8DvsaX7i4oKP+M2nTmfZLNZfV1Cqwr0/iDwe1R/7Vug9weB32Nb9qdwFhER8TMKZxERET+j\ncBYREfEzCmcRERE/o3AWERHxMwpnERERP6NwFhER8TN+MwmJP3rhhd+zc+d2ysvLqK2tJTY2jq5d\nu7Fw4e9a5P1nzbqG6OgYLJamfyP98Y9/vuD3/eKLTxk3bgLHjlXyyisv8eCDj17we4qISNs5p3De\ntWsX99xzD7fddhs333yz17Y1a9bw7LPPYrVaueyyy7j33nsBWLhwIbm5uRiGQUZGBiNHjmz56lvZ\nj3/8cwDef/9d9u7NZ968n7X4ZzzzzPOEhoa26Hu++eZrpKSMITKyh4JZRKQdajaca2pqeOKJJxg/\nfvxptz/55JO88sorxMTEcPPNNzN9+nTKy8spKCggMzOT/Px8MjIyyMzMbPHifSU7eyNvvvkqNTU1\nzJv3c+67bx7vvfcxAL/85YNcf/1shg4dxsKFv+b48eO4XC5+9rMHGDhw0Dm9/8yZV3zj/XJysqiu\nruLAgQIOHTrIT35yH+PHT2T58vd4++1MDMMgPf0HNDQ0sG3bVu6//yc8/PBj/PrXv+SVV/7OunXr\n+O1vn8FmsxEVFc0jj/yKlStXsHnzJo4ereDAgQK+//1buPrq61rtz01ERM5Ns+EcHBzMyy+/zMsv\nv/yNbYWFhXTr1o1evXoBMGnSJNauXUt5eTlpaWkAJCQkUFlZSVVVFWFhYd+60MfX/JJ38//1rY8/\nnWsSruPxCU9+q2Pz8/fwxhtLCA4OPu32f/zjDcaNm8A111zHvn17ee65Z/jDH168kHIpKSnmmWee\n58sv1/Dvf/+TUaMu4q9//V/+9rc3qK9vYMGC+Sxa9Cz/+7//wzPPPE9l5VHPsfPnz+eZZ14gJqYn\nzz77NB99tBzDMMjP38P//M9fOHiwkPnzMxTOIiKn8WnhKhKcfehtG9gmn9dsONtsNmy20+/mcDiw\n2+2e13a7ncLCQioqKkhKSvL6fYfDcdZwjogIPeu8paGdg7FYjObKPS+hnYO9Jh4/0yTk4eGdCA1t\n2rd791ASE4cRFxcJgGEYnm0hIUF07x7Kzp15lJeXs2rVhwDU1Z34xvtbrRYeeeTnWK2NfUdERPD8\n88+f9v26dAlh/PhxREWFM2RIf+rqTlBZWcKgQQPp3TsKgFdeednzvj16hGG1NmCzWQgKcmEYBsOH\nN565T558KRs2bCAxMZExY0bTs2d3wsODOHGi+qwTsbcH7b3+5qi/9i3Q+4PA69Ftunnsk8dY+MVC\nrh58Ne/e9G6bfG6b3BBmmmaz+zS30seDyb/iweRftVRJHl+thhUVFX7GlbGOH6+lpqbes/3o0RpM\n0/C8Nk3T8+vq6hOe7T/+8X0MH950rf3r7+9yuXnqqd97XXN2OI6f9v2qq+sICuqMw3Gciopq6uud\nVFbWUltbf9r3LS2torKyGqfTTVlZtdd7lpUdo7bWyfHjtdTXu3E4jlNTU4PL5fb56mAX4mzfYSBQ\nf+1boPcHgdfjCecJfvrJ3fxrzxL6dxvA4mmLW7S/VluVKjo6mtLSUs/r4uJioqOjv/H7JSUlREVF\nXchH+TXDMKitraW2tpZdu3YCkJg4nM8+Ww3Avn17efPNVy/o/U6nb99+HDhQQE1NDXV1dfzsZ/dg\nmiaGYcHlcnn269q1K4ZhcOTIEQA2bcpm6NBh36JTEZGOwVHj4Pp/X82/9izh4l4TeP/6jxkcObjN\nPv+Cwrl3795UVVVx8OBBnE4nq1atYuLEiUycOJEVK1YAkJeXR3R09AVdb/Z31103izvvvJWFC3/N\nkCGNoTdr1o0cOlTIPffcwdNPP8lFF6Vc0PudTufOnZk79y5+9rN7+PGP/4trrrkOwzBITk7hnnvm\nel1zfuKJJ/j1rx9l3rw7cTqdXHHFtG/fsIhIANtZvoOrllxBVvEGZg2+kbe+828iO0e2aQ2G2cyY\n89atW3n66ac5dOgQNpuNmJgYpkyZQu/evZk6dSobNmzgmWeeAWDatGnMnTsXgGeeeYaNGzdiGAbz\n589n6NChZy3E10MhgTYc83WB3h8Efo/qr30L9P4gMHr8tHAVc1fM4Vh9JQ+OyeC+1IcwjMb7nVq6\nv7MNazcbzm3F119oIPxHdTaB3h8Efo/qr30L9P6g/ff46ra/8eBnP8eCheemvMj3Bs/22t6W4awZ\nwkREpMM64TzBrvIdvL0rk5c2v4i9k52/XfUm43pd7NO6FM4iIhLw3KabwuMH2FaWx7ayrWwv28a2\nsq3srczHbboBGNh9EK/NfIv+3Qb4uFqFs4iIBKjj9cf4cP9ylu1dyqeFq6hq8B6S7hbSnbE9LyYx\nMonEyOFcN/B6uoZ081G13hTOIiISMCpqy1mx/wOW5f+b1YWfUO+uB2BAtwSmRU8nMXI4w+yJJEYO\nJzYsznOzl79ROIuISLtV66zl4PFC1hR9wbv5/+I/RZ/jdDsBSIwczjUJ13L1gGsZYj/7E0P+RuF8\nFocPFzFnTjpDhjR+qfX19fzgB7cyadLl5/1e//xnJkePHuWyyybz2WermTv3v06731fLPQYFBTX7\nnnv37uHZZ3/7jWUmJ00ax4gRozyvIyMjefHFP553zV+3atVKLr88jd27d561BxGRllLnquNQ1UEK\njx2g8PgBDhwr4MDxAg4cK6Dw+AGKa4547X9RVDJXJ1zL1QO+w4DubTMPdmtQODcjPr6vJ/yOHavk\nhz/8ARdfPJ6QkE7f6v0GDRrCoEFDzrj9q+UezyWczyQsLKxF1oX+uldf/RuXX57WbA8iIufKNE12\nlG9nX+VeDlUVUni8kENVBzl0vJCDVQcpqSk+7XFWw0pceB8uibuM+PC+DItM5Kr+VxPftW8bd9A6\nFM7noWvXbkRG9qCsrIz/+7+XsdmCOHbsKL/5zSJ++9sFFBUdwul0cscddzF69Bg2blzP888vxm6P\nJDKyB7GxcWRnb2TJkn/w5JO/Petyj8899yeWLn2HlSuXYxgWLr10MjfddDMlJcU89tjDBAUFMXDg\nuU8ld/DgQe65Zx6vvPJ3AObOvYUnn3yav/zlz/ToEcXOndspLj7Cr371JEOGDOW11/7G6tUfYxgW\n7rprHjt2bGPPnl1kZDzArFk3enr4+OOPyMx8DavVypAhw/jZz+7nlVdeOu3yliIipyqpKeHBT3/O\n+/u+uZhEkCWI2LA4Lom7jNiwOPqEx9O3az/6hMcT37UvvbrEYrMEboS1m866PP5LQt5t2SUj6665\njurHz33JyMOHizh2rJLo6Bigcc7qhx56lOXL3yMysgePPPIrjh49yk9/ehd/+9ubvPTSH3nssScY\nNGgw99//E2Jj4zzvVVNTfdblHh2OElav/pgXX3wFgLvvnsvll6exZEkmV1wxjdmzb+LVV//Knj27\nLvjPob6+nmef/SP/+tfbLF/+HqGhoaxe/TEvvfRXiooO8eqrf+Xhhx/jtdf+xsKFvyM7e+PJHmr4\n85//m//7v9cJDQ3lwQd/7tn29eUtFc4icqp38//Fg5/+nLLaMsb1Gs+V/WbSJ7wPceG96R3Wh6jQ\naCzGBc0w3a61m3D2lQMHCpg3706gcW3rX/7y154lNBMTG5fF3Lp1M7m5OWzevAmAuro6GhoaOHz4\nMIMGNZ7dXnRRCnV1dZ733b9/H/Hx/QgJ6URISCcWLXrW63O3b8/j4MFCfvzjxuu6NTXVHDlSxP79\n+7j88sa1spOTU/nyyzXfqLmqqspTM0BCwkDuuefM14dHjUoGICoqhm3b8ti1ayeJicOxWCz07t2H\nhx9+7LTHFRYeoHfveM+qWsnJo9m1awcAI0deBDQujlJVVXXGzxaRjqW8toxHPrufd/b8k07WTjw5\ncRF3jLyrQwfx6bSbcK5+/MnzOsttKadec/46my3I8/OcObczdeqVXtstlqb/2L4+S6rFYsU8+eD7\nmd57/PiJPPjgo16//9prf8M4+R/xmY4/3TXn+vpjXq+dTqfn11+tJ/1VnVarBbe7+VldDcO7L6ez\ngZCQkNO+p4jIiv0fcN/qn1BSU8zomDH88Yr/IaH7IF+X5Zf0T5UWkJg4nC+++BSAiopyXnrpvwHo\n0SOKAwf2Y5omOTlZXsc0t9zjkCHDyM7Oora2FtM0+cMfnqGurpb4+L7s2LENwDOEfC7CwsKoqCjH\nNE3KykopKjp4xn2HDBnGli25OJ1OysvLeOSR+wG+Edh9+vTl4MED1NRUA5CTk82QIYnnXJOIdAyV\ndUf58cd3ccv7N3K0toLHxv+GZd/9UMF8Fu3mzNmfTZmSRnb2Bu6663ZcLhe33944pHznnffwy18+\nRM+evTzXqb9y6nKPADfe+H2v5R5feOHPzJ59E/fe+yMsFguXXTaZkJBO3HDDTTz22MN89tkqEhLO\n/T/sbt26kZo6ljvumMPAgYPOerd1r16xTJ8+g3nz7sQ0Tf7rv+4FYPDgIfzoR3O4++6feHq4996f\nct99P8YwLIwceRGjRl3Exo3rzuvPT0QCj2ma7K7YxWcHV/HHnOcoqj7EyKiLeGHK/zAsUv+Ib45W\npTqpva+m0pxA7w8Cv0f1174Fen8AdSGVvJO7jM8Pfsrnhz7lSPVhAGwWG78Y/SA/TbmPIOu3f0zU\n17QqlYiI+D3TNPns4Go+2LeMzw6uZs/R3Z5tPTr34LsDv8elvSdzeZ8riAvv7cNK2x+Fs4iInBfT\nNFlZsILFG58mu6TxfppQWxdmDJrBuKhLuKz3ZIZFJuoO7AugcBYRkXNimiYr9n/A4o1Pk+vIAWDm\ngO/woxF3kdpzLHE9IwN+6L6tKJxFROSs3KabD/a9x+KNT7O1dDMGBt9J+C6/SH2QxMgkX5cXkBTO\nIiJyWrXOWlbsf5/fZz3DtrKtGBhcP2gWPxv9AEPtw3xdXkBTOIuIiMexukpWHviQ9/a+y8cFH1Hj\nrMZiWJg1+EZ+PvoBBkWc+5z+8u0pnEVEOriSmhKW73uP9/e9y+cHP6XB3QDAgG4JzBhwDT8Ydosm\nDGljCmcRkQ6k1lnL7oqdbCvLY3v5NjYeWc+GI+swaZzyYkSPUcwccA0zBlzDkIihGIbh44o7JoWz\niEgAMk2TgmP7T4ZwHtvLtrG9LI+9lfm4TJdnPwODi2MnMKP/1QG1HnJ7p3AWEWnn6l317KrYydbS\nzWwt3cyW0s1sLd3C8a8teNM1uBupPccyzJ7IsMgkhkUmkWhPpGtINx9VLmeicBYRaWdM0yS7ZCP/\n2PkGG49sYGf5durd9Z7tBgYJ3QeSFj+VpB4jSIxMYpg9idiwOA1TtxPnFM4LFy4kNzcXwzDIyMhg\n5MiRnm0rV67kT3/6E8HBwcycOZObb76ZdevW8dOf/pRBgxpvIBg8eDCPPXb6NYFFROTcOGocvL0r\nkzd2/J0d5dsB6GTtRFKP4QzvMfLkjxEkRg6nS1AXH1crF6LZcF6/fj0FBQVkZmaSn59PRkYGmZmZ\nALjdbp544gneeecdunfvzo9+9CPS0tIAGDt2LM8//3zrVi8iEuCcbiefHPiI17e/yocFH+B0Owm2\nBHNtwvXcNOxmLus9GZtFg6CBptlvdO3atZ7ATUhIoLKykqqqqpPrA1fQtWtX7HY7ABdffDFr1qwh\nLi6udasWEQlwhccP8LetfyFz5+sU1xwBIDFyOD8YdgvfGzwbe6dIH1coranZcC4tLSUpqWl6Nrvd\njsPhICwsDLvdTnV1Nfv37ycuLo5169YxduxY4uLi2LNnD3fddReVlZXMmzePiRMntmojIiLtnWma\nbDiynpc2/zfv7V2K23TTLaQ7tw//Ed8fdgsjeozSNeMO4rzHQk5d/tkwDBYtWkRGRgbh4eH07t24\nJFi/fv2YN28eV111FYWFhcyZM4cPP/yQ4ODgM75vREQoNpv1W7TQcs62tmYgCPT+IPB7VH/t25n6\na3A18Pa2t/n9l79nQ9EGAC7qeRE/v/jnzE6aTSdbp7Ys84J01O+wpTUbztHR0ZSWlnpel5SUEBUV\n5Xk9duxYXn/9dQAWL15MXFwcMTExzJgxA4D4+Hh69OhBcXExffr0OePnVFTUfOsmWkKgL4Qe6P1B\n4Peo/tq30/VXUVvO37f9lVe2/JnD1UUYGFzV/2ruGnUvF/eagGEYHK9o4DgNPqr6/HTE7/BC3+9M\nmg3niRMn8sILL5Cenk5eXh7R0dGEhYV5tt9xxx08/fTTdO7cmVWrVvHDH/6QpUuX4nA4mDt3Lg6H\ng7KyMmJiYlqmGxGRdsDpdlJcfYSSmmKKa4o5caCS/OICimuKKTn5Y1vZVk44T9AlKIw7R97NHSPu\nol+3/r4uXfxAs+GckpJCUlIS6enpGIbB/PnzWbJkCeHh4UydOpXZs2dz++23YxgGd955J3a7nSlT\npnD//ffz8ccf09DQwOOPP37WIW0RkUBgmiabSrL5x643eGf325TXlp9x3yBLEP269ueWpNv4/tBb\nNBGIeDHMUy8i+5Cvh0I0HNP+BXqP6s9/HTxeyNu7MvnHzjfYc3Q3AD06R3Fp3GXEdOlFTGhPBvbs\nS2dXN6JDY4gOjSYixB5wN3e15+/wXPjVsLaIiHzT8fpjLMtfylu73uSLQ58BjROCXDfwemYPuYnJ\nfa7wev440INLWpbCWUTkHNW56vi44COW7H6LjwqWc8J5AoAJsZdww+B0rkm4VsPT0iIUziIiZ+F0\nO/ni0Ge8s/tt3tv7LsfqKwEY2H0QswbfyKzBN2olJ2lxCmcRka8xTZOs4g0s2f0W/97zDo4TJQDE\ndonjlsTbuH7QLIb3GBlw14zFfyicRUROKjx+gLd2vknmztfZV7kXAHsnO7cmzeV7g25gbK+LsRgW\nH1cpHYHCWUQ6tKqGKpbl/5t/7HzDc2NXZ1tnrh90A7MGz2ZS7ykEWYN8XKV0NApnEelw3KabNUVf\nkLnjdd7N/zc1zmoALu41gRuHfJ/vDLyO8OCuPq5SOjKFs4h0GG7TzXt73+W36xews2IHAPFd+zF7\n8I+ZPeQmzc4lfkPhLCIBzzRNVhasYNH6BWwpzcVqWJk1+EZuSbyNcb3G6zqy+B2Fs4gEtM8Oruap\ndU+QVbwBA4PrB93AA2MeJqH7IF+XJnJGCmcRCUjrDn/J0+uf9NzkNXPAd3hwTAbDIhN9XJlI8xTO\nItJuuNwuXt/xd/5380uccNZgMSxYDSsWw4LFsGK1NP66wdXA9vI8ANLip/HQ2EcZFZ3s4+pFzp3C\nWUTahdWFnzD/P4+yvTyPEGsI9k6RuEwXbtON++TPLtON23Rjmm4u7T2Zh8Y8ythe43xdush5UziL\niF/bWb6DX6/5JSsPfIiBwfeH3sLD435Jzy69fF2aSKtROItIm6qoLedo3VFiw+IIsYaccT9HjYPf\nbVjI37f9FZfp4tK4STw+cQEjeoxsw2pFfEPhLCKtrsHVwMoDH/Lmjtf4qGA5TrcTgOjQGHqH9SYu\nvA+DogZgt0YTF96H/KN7eC57McfrjzGw+yDmT3iSaX2v1FzW0mEonEWk1Wwry+ONHa/yz12ZlJ4o\nBSAxcjhJkcM5XF3EweOFbC3dQnZJFuR7H2vvZOepS3/HnMTbNX2mdDgKZxFpUeW1ZSzZ9RZv7nyd\nzY5NQGPQ/mjEXaQP/QEjokZ57e823ThOOKi2lrG1cCcHqw4C8P2hN9O9U0Sb1y/iDxTOItIiTNPk\nr3mv8Os1v6TGWYPVsDK931XcOOQHTOt3JcHW4NMeZzEsxITGEBU1kAEhegZZBBTOItICjlQf5mer\n7uWTAyvpHtKd+8c8wg1D0okJjfF1aSLtksJZRC7I0j3v8MCnP6OiroLJfabw3OUv0iss1tdlibRr\nCmcR+VYq647yyOcP8PauTDrbOrPossX8MOkO3VEt0gIUziJy3j4/+Ck/+eRuDlUdJDk6hf++4mUG\nRmghCZGWonAWkXN2uKqIFzc9z0ubX8RqWHlgzCP8LOV+Peok0sIUziJyRlX1x1lT9AWfFq7i04Or\n2FWxE4CE7gN58YqXSY4Z7eMKRQKTwlmkg3Obbupd9TS466l3NbCvMp9PD67i08JVbCxe75nNK9QW\nyhXxU7m8zxXcnHgboUGhPq5cJHCdUzgvXLiQ3NxcDMMgIyODkSOb5rZduXIlf/rTnwgODmbmzJnc\nfPPNzR4jIm3rSPVhlux+m3d2v82hqoOnhHE9LtN12mMMDC6KTmZS7ylM6nM5qT3HnnUubBFpOc2G\n8/r16ykoKCAzM5P8/HwyMjLIzMwEwO1288QTT/DOO+/QvXt3fvSjH5GWlsaBAwfOeIyItI2qhire\ny1/K27sy+fzQp7hNN0GWIPp27UewNYRgSxBB1mCCLcEEWYNO/hxMj85RXNZ7EpfEXUZEJ7uv2xDp\nkJoN57Vr15KWlgZAQkIClZWVVFVVERYWRkVFBV27dsVub/wf+OKLL2bNmjUUFhae8RgRaT1Ot5PP\nDq7mrZ1v8sG+ZdQ4awBIjRnLDUPSuXbgd7F3ivRxlSLSnGbDubS0lKSkJM9ru92Ow+EgLCwMu91O\ndXU1+/fvJy4ujnXr1jF27NizHiMiLaumoYbPDq7mw/0fsGL/BzhOlADQr2t/bhiSzqzBN9K/2wAf\nVyki5+O8bwgzTdPza8MwWLRoERkZGYSHh9O7d+9mjzmTiIhQbDbr+ZbToqKiwn36+a0t0PuDwO/x\nq/4OHz/Msl3LWLprKSv3rqTWWdu4PTSKe1Lv4ZZRtzAubly7mxCko3x/gSzQe2yr/poN5+joaEpL\nSz2vS0pKiIqK8rweO3Ysr7/+OgCLFy8mLi6Ourq6sx5zOhUVNeddfEuKigrH4Tju0xpaU6D3B4Hf\n43Gbgz9/+RdW7HufTY4cz+8PtQ9jWt+rmNbvKkbHpGK1NP4jt7S0ylelfiuB/v0Fen8Q+D22dH9n\nC/pmw3nixIm88MILpKenk5eXR3R0tNfw9B133MHTTz9N586dWbVqFT/84Q/p1avXWY8RkXPjNt18\nWriKV7a8xEcFKzAxsVlsXBo3ien9GgO5X7f+vi5TRFpYs+GckpJCUlIS6enpGIbB/PnzWbJkCeHh\n4UydOpXZs2dz++23YxgGd955J3a7Hbvd/o1jROTcHa8/RuaO13ll65/JP7oHgHFx47h5yA+5sv8M\nuoV093GFItKaDPNcLgi3AV8PhWg4pv0LhB53le/kL1v/TObON6huqCLYEsx1g77H3OF3Mm345Hbf\n39kEwvd3NoHeHwR+j341rC0iret4/THezf83b+18k/8UfQ5Ary6x/CT559yceBtRoWe/X0NEAo/C\nWcQHGlwNrCpcydu7Mlm+731qXY13W0+IvYS5I+7kqv5XY7Pof0+Rjkr/94u0EdM0ySnJ4u1dmfxr\nzz8pPdH4RENC94HcMDid7w2eTd+u/XxbpIj4BYWzSCtyuV1sKF7Pin3v88G+ZeytzAegR+ce3DHi\nv7hhcDoXRae0u+eRRaR1KZxFWlhVQxWrD3zCiv3vs7JgBWW1ZUDjqk7XDbyeGwanM7nPFVoDWUTO\nSOEs0gJKakp4f++7rNj/Pp8f/JR6dz0AMaE9mZN4O1f2v4pL4ibRydbJx5WKSHugcBb5lipqy3l/\n7zLe2fNPvji56hNAUuQIpve/iiv7zWBk1EVYDIuPKxWR9kbhLHIequqP88G+9/j3niWsKvyYBncD\nAKNjxnDdwOuZMeAa+oTH+7hKEWnvFM4izSg9Ucrqwo95f+8yVhas8Dz2NKLHKK4b9D2uTfgu8V37\n+rhKEQkkCmeRr3G6nWws3sCqAx+x6sDH5Do2YdI4kd6g7oP57qBZXDfwewyMGOTjSkUkUCmcRYDD\nVUV8fOAjPjmwks8OruZYfSUANouNCbGXcHl8Gml9pzHMnqjHnkSk1SmcpcOqaqjivfyl/GPXm3xx\n8FPP2XF8eF+uHzSLKfFTuSTuUsKCA3t9WhHxPwpn6VBcbhdfHPqMf+x8g/f2LqXG2biO+NieF/Od\nhOu4ou9UBnQbqLNjEfEphbMEPNM02VG+nbd3ZfL2rkwOVxcBEN+1H7MHpzNryI0M6Jbg4ypFRJoo\nnCUgHa8/xucHP+OTAytZXfgxB44XANA1uBu3JN7GDUNuYlzPi3WGLCJ+SeEsAcFtusk+nM2S3KV8\nUriSDUfW4XQ7gcZAvnrAtVw78LtM63cVnW2dfVytiMjZKZzF71XVH2dH+XbKa8sory2n9ERp469P\nlFFeW0bpiVL2H9vrWeXJwCA5OoXJ8Vcwpc9UUmJGa/lFEWlX9DeW+K3KuqO8lPsif978J8+jTadj\ns9joGdqLW0fdyoToSVzW+3IiO0e2YaUiIi1L4Sx+5+uhHNkpkv8aeQ8xXXoR2SkSe+dIr5+7BnfD\nMAyiosJxOI77unwRkQumcBa/UVl3lD9v/hMv5b7oCeVfjX+CHw6/gy5BXXxdnohIm1E4i88plEVE\nvCmcpVWZpkn+0T0UHj/AkerDHK4u4nD1YY5UF3Gk+giHq4tw1JRgYnpC+bbhcwkLCvN16SIiPqNw\nllbzZdEaFq77DV8eXnPa7Z2snejZpRcXx05gat8rFcoiIicpnKXF5Zbk8NT6J/jkwEoApsSnMabn\nOHp1iaVnl14nf+5J95AITQIiInIaCmdpMTvLd/D0+gUs2/tvACbGXkrGxb9iTM9xPq5MRKR9UTjL\nGZWeKOW5rGc4VHWIXl160TNkkhH7AAAgAElEQVQsltgusY1nvmGNZ8CdbZ0pOLaf3214ird3ZeI2\n3aREj+aRcb/ist6TdWYsIvItnFM4L1y4kNzcXAzDICMjg5EjR3q2vfbaayxduhSLxcLw4cN59NFH\nWbJkCc899xzx8fEATJgwgbvvvrt1OpAW53K7+H/b/o+n1v2Go3VHz7pv95DuVDVU4XQ7GWZP5JFx\nv2J6v6sUyiIiF6DZcF6/fj0FBQVkZmaSn59PRkYGmZmZAFRVVfHKK6/w4YcfYrPZuP3229m0aRMA\nM2bM4KGHHmrd6qXFZRVv4KHP7mOzYxNhQeE8MfEprh14PcXVRzh88m7rI9VFFFU13XXd2xrPvOSf\nct3A72ExLL5uQUSk3Ws2nNeuXUtaWhoACQkJVFZWUlVVRVhYGEFBQQQFBVFTU0NoaCgnTpygW7du\nrV60tLzSE6Us+PJxXtv+/wCYNfhG5o9/gpguPQHo2aUXo0j2ZYkiIh1Gs+FcWlpKUlKS57Xdbsfh\ncBAWFkZISAj33nsvaWlphISEMHPmTPr3709OTg7r169n7ty5OJ1OHnroIRITE8/6ORERodhs1gvv\n6AJERYX79PNb2+n6c7ldvJz9MhkfZ1BRW8Hw6OH894z/5rK+l/mgwgvXEb/DQKL+2r9A77Gt+jvv\nG8JM0/T8uqqqipdeeonly5cTFhbGrbfeyo4dOxg1ahR2u53JkyeTk5PDQw89xLvvvnvW962oqDn/\n6ltQoM/L/PX+9lXuZcX+9/nHzjfZWrrZM4R9+/A7CbIGtcs/i472HQYa9df+BXqPLd3f2YK+2XCO\njo6mtLTU87qkpISoqCgA8vPz6dOnD3a7HYDU1FS2bt3KrFmzSEhIACA5OZny8nJcLhdWq2/PjDsy\nl9vF+sPrWLH/fVbsf59dFTs92743aDaPT3jSM4QtIiK+1Ww4T5w4kRdeeIH09HTy8vKIjo4mLKxx\nFqe4uDjy8/Opra2lU6dObN26lUmTJvHyyy/Tq1cvrr76anbt2oXdblcwt7ETzhMcrjrEtrJtfFjw\nASsPrKC0pvEfWZ1tnbmy3wym9buKqX2nK5RFRPxMs+GckpJCUlIS6enpGIbB/PnzWbJkCeHh4Uyd\nOpW5c+cyZ84crFYrycnJpKam0rt3bx544AHefPNNnE4nCxYsaIteOpSv5qzeUprLoapDHKoq5FDV\nIYqqDnHoeCFltWVe+/cM68ktibcxrd9VXBo3idCgUB9VLiIizTHMUy8i+5Cvr1O0h2sl9a561hb9\nh48KlvNRwQr2Ve79xj6dbZ2JDYsjNqw3vcN607drPyb3mcLUpEmUlVb7oOq20x6+wwuh/tq3QO8P\nAr9Hv7rmLL5VXFPMxwUf8lHBClYXfkJ1QxUAXYLCmDngO0yInUjv8Hh6h/UmNqw39k72004AoueP\nRUTaD4Wzn9pWlscjn9/P2qL/eH6vf7cBTOs7h7S+0xkfO5Fga7APKxQRkdaicPYzTreTF7J/zzMb\nF9HgbmBC7CVM7zeDaf2mk9B9kK/LExGRNqBw9iPby7bxk0/uJteRQ88uvVg86Tmm9rvS12WJiEgb\nUzj7ga+fLd845Ps8MfEpuneK8HVpIiLiAwpnH9tRvp2ffHwXmxw5xIT25NnJz+tsWUSkg1M4+8jR\n2gr+mvcKz2xYRL27ntlDbuLJiYt0tiwiIgrntmKaJrsrdvFhwXI+KljO+sNf4jJdxIT2ZPHk55jW\n7ypflygiIn5C4dyK6lx1rDn0BSsLVvBhwXIKju0HwMAgJSaVaX2v5IfD79DZsoiIeFE4f0u1zloO\nHi+kpKYYx4mSxp9rHJTUFJ/8PQd7ju72TBoSFhTONQnXMbXvdK6In0ZUaJSPOxAREX+lcD4PbtPN\n2qL/8I+db7A0/1+e4D2dTtZOxHfty+XxaUzreyXjeo3XpCEiInJOFM7nYE/Fbt7a9QZv7czkYFUh\nAH3C47k24bvEdIkhOjSGqM7RRIfGEB0aTVRoNGFB4aedRlNERKQ5CuczKK8t4197lvDWzjfIKt4I\nNA5Nf3/oLcwechMXx07QfNUiItIqFM6ncJtuvjj0Ga9u+yvv711Gvbsei2FhSnwas4fcxJX9Zmqp\nRRERaXUKZ6CkpoS/fPEi/7PhJfYf2wfA4Igh3DT0Fr43+AZ6dunl4wpFRKQj6bDh7DbdrC78hFe3\n/Y3l+9/D6XbSydqJG4d8n5sTb2Nsz3G6ZiwiIj7R4cK54Nh+/rHzDTJ3vM6B4wUAJEYO556xdzE9\n9jt0C+nu4wpFRKSj6xDhXNVQxbL8f5O543X+U/Q5AKG2Lvxg2BxuSbyN5OjRREd3xeE47uNKRURE\nAjic3aabL4vW8ObO11i651/UOKsBmBB7CelDf8DVCdcSFhTm4ypFRES+KSDD+f29y/jVmgwOnJwu\nMz68L7OH/JjZQ26iX7f+vi1ORESkGQEZzp8cWElpTQk3Dvk+6UN/wPjYiXomWURE2o2ADOffTfo9\nT1+2GKvF6utSREREzltAhrNhGFgNBbOIiLRPGusVERHxMwpnERERP6NwFhER8TPndM154cKF5Obm\nYhgGGRkZjBw50rPttddeY+nSpVgsFoYPH86jjz5KQ0MDDz/8MEVFRVitVp566in69OnTak2IiIgE\nkmbPnNevX09BQQGZmZksWLCABQsWeLZVVVXxyiuv8Nprr/HGG2+Qn5/Ppk2bWLZsGV27duWNN97g\nrrvuYvHixa3ahIiISCBpNpzXrl1LWloaAAkJCVRWVlJVVQVAUFAQQUFB1NTU4HQ6OXHiBN26dWPt\n2rVMnToVgAkTJpCdnd2KLYiIiASWZoe1S0tLSUpK8ry22+04HA7CwsIICQnh3nvvJS0tjZCQEGbO\nnEn//v0pLS3FbrcDYLFYMAyD+vp6goODz/g5ERGh2Gy+ffwpKircp5/f2gK9Pwj8HtVf+xbo/UHg\n99hW/Z33c86maXp+XVVVxUsvvcTy5csJCwvj1ltvZceOHWc95kwqKmrOt5QWFRUVHtALXwR6fxD4\nPaq/9i3Q+4PA77Gl+ztb0Dc7rB0dHU1paanndUlJCVFRUQDk5+fTp08f7HY7wcHBpKamsnXrVqKj\no3E4HAA0NDRgmuZZz5pFRESkSbPhPHHiRFasWAFAXl4e0dHRhIU1ruYUFxdHfn4+tbW1AGzdupV+\n/foxceJEli9fDsCqVasYN25ca9UvIiIScJod1k5JSSEpKYn09HQMw2D+/PksWbKE8PBwpk6dyty5\nc5kzZw5Wq5Xk5GRSU1NxuVysWbOGm266ieDgYBYtWtQWvYiIiAQEwzyXC8JtwNfXKXStpP0L9B7V\nX/sW6P1B4PfoV9ecRUREpG0pnEVERPyMwllERMTPKJxFRET8jMJZRETEzyicRURE/IzCWURExM8o\nnEVERPyMwllERMTPKJxFRET8jMJZRETEzyicRURE/IzCWURExM8onEVERPyMwllERMTPKJxFRET8\njMJZRETEzyicRURE/IzCWURExM8onEVERPyMwllERMTPKJxFRET8jMJZRETEzyicRURE/IzCWURE\nxM/YzmWnhQsXkpubi2EYZGRkMHLkSACKi4u5//77PfsVFhZy33330dDQwHPPPUd8fDwAEyZM4O67\n726F8kVERAJPs+G8fv16CgoKyMzMJD8/n4yMDDIzMwGIiYnh73//OwBOp5NbbrmFKVOmsGLFCmbM\nmMFDDz3UutWLiIgEoGaHtdeuXUtaWhoACQkJVFZWUlVV9Y393nnnHaZPn06XLl1avkoREZEOpNlw\nLi0tJSIiwvPabrfjcDi+sd9bb73FrFmzPK/Xr1/P3LlzufXWW9m2bVsLlSsiIhL4zuma86lM0/zG\n7+Xk5DBgwADCwsIAGDVqFHa7ncmTJ5OTk8NDDz3Eu+++e9b3jYgIxWaznm85LSoqKtynn9/aAr0/\nCPwe1V/7Fuj9QeD32Fb9NRvO0dHRlJaWel6XlJQQFRXltc/q1asZP36853VCQgIJCQkAJCcnU15e\njsvlwmo9c/hWVNScd/EtKSoqHIfjuE9raE2B3h8Efo/qr30L9P4g8Hts6f7OFvTNDmtPnDiRFStW\nAJCXl0d0dLTnDPkrW7ZsYejQoZ7XL7/8MsuWLQNg165d2O32swaziIiINGn2zDklJYWkpCTS09Mx\nDIP58+ezZMkSwsPDmTp1KgAOh4PIyEjPMddccw0PPPAAb775Jk6nkwULFrReByIiIgHGME93EdkH\nfD0UouGY9i/Qe1R/7Vug9weB36NfDWuLiIhI21I4i4iI+BmFs4iIiJ9ROIuIiPgZhbOIiIifOe8Z\nwkRERAJeXR22rZsJyt6ILWsjttwcmPU9uO/RNvl4hbOIiHRspoll397GIM7e2Pjz1i0Y9fWeXdzd\nu8PXZsdsTQpnERHpUIyKcmw5WQRlnQzjnCws5eWe7abNhnP4CJwpqTSkpOIcnYprwECiortCGz3H\nrXAWEZHAVV+PbdtWbFkbPWfGtvw9Xru44vtRO+nypjAeMQo6dfJRwY0UziIiEhhME8uBgqbh6ayN\n2LbkYtTVeXZxh3el/rLLaRg9GmfKGBpSUjHbcLj6XCmcRUSkXTIqj2LLyT7lWnEWllKHZ7tpteJM\nHN54Rjw6FWdKKq6Bg8Di/w8qKZxFRMT/NTRg257nPTy9e5fXLq643tR+57tNw9MjR0FoqI8KvjAK\nZxER8S+mieXQQc/QdFD2RmybN2GcOOHZxd0ljPpLLvO6acsd09OHRbcshbOIiPiUUXUcW05203Xi\n7I1YS4o9202LBdfQRM/QdENKKq7BQ8Bq9WHVrUvhLCIibcfpxLpju9czxdadOzBOWb3Y1SuWupnf\n8ZwRN4y8CMLCfFh021M4i4hIq7EcLvK6Thy0KQejptqz3QztQsP4id7D071ifVixf1A4i4hIy6iq\nImjNF15hbD1c5NlsGgauIUMbQzgllYbRY3ANGQo2RdHX6U9ERETOn8uFdddOr2eK2bGN7m530y7R\nMdRdOdNzrdh5UTJmeFcfFt1+KJxFRKRZluIj3o8xbcrBUtU0laXZuTNMmEDNiGRPGLvjeoNh+LDq\n9kvhLCIi3mpqsG3O9b5p62Ch1y7OQYOpH91005ZzaCJRsXaq22ju6UCncBYR6cjcbqx7dns9xmTb\nthXD5WrapUcP6qZd2XTTVnIKZrfuPiw68CmcRUQ6EMPhOHlGvIGgrCxsm7KxHKv0bDdDQnAmj/Z6\nptgd31fD021M4SwiEqhOnMC2ZTNB2Rs8c09bDxR47eJMGEj99KuahqcTh0NwsI8Klq8onEVEAoHb\njXVvPrasDSfPjLOw5W3BcDqbdrHbqUub5j08HWH3YdFyJgpnEZF2yCgrazwj/uoO6pxsLJVHPdvN\n4GCcoy5qeqY4JRV3v/4anm4nFM4iIv6urg7b1s2NIXwyjK3793nt4uw/gPq0aU3PFCeNgJAQHxUs\nF+qcwnnhwoXk5uZiGAYZGRmMHDkSgOLiYu6//37PfoWFhdx3331ceeWVPPzwwxQVFWG1Wnnqqafo\n06dP63QgIhJITBPLvr1ejzHZtm7BqK/37OLu3p36KWlNc08nj8a0R/qwaGlpzYbz+vXrKSgoIDMz\nk/z8fDIyMsjMzAQgJiaGv//97wA4nU5uueUWpkyZwrJly+jatSuLFy/miy++YPHixfzhD39o3U5E\nRNoho6IcW06W5zGmoJwsLOXlnu1mUBDOpOGe6S6do1Nx9U/Q8HSAazac165dS1paGgAJCQlUVlZS\nVVVF2NdWCHnnnXeYPn06Xbp0Ye3atVx33XUATJgwgYyMjFYoXUSknamvx5a3xfuZ4r35Xru44vtR\nO+nyppu2RoyCTp18VLD4SrPhXFpaSlJSkue13W7H4XB8I5zfeust/vKXv3iOsdsb7wC0WCwYhkF9\nfT3Buj1fRDoK08RSsN8zPM3mHHrk5GDU1Xl2cXftRv2ky5ueKU5OxYyK8mHR4i/O+4Yw85Q1N7+S\nk5PDgAEDvhHYZzvm6yIiQrHZfLtwdlRUuE8/v7UFen8Q+D2qPz929Chs2ADr1jX9cDiatlutGCNH\nwrhxcPHFMG4clsGDCbZYCKTTlnb9HZ6Dtuqv2XCOjo6mtLTU87qkpISor/3LbvXq1YwfP97rGIfD\nwdChQ2loaMA0zWbPmisqas639hYVFRWOI4DnhA30/iDwe1R/fqShAdv2PO+FIHbv8trF1bsPDd/5\nrmd4OuKKS3BUu7zfp6yaQNKuvsNvoaX7O1vQNxvOEydO5IUXXiA9PZ28vDyio6O/cYa8ZcsWZsyY\n4XXM8uXLufTSS1m1ahXjxo27gPJFRHzINLEcLPR6jMm2JRfjxAnPLu6wcOovneQJ4oaUVMyYGO/3\nCQ2F6sANLmlZzYZzSkoKSUlJpKenYxgG8+fPZ8mSJYSHhzN16lQAHA4HkZFNt/HPmDGDNWvWcNNN\nNxEcHMyiRYtarwMRkRZkHD+GbVOO56atoKwNWBwlnu2mxYJrWFLTY0wpqbgGDQarby/LSWAxzHO5\nINwGfD0UouGY9i/Qe1R/rcDpxLpju/fSiDt3YJzy16KrVyzO0WOawnjkRdCly3l/VKB/fxD4PfrV\nsLaISKCwFB3yuk4clJuDUdN0v4sZ2oWG8RObHmManYq7V6wPK5aOSuEsIoGpqoqg3ByvMLYeOezZ\nbBoGrqHDvOaedg0dpuFp8QsKZxFp/1wurLt2nrxpawNBWRux7tyO4XY37RIdQ91VVzfNPX1RMmZY\nYD/2I+2XwllE2h1L8RHvx5hysrFUV3m2m5074xwzjobRYzxh7I6N05SX0m4onEXEv9XUELR5k/fw\n9KGDXrs4Bw+h/pTrxM6hiRAU5KOCRS6cwllE/IfbjXXP7sabtTZuaDwr3p6H4WqavMPdI4q66Vc1\n3bSVnILZtZsPixZpeQpnEfEZo6Skae7pLTlErt+A5fgxz3YzJARn8mjPakwNKam4+8RreFoCnsJZ\nRNrGiRPYNud6P1NceMBrF/fAQdRfOaNpeDpxOGjBHOmAFM4i0vLcbqz5exrvnM7eiC07C9u2rRhO\nZ9MukZHUTZ3uGZ7uPnUSFU79lSQCCmcRaQFGaSlBOafMPZ2TjaXyqGe7GRyMc1Ry09KIKam4+/bz\nHp6OCIcAnl1K5HwonEXk/NTVYdtyyvB01kasBfu9dnH2H0B92jQaUsc0PlOcNELD0yLnQeEsImdm\nmlj35Xs/U7x1C0ZDg2cXd0QE9VPSmuaeTh6NaY88y5uKSHMUziLiYVSUey+NmJOFpaLCs90MCsI5\nfITX3NOu/gm6e1qkhSmcRTqq+npseVs8Q9O2rA3Y9u312sUV34/ay69oCuPhI6FTJx8VLNJxKJxF\nOgLTxFKw3+s6sW3rZoy6Os8u7q7dqJ90+Sk3bY3B7NHDh0WLdFwKZ5EAZFQexZad1RTGOVlYSks9\n202bDWficJwpo08OT4/BlTAQLBYfVi0iX1E4i7R3DQ3Ytuc1XSfO2oBtz26vXVx94qm99vqm4emR\no6BzZx8VLCLNUTiLtCemieVgofdNW5s3YdTWenZxh4VTf+nkpuHp5NGYMTE+LFpEzpfCWcSPGceP\nYcvJJih7I2zdROTaL7E4SjzbTYsF17CkpseYUlJxDRoMVqsPqxaRC6VwFvEXTifWHdsJytrQNPf0\nrp0YpunZxYyNo+7qa5vCeORF0KWLD4sWkdagcBbxEUvRIa/rxEGbN2HU1Hi2m6FdaJhwiec6cbdp\nkykPCvdhxSLSVhTOIm2hqoqg3ByvmbasRw57NpuGgWvosMYz4pRUGkaPwTVkqPfwdJTmnhbpKBTO\nIi3N5cK6c4f33NM7t2O43U27xPSk7qqrPTdtOS9KxgzTWbGINFI4i1wgy5HD3nNPb8rBUl3l2W52\n7kzD2ItPnhE3hrE7Nk5TXorIGSmcRc5HdTVBmzd5D08XHfJsNg0D1+Ah1KU0LY3oGpYINv2vJiLn\nTn9jiJyJ2411106vZ4qtO7ZhuFxNu0RFU3flDM/zxM7kFMyu3XxYtIgEgnMK54ULF5Kbm4thGGRk\nZDBy5EjPtsOHD/OLX/yChoYGEhMT+c1vfsO6dev46U9/yqBBgwAYPHgwjz32WOt0INJCjOJigrJP\nGZ7OycZS1XQDltmpE87RY7yeKXb37qPhaRFpcc2G8/r16ykoKCAzM5P8/HwyMjLIzMz0bF+0aBG3\n3347U6dO5de//jVFRUUAjB07lueff771Khe5ECdOYNuc23TTVvZGrIUHvHZxDhpMfco1njB2DkuC\noCAfFSwiHUmz4bx27VrS0tIASEhIoLKykqqqKsLCwnC73WRlZfHss88CMH/+fAAKCwtbsWSR8+R2\nY83f0/gscfZGbNlZ2LZtxXA6m3aJjKRu6vSmuaeTUzC7R/iwaBHpyJoN59LSUpKSkjyv7XY7DoeD\nsLAwysvL6dKlC0899RR5eXmkpqZy3333AbBnzx7uuusuKisrmTdvHhMnTjzr50REhGKz+XbKwaio\nwH6UJdD7g5M9Ohywbl3Tj/XrobKyaafgYEhNhXHjPD8s/fsTYhiE+K70cxLo36H6a/8Cvce26u+8\nbwgzT51K0DQpLi5mzpw5xMXFceedd7J69WqGDRvGvHnzuOqqqygsLGTOnDl8+OGHBAcHn/F9Kypq\nzritLURFheMI4AkeAra/2lpsWxqHp8PycnGt+RLrgf1euzj7D8CZNr3xMabRY3AmjWgM6FOVVuHv\nAvY7PEn9tX+B3mNL93e2oG82nKOjoyk9ZR3YkpISoqKiAIiIiCA2Npb4+HgAxo8fz+7du5k8eTIz\nZswAID4+nh49elBcXEyfPn0uqBHp4EwT675876UR87ZiNDR4djEiIqifktZ001byaEx7pA+LFhE5\nf82G88SJE3nhhRdIT08nLy+P6OhowsLCGg+22ejTpw/79++nX79+5OXlMXPmTJYuXYrD4WDu3Lk4\nHA7KysqI0ZJ1cp6M8jKCcrKawjgnC0tFhWe7GRSEc/gIz3XirlMnU9YtRndPi0i712w4p6SkkJSU\nRHp6OoZhMH/+fJYsWUJ4eDhTp04lIyODhx9+GNM0GTx4MFOmTKGmpob777+fjz/+mIaGBh5//PGz\nDmmLUF+Pbetmz3SXtuyN2Pbt9drF1bcftZdf0XTT1vCR0KlT0w6ae1pEAoRhnnoR2Yd8fZ1C10ra\nkGli2b/P6zEm25bNGPX1nl3c3brjTE45ZXg6FbNHj7O+rV/12ArUX/sW6P1B4PfoV9ecRS6UUXkU\nW3aWVxhbyso8202bDWfSCJwpo0+G8RhcAxLAYvFh1SIivqNwlpbV0IBt21bvhSD27PbaxdUnntpL\nJnmWRnSOGAmdO/uoYBER/6Nwlm/PNLEUHvCae9q2JRejttazizu8K/WXTvasxtSQkooZHe3DokVE\n/J/CWc6ZcfwYtpxsr3WKLY4Sz3bTasU5LMlraUTXoMEanhYROU8KZzk9pxPr9m3ec0/v2olxyv2D\nrtg46q6+tvE6ceoYGkaMgi5dfFi0iEhgUDhL4/B00SGvx5iCNm/CqGmatc0M7ULDhEuaHmManYq7\nZy8fFi0iErgUzh2QUXUc26YcrzC2Fh/xbDctFlxDhnldJ3YNGQpW3859LiLSUSicA53LhXXnDti9\nlbBPvyAoayPWndsx3O6mXXr2om7GKUsjjroIMyywJ68XEfFnCucAYzly2Psxpk05WKobF3XoDJih\noTSMvdjrpi13XG/fFi0iIl4Uzu1ZdTVBuTleYWw9XOTZbBoGrsFDqEtJpfOkSygfNBzXsESw6WsX\nEfFn+lu6vXC5sO7e1fRMcdYGrDu2eQ1Pu6OiqbtyRtNNW8kpmOFdAegcFY4rgKfVExEJJApnP2UU\nFxOUfcrwdE42lqqmcDU7d8Y5ZhwNXx+e1opMIiLtnsLZH9TUYNuc6/1M8cFCr12cgwZTn3KN55li\n59BECAryUcEiItKaFM5tze3Gume399KI27ZiuFxNu/ToQd20K72Hp7t192HRIiLSlhTOrcwoLSUo\ne0NTGOdkYzlW6dluhoTgTB7t9UyxO76vhqdFRDowhXNLqq3FtuWU4emsLKwH9nvt4hyQQP20Kz1h\n7EwaAcHBvqlXRET8ksL52zJNrHv3eD9TnLcVo6HBs4s7IoK6K6Y2PVOcPBozwu7DokVEpD1QOJ8j\no7zMe2nEnCwsR496tptBQThHjGy8RvzV8HT/ARqeFhGR86ZwPp26Omx5W7xv2tq312sXV7/+1E6Z\ninP0yZu2ho+EkBAfFSwiIoFE4WyaWPbvg4/y6LL688az4i2bMerrPbu4u3WnfvIUGkaPaQzj5FTM\nyEgfFi0iIoGsw4WzcbQCW3ZW001bOVlYysoACAVMmw1n0gicKaNPLgQxBteABLBYfFu4iIh0GIEd\nzg0N2LZtbbpOnLUBW/4er11c8X2pvXQSnS67hIrBI3COGAmdO/uoYBERkQAN5+AVHxD6/LPYtuRi\n1NZ6ft8d3pX6Syd7PVNsRkcD0CkqHKfmnhYRET8QmOH80Qps2RtxDkvyWhrRNWiwhqdFRMTvBWQ4\nV/3u91Qt/K0m9xARkXbpnMJ54cKF5ObmYhgGGRkZjBw50rPt8OHD/OIXv6ChoYHExER+85vfNHtM\nqzMMBbOIiLRbzY7xrl+/noKCAjIzM1mwYAELFizw2r5o0SJuv/123n77baxWK0VFRc0eIyIiImfW\nbDivXbuWtLQ0ABISEqisrKSqqgoAt9tNVlYWU6ZMAWD+/PnExsae9RgRERE5u2bDubS0lIiICM9r\nu92Ow+EAoLy8nC5duvDUU09x0003sXjx4maPERERkbM77xvCTNP0+nVxcTFz5swhLi6OO++8k9Wr\nV5/1mDOJiAjFZrOebzktKioq3Kef39oCvT8I/B7VX/sW6P1B4PfYVv01G87R0dGUlpZ6XpeUlBAV\nFQVAREQEsbGxxMfHA7w3fJoAAAn3SURBVDB+/Hh279591mPOpKKi5ls10FKiosJxBPBzzoHeHwR+\nj+qvfQv0/iDwe2zp/s4W9M0Oa0+cOJEVK1YAkJeXR3R0NGFhYQDYbDb69OnD/v37Pdv79+9/1mNE\nRETk7Jo9c05JSSEpKYn09HQMw2D+/PksWbKE8PBwpk6dSkZGBg8//DCmaTJ48GCmTJmCxWL5xjEi\nIiJybgzzXC4ItwFfD4VoOKb9C/Qe1V/7Fuj9QeD36FfD2iIiItK2FM4iIiJ+RuEsIiLiZ/zmmrOI\niIg00pmziIiIn1E4i4iI+BmFs4iIiJ9ROP//9u40JKrvj+P4e1zTMmssp8XCjFIjEqGirDQtow0r\ngkAyK402WyhKbdN60G7RrmYGUraQSUhJilQQabYghYaZQWR7aouTls50fg/ES+aW8+c/Mw7n9eze\n8Vzm43fOOXfOvXolSZIkyczIyVmSJEmSzIycnCVJkiTJzHT6kZFdyZ49e3jy5AkqlYqtW7cyatQo\n5bX09HSysrKwsrJi5MiRbNu2DZ1Ox7Zt23j9+jV6vZ7o6GhGjx7NokWLqK2txdHREYCYmBhGjhxp\nqliKzubLzMzk6NGjylPE/Pz8WLVqFaWlpezcuRMAT09Pdu3aZYo4LXQ2X2JiIvn5+QD8/v2byspK\ncnJyCAoKol+/flhbNz6SNCEhAY1GY5JMf2svY15eHomJidjZ2TFr1izCwsLabPP+/Xuio6PR6/X0\n7duXgwcPYmdnZ6pYCkPyHThwgMePH6PT6VixYgXTpk0jNjaWkpISevXqBUBkZCSTJ082RaRmOpuv\nsLCQ9evXM2zYMACGDx/Ojh07LKZ+V65cISsrS/mZ4uJiioqKzHYMBSgrK2P16tUsWbJE+Qw2yc/P\n5/Dhw1hbW+Pv709UVBRgpD4oLFRhYaFYvny5EEKI8vJysWDBAuW1mpoaERgYKBoaGoQQQixdulQU\nFRWJjIwMER8fL4QQoqysTMyfP18IIURYWJh4/vy5cQN0wJB8V69eFfv27WtxrLCwMPHkyRMhhBAb\nN24Ud+7cMUKC9hmS70+ZmZkiJSVFCCFEYGCg0Gq1Rnrn/669jHq9Xvj7+4uqqiqh1+tFRESEeP/+\nfZttYmNjRXZ2thBCiEOHDon09HQjp2nJkHwFBQVi2bJlQgghqqurRUBAgBBCiJiYGHHr1i2jZ2iP\nIfnu378v1q5d2+JYllK/v9vv3LlTCGGeY6gQQvz48UOEhYWJ7du3i3PnzrV4fcaMGeLdu3dCr9eL\n0NBQ8eLFC6P1QYtd1i4oKGDq1KkADB06lG/fvqHVagGwtbXF1taW2tpadDoddXV1ODs7ExISwpYt\nWwBQq9V8/frVZO+/I4bka019fT1v375VzogDAwMpKCgwToh2/C/5dDodFy9ebHEWbG7ay/jlyxd6\n9uyJWq3GysqKcePGkZ+f32abwsJCpkyZAnSNGraVb8yYMRw9ehSAnj17UldXh16vN1mG9hiSry2W\nUr8/nTx5ktWrVxv9fXeGnZ0dKSkpuLq6tnitoqICZ2dn+vfvj5WVFQEBARQUFBitD1rs5FxZWUnv\n3r2VbbVazefPnwGwt7cnKiqKqVOnEhgYiI+PD0OGDMHW1hZ7e3sA0tLSmD17ttL+2LFjLFy4kLi4\nOH7+/GncMK0wJB/AgwcPiIyMZPHixTx79kzpZE1cXFyU45iSofkAcnNzmThxIt26dVP2xcfHExoa\nSkJCAsJM/ileexnVajU/fvzg1atXNDQ0UFhYSGVlZZtt6urqlCW0rlDDtvJZW1srS58ZGRn4+/sr\nlyPOnz9PeHg4GzZsoLq62viB/mJIPoDy8nJWrlxJaGgo9+7dA7CY+jV5+vQp/fv3p2/fvso+cxtD\nAWxsbJqNE3/6/PkzarVa2W7Kb6w+aNHXnP/054Cs1WpJTk7m5s2b9OjRg8WLF1NaWoqXlxfQeD2z\npKSEpKQkAMLDw/H09GTw4MHEx8eTnp5OZGSkSXK05V/y+fj4oFarmTx5MkVFRcTExHDmzJk2j2NO\nOlO/q1evNrtuvm7dOiZNmoSzszNRUVHk5OQwffp0o2foyJ8ZVSoV+/btY+vWrTg5OeHm5tZhm/b2\nmYPO5MvLyyMjI4OzZ88CMGfOHHr16oW3tzenT5/mxIkTxMXFGfX9d+Rf8rm7u7NmzRpmzJhBRUUF\n4eHh5Obmtnkcc9KZ+mVkZDBv3jxluyuMoYb6f/VBi/3m7Orq2uxM7tOnT8pZ3MuXLxk0aBBqtRo7\nOztGjx5NcXExAFeuXOHWrVucOnUKW1tbAIKDg5WbqIKCgigrKzNympYMyTd06FDlJhpfX1+qq6vp\n3bt3s+X7jx8/trrEY2yG1q+2tpYPHz40Gyzmzp2Li4sLNjY2+Pv7m0X9oP2MAGPHjuXChQskJyfj\n5OTEwIED22zj6OiofBvpCjWE1vMB3L17l6SkJFJSUnByanze7fjx4/H29ga6Rh+E1vNpNBpmzpyJ\nSqVi8ODB9OnTh48fP1pU/aBxmd7X11fZNscxtCN/52+qi7H6oMVOzhMmTCAnJweAkpISXF1d6dGj\nBwADBw7k5cuXyi+yuLgYd3d3KioquHTpEidOnFCWt4UQLFmyhO/fvwONH7qmOy1NyZB8KSkpXL9+\nHWi8Q7FpcvPw8ODRo0dA45LwpEmTTJCoOUPyAZSWluLh4aEcp6amhsjISOrr6wF4+PChWdQP2s8I\nsGzZMqqqqqitreX27duMHz++zTZ+fn7K/q5QQ2g9X01NDQcOHCA5OVm5Mxtg7dq1VFRUAF2jD0Lr\n+bKyskhNTQUal02rqqrQaDQWUz9onJi6d++uLPGa6xjaETc3N7RaLW/evEGn03H79m0mTJhgtD5o\n0U+lSkhI4NGjR6hUKuLj43n27BlOTk4EBwdz6dIlMjMzsba2xtfXl+joaA4fPsyNGzcYMGCAcozU\n1FTy8vI4c+YMDg4OaDQadu/ejYODgwmTNepsvg8fPrB582aEEOh0OuVPAMrLy4mLi+P379/4+Pgo\nN8WZWmfzAeTk5JCfn99sWTstLY1r165hb2/PiBEj2LFjByqVylSxmmkvY25uLidPnkSlUhEREUFI\nSEirbby8vPj06RMxMTH8+vWLAQMGsHfvXmXlx5Q6m+/y5cscP3682T0E+/fv5/Xr1xw8eBAHBwcc\nHR3Zu3cvLi4uJkzWqLP5tFotmzZt4vv37zQ0NLBmzRoCAgIspn7QeLJ85MiRZpfMsrOzzXIMLS4u\nZv/+/bx9+xYbGxs0Gg1BQUG4ubkRHBzMw4cPSUhIAGDatGnKUrwx+qBFT86SJEmS1BVZ7LK2JEmS\nJHVVcnKWJEmSJDMjJ2dJkiRJMjNycpYkSZIkMyMnZ0mSJEkyM3JyliRJkiQzIydnSZIkSTIzcnKW\nJEmSJDPzH653HelbT8fDAAAAAElFTkSuQmCC\n",
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- }
- }
- ]
- },
- {
- "metadata": {
- "id": "nQ0XTZi2Iv2H",
- "colab_type": "code",
- "colab": {}
- },
- "cell_type": "code",
- "source": [
- ""
- ],
- "execution_count": 0,
- "outputs": []
- }
- ]
-}
\ No newline at end of file