diff --git a/First_Date_with_TensorFlow.ipynb b/First_Date_with_TensorFlow.ipynb
new file mode 100644
index 0000000..b26d034
--- /dev/null
+++ b/First_Date_with_TensorFlow.ipynb
@@ -0,0 +1,1133 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "name": "First_Date_with_TensorFlow.ipynb",
+ "version": "0.3.2",
+ "provenance": [],
+ "include_colab_link": true
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ }
+ },
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ " "
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
\n",
+ "\n",
+ "You know what's important for understanding Deep Learning / Machine Learning?
\n",
+ "Intuition. Period.\n",
+ "\n",
+ "And Intuition comes when you run the code multiple times.\n",
+ "\n",
+ "So, today I can write a couple of defination and say this is this, this is that.
\n",
+ "You Google half of the things up. You find answers which you need to Google further.
\n",
+ "In the process, you probably won't even remember what's the first thing you started out with!\n",
+ "\n",
+ "So?\n",
+ "\n",
+ "Hence on, I will execute cells with code.
\n",
+ "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
+ "**No Theory Just Code.**\n",
+ "\n",
+ "I will at max give a defination that extends for a line. That's it.
\n",
+ "Let's get started!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "**RECOMMENDED!**
\n",
+ "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
+ "Don't just `shift+enter` the cells.\n",
+ "\n",
+ "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "gYWUpE-bYKWP",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Essential imports\n",
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "C4sGcsglnWRS",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "eKpz5NCIYMdi",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define some tensors\n",
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
+ " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "c1RIduyvnfN7",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0,2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0],[2.0, 3.0], [4.0, 5.0]],\n",
+ " [[1.0,9.0], [2.0,3.0], [4.0, 5.0]]])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "vmMcjzTxbWzw",
+ "colab_type": "code",
+ "outputId": "af6ef332-6289-4f89-ed30-4b2c5f0683f7",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 69
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's print them out!\n",
+ "print (t1)\n",
+ "print (t2)\n",
+ "print (t3)"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_1:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_2:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "10ahnfjYbcop",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Where's Waldo?
\n",
+ "I mean, the value?
\n",
+ "\n",
+ "So, the thing is you can't print the value of tensors directly.
\n",
+ "You have to use `session`, so let's do that!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ol6O5I7Tb2nb",
+ "colab_type": "code",
+ "outputId": "85c01d87-bc2a-4751-ad7b-99d0960b97aa",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 208
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "sess = tf.Session()\n",
+ "print (sess.run(t1))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t2))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t3))\n",
+ "sess.close()"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OPPEmDLIn_rE",
+ "colab_type": "code",
+ "outputId": "5de7fd75-bb31-4daf-d3cb-ba878b1fbcb8",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 194
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "s = tf.Session()\n",
+ "print(s.run(t1))\n",
+ "print(s.run(t1))\n",
+ "print(s.run(t2))\n",
+ "print(s.run(t3))"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "2.0\n",
+ "[1. 2.]\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "rXKfVs_zb-kU",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Aaahaa!! Just printed those tensors!!!
\n",
+ "Feels good!
\n",
+ "\n",
+ "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
+ "And you are still using the markdown cells for the theory ?!\n",
+ "\n",
+ "I am just gonna say I am a unreasonable man.
\n",
+ "\n",
+ "\n",
+ "So, you are programming with tf.
\n",
+ "What ever you do is broken down to 2 basic steps:\n",
+ "- Building the computational Graph!\n",
+ "- Execute that graph using `session`!\n",
+ "\n",
+ "That's all!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Let's compare this 2 steps with what we did above!
\n",
+ "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
+ "And then I executed each tensor in this graph using a `session`.\n",
+ "\n",
+ "That simple!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Now, let's define a few more computational graphs and execute them with sessions.\n",
+ "\n",
+ "Okay, to start with let's build this computational graph!\n",
+ "\n",
+ "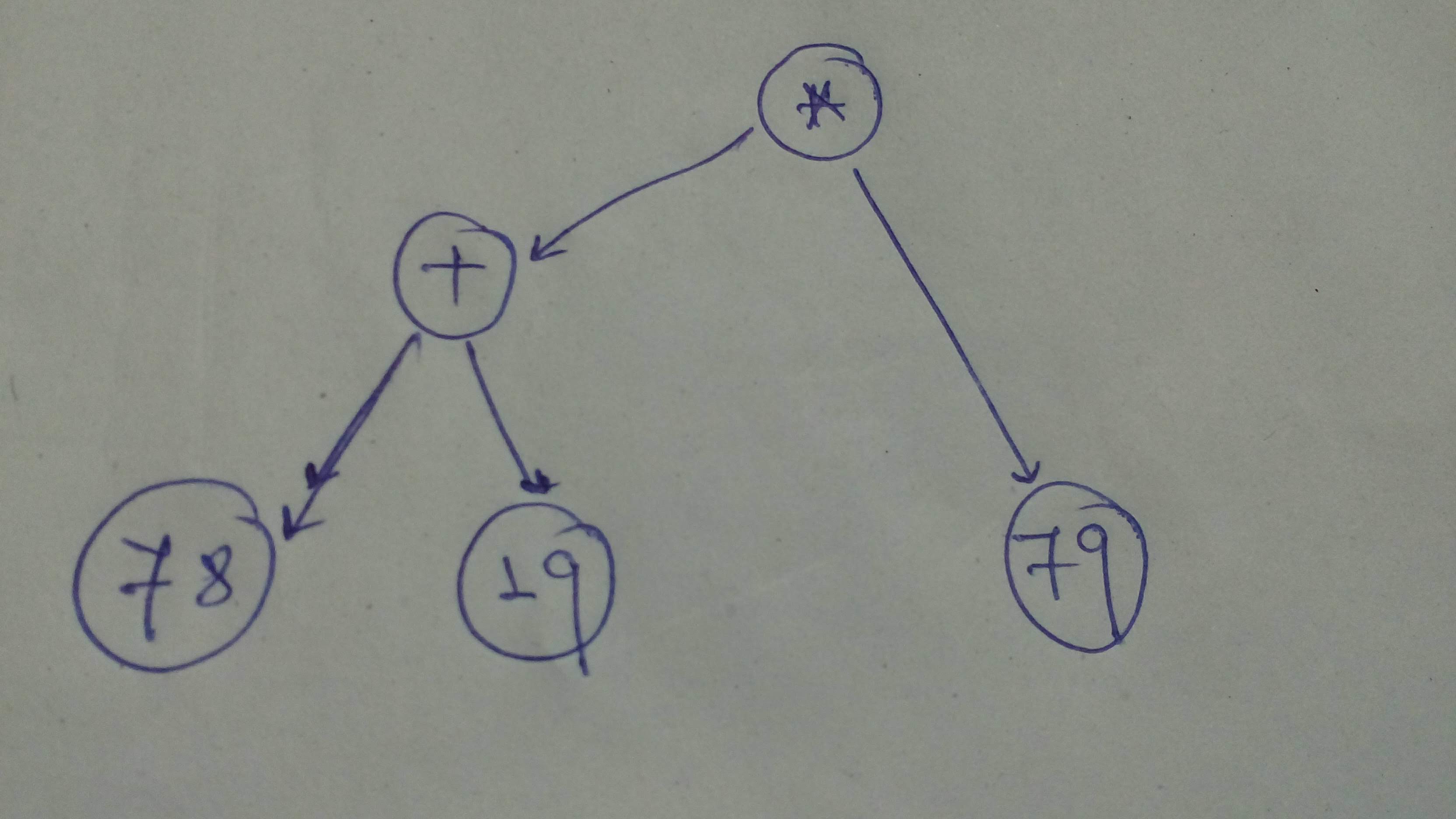"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "FyVz0GNqgreZ",
+ "colab_type": "code",
+ "outputId": "63a0742a-fd87-44b6-d342-472ec473a85f",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 52
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the graph\n",
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "\n",
+ "# Alternatively\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "\n",
+ "# Let's execute using session\n",
+ "sess = tf.Session()\n",
+ "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
+ "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
+ "sess.close()"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hVRvZxrnokUw",
+ "colab_type": "code",
+ "outputId": "cfbffea2-424a-4ddb-d4ad-4d39f3f894db",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 69
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "comp_graph_1_mix = (tf.constant(78) + 19) * 79\n",
+ "raw_ints = 78 + 10 * 79\n",
+ "int_string = \"78 + 10 * 79\"\n",
+ "s = tf.Session()\n",
+ "print('Comp Graph 1 :', s.run(comp_graph_1))\n",
+ "print('Comp Graph 1 Alt:', s.run(comp_graph_1_alt))\n",
+ "print('Comp Graph 1 mix:', s.run(comp_graph_1_mix))\n",
+ "#print('Comp Graph 1 raw:', s.run(raw_ints))\n",
+ "#print('Comp Graph 1 str:', s.run(int_string))\n"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n",
+ "Comp Graph 1 mix: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "SVMMtuFYhaQB",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's define a sligtly more involved graph!\n",
+ "\n",
+ "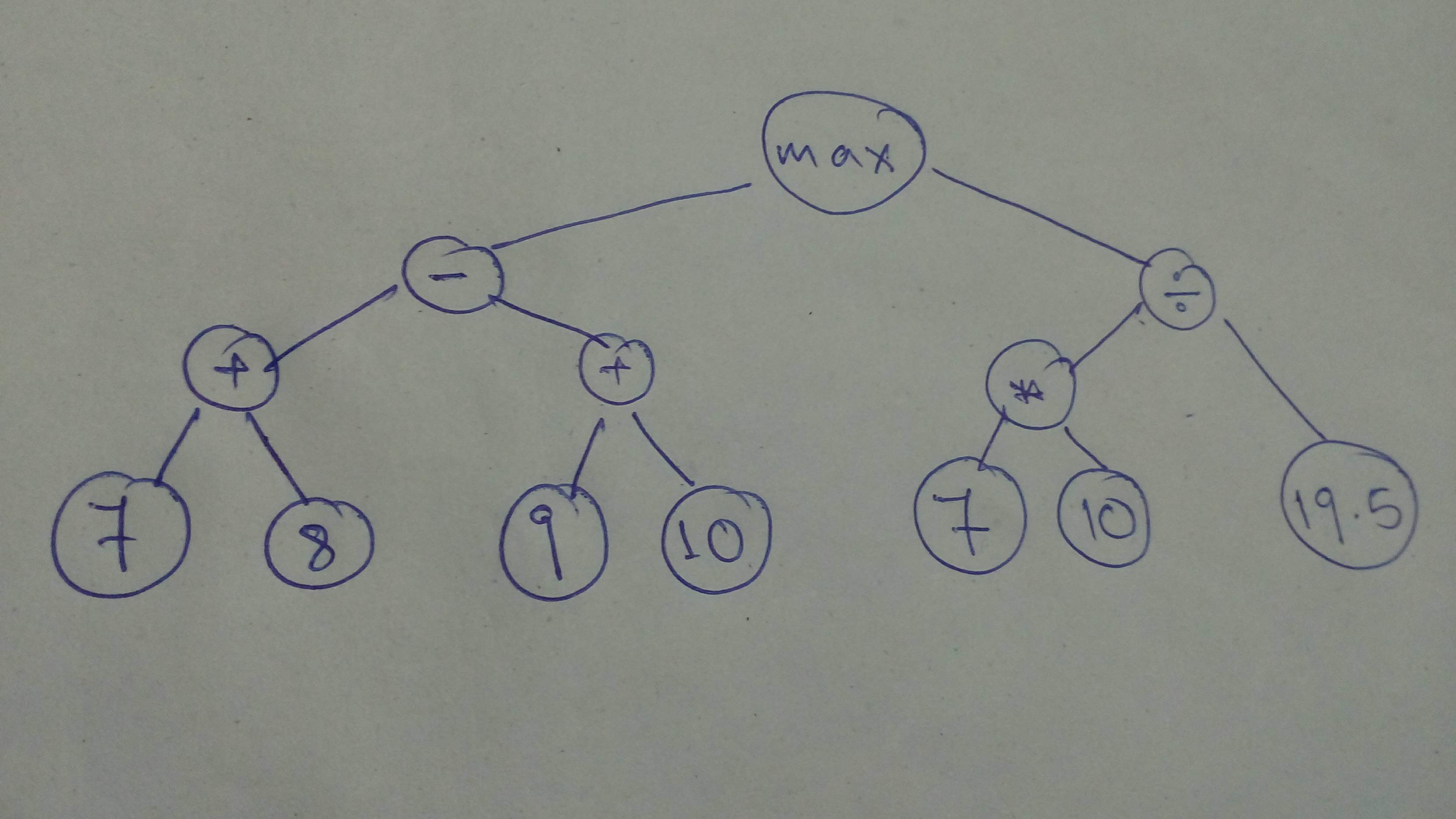"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4856BTvRhiBb",
+ "colab_type": "code",
+ "outputId": "988227d2-bc1a-4f91-9bc3-7808b2b06f0a",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 69
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let build the graph\n",
+ "# We need to cast cause the tensors operated on should be of the same type\n",
+ "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
+ " dtype=tf.float32)\n",
+ "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
+ "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "# Let's execute\n",
+ "sess = tf.Session()\n",
+ "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', part1_res)\n",
+ "print ('Part 2 Result: ', part2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "B-_ZDtEbj4N0",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Cool! Let's go! Build another graph and execute it with sessions.
\n",
+ "\n",
+ "But this time, it's all you!\n",
+ "\n",
+ "Build this graph and execute it with `session`!\n",
+ "\n",
+ "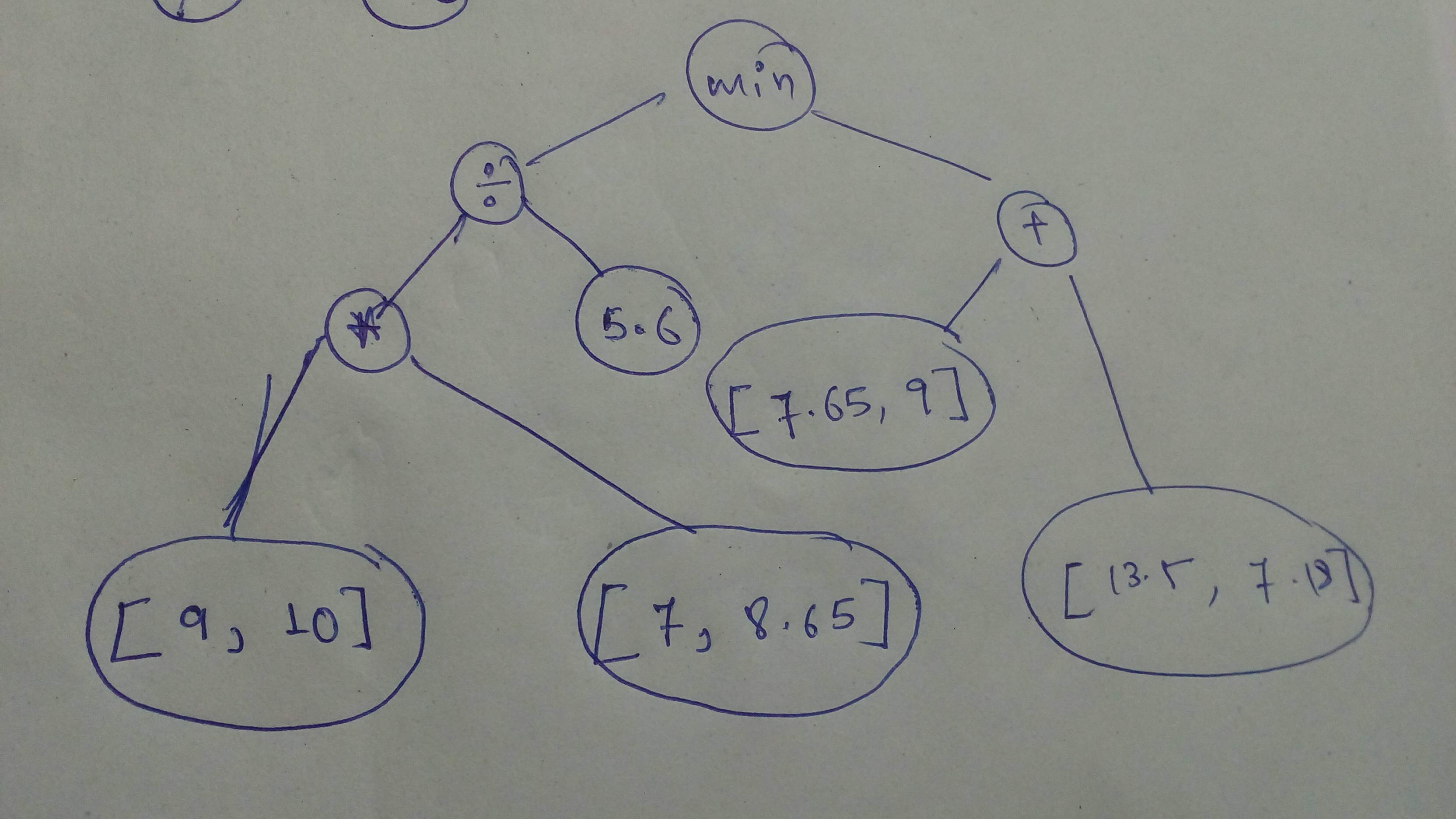\n",
+ "\n",
+ "_Remember that `tensors` operated on should be of the same type!_
\n",
+ "_Search up errors and other help you need on Google_"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "-uHNe1BolJY0",
+ "colab_type": "code",
+ "outputId": "58f51b22-04c8-41ba-d54c-cc0c60bebc36",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 86
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "A = tf.constant([9, 10], dtype=tf.float32)\n",
+ "B = tf.constant([7, 8.65], dtype=tf.float32)\n",
+ "C = tf.constant(5.6)\n",
+ "D = tf.constant([7.65, 9], dtype=tf.float32)\n",
+ "E = tf.constant([13.5, 7.18], dtype=tf.float32)\n",
+ "\n",
+ "mul = tf.multiply(A,B)\n",
+ "div = tf.divide(mul, C)\n",
+ "add = tf.add(D,E)\n",
+ "min_ = tf.math.minimum(div,add)\n",
+ "\n",
+ "\n",
+ "# Execute \n",
+ "sess = tf.Session()\n",
+ "mul_res, div_res, add_res, min_res = sess.run([mul, div, add, min_])\n",
+ "print(\"mul : \", mul_res)\n",
+ "print(\"div: \", div_res)\n",
+ "print(\"add: \", add_res)\n",
+ "print(\"min: \", min_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "mul : [63. 86.5]\n",
+ "div: [11.25 15.446429]\n",
+ "add: [21.15 16.18]\n",
+ "min: [11.25 15.446429]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "qmap38WelREN",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's do another!
\n",
+ "It's fun! Isn't it?!\n",
+ "\n",
+ "Build and execute this one!\n",
+ "\n",
+ "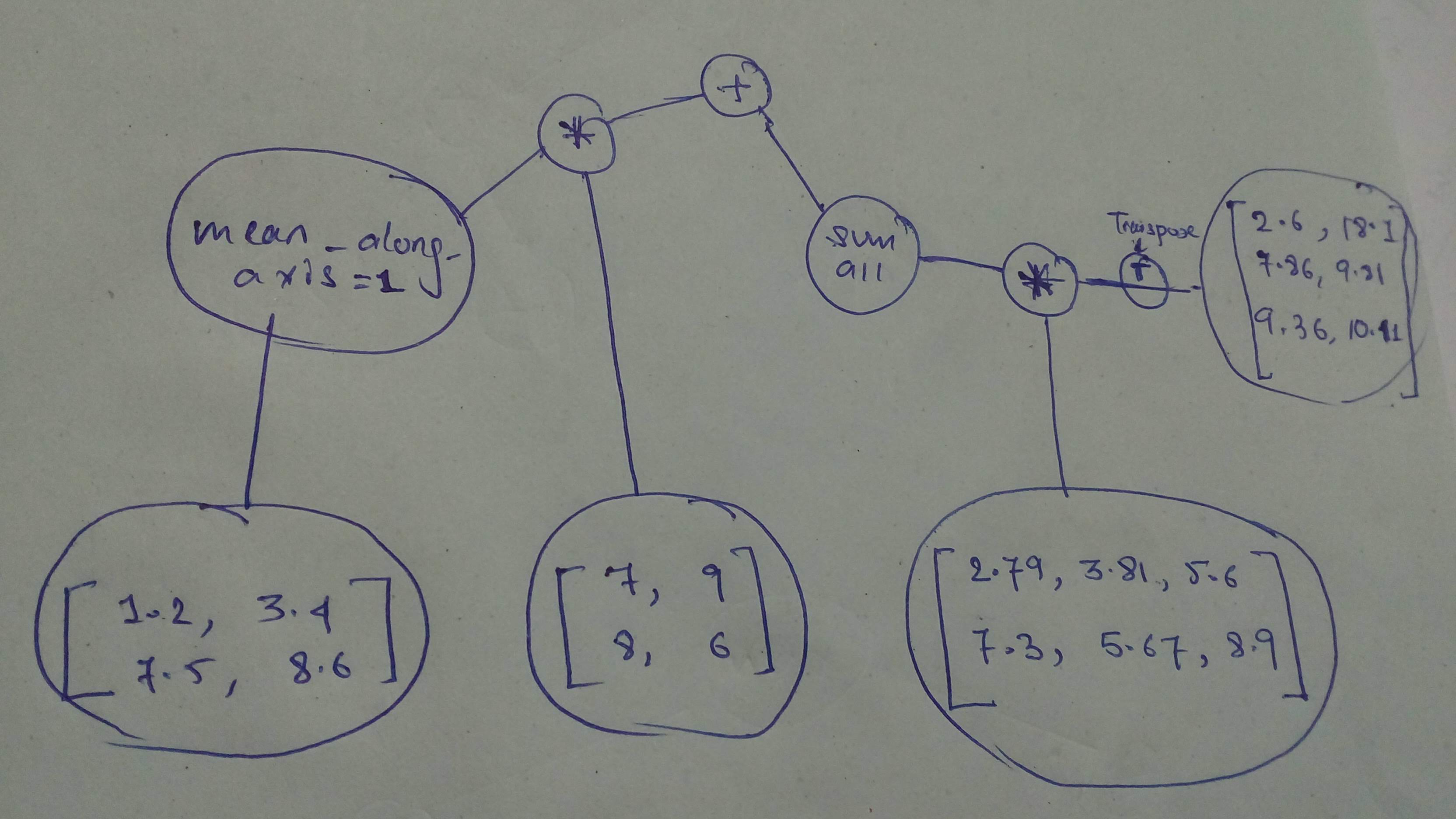"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "0ZhYwAlLmEvB",
+ "colab_type": "code",
+ "outputId": "d3cef926-d9d9-46d4-9cda-2398fbebd08b",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 156
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "A = tf.constant([\n",
+ " [1.2, 3.4],\n",
+ " [7.5, 8.6]\n",
+ "])\n",
+ "B = tf.constant([\n",
+ " [7, 9],\n",
+ " [8,6]\n",
+ "], dtype=tf.float32)\n",
+ "C = tf.constant([\n",
+ " [2.79, 3.81, 5.6],\n",
+ " [7.3, 5.67, 8.9]\n",
+ "])\n",
+ "D = tf.constant([\n",
+ " [2.6, 18.1],\n",
+ " [7.86, 9.81],\n",
+ " [9.36, 10.11]\n",
+ "])\n",
+ "mean = tf.math.reduce_mean(A, axis=1)\n",
+ "mul_1 = tf.multiply(mean,B)\n",
+ "mul_2 = tf.multiply(C, tf.transpose(D))\n",
+ "sum_all = tf.math.reduce_sum(mul_2)\n",
+ "add = tf.add(mul_1,sum_all)\n",
+ "\n",
+ "# Execute \n",
+ "sess = tf.Session()\n",
+ "mean_res, mul_1_res, mul_2_res, sum_all_res, add_res = sess.run([mean, mul_1, mul_2, sum_all, add])\n",
+ "print(\"Mean :\", mean_res)\n",
+ "print(\"Mul 1 :\", mul_1_res)\n",
+ "print(\"Mul 2 :\", mul_2_res)\n",
+ "print(\"Sum all:\", sum_all_res)\n",
+ "print(\"Add :\", add_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Mean : [2.3000002 8.05 ]\n",
+ "Mul 1 : [[16.100002 72.450005]\n",
+ " [18.400002 48.300003]]\n",
+ "Mul 2 : [[ 7.2539997 29.9466 52.415997 ]\n",
+ " [132.13 55.622704 89.979 ]]\n",
+ "Sum all: 367.3483\n",
+ "Add : [[383.4483 439.7983 ]\n",
+ " [385.7483 415.64832]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "BnB0b6qCmGmg",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "And a final one, before we move on to the next part!\n",
+ "\n",
+ "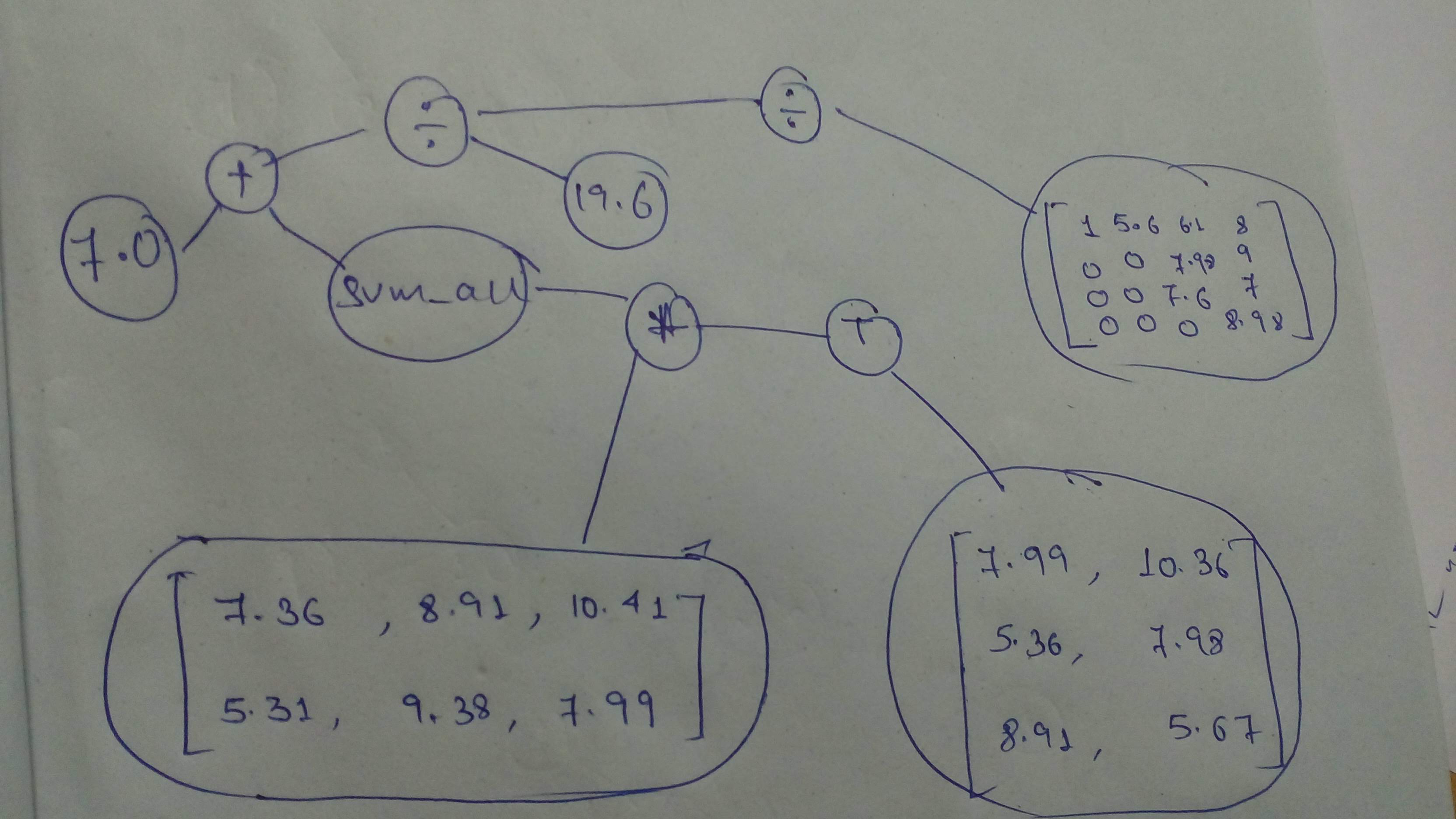"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "GQWyCvsQmMcL",
+ "colab_type": "code",
+ "outputId": "73aa40c9-c9bc-481e-f0af-5d8130d9700e",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 173
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "A = tf.constant(7.0)\n",
+ "B = tf.constant([\n",
+ " [7.36, 8.91, 10.41],\n",
+ " [5.31, 9.38, 7.99]\n",
+ "])\n",
+ "C = tf.constant([\n",
+ " [7.99, 10.36],\n",
+ " [5.36, 7.98],\n",
+ " [8.91, 5.67]\n",
+ "])\n",
+ "D = tf.constant([\n",
+ " [1, 5.6, 6.1, 8],\n",
+ " [0, 0, 7.98, 9],\n",
+ " [0, 0, 7.6, 7],\n",
+ " [0, 0, 0, 8.98]\n",
+ " ])\n",
+ "mul = tf.multiply(B, tf.transpose(C))\n",
+ "sum_all = tf.math.reduce_sum(mul)\n",
+ "add = tf.add(A, sum_all)\n",
+ "divide_1 = tf.divide(add, tf.constant(19.6))\n",
+ "divide_2 = tf.divide(divide_1, D)\n",
+ "\n",
+ "\n",
+ "# Execute \n",
+ "sess = tf.Session()\n",
+ "mul_res, sum_all_res, add_res, divide_1_res, divide_2_res = sess.run([\n",
+ " mul, sum_all, add, divide_1, divide_2\n",
+ "])\n",
+ "print(mul_res)\n",
+ "print(sum_all_res)\n",
+ "print(add_res)\n",
+ "print(divide_1_res)\n",
+ "print(divide_2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[[58.8064 47.7576 92.7531 ]\n",
+ " [55.011597 74.8524 45.3033 ]]\n",
+ "374.48438\n",
+ "381.48438\n",
+ "19.463488\n",
+ "[[19.463488 3.475623 3.1907358 2.432936 ]\n",
+ " [ inf inf 2.4390335 2.1626098]\n",
+ " [ inf inf 2.5609853 2.7804983]\n",
+ " [ inf inf inf 2.1674263]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "J3T5oBzlP1ik",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ ""
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "12NC7XTPsJw7",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# Linear Regression\n",
+ "\n",
+ "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
+ "\n",
+ "\n",
+ "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hW31RZkjtNwI",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Create the dataset\n",
+ "X = np.linspace(-30.0, 300.0, 300)\n",
+ "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Normalize the dataset\n",
+ "X = X / np.max(X)\n",
+ "Y = Y / np.max(Y)\n",
+ "\n",
+ "# Divide it into train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "LQKy6U33y4lt",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the hyperparameters\n",
+ "learning_rate = 0.00001\n",
+ "n_epochs = 60\n",
+ "interval = 20"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "1h1-D8K1uT48",
+ "colab_type": "code",
+ "outputId": "fbaa9304-7a6e-452e-87a4-e127834f8766",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 351
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# let's viz the first 10 datapoints of the dataset\n",
+ "plt.plot(train_X[:10], train_Y[:10], 'g')\n",
+ "plt.show()"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFOCAYAAAB9mZ/eAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3XlcVQX+//HXZbmyCAgIauWeS7ni\nOkHY6EQqZduIRWlR1GSaOeXMSNhkiyXNaJlp88uydEwtacrMFG0hyyQ3FJfSbDFNCu9VEAHZz+8P\nkxm+pugVOHd5Px8PHyP3nnPu+9OpeXOWe6/FMAwDERERcUleZgcQERERx6nIRUREXJiKXERExIWp\nyEVERFyYilxERMSFqchFRERcmI8jK1VUVJCSkkJubi7e3t5Mnz6d1q1b11pmxYoVLFy4EC8vL0aN\nGkVCQgJ5eXmkpqZSXl5OdXU1jzzyCN27d2fIkCG0bNkSb29vAGbMmEGLFi0ufDoRERE351CRr1y5\nkuDgYGbOnMn69euZOXMms2bNqnm+pKSEuXPn8vbbb+Pr68vIkSOJi4tjwYIFxMXFceutt5Kdnc3z\nzz/P/PnzAXjllVcIDAysn6lEREQ8hEOn1rOysoiLiwMgOjqa7OzsWs/n5OTQo0cPgoKC8PPzo0+f\nPmRnZxMaGkpBQQEAhYWFhIaGXmB8ERERz+bQEbndbicsLAwALy8vLBYL5eXlWK3W054HCAsLw2az\nkZSUxMiRI1m+fDlFRUUsXbq0ZpmpU6dy6NAh+vbty6RJk7BYLBcyl4iIiEeos8jT09NJT0+v9VhO\nTk6tn+v6lNdTz7/66qsMHz6c+++/n8zMTJ599lnmzJnDgw8+SGxsLCEhIYwfP541a9YwbNiwM27P\nZjteV+zzFhoaQH5+Sb1v15lpZs/giTODZ86tmd1bRETQbz5e56n1hIQEli1bVuvPTTfdhM1mA07e\n+GYYRs3ROEBkZCR2u73m58OHDxMZGUl2djaxsbEAxMTEsGvXLgBuvPFGwsPD8fHxYdCgQXzzzTeO\nT+ogHx/vRn9Ns2lmz+CJM4Nnzq2ZPZND18hjYmLIyMgAIDMzk4EDB9Z6vlevXuzcuZPCwkKKi4vJ\nzs6mX79+tG3btuZofseOHbRt25bjx4+TnJxMeXk5AJs3b6ZTp04XMpOIiIjHcOgaeXx8PBs2bCAx\nMRGr1UpaWhoA8+bNo3///kRFRTFp0iSSk5OxWCyMHz+eoKAg7rvvPqZMmVLzS8CUKVMICgpi0KBB\n3HLLLTRp0oTLL7/8rKfVRURE5L8srvg1pg1xjTwiIqhBtuvMNLNn8MSZwTPn1szuzeFr5CIiIuK8\nVOQiIiIuTEUuIiLiwlTkIiIiLkxFLiIi4sJU5CIiIi5MRS4iIuLCVOQiIiL1pNqoZvMvG1n69RtU\nVlc2yms69MluIiIiclJJRQmfH1pHxg8fsGb/auwnTn4XSZewrvRp0a/BX19FLiIicp5sJTY+/DGD\njP2rWHfwE05UngCguX8Et192ByM63tAoJQ4qchERkXOyL/8bMvavIuOHD9jyyyYMTn7CeefQLgxt\nF8+w9vH0ieyHt1fjfiObilxEROQ3VFVXsfmXjWTsX8Wa/av4ruBbALwsXgxsdQXD2l/LsHbD6dDs\nUlNzqshFRER+VVxRzKcHPyHjhw/46Mc1HCk9AkCATyDXdrieoe2GE9d2GOH+4SYn/S8VuYiIeLS8\n4l9Ys381a/av4rOfPqWsqgyAFgEtGXP5XQxvH8+VF1+Fn4+fyUl/m4pcREQ8imEY7Dn6NWt+vd6d\nfXhrzXOXhV3OsPbxDG0XT+/IPnhZnP9d2ipyERFxe5XVlWz8OYuMHz4gY/8qfizcD4C3xZsrLx7E\n0HbDGdounnYh7c0N6gAVuYiIuKWi8uN8cuAjMvav4qMf11BQVgBAoG9Tru94E8Pax/OHNnGE+oWZ\nnPTCqMhFRMRt5BYdYs3+1WT88AFfHPqc8upyAC4KvJibOo1kaLt4Yi6OpYl3E5OT1h8VuYiIuCzD\nMNhl31nzqWo5tm01z3UL78Gw9vEMb38tPZr3wmKxmJi04ajIRUTEpVRUVbAhdz1r9q/iwwMZ/Hjs\nRwB8vHwYdMlghrUbztD28bQOamNy0sahIhcREad3rKzg5PXuHz7g4wMfUVh+DIDgJsHcdOkfGdb+\nWoa0uZqQJs1MTtr4VOQiIuK0svO28MzGp9iQ+3nNt4ld0rQ1o7rcyrD21zKi51COHS0zOaW5VOQi\nIuKU1h3M5M7ViZRUltArIoqh7YYzrP21dAvvXnO92+ptBVTkIiIiTuWD79/nvrV3AbBw+FKGt7/W\n5ETOy/k/skZERDzKW3uWcM+aO/Dx8mXJdW+rxOugIhcREacxf+c8JnwylqbWIN6+/j0GXfJ7syM5\nPZ1aFxER0xmGwQvZM3lm45NE+EeybMRyujXvbnYsl6AiFxERUxmGwZNZjzF3+wtc0rQ1b1//nunf\n8e1KVOQiImKaquoqJn82iX9/9Rodm13K2yNWcHHQJWbHcikqchERMUVFVQUTPrmPd/a9TffmPXnr\nuneJCIgwO5bLUZGLiEijO1F5gnvX3MnaHzPo33IgS65N98hPZasPKnIREWlUReXHGbPqVr7I/Zyr\nLhnMguFLCPQNNDuWy1KRi4hIozlaeoTElX9k2+Fs4tuP4OVrXnOrrxQ1g95HLiIijSKv+BduWn4t\n2w5nc0uX23h16EKVeD1QkYuISIP7sXA/1717DV8f/Yp7etzHC0NewsdLJ4Xrg0P/FCsqKkhJSSE3\nNxdvb2+mT59O69atay2zYsUKFi5ciJeXF6NGjSIhIYGSkhJSUlKw2+34+/uTlpZGREQEe/bs4fHH\nHwegS5cuPPHEExc8mIiIOIdvju4l4f0b+Lk4l4f7/pXJAx6t+dITuXAOHZGvXLmS4OBgli5dytix\nY5k5c2at50tKSpg7dy4LFixg0aJFLFy4kIKCApYtW0br1q1ZsmQJ999/P7Nnzwbg6aefJjU1lTff\nfJOioiLWrVt34ZOJiIjpdti2c8PyYfxcnMvUK6aRMvDvKvF65lCRZ2VlERcXB0B0dDTZ2dm1ns/J\nyaFHjx4EBQXh5+dHnz59yM7OZv/+/fTs2ROAfv36sXXrVsrLyzl06FDN44MHDyYrK+tCZhIRESfw\nZe4GbnrvOo6WHmXm72czPupBsyO5JYdOrdvtdsLCwgDw8vLCYrFQXl6O1Wo97XmAsLAwbDYbnTt3\nZt26dQwdOpRNmzaRm5tLfn4+wcHBNcuGh4djs9nO+vqhoQH4+Hg7Ev2sIiKC6n2bzk4zewZPnBk8\nc25nmTnj2wxuWXkzFdUVLPnjEm7tfmuDvZazzGyWOos8PT2d9PT0Wo/l5OTU+tkwjLNu49TzI0eO\nZO/evSQmJjJgwIBaZX+u2wLIzy+pc5nzFRERhM12vN6368w0s2fwxJnBM+d2lpnf/245Yz9Mxtvi\nzcJhS/hDi2ENlstZZm4MZ/qFpc4iT0hIICEhodZjKSkp2Gw2unbtSkVFBYZh1ByNA0RGRmK322t+\nPnz4ML1798ZqtdbcyFZcXMzHH39MWFgYBQUFNcvm5eURGRl5ftOJiIhTWPL1Ih7+dAL+PgEsjl9G\n9MVXmh3J7Tl0jTwmJoaMjAwAMjMzGThwYK3ne/Xqxc6dOyksLKS4uJjs7Gz69evHunXrmDVrFnDy\nrvbY2Fh8fX3p0KEDW7ZsAWDt2rXExsZeyEwiImKCl3Pm8ufM8YRYQ3jn+vdV4o3EoWvk8fHxbNiw\ngcTERKxWK2lpaQDMmzeP/v37ExUVxaRJk0hOTsZisTB+/HiCgoIYOHAgixcvZtSoUYSEhPDcc88B\nkJqaymOPPUZ1dTW9evUiOjq6/iYUEZEGZRgGM7ak8c/N02kR0JL069+ja9hlZsfyGBbjXC5KO5mG\nuB7iSddZTtHMnsETZwbPnNuMmQ3D4LENqbycM5c2we14e8R7tAtp32iv70n72eFr5CIiIr+lqrqK\nSZ8+yJI9i+gc2oX0Ee/RqulFZsfyOCpyERE5b+VV5Yz76F5WfPcuvSKiePO6dwj3Dzc7lkdSkYuI\nyHkpqSjh7jWj+eTAR1xxUQxvxL9FkDW47hWlQajIRUTknBWWHWP0qlv48ucN/KFNHPOHLiLAN8Ds\nWB5NRS4iIufkyIkj3LLyJnbYtnN9x5t46epXsHpb615RGpS+xlREROr0c1EuNywfxg7bdm6/7A5e\njntNJe4kVOQiInJWPxz7nhHvDuWb/L2M7fUAz/3+Rby96v/7LsQxOrUuIiJn9PWRrxj1/o3klfzC\n3/qnMqnfZH0NqZNRkYuIyG/alreVW1feTH5ZPtNi0vhTr3FmR5LfoCIXEZHTfHHoc0avuoUTlSW8\nMPglEi8bbXYkOQMVuYiI1LJ2/2qS19xBtVHNK9csYETHG82OJGehIhcRkRrv7nub8R//CV8vXxYO\nX8qQNlebHUnqoLvWRUQEgH/vfp2xHybj7xPAWyOWq8RdhIpcRESYs+0F/rJuImF+Ybx7w0p+1+oK\nsyPJOdKpdRERD2YYBmmbnuL5rTNoFXgRb1+/gk6hnc2OJedBRS4i4qGqjWoeXT+ZV3e+TLvg9rx9\n/QraBLc1O5acJxW5iIgHqqyu5M+Z41m2dymXhV3OshHLaRHY0uxY4gAVuYiIhymrKuO+tXez6of3\n6RPZl6XX/YdQvzCzY4mDVOQiIh6kuKKYpNW3se6nTK68eBD/Hr6UptYgs2PJBVCRi4h4iGNlBdz2\nQQKbf9nI0HbDeeWahfj5+JkdSy6Q3n4mIuIhHvj4Pjb/spGbOyXw2tA3VOJuQkfkIiIeYO3+1azZ\nv5roi67kpatfwcui4zh3oT0pIuLmSitLmbJ+Mt4Wb6bHzlCJuxntTRERNzd3+wv8WLife3qO5bLw\ny82OI/VMRS4i4sYOFP7IC1tnEhnQgr/1f8TsONIAdI1cRMSN/f2LRyitKmXmFbMJsgabHUcagI7I\nRUTc1CcHPmT1DysZ2OoKRna+xew40kBU5CIibqisqoxHPv8rXhYvpsfOwGKxmB1JGoiKXETEDf1r\n+4v8cOx77u5+L92b9zA7jjQgFbmIiJv56fhBnt/6T5r7RzB5wBSz40gD081uIiJuZuqGKZyoPMGz\ng54jpEkzs+NIA9MRuYiIG1l3MJP3v1tOvxYDGNUl0ew40ghU5CIibqK8qpxHPv8LXhYvnh00U5/g\n5iG0l0VE3MSsL2fxbcE+7ux2Nz0iepkdRxqJQ9fIKyoqSElJITc3F29vb6ZPn07r1q1rLbNixQoW\nLlyIl5cXo0aNIiEhgZKSElJSUrDb7fj7+5OWlkZERARjxoyhpKSEgIAAACZPnkz37t0vfDoREQ+R\nW3SIJ9c9SZhfGCkDHjU7jjQih4p85cqVBAcHM3PmTNavX8/MmTOZNWtWzfMlJSXMnTuXt99+G19f\nX0aOHElcXBzLly+ndevWzJ49my1btjB79myeeuopAKZPn07nzp3rZyoREQ/z+IYpFFcU81RMGqF+\nYWbHkUbk0Kn1rKws4uLiAIiOjiY7O7vW8zk5OfTo0YOgoCD8/Pzo06cP2dnZ7N+/n549ewLQr18/\ntm7deoHxRURk/aHPWP7tOwy4eAC3XTbG7DjSyBwqcrvdTljYyd/4vLy8sFgslJeX/+bzAGFhYdhs\nNjp37sy6desA2LRpE7m5uTXLzJ49m9tvv53HHnuM0tJSh4YREfE0FVUVPPLZX7BgYW78XN3g5oHq\nPLWenp5Oenp6rcdycnJq/WwYxlm3cer5kSNHsnfvXhITExkwYEBN2d9xxx106dKFNm3aMHXqVBYv\nXkxycvIZtxcaGoCPj3dd0c9bRERQvW/T2Wlmz+CJM4NnzP1c1nPszd/Dn/r8iX4X9TM7jik8YT+f\nTZ1FnpCQQEJCQq3HUlJSsNlsdO3alYqKCgzDwGq11jwfGRmJ3W6v+fnw4cP07t0bq9XKE088AUBx\ncTEff/wxQM1peoAhQ4awatWqs2bKzy85h9HOT0REEDbb8XrfrjPTzJ7BE2cGz5g7r/gXpmY+TmiT\nUB7uffIrSt195v/LE/bzKWf6hcWhczAxMTFkZGQAkJmZycCBA2s936tXL3bu3ElhYSHFxcVkZ2fT\nr18/1q1bV3NT3IoVK4iNjcUwDJKSkigsLARg48aNdOrUyZFYIiIe5fENj1JUcZzU300lzC/c7Dhi\nEofuWo+Pj2fDhg0kJiZitVpJS0sDYN68efTv35+oqCgmTZpEcnIyFouF8ePHExQUxMCBA1m8eDGj\nRo0iJCSE5557DovFwqhRo0hKSsLf358WLVowYcKEeh1SRMTdZOV+wX/2LaNXRBSjL7vT7DhiIotR\n1wVuJ9QQp1E86fTMKZrZM3jizODec1dWV/KHZbF8fXQ3q//4MX1b9Afce+Yz8aSZ6/XUuoiImOe1\nnfP4+uhubus6pqbExXOpyEVEXEheSR7Pbn6GkCbNePSKJ8yOI05ARS4i4kKeynqM4+WFpAx4lOb+\nzc2OI05ARS4i4iI2/vwly/YupXvzniR1O/NnbYhnUZGLiLiAquoqHvn8LwCkxc7E26v+PxRLXJOK\nXETEBSzYPZ9d9h3c0uU2BrQaWPcK4jFU5CIiTs5+wk7apmkEW0P4+xVPmh1HnIyKXETEyU3Lmsqx\nsgImD0glMiDS7DjiZFTkIiJObMsvm1iyZxGXhXXjru73mh1HnJCKXETESVVVV5Fy6ga3QTPw8XLo\nU7XFzanIRUSc1KKvFrDDtp0/dhrFFRfFmB1HnJSKXETECR0tPcL0jU/S1DeIx6OnmR1HnJiKXETE\nCT395ZPkl+Xz1/6P0CKwpdlxxImpyEVEnMz2w9m88dUCuoZdxj097jM7jjg5FbmIiBOpNqpJ+WwS\nBgbTY2fg6+1rdiRxcipyEREnsuTrRWQf3spNl/6RmItjzY4jLkBFLiLiJPJLjzLty6kE+ATyePTT\nZscRF6EiFxFxEtM3PsXR0qNM6j+ZVk0vMjuOuAgVuYiIE9hh287C3a/RqVln7us5zuw44kJU5CIi\nJjt5g9tfMDB4JvafWL2tZkcSF6IiFxEx2bK9S9mSt4kRHW/kqtaDzY4jLkZFLiJiomNlBTyZ9XcC\nfAJ4MvoZs+OIC1KRi4iY6NlNT2M/Yeehvn/l4qBLzI4jLkhFLiJikl32nby26xU6hHRkbO8HzI4j\nLkpFLiJiAsMweOTzv1BtVPNM7D9p4t3E7EjiolTkIiImSP/mTTb+nMXw9tcxpM3VZscRF6YiFxFp\nZIVlx3hiw9/x8/bjqZjpZscRF6ciFxFpZP/cPB3bicNM7DuJNsFtzY4jLk5FLiLSiL4+8hWv7nyZ\ndsHtGd97otlxxA2oyEVEGsmpG9yqjCqevvJZ/Hz8zI4kbkBFLiLSSN799m025K5naLvhxLUbZnYc\ncRMqchGRRlBUfpzHNzxKE+8mPBWTZnYccSMqchGRRjBjy7P8UvwzE6Ieol1Ie7PjiBtRkYuINLC9\nR/cwb8dLtAlqy4Q+D5kdR9yMilxEpAEZhkHq53+lsrqSp65Mw9/H3+xI4mZ8HFmpoqKClJQUcnNz\n8fb2Zvr06bRu3brWMseOHePhhx8mMDCQ2bNnn3W9PXv28PjjjwPQpUsXnnjiiQubSkTESaz47l0+\nP7SOP7SJY1i7eLPjiBty6Ih85cqVBAcHs3TpUsaOHcvMmTNPW2bq1Kn07dv3nNZ7+umnSU1N5c03\n36SoqIh169Y5EktExKkUVRQx9YspWL2sPB37DywWi9mRxA05VORZWVnExcUBEB0dTXZ29mnLTJs2\n7bQi/631ysvLOXToED179gRg8ODBZGVlORJLRMSpzNoyg9ziQ4yPepAOIR3NjiNuyqFT63a7nbCw\nMAC8vLywWCyUl5djtVprlmnatOk5rWe32wkODq5ZJjw8HJvNdtbXDw0NwMfH25HoZxUREVTv23R2\nmtkzeOLMYO7ce+17+VfOi7QJacO0oU8Q4BvQKK/rifvaE2f+X3UWeXp6Ounp6bUey8nJqfWzYRgO\nvfhvrXcu28rPL3Ho9c4mIiIIm+14vW/XmWlmz+CJM4O5cxuGwdiV46ioruDx3z1DcUEVxTR8Fk/c\n154085l+YamzyBMSEkhISKj1WEpKCjabja5du1JRUYFhGLWOxs8kMjLytPUiIiIoKCioWSYvL4/I\nyMg6tyUi4qw++P59Pj34Cb9vPYRrO4wwO464OYeukcfExJCRkQFAZmYmAwcOdHg9X19fOnTowJYt\nWwBYu3YtsbGxjsQSETFdSUUJj33xCL5evjxz5T91g5s0OIeukcfHx7NhwwYSExOxWq2kpZ38uMF5\n8+bRv39/evbsSVJSEoWFheTl5TFmzBjGjRt3xvVSU1N57LHHqK6uplevXkRHR9ffhCIijeiF7Bn8\nVHSQCVEPcWloJ7PjiAewGI5e4DZRQ1wP8aTrLKdoZs/giTODOXN/X/Atg978Hc39I1h/22aa+p5+\n029D8sR97Ukzn+kauT7ZTUSkHhiGwZT1kymvLueJmKcbvcTFc6nIRUTqwZr9q/n4wIfEXnwV13e8\nyew44kFU5CIiF+hE5QkeXT8ZHy8fpsfO0A1u0qhU5CIiF+jF7Oc5cPxH/tRzHJ3DupgdRzyMQ3et\ni4jUp71H97A1bzOhfmGE+zWnuX844f7NCbaGOP3R7f5jP/DitudpGdiKv/SbbHYc8UAqchEx1Zr9\nq7l3zZ2UVpWe9pyvly9hfidLPdwvnHD/U39vTrh/c5r/+vcw//CT/+sXhrdX/X9889n8/YsUyqrK\neDx6Gk2tnv1RoWIOFbmImGbZ3qVM/GQcTbyb8GTMM1QbBkdO2E/+KbVj//XvPx0/yFdHdtW5PQsW\nQv1CCfdrTsvgFgT7hBLmF37yCP/X8j/1p/mvvwA08W7icP4P92ewZv9qoi+6kpsuHenwdkQuhIpc\nREwxL+clHv0ihWZNmrH42nT6tzz7J0SWV5VztPRITbkfKbVz9MQR7KV2jpw4UvPYqV8Evi3Yh0Hd\nH5PR1DeIcP/wmqP7U0V/8heAU2cC/vt4oE8gFouF0spSUtf/DW+Lt25wE1OpyEWkURmGwT82P8PM\nLc/SIqAly0Ys57Lwy+tcz+ptpWVgK1oGtjqn1wkLD2DfTwdPO7o/Wnrkfx7779932HKoqK6oc7t+\n3n6E+YVj9bbyY+F+7us57pzyizQUFbmINJpqo5op6//G/J3zaBvcjvQR79EupH2DvJa3l/ev19TD\ngbrvJDcMg6KK4/9zxH+y5O3/W/41R/1HOFxymI7NLuWv/R9pkPwi50pFLiKNoqKqggmfjOWdfelc\nFtaNZSPepUVgS7Nj1bBYLARZgwmyBtM+pIPZcUTOmYpcRBpcSUUJ9669kw9/XEO/FgNYcm06zfxC\nzY4l4hZU5CLSoI6VFTB61S1s/DmLIW2uZv7QRQT6BpodS8RtqMhFpMEcLjnMrStvZpd9BzdeejNz\n/jAPq7fV7FgibkUf0SoiDeJA4Y+MePcadtl3cGe3ZP519XyVuEgD0BG5iNS7vUf3kPD+DfxS/DMP\n9f0LKQP+rvdZizQQFbmI1KvsvC0krvwj+WX5PBH9DPf3fsDsSCJuTUUuIvVm3cFM7lx9G6VVJ3hh\n8EskXjba7Egibk9FLiL1YuV3Kxj74d0AvDb0DeI7XGdyIhHPoJvdROSCLf7q39yz9g58va0sve4/\nKnGRRqQiF5ELMmfbCzz06QM0a9KMd65/n9hLrjI7kohH0al1EXGIYRg8/eUTzN72HK0CLyJ9xHt0\nDqv7M81FpH6pyEXkvFVVV/G3zx5i0VcL6NjsUpaNWE7roDZmxxLxSCpyETkvZVVljP/oT6z47l16\nNO/Fm9e9Q0RAhNmxRDyWilxEzllRRRF3rb6ddT9lcsVFMSwa/ibBTULMjiXi0VTkInJO8kuPctsH\nCWzN28w1bYfxytCF+Pv4mx1LxOOpyEWkTr8U/8wt79/E10e/YmTnW3hh8Ev4evuaHUtE0NvPRKQO\n3x/7juveuYavj37FvT3GMucPL6vERZyIjshF5Ix223cx6v0bsZ04zN/6pzKp32R9+YmIk1GRi8hv\n2vjzl9z+QQKF5ceYHvtPknvcZ3YkEfkNKnIROc3HP67l7jVjKK8q56WrX2Fk51vMjiQiZ6AiF5Fa\n3tmXzgMf34ePxYeFw5dwTbvhZkcSkbPQzW4iUuP1Xa9y/4f34O8TwFsj3lWJi7gAHZGLCIZhMGvr\nDKZveorm/hG8dd079IjoZXYsETkHDhV5RUUFKSkp5Obm4u3tzfTp02ndunWtZY4dO8bDDz9MYGAg\ns2fPPut6Y8aMoaSkhICAAAAmT55M9+7dL3A0ETkX1UY1UzdM4eWcubQOakP6iOV0aHap2bFE5Bw5\ndGp95cqVBAcHs3TpUsaOHcvMmTNPW2bq1Kn07dv3nNebPn06ixYtYtGiRSpxkUZSWV3JxE/G8XLO\nXDqHduH9m9aoxEVcjENFnpWVRVxcHADR0dFkZ2eftsy0adNOK/JzWU9EGkdpZSl3rxnDW3uXEBXZ\nh/duzOCiphebHUtEzpNDp9btdjthYWEAeHl5YbFYKC8vx2q11izTtGnTc14PYPbs2eTn59OxY0dS\nU1Px8/NzJJqInIPj5YXcufo21h/6jNiLr2Lh8CU0tQaZHUtEHFBnkaenp5Oenl7rsZycnFo/G4bh\n0IufWu+OO+6gS5cutGnThqlTp7J48WKSk5PPuF5oaAA+Pt4OvebZRER43v+RaWbP8L8z24ptjHr3\nBrb+vJWbut7Ekj8uwc/HPX9x9vR97Sk8ceb/VWeRJyQkkJCQUOuxlJQUbDYbXbt2paKiAsMwah2N\nn0lkZORvrnfqdDvAkCFDWLVq1Vm3k59fUudrna+IiCBstuP1vl1nppk9w//OfOj4TyS8fwPfFuzj\ntq5jmPH7FzieX8FxKkxOWf88fV97Ck+a+Uy/sDh0jTwmJoaMjAwAMjMzGThwoMPrGYZBUlIShYWF\nAGzcuJFOnTo5EktEzuLb/H1c9+41fFuwj3G9H+T5wXPw8dI7UEVcnUP/FcfHx7NhwwYSExOxWq2k\npaUBMG/ePPr370/Pnj1ryjl0ErC2AAAZeUlEQVQvL48xY8Ywbty431zPYrEwatQokpKS8Pf3p0WL\nFkyYMKFehxTxdDts27nl/Zs4UnqER3/3OBOiHtKXn4i4CYvh6AVuEzXEaRRPOj1zimb2DLuLtzJi\nyfUUVxTxj6ue585ud5sdqVF44r7WzO7tTKfWdV5NxI1l/LCKe9feSbVRzbxrXueGS282O5KI1DN9\n1rqIm3przxLuyrgdby9vFsW/pRIXcVM6IhdxQ/NyXuLRL1IIadKM1bev4lI/fVqiiLvSEbmIm5mx\nOY1Hv0ghMqAF7924mitaX2F2JBFpQDoiF3Eji7/6N//Y/Axtgtvx9oj3aBfS3uxIItLAdEQu4ibW\nH/qMv372Z0KbhLJsxLsqcREPoSIXcQPfFezj7ozRWLCwYPgSOoR0NDuSiDQSnVoXcXFHS49w2wcJ\nFJQVMHvIv7jiohizI4lII9IRuYgLK68q5+6MMfxw7HsejHqYW7vebnYkEWlkKnIRF2UYBn9d92c2\n5K7nug43kPq7x8yOJCImUJGLuKgXt81i6Z436B0RxZw/vIyXRf85i3gi/Zcv4oJWfreCaV9O5aLA\ni1kU/xYBvgFmRxIRk6jIRVzM9sPZjP/4XgJ8Annj2mW0CGxpdiQRMZHuWhdxIblFhxiz6lZKK0v5\nd/ybdG/ew+xIImIyFbmIiyiqKGL0qlvIK/mFJ6KfYWi74WZHEhEnoFPrIi6gqrqKcR/ewy77DsZc\nfhdje403O5KIOAkVuYgLeDLrMTL2r2LQJYNJi52BxWIxO5KIOAkVuYiTW/TVAv6V8yKdmnVm/tCF\n+Hr7mh1JRJyIilzEiX3206dM/uxhwvzCeOPaZYQ0aWZ2JBFxMipyESe1L/8b7s4YgxdeLBi+lPYh\nHcyOJCJOSHetizihIyeOcPsHCRSWH+PFIf+P37W6wuxIIuKkdEQu4mTKqsq4K+N29hf+wEN9/8It\nXW8zO5KIODEVuYgTMQyDSZ8+yJc/b+D6jjcxecCjZkcSESenIhdxIi9kz2TZ3qX0iezLi3/4f/oi\nFBGpk/5fQsRJrPj2XZ7Z+CSXNG3Nwvg38ffxNzuSiLgAFbmIE9iWt5UHPr6PQN+mLIp/ixYBLcyO\nJCIuQneti5jsp+MHGbP6Vsqry1k09N90a97d7Egi4kJU5CImKio/zuhVt3C4JI9pMWnEtRtmdiQR\ncTE6tS5ikqrqKu778G6+OrKLpG7J3NvzfrMjiYgLUpGLmOTxDVP48Mc1/L71EJ6J/ae+CEVEHKIi\nFzHBgl3zeXnHS3QJ7cqr1yzEx0tXuUTEMSpykUb26cFPeOTzv9DcvzlvXLuM4CYhZkcSERemIhdp\nRN8c3cs9a+7E2+LNgmFLaRvczuxIIuLidD5PpJHYT9i5bdXJL0J56epXGNBqoNmRRMQN6IhcpBGU\nVZWRtPo2DhTuZ1K/yYzsfIvZkUTETThU5BUVFUyaNInExERGjx7NwYMHT1vm2LFjJCcn8+CDD9Z6\nfNOmTVxxxRVkZmbWPLZnzx5uvfVWbr31VqZOnepIJBGnZRgGD2U+wKZfvuSmS//I3/qnmh1JRNyI\nQ0W+cuVKgoODWbp0KWPHjmXmzJmnLTN16lT69u1b67EDBw7w+uuv06dPn1qPP/3006SmpvLmm29S\nVFTEunXrHIkl4pSe3/pP3v7mLfq26M8LQ/6lt5mJSL1yqMizsrKIi4sDIDo6muzs7NOWmTZt2mlF\nHhERwZw5cwgKCqp5rLy8nEOHDtGzZ08ABg8eTFZWliOxRJzOe9++Q9qmabQOasPC4Uvx8/EzO5KI\nuBmHbnaz2+2EhYUB4OXlhcVioby8HKvVWrNM06ZNT1vP3//0b3PKz88nODi45ufw8HBsNttZXz80\nNAAfH29Hop9VRERQ3Qu5Gc3ccDb+tJEJn4wlyBrEqtEf0C2yY6O87m/xxP0Mnjm3ZvY8dRZ5eno6\n6enptR7Lycmp9bNhGPUW6Fy2lZ9fUm+vd0pERBA22/F6364z08wN5+DxA1z39gjKq8pZMGwxLSxt\nTftn7Yn7GTxzbs3s3s70C0udRZ6QkEBCQkKtx1JSUrDZbHTt2pWKigoMw6h1NH4+wsLCKCgoqPk5\nLy+PyMhIh7Yl4gyOlxcy+oNR2E/YmB77T4a0iTM7koi4MYeukcfExJCRkQFAZmYmAwc6/n5YX19f\nOnTowJYtWwBYu3YtsbGxDm9PxEyV1ZX8ae1dfH30K5J7/InkHveZHUlE3JxD18jj4+PZsGEDiYmJ\nWK1W0tLSAJg3bx79+/enZ8+eJCUlUVhYSF5eHmPGjGHcuHGUlZUxf/58vv/+e3bv3s2iRYt47bXX\nSE1N5bHHHqO6uppevXoRHR1dr0OKNJapX6Ty8YEP+UObOJ6KSTM7joh4AItRnxe4G0lDXA/xpOss\np2jm+vXarldI+WwSl4Vdzsqb1xJkDa57pUbgifsZPHNuzezeznSNXJ/sJlIPPjnwEVM+/xvN/SN4\n49plTlPiIuL+VOQiF2jP0a+5d20SPl4+/Hv4UloHtTE7koh4EH1pisgFsJXYGP3BKI6XF/Jy3Gv0\naznA7Egi4mF0RC7ioNLKUu5cnciB4z/yt/6p3NRppNmRRMQDqchFHGAYBn/OHMeWvE38sdMoJvWb\nbHYkEfFQKnIRB8zYksY7+96mf8uBPD94jr4IRURMoyIXOU/v7Evnn5un0ya4nb4IRURMpyIXOQ+b\nft7IxE/GEWQNZnH8Mpr7Nzc7koh4ON21LnKOfizcT1JGIpXVlfx7+Jt0CetqdiQRERW5yLkoLDv2\n6xeh2Hl20HMMbvMHsyOJiAA6tS5Sp8rqSu5dm8Te/D38qef93NX9HrMjiYjUUJGL1OHR9ZPJPPgx\ncW2H8kT0M2bHERGpRafWRc6gqrqKl3Je5LVdr3B5eHdejnsNby9vs2OJiNSiIhf5P/JK8lj81UIW\nfbWAQ0U/EeEfyRvxb9HU+tvfPCQiYiYVuQgnP6ltQ+56Fuyazwc/rKCyupJA36bc2S2Zcb0ncElQ\na7Mjioj8JhW5eLRjZQUs27uUhbtf45v8vQBcFtaNpO7JJHS+RUfhIuL0VOTikXIOb2PB7vm8u+9t\nSipLsHpZublTAnd1v5cBLQfqI1dFxGWoyMVjnKg8wYLt/+HFrDlkH94KQJvgdtxx+V3cdtkYfUqb\niLgkFbm4ve8K9rFg92u8tWcxBWUFeFm8GNpuOEndkhnc5mq8LHoXpoi4LhW5uKWKqgoy9q9iwe75\nfP7TpwA0948g9cpU/tj+NloHtTE3oIhIPVGRi1v5uSiXRV8t4I2vF/JL8c8ARF90JUndkonvMIKL\nW4Zjsx03OaWISP1RkYvLqzaq+eynT1mwaz5r9q+iyqgiyBrMPT3u485uyfpyExFxaypycVlHS4/w\n5p4lLNw9nx+OfQ9Aj+a9SOqezM2dEgj0DTQ5oYhIw1ORi0sxDIOteZtZsHs+7337DmVVZfh5+3FL\nl9tI6p5Mn8h+euuYiHgUFbm4hOKKYt7Zl86CXfPZac8BoH1IB+7slsytXW8jzC/c5IQiIuZQkYtT\n23t0Dwt2v8qyvW9yvLwQb4s38e1HkNQ9mUGX/F5vHRMRj6ciF6dTXlXOB9+vYMHu+WTlfgFAy8BW\n3NdzHKMvv5OLml5sckIREeehIhencfD4ARbtPvnWMfsJGwCxl/yeu7rdw9B2w/H19jU5oYiI81GR\ni6mqqqvIPPgRC3bN56MDa6k2qmnWpBn39RpPUre76disk9kRRUScmopcTGErsbF0zyL+vft1Dhz/\nEYCoyD7c1f1ebrj0Zvx9/E1OKCLiGlTk0mgMw2DjL1+yYNerrPzuPcqry/H38ef2y+4gqVsyvSKj\nzI4oIuJyVOTSYEorS9l9ZCfbD29j++FsNv+yke+PfQdAp2adSeqezKguiYQ0aWZyUhER16Uil3pR\nWV3JnqNfs/1w9snitmXz9ZHdVFRX1CwT4BPI9R1v4q7u9xB90ZX64BYRkXqgIpfzVm1U833Bd2w7\nvJXth7PZdjib3Ud2cqLyRM0yVi8rPZr3pHdkH3pH9iEqsi+XNuuEt5e3iclFRNyPilzOyjAMDh4/\nQI5tG9sOZ7P9cDY5tu0cLy+sWcbb4k3XsMvpHRn1a2n3oWvY5Vi9rSYmFxHxDA4VeUVFBSkpKeTm\n5uLt7c306dNp3bp1rWWOHTvGww8/TGBgILNnz655fNOmTUycOJFnnnmGwYMHAzBmzBhKSkoICAgA\nYPLkyXTv3t3RmeQC5JXk/Xp6/FRpb8N+wl5rmUubdWJou+H0joiid2RfujfvQYBvgEmJRUQ8m0NF\nvnLlSoKDg5k5cybr169n5syZzJo1q9YyU6dOpW/fvuzZs6fmsQMHDvD666/Tp0+f07Y5ffp0Onfu\n7EgccVD+iXw+PfgZOYf/e7SdW3yo1jKtg9owouONJ0+RR0TRK6I3wU1CTEosIiL/l0NFnpWVxY03\n3ghAdHQ0qamppy0zbdo0du/eXavIIyIimDNnDlOmTHEwrjiquKKYnbYcth3OJsd28rr2qa/+PCXC\nP5Jr2g6rOT3eMyKKiIAIkxKLiMi5cKjI7XY7YWFhAHh5eWGxWCgvL8dq/e810aZNm562nr//mT/k\nY/bs2eTn59OxY0dSU1Px8/M747KhoQH4+NT/TVMREUH1vk0zlFWWsSNvB5tzN5/8c2gzX9u/ptqo\nrlmmmV8zru5wNf0v6n/yz8X9uTjoYo+4k9xd9vP58MSZwTPn1syep84iT09PJz09vdZjOTk5tX42\nDOOCQtxxxx106dKFNm3aMHXqVBYvXkxycvIZl8/PL7mg1/stERFB2GzH6327Da2yupK9R/fUuhnt\nqyO7Tnvb14CWv6NXZBRRv95F3j64A5GRwf+duQzsZUUmTdF4XHU/XwhPnBk8c27N7N7O9AtLnUWe\nkJBAQkJCrcdSUlKw2Wx07dqViooKDMOodTR+vuLi4mr+PmTIEFatWuXwtjzBj4X7Wbj7NTb9/CW7\n7DsoqfzvLzZWLyvdm/f49Zr2ydLuHNpFb/sSEXFTDp1aj4mJISMjg9jYWDIzMxk4cKDDAQzD4K67\n7mL27NkEBwezceNGOnXSF2X8lp32HczdNov3vn2XKqMKL4sXXUIvqznK7h0ZxWXh3Wji3cTsqCIi\n0kgcKvL4+Hg2bNhAYmIiVquVtLQ0AObNm0f//v3p2bMnSUlJFBYWkpeXx5gxYxg3bhxlZWXMnz+f\n77//nt27d7No0SJee+01Ro0aRVJSEv7+/rRo0YIJEybU65CuzDAM1h/6jBe3Pc+nBz8B4LKwbjwQ\nNZH4DiMI9A00OaGIiJjJYlzoBW4TNMT1EGe7zlJVXcUH369gzrZZbLdtAyDmolgeiJrIkDZx9XJT\nmrPN3Bg0s+fwxLk1s3tz+Bq5NK7SylLe2ruEl7bP5odj32PBwrUdrueBqIn0bdHf7HgiIuJkVORO\noqA0nwW75zNvx7+wn7Bh9bIy5vIk7u81gUtDdc+AiIj8NhW5yXKLDvFyzkv8+6vXKa4oIsgazISo\nh/hTz/tpEdjS7HgiIuLkVOQm2Xt0D3O3v8B/vllGRXUFLQJaMqnfZO7sdhdB1mCz44mIiItQkTey\njT9/yZxtz7Nm/2rg5BeQjO89kZFdbtHbxkRE5LypyBtBtVHNhz+u4cXs59n0y5cA9G3RnwlRDzGs\nfTxeFi+TE4qIiKtSkTeg8qpy3tmXztxtL7A3/+SXx8S1HcoDUX/md62iPeJzzUVEpGGpyBtAUflx\nFn21kJdz5pJbfAgfLx8SOt/K+KiJXB7ezex4IiLiRlTk9ehwyWFe3fH/eH33qxwrKyDAJ5D7eo7j\nvl7juSSotdnxRETEDanI68EPx77npe0v8uaeNyirKiPcL5zJA6Zwd/d7CfULMzueiIi4MRX5Bcg5\nvI0Xt81i5ffvUW1U0ya4HeN6T+DWLrcT4BtgdjwREfEAKvLzZBgG637K5MVts/j8p08B6NG8Fw9E\nTWRExxvx8dI/UhERaTxqnXNUWV3J+98tZ862F9hpzwEg9pLfMyHqz1x1yWDdgS4iIqZQkdfhROUJ\nlu55g39tf5EfC/fjZfHiho4380DURHpFRpkdT0REPJyK/AzyS4/y2q5XmL/zZewn7DTxbsKd3ZK5\nv/cDdAjpaHY8ERERQEV+mp+OH+TlnLks+mohJZXFhDRpxkN9/0Jyj7FEBkSaHU9ERKQWFfmvdh3e\nxZMfP827375NZXUlrQIvYvKAKYy5/E6aWn/7y9xFRETM5vFFXlxRzLiP7mX1DysB6BLalfFRE7m5\nUwJWb6vJ6URERM7O44vcfsJG5oGPiGkdw9geDxLXdqi+xERERFyGxxd52+B2fH9vLq1ahGKzHTc7\njoiIyHnRoSfoQ1xERMRlqchFRERcmIpcRETEhanIRUREXJiKXERExIWpyEVERFyYilxERMSFqchF\nRERcmIpcRETEhanIRUREXJiKXERExIWpyEVERFyYxTAMw+wQIiIi4hgdkYuIiLgwFbmIiIgLU5GL\niIi4MBW5iIiIC1ORi4iIuDAVuYiIiAtTkYuIiLgwH7MDNLSKigpSUlLIzc3F29ub6dOn07p161rL\nHDt2jIcffpjAwEBmz5591vX27NnD448/DkCXLl144oknGnukOp3LzCtWrGDhwoV4eXkxatQoEhIS\nKCkpISUlBbvdjr+/P2lpaURERDBmzBhKSkoICAgAYPLkyXTv3t2M0c6ovmd25/2cl5dHamoq5eXl\nVFdX88gjj9C9e3eGDBlCy5Yt8fb2BmDGjBm0aNHCjNHOqr7n3rBhA8899xze3t4MGjSI8ePHmzTZ\nmTk687/+9S82bNgAQHV1NXa7nTVr1rjEvq7vmV1hPzvMcHPvvPOO8fjjjxuGYRiff/65MXHixNOW\nmThxojF37lxjwoQJda43evRoIycnxzAMw3j44YeNTz/9tKFHOG91zVxcXGxcc801RmFhoXHixAnj\n2muvNfLz843XX3/d+Mc//mEYhmFs3rzZePTRRw3DODnz3r17G3eI89QQM7vrfk5LSzOWLl1qGIZh\nbN261bj77rsNwzCMwYMHG0VFRY07hAPqe+7hw4cbubm5RlVVlZGYmGjs27evcQc6B47O/H+38cor\nrxiG4Rr7ur5ndoX97Ci3P7WelZVFXFwcANHR0WRnZ5+2zLRp0+jbt2+d65WXl3Po0CF69uwJwODB\ng8nKymrgCc5fXTPn5OTQo0cPgoKC8PPzo0+fPmRnZ7N///6a2fr168fWrVsbPbuj6nNmd9/PoaGh\nFBQUAFBYWEhoaGijZ78Q9Tn3wYMHCQkJoVWrVnh5eXHVVVe51b4+pbKykqVLlzJ69OhGzX0h6nNm\nV9nPjnL7U+t2u52wsDAAvLy8sFgslJeXY7Vaa5Zp2rTpOa1nt9sJDg6uWSY8PBybzdbAE5y/umb+\n3+cBwsLCsNlsdO7cmXXr1jF06FA2bdpEbm5uzTKzZ88mPz+fjh07kpqaip+fX+MOVYf6nDk/P9+t\n93NSUhIjR45k+fLlFBUVsXTp0pplpk6dyqFDh+jbty+TJk3CYrE07lDnoD7nttlspy178ODBxh3o\nHDg68ylr167lyiuvrPXfrbPv6/qc2VX2s6PcqsjT09NJT0+v9VhOTk6tnw0HP1r+t9ZzdFv1qT5m\nPvX8yJEj2bt3L4mJiQwYMKDmX/w77riDLl260KZNG6ZOncrixYtJTk6uxynOT2PMfD7bagz1OfOr\nr77K8OHDuf/++8nMzOTZZ59lzpw5PPjgg8TGxhISEsL48eNZs2YNw4YNq99BzlNDz3333XfXb+B6\nUJ8zn/Kf//yn1n0ezravG2Nmd+ZWRZ6QkEBCQkKtx1JSUrDZbHTt2pWKigoMw6h1NH4mkZGRp60X\nERFRc2oOIC8vj8jIyHqf43w4MnNkZCR2u73m58OHD9O7d2+sVmvNv/jFxcV8/PHHADWntwCGDBnC\nqlWrGnKkOjX0zGFhYW69nz/88EP+/Oc/AxATE1Mz/4033liz7KBBg/jmm29ML/KGnvv/Lutu+xqg\npKSEX375hUsuuaTmeWfb1w09szPu5/rk9tfIY2JiyMjIACAzM5OBAwc6vJ6vry8dOnRgy5YtwMlT\nN7GxsQ0T/ALUNXOvXr3YuXMnhYWFFBcXk52dTb9+/Vi3bh2zZs0CTt4NGhsbi2EYJCUlUVhYCMDG\njRvp1KlT4w50DupzZnffz23btq052tmxYwdt27bl+PHjJCcnU15eDsDmzZudcj9D/c59ySWXUFRU\nxE8//URlZSWZmZnExMQ0+kx1cXRmgD179tChQ4eaZV1lX9fnzK6ynx3l9l9jWlVVxaOPPsr+/fux\nWq2kpaXRqlUr5s2bR//+/enZs2dNUeXl5dGpUyfGjRvHgAEDfnO9b7/9lscee4zq6mp69erFI488\nYvaIp6lr5qioKDIyMpg/fz4Wi4XRo0dz/fXXU1payoMPPkhBQQEhISE899xzBAUFsWrVKl599VX8\n/f1p0aIFTz/9NP7+/maPWUt9z+zO+/nw4cNMmTKF0tJSAKZMmULXrl1ZuHAhy5cvp0mTJlx++eX8\n/e9/d7rrplD/c2/evJkZM2YAcM0115h62ehMHJ0ZqHnr1f+eZnaFfV3fM7vCfnaU2xe5iIiIO3P7\nU+siIiLuTEUuIiLiwlTkIiIiLkxFLiIi4sJU5CIiIi5MRS4iIuLCVOQiIiIu7P8DkZOqOWQK6d4A\nAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jrsUps0nu8vj",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "** Question **
\n",
+ "Why did I created a session to plot the graph?
\n",
+ "[Ans]"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "P3-iuxE4sjAf",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the placeholders\n",
+ "\n",
+ "# Placeholders?\n",
+ "# The input to the model changes on iteration\n",
+ "# So we cannot have a constant in the input as we did before\n",
+ "# And thus we need placeholders which we can change on each \n",
+ "# iteration of the training\n",
+ "\n",
+ "x = tf.placeholder(tf.float32, name='x')\n",
+ "y = tf.placeholder(tf.float32, name='y')"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "8hPRkaoxvRyV",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the linear regression model\n",
+ "\n",
+ "# tf.Variable?\n",
+ "# We define the model parameters as tf.Variables\n",
+ "# as they get updated throghout the training.\n",
+ "# And variables denotes something which changes overtime.\n",
+ "\n",
+ "W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ "b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ "\n",
+ "pred_y = (W*x) + b"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "cSw1P8bkv96r",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the loss function\n",
+ "# We are going to use the mean squared loss\n",
+ "loss = tf.reduce_mean(tf.square(y - pred_y))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "5G4uQqjsygNj",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the optimizer\n",
+ "# And specify the which value (i.e. loss) it has to minimize\n",
+ "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "ttI7ZT-ozAm1",
+ "colab_type": "code",
+ "outputId": "e4f2ee17-a8bf-4d4c-8564-c8128dcf5365",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 434
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# So the graph is now built\n",
+ "# Now let's execute the graph using session\n",
+ "# i.e. lets train the model\n",
+ "\n",
+ "# What it is to train a model?\n",
+ "# To update the paramters in the graph (i.e. tf.Variables)\n",
+ "# So that the loss is minimized\n",
+ "\n",
+ "# Okay let's start!\n",
+ "with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.25383937\n",
+ "Loss after epoch 20 is 0.25364405\n",
+ "Loss after epoch 40 is 0.2534488\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.021730803\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xd4VGX6xvHvlBTSgCGF3kIoSagC\nUlRaQMFtP9dVVKwoIGBFBUEWXBQVsQAqIrKuq+iy67KubUVBrDSRmgQIhBZaGiGQhJSZOb8/CIGR\nEkqSk5ncn+vigmTeOXkeIrk957znfS2GYRiIiIhItWE1uwARERHxpHAWERGpZhTOIiIi1YzCWURE\npJpROIuIiFQzCmcREZFqxm52ASdlZh4z9evXrRtETk6BqTVUJl/vD3y/R/Xn3Xy9P/D9Hiu6v4iI\n0HO+dkFnzikpKSQkJPD++++f8VpRURHjx4/nhhtu8Pj89OnTufnmmxk6dCibNm26yJKrnt1uM7uE\nSuXr/YHv96j+vJuv9we+32NV9lduOBcUFDBt2jR69ux51tdnzJhBu3btPD63Zs0a9uzZw6JFi3j2\n2Wd59tlnK6ZaERGRGqDccPb392f+/PlERkae9fVHHnmEhIQEj8+tXLmy7HPR0dHk5uaSl5dXAeWK\niIj4vnLvOdvtduz2cw8LCQnhyJEjHp/LysoiLi6u7GOHw0FmZiYhISHnPE7dukGmXxI53/V/X+Dr\n/YHv96j+vJuv9we+32NV9VclE8IuZPlusycRRESEmj4prTL5en/g+z2qP+/m6/2B7/dY0f1d9oSw\nixUZGUlWVlbZxxkZGURERFTGlxIREfE5lRLOvXv3ZsmSJQAkJSURGRl53kvaIiIickq5l7UTExN5\n4YUX2L9/P3a7nSVLltC/f38aN27MwIEDefDBBzl06BC7du3i9ttv56abbuK3v/0tcXFxDB06FIvF\nwpQpU6qiFxEREZ9gqS77OZt9n+Js9xLmzHmFbdu2cPhwNoWFhTRs2IiwsNpMn/5ihXzNG2/8LZGR\nUVitpy5gvPbaW5d93B9//I4rr+zF0aO5LFgwjyeemOTz94JA97u8nfrzfr7eY1Xec642K4RVRw88\n8AgAX3zxKTt3pjJ27MMV/jVmzpxNUFBQhR7zH/9YSJcu3ahXL5wnnphUoccWEZHKp3C+BOvWreUf\n/3ifgoICxo59hHHjxvL558sAeOqpJ7jhhpto27Yd06c/zbFjx3C5XDz88OO0ahVzQce//voBZxxv\n/fpfyM/PY+/ePezfv48HHxxHz569+fLLz/noo0VYLBaGDr2NkpISkpMTeeyxB5kwYTJPP/0UCxa8\nx+rVq5kxYyZ2u52IiEiefPLPLF26hE2bNnDkSA579+7h1ltv5ze/+UOl/b2JiMiF8ZpwnrriKT5N\n/bhCj/nb6D8wtdczl/Te1NQdfPjhYvz9/c/6+j//+SFXXtmL3/72D+zatZNZs2by6qtvXE65ZGSk\nM3PmbFatWsF///tvOnbsxN/+9jbvvvshxcUlPPvsFJ5//mXefvtNZs6cTW7uqefPp0yZwsyZc4iK\nqs/LL7/A119/icViITV1B2+++Vf27UtjypSJCmcRkdPl52Pfmox9SzL0uwoaRVfJl/WacK5uWrWK\nOWcwA2zevIkjR3JYsuQLAIqKCs867rHHHiy751ynTl2eeeaFcx6zQ4dOwIlH1fLy8ti9exdNmzYn\nICCQgIBAnn/+5bO+7+jRXCwWC1FR9QHo0qUrGzaso3XrtsTHd8BmsxEREUl+vlZxE5EayjCwHjqI\nPWkz9sTN2JISsSduwrYzFcvJqVmDB8O7i6qkHK8J56m9nrnks9zK4Ofnd9bPO53O0tftPPLI48TH\ndzjvccq753zyeAA226kV1AzDwGq1YRjuC6jW4rEQTElJCRaL9azHFBHxeSUl2LanYE/chD0pEXvi\nZuzJm7FmZ3sMc9euQ0nP3jjj2+OMa0/YLTdWWYleE87VmcViobDwxJlxSso2AGJj4/n++2+Jj+/A\nrl07Wb16BUOHDrvk451Ns2bN2bt3DwUFBdhsNsaPf4RXXnkdi8WKy+UqGxcWFobFYuHQoUPUr1+f\nDRvW0aFDJ48xIiK+yHIkpzSATwSxLSkR+7YtWIqLPca5mjWnqEdvnHHxOOM74IyLx924CVgspwZF\nhEIVzUZXOFeAP/zhRkaMuJPmzVvSps2JHbpuvPFmnn12KqNH34vb7ebhhx+7rOOdTa1atRg+fBQP\nPzwagJtvvhWLxULnzl0YPXo4kyZNLRs7bdo0nn56EjabjUaNGjNgwCC++up/l9awiEh143Zj3bP7\nxFlw0slfidj2pXkMMwIDTwVw7InfXbGxGKFhJhV+dnrOuZSez/N+vt6j+vNuvt4fVGGPBQUnJmkl\nnhbCSYlYfzVvxhUZhav0kvTJQHa1jIbzbOZ0PnrOWURExDCwZqSfmJh1+qXp1B1Y3Kfm2xg2G65W\nMRTHlQZxaSAb59jq2BsonEVExHwlJdh2bD9zktZpmygBuEPDKOneA2d8e1wng7hNOwgMNKnwyqFw\nFhGRKmXJPXIigJM2Y0s8cVnavjX5zElaTZtRNLiH5yStps08J2n5KIWziIhUDsPAunfPqXvDiZux\nJydi27vHc1hAAM52caWXo+NPnBHHxmHUrmNS4eZTOIuIyOU7fhzWbiPwx9Wn7hEnJWI9dtRjmDs8\nguK+/T3uDbtaxVzyJC1fpb8NERG5KJaMjFP3hpNKJ2nt2A4uFyfnHxtW64lJWgkDTwviDhhRUabW\n7i0Uzudx8OAB7rhjKG3atAWguLiY2267kz59+l30sf7970UcOXKEa67py/fff8vw4SPPOu7kdo/n\nWoHsdDt37uDll2ecsc1knz5X0r59x7KP69WrxxtvvHbRNf/a8uVL6dcvge3bt523BxHxEU4nttQd\npy5Jl/5uzczwGOYOCcXZtTt+XbtwLLrtiXvEbWOhVi2TCvd+CudyNG3arCz8jh7N5e67b6NHj54E\nBFzazMCYmDbExLQ55+snt3u8kHA+l5CQkArZF/rX3n//Xfr1Syi3BxHxPpajudiTk7CdHsRbt2Ap\n9NwXwNWkKUXXDSl9dvjEGbG7aTOwWomICKXQx5/lrioK54sQFlabevXCyc7O5p135mO3+3H06BH+\n8pfnmTHjWQ4c2I/T6eTee0dxxRXdWLt2DbNnv4TDUY969cJp2LAR69atZfHif/LMMzPOu93jrFlz\n+eST/7B06ZdYLFauvrovt9wyjIyMdCZPnoCfnx+tWrW+4Nr37dvH6NFjWbDgPQCGD7+dZ555gb/+\n9S3CwyPYtm0L6emH+POfn6FNm7YsXPgu3367DIvFyqhRY9m6NZkdO1KYOPFxbrzx5rIeli37mkWL\nFmKz2WjTph0PP/wYCxbMO+v2liJSDRgG1rS9Hkta2hM3Y9u723OYvz/OtrEnJmidXMgjNg6jTl1z\n6q5hvCacg6c+RcCnFbtlZNFv/0D+1AvfTOPgwQMcPZpLZOSJeyZhYWGMHz+JL7/8nHr1wnnyyT9z\n5MgRHnpoFO+++w/mzXuNyZOnERPTmscee5CGDRuVHaugIP+82z1mZmbw7bfLeOONBQDcf/9w+vVL\nYPHiRQwYMIibbrqF99//Gzt2pFz230NxcTEvv/waH3/8EV9++TlBQUF8++0y5s37GwcO7Of99//G\nhAmTWbjwXaZPf5F169aW9lDAW2+9zjvvfEBQUBBPPPFI2Wu/3t5S4SxigsJC7Nu2nLgnXHaPOBHr\n0VyPYe7wcIr79PNcSatVDFzGFTy5PF4TzmbZu3cPY8eOAMDf35+nnnoae+mswtjYOAASEzexceN6\nNm3aAEBRURElJSUcPHiQmJgTZ7edOnWhqKio7Ljlbfe4ZUsS+/al8cADJ+7rFhTkc+jQAXbv3kW/\nfgkAdO7clVWrVpxRc15eXlnNANHRrRg9+tz3hzt27AxAREQUyclJpKRsIzY2HqvVSuPGTZgwYfJZ\n35eWtpfGjZuW7arVufMVpKRsBc7c3lJEKpclM/O0SVonLkvbtqdgOW2DG8NiwRXdiuL+A04EcFw8\nzrj2uKPq14hnh72J14Rz/tRnLuost6Kcfs/51+x2v7Lf77jjHgYOvM7j9ZP7NMOZ2zGWt92j3e5H\nz569eeKJSR6fX7jw3bLtHs/1/rPdcy4u9nyc4XxbUdpsVtzu8pdct1g8+3I6SwgICDjrMUWkgrhc\nZ0zSsiVuxpaR7jHMCArG2aWrxwIezraxEBxsUuFyMazlD5HyxMbG8+OP3wGQk3OYefNeByA8PIK9\ne3djGAbr1//i8Z7Tt3ssKiri4YdHYxhG2XaPbdq0Y926XygsLMQwDF59dSZFRYU0bdqMrVuTAcou\nIV+IkJAQcnIOYxgG2dlZHDiw75xj27Rpx+bNG3E6nRw+nM2TT57YUevXgd2kSTP27dtLQUE+AOvX\nr6NNm9gLrklEzs+Sdwz76lUELniLkHEPUufavoS3bIjjqm6EjbyHoDmv4P/NUvDzo2jQdeQ/+ji5\nC/5O9qr1ZO3cz5HPvyZvxisU3nE3ziu6KZi9iNecOVdn/fsnsG7dz4wadQ8ul4t77jlxSXnEiNE8\n9dR46tdvUHaf+qTytnucM+ctbrrpFsaMuQ+r1co11/QlICCQP/3pFiZPnsD33y8nOjrmgmusXbs2\nXbt2595776BVq5jzzrZu0KAh1147hLFjR2AYBiNHjgGgdes23HffHdx//4NlPYwZ8xDjxj2AxWKl\nQ4dOdOzYibVrV1/U359IjWcYWPel/WqS1iZse3Z7DvPzw9mmXenl6Piy2dJGXYc5dUul0ZaRpXx9\nOzdf7w98v0f1593K+isqwp6ytXRN6ZOXphOx5h7xGO92OE49rnRyklZMa/D3N6mD8tWY72EFHu9c\ndOYsIlJJLNnZZQHMji3U/WU9tu3bsJw258OwWHC1jKa4T7/SR5ZKJ2k1aKhJWjWYwllE5HK5XNh2\n7SwLYlvSibNh28EDHsNsQcE4O3Y+NUErLh5nbLzuBcsZFM4iIhcjLw97clLp40qla0tvScZSUOAx\nzNWwEUUDry3b3KH2NT3JCosEq+bhSvkUziIiZ2MYWA/s97gvbEvchG33LiynTdUx7HZcrduWhfDJ\nbQ8NRz3P40WEgg/fj5WKpXAWESkuxpay7YxFPKw5OR7D3HXrUtL76lMzpePa42rdBkqf7xepKApn\nEalRLIezTwXwyTPilK1YSko8xjlbtKTkqj6lM6VPBLG7YSNN0pIqoXAWEd/kdmPbvfOMR5ZsB/Z7\nDDOCgnB26IgzrsOpIG4XByEhJhUuonAWEV+Qn499S1LZDkv2pM3Yk5OwlK5ed5KrfgOKEgbhOv3Z\n4RYt4bTlZkWqA4WziHgPw8B66GDZveGTZ8W2namek7RsNlyt23jsOeyMa48RHm5i8SIXTuEsItVT\ncTG27SmnTdI68diS9fBhj2Hu2nUo6dn71JlwXDzO1m0hMNCkwkUun8JZRExnyTkMiWup9dPq0kU8\nErFv23LGJC1Xs+YU9bzKY6cld+MmmqQlPkfhLCJVx+3GuntX2aNKJ+8R2/af2CXt5BQsIzDw1HPD\nJx9ZiovDCA0zr3aRKqRwFpHKUVCAfWvyqQlaiZuxJSdhzc/zGOaKjKK4fwL+3a7gaMsT94ldLaPB\nrh9PUnPpv34RuTyGgTUj/cQWh6c9P2xL3YHF7T41zGbDFdOa4th4z0lakZHAiR16irSClgigcBaR\ni1FSgm3H9tOeGy5dSSsry2OYOzSMkit74oyLx3Vyk4c27TRJS+QCKZxF5KwsuUfKVtKylS7gYd+2\nBUtRkcc4V9PmFA3ucdo94njcTZtpkpbIZVA4i9R0hoF1z+7SyVmn1pa2pe31HBYQgLNdbNklaVdc\ne5yxcRhhtU0qXMR3KZxFapLjx09M0jotiG3JSViPHfUY5o6IpLjfgLIzYWd8B1zRrTRJS6SKXNC/\ntJSUFEaPHs1dd93FsGHDPF5bsWIFL7/8MjabjWuuuYYxY8awevVqHnroIWJiYgBo3bo1kydPrvjq\nReScLOnpp+4NJ5dO0tqx3XOSltWKq1UMxQMHnVpbOq49RlSUiZWLSLnhXFBQwLRp0+jZs+dZX3/m\nmWdYsGABUVFRDBs2jGuvvRaA7t27M3v27IqtVkTO5HSeZZJWItbMDI9h7pBQnF27n7g3fHKSVttY\nqFXLpMJF5FzKDWd/f3/mz5/P/Pnzz3gtLS2N2rVr06BBAwD69OnDypUrad26dcVXKiJYjuZiT07C\ndvLecOJm7FuTz5yk1aQpRdcN8Vhb2t20GVitJlUuIhej3HC22+3Yz3GfKTMzE4fDUfaxw+EgLS2N\n1q1bs2PHDkaNGkVubi5jx46ld+/eFVe1iK8zDKx793jcG2ZrEuG7dnkO8/fH2aZd6QSt+LJ7xEad\nuiYVLiIVoVJmdzRv3pyxY8cyePBg0tLSuOOOO/jqq6/w9/c/53vq1g3Cbjd327aIiFBTv35l8/X+\nwEt7LCyEpCTYsAE2bjzx+6ZNkJvrOS48HBISoFMn6NgROnXC0qYNfn5++JlTeYXzyu/fRfD1/sD3\ne6yq/i4rnCMjI8k6bfGB9PR0IiMjiYqKYsiQIQA0bdqU8PBw0tPTadKkyTmPlZNTcDmlXLaIiFAy\nfXh1Il/vD7yjR0tm5hkLeNi2p2BxucrGGBYLruhWOEtnS7tKnx+uFx9DZpbn0pccKQQKq7aJSuIN\n37/L4ev9ge/3WNH9nS/oLyucGzduTF5eHvv27aN+/fosX76cmTNn8sknn5CZmcnw4cPJzMwkOzub\nKM3+lJrE5cKWuuO0zR1OLG1pSz/kMcwdHIKzS1ePBTyc7eIgKOjMY2pRD5Eao9xwTkxM5IUXXmD/\n/v3Y7XaWLFlC//79ady4MQMHDmTq1KmMGzcOgCFDhtCiRQsiIiJ47LHHWLZsGSUlJUydOvW8l7RF\nvJkl7xi2pKQT94aTS+8Rb92C5fhxj3GuRo0punbwaTstxeNu3kKTtETkDBbDMAyziwBMvxSiyzHe\nr9J7NAys+9LOXElr968mafn54WzTrvRydOm+w7FxGHUd5zjwhfH176H6836+3qPXXNYW8VlFRdhT\ntpauKX1yIY9ErEeOeAxzOxwUX923dPGO0pW0YlqDrhSJyGVQOEuNZ8nK8rg3bE9KxLZ9Gxans2yM\nYbHgahlNcZ/+Jx5ZKr1H7K7fQPeCRaTCKZyl5nC5sO3aeSqAT/5+6KDHMCMoGGenLmdO0goONqlw\nEalpFM7ikyx5x7AlJ3uuLb0lGUuB5yN7roaNKBp0Xdma0q749riat9QkLRExlcJZvJthYD2wH3vi\nZtidQtjqtdiSNmPftdNzmN2Oq3XbU2fDpZO1DEc9kwoXETk3hbN4j+JibNu2li3ecfIe8emTtAIA\nd506FF91TdnZsDOuPa7WbSAgwLzaRUQugsJZqiVLdvapAC69NG3bvg1LSYnHOGeLlpSUzpYO7tWd\n7CatcDdspElaIuLVFM5iLrcb265UbCd3WDoZxAcPeAwzatXC2aEjztj2ZZemXbGxGCGnnhMMjgjF\n7cPPWIpIzaFwlqqTn499S1JpCJc+trQlGUtBvscwV/0GFCUMwhV3ahEPV4uWYDN3YxQRkaqicJaK\nZxhYDx089cjSybWld6ZiOW1BOsNuxxXT5tQqWqX3iI3wcBOLFxExn8JZLk9JCbaUbafttJSIPWkT\n1sOHPYa5a9ehpNdVHo8sOVu31SQtEZGzUDjLBbPkHD41QSsp8cTSlilbsRQXe4xzNW9BUc+rPBbx\ncDduoklaIiIXSOEsZ3K7se7eVXYWbC+drGXbv89jmFGr1qkAji29NxwbixEaZlLhIiK+QeFc0xUU\nYN+a7DlTOjkJa36exzBXVH2K+yecujcc3wFXy2hN0hIRqQQK55ri5CStpM0eOy3ZdqZicbtPDbPZ\ncLVuQ3HsryZpRUSYWLyISM2icPZFJSXYtqectorWZtiSSL3MTI9h7rDalFzZE2d8+xOPLZ2cpBUY\naFLhIiICCmevZ8k9UvbMcNlCHtu2nDFJixYtKOrWw+OxJXeTppqkJSJSDSmcvYXbjXXP7lOLdyQn\nnpgxnbbXY5gREICzXVzZxg4nF/IIj27MUa2eJSLiFRTO1dHx42efpJXnGa7u8AiK+/b3nKQV3Qrs\n+raKiHgz/RQ3k2FgzUg/scXh6UGcusNzkpbViqtVDMXx7T3WljaiokwsXkREKovCuao4ndh2bD+1\nklbp0pbWrF9N0goJxdntSs99h9u0g1q1TCpcRESqmsK5EliO5mJPTsKWeGoBD/vWZCxFRR7jXE2a\nUnTd9Z6TtJo2A6vVpMpFRKQ6UDhfDsPAmrbX45K0PSkR297dnsMCAnC2aVf6yFJpEMfGYdSuY07d\nIiJSrSmcL1RhIfZtW07cEz4ZxMlJWI/megxzh4dT3KffqUvSce1xtYoBPz+TChcREW+jcD4LS0bG\naQt4nHhsybY9BYvLVTbGsFpxRbeieEBCWRC74trjjozSs8MiInJZanY4u1zYUndgT9wEu1KovWYt\ntqREbBnpHsPcIaE4r+jmscuSs20sBAWZVLiIiPiyGhPOlmNHsSUllZ4Rl/7akoylsLBsjD/gatyE\nouuGlO2y5IyLx92suSZpiYhIlfHNcM7Px//7bz0uTdv27PYYYvj54WzTDlfpSlohV/Ugq2ELjLoO\nc2oWEREp5ZPhHDruAQIXf1T2sdvhoPjqvqWPLJVO0oppDf7+ZWNCIkIxtLyliIhUAz4ZzsdHjsEZ\n2x5Xu3Y44zvgrt9Ak7RERMRr+GQ4OztfgbPzFWaXISIickk0y0lERKSaUTiLiIhUMwpnERGRakbh\nLCIiUs0onEVERKoZhbOIiEg1o3AWERGpZhTOIiIi1YzCWUREpJpROIuIiFQzFxTOKSkpJCQk8P77\n75/x2ooVK7jxxhu5+eabef3118s+P336dG6++WaGDh3Kpk2bKq5iERERH1fu2toFBQVMmzaNnj17\nnvX1Z555hgULFhAVFcWwYcO49tprOXz4MHv27GHRokWkpqYyceJEFi1aVOHFi4iI+KJyz5z9/f2Z\nP38+kZGRZ7yWlpZG7dq1adCgAVarlT59+rBy5UpWrlxJQkICANHR0eTm5pKXl1fx1YuIiFSyIlcR\nacf2UuwqrrKvWe6Zs91ux24/+7DMzEwcDkfZxw6Hg7S0NHJycoiLi/P4fGZmJiEhIRVQsoiISMUw\nDIO0Y3tJzk5if94+0vMPkV5wiEP5BzmUf4j0goMcLjwMwA3tbuDNfn+rkrqqZMtIwzDKHVO3bhB2\nu60Kqjm3iIhQU79+ZfP1/sD3e1R/3s3X+4Pq3WOJq4QtWVvYcGgD6w+uZ0P6BjYc2sCRwiNnHV87\noDYNQxvSqUEnGoY2ZFj7YVXW32WFc2RkJFlZWWUfp6enExkZiZ+fn8fnMzIyiIiIOO+xcnIKLqeU\nyxYREUpm5jFTa6hMvt4f+H6P6s+7+Xp/UD17LHGVsHDL31m45e9syU6i2H3q0rQFC9F1WtG3cX/i\nwzvQNLQZ9YMbEBkcRVRQfYL9gj2OVdH9nS/oLyucGzduTF5eHvv27aN+/fosX76cmTNnkpOTw5w5\ncxg6dChJSUlERkbqkraIiFQZwzD4YtdnPLNqCqlHduBv9Se2Xhzx4R2Ij+hAfL0OxIbHEeJXPbOp\n3HBOTEzkhRdeYP/+/djtdpYsWUL//v1p3LgxAwcOZOrUqYwbNw6AIUOG0KJFC1q0aEFcXBxDhw7F\nYrEwZcqUSm9EREQEYPXBVfxl5WR+PrQam8XGXXHDGddtAlFBUWaXdsEsxoXcEK4CZl8KqY6XYyqS\nr/cHvt+j+vNuvt4fmN/j9pwUpq2awpe7Pgfg+pa/Y9KVU2hVN6ZCju81l7VFRETMll6Qzow10/lg\ny99xGS6ubNCTP/f8C93qX2l2aZdM4SwiIl7rs9RPePTbsRwpOkJMndY81fNprms+BIvFYnZpl0Xh\nLCIiXie/JJ8//zSR95LfoZa9Fs9d/SJ3xg3HbvWNWPONLkREpMbYnLmRkV/fw44j24mr1543By6g\njaOt2WVVKO1KJSIiXsFtuHljwxyu+3d/dhzZzsiOY/jyxm98LphBZ84iIuIF0vMPMXbZSL7bt5yI\nWpHMGTCX/k0Hml1WpVE4i4hItWUYBl/u/oJHl48luzCbhKaDmNV/LhFB51910tspnEVEpNoxDIOv\n93zJK7+8yC/pawmwBTD9qhkMbz/S62diXwiFs4iIVBsut4vPdv6XV395iaTszQBc1+J6nuw+mXb1\nYk2uruoonEVExHQlrhL+vf2fzF73MjuObMdqsXJDzI082GUcsfXiyj+Aj1E4i4iIKY4W5bLn6G7W\nHFrF3A2vsffYHvysftzW7g4e6PwwLeu0MrtE0yicRUSk0pS4Slh9aCW7cneyJ3c3e47uZs/RXew5\nupucopyycYG2QIa3H8GYTg/ROLSJiRVXDwpnERGpFC63i1s/v5Hv9i33+HyALYCmoc24IqobzWo3\np2XtaH7f6o9EBkWaVGn1o3AWEZFK8fyaZ/hu33KuanQNN7W5heZhLWgW1pyo4PpYLVoD63wUziIi\nUuH+t+tzZq17ieZhLXjnuvepHVDH7JK8iv7XRUREKtTO3FTGLhtJLXst3rluoYL5EujMWUREKkxB\nSQF3/28Yx4qP8tqAecSFx5tdklfSmbOIiFQIwzB47LuH2HI4ibvj7+WmNreYXZLXUjiLiEiFmLt2\nLh+lLOKKqK78pfdzZpfj1RTOIiJy2dYeWsPDXz5MvcB6vD3o7wTYAswuyavpnrOIiJxVev4hFm37\ngHqB4fRo2JOWtVudddOJrONZ3LvkTlyGi3mD3qFRaGMTqvUtCmcREfGQfTyb19a/yl8T3+K483jZ\n5yNqRdKjYS96NOhJjwa9iK0Xj4HByK/u5kD+fqb3n841jfuaV7gPUTiLiAhwYq3ruRtfY97GN8gr\nOUbD4EZM6fUoAKsPrGDlwRV8mvoxn6Z+DECofxhNQ5uRlL2Z65oPYfxV48nOyjezBZ+hcBYRqeHy\nS/JZsHker61/lSNFRwivFcEW3VvnAAAgAElEQVSTVz7F7bF3E2gPBOCe+PswDIM9R3ez6uAKVh1Y\nwaqDK0jK3kzL2tHMGfCmVv2qQApnEZEawDAMCpwF5JfkU1CST37pr/UZa5m17mWyjmdSJ6AOT/WY\nyvD2Iwn2Cz7jGBaLhea1W9C8dguGtr0NgMyCTGr51SLEL6SqW/JpCmcRER90rPgoT/04gWV7vy4L\nZAPjrGOD/UIY13U893ccS1hA7Yv6OhFBERVRrvyKwllExMesT/+FEV/fzZ6ju2kQ3JDoOq0I9gsm\nyB5EsF8IwX7BpR8HEx4Uzp9a30K9WvXMLltOo3AWEfERbsPN3A2v8ezqqbjcLh7qMo4nuk3Ez+Zn\ndmlykRTOIiI+IKMggweWjWR52jIig6J4I2G+HmvyYgpnEREv923aN4xZOoLM4xkMaDqQ2f3f1L1g\nL6dwFhHxUiWuEl5Y8yxz1r+C3Wpnaq9nGdVxjB5p8gEKZxERL7Q7dxf3L72XX9J/pnlYC94a9A6d\nIruYXZZUEIWziIgXMQyDf277kAk/PEZ+SR43xPyJF/u8Qqh/mNmlSQVSOIuIeIkjhTk88f0jfLxj\nMaH+YbyRMJ8bW99sdllSCRTOIiJe4Kf9PzB22Uj25+2je/0evJ7wFs3CmptdllQShbOISDVW7Cpm\nxprpzFn/ClaLlfHdJ/FQl3HYrfrx7cv03RURqaZ25Gzn/qX3sjFzPc3CmjM34W261u9udllSBRTO\nIiLVjNtw87ekBfxlxWQKnAUMbXsb06+aQYh/qNmlSRVROIuIVCNpx/by8PKx/LDvW+oE1GFW/zf4\nfasbzC5LqpjCWUSkGjAMgw+2vMfkn54kr+QYg5pdx0t9ZxMVXN/s0sQECmcREZMdyj/Io8sfYOne\nrwj1D2N2/7nc3OZWLBaL2aWJSS4onKdPn87GjRuxWCxMnDiRDh06lL22dOlS5s6di7+/P9dffz3D\nhg1j9erVPPTQQ8TExADQunVrJk+eXDkdiIh4KcMw+ChlERN/fILcoiP0adyPV/u9TqPQxmaXJiYr\nN5zXrFnDnj17WLRoEampqUycOJFFixYB4Ha7mTZtGv/5z3+oU6cO9913HwkJCQB0796d2bNnV271\nIiJe6mDeASb88Bj/2/UZQfZgXuzzKnfE3q2zZQEuIJxXrlxZFrjR0dHk5uaSl5dHSEgIOTk5hIWF\n4XA4AOjRowcrVqygUaNGlVu1iIiX2ncsjTnrX+GDLe9R5CqiV8OrmNX/DS0oIh7K3bokKyuLunXr\nln3scDjIzMws+3N+fj67d++mpKSE1atXk5WVBcCOHTsYNWoUt9xyCz/99FMllS8i4h125uxk3LcP\ncuXCTryT+Db1gxvwar/XWfz7zxTMcoaLnhBmGEbZny0WC88//zwTJ04kNDSUxo1P3Cdp3rw5Y8eO\nZfDgwaSlpXHHHXfw1Vdf4e/vf87j1q0bhN1uu4QWKk5EhG8/Q+jr/YHv96j+vE9KdgrTf5jO+5ve\nx2W4aF2vNZOunsSt7W/1yVW+fPF7eLqq6q/c/zIiIyPLzoYBMjIyiIg4tYl39+7d+eCDDwB46aWX\naNSoEVFRUQwZMgSApk2bEh4eTnp6Ok2aNDnn18nJKbjkJipCREQomZnHTK2hMvl6f+D7Pao/71Hi\nKmFT1gbmb3qTj3f8G7fhJjYilgc7jeP30Tdgs9rIyT5udpkVzpe+h2dT0f2dL+jLvazdu3dvlixZ\nAkBSUhKRkZGEhISUvX7vvfeSnZ1NQUEBy5cvp2fPnnzyyScsWLAAgMzMTLKzs4mKirrcPkREqqVj\nxUdZvncZz695hj/+97fELGjC4H8PYPH2f9HWEcuCa//O5vs3c0PMn7BZzb1CKN6h3DPnLl26EBcX\nx9ChQ7FYLEyZMoXFixcTGhrKwIEDuemmm7jnnnuwWCyMGDECh8NB//79eeyxx1i2bBklJSVMnTr1\nvJe0RUS8idtw8+WuL/hh/7esPriK5OxE3Ia77PW2jnZ0r9+TQc2vJaHZtVgtVqyWcs+FRMpYjNNv\nIpvI7Eshuhzj/Xy9R/VXPWzIWMeE78exLuMXAAJsAXSOvIIrG/Ske/0r6Vq/O3UDHWe8z1v6uxy+\n3mNVXtb2vdkIIiKV4HBhNtNXTeO95HcwMPi/Vn9kePtRdIzsRIAtwOzyxMconEVEzsNtuFm45e88\ns3IKOUU5tKnblueumclVja4xuzTxYQpnEZFzWJ/+CxN+GMf6jHWE+IXydK/p3Nt+JH42P7NLEx+n\ncBYROY3bcJOUtZm/JS3g/eR3MTC4IeZPTO31DPWDG5hdntQQCmcRqfH2HUvju7TlfLfvG37Y9x3Z\nhdkAtHPE8tzVM+nV6CqTK5SaRuEsIjVOXkke36d9y3f7vuG7tOXszE0te61BcEOGtr2Nfk0G8JuW\nv9clbDGFwllEaoyMggwWbH6Tvya+TW7REQBC/EK5tvlg+jTuR58m/WlVJ0Y7Q4npFM4i4vN2HtnB\nGxteY9G2hRS5igivFc7DXR5jQLNBdIm8QmfHUu0onEXEZ61LX8tr62fx+c5PMDBoFtac0Z0eZGjb\n26hlr2V2eSLnpHAWEZ/iNtx8s/drXl8/m58O/ABAx4jOPND5Ya5v+TutbS1eQeEsIj6h0FnIRymL\neHPja6TkbAOgX5MBjO38MFc1ukb3kcWrKJxFxKtlHc/incT5vJM4n6zjWditdv7UeiijOo2lfXgH\ns8sTuSQKZxHxSttzUnhz4+v8a9uHFLoKqR1Qhwc7P8rw9iNoENLQ7PJELovCWUS8ytbDW3hm5RS+\n2vMlAM3CmjOyw2iGthtGiF9IOe8W8Q4KZxHxCnklebz08wvM2/Q6TreTbvWv5P6ODzC4xfWa5CU+\nR+EsItWaYRh8vvNTnvpxPAfy99M0tBnTr57BoOaDzS5NpNIonEWk2tqdu4uJPzzO0r1f4Wf149Er\nHufBLuMI8gsyuzSRSqVwFpFqp8hVxGvrX2XWLy9R6Crk6sZ9eeHql2hVN8bs0kSqhMJZRKqVVQdW\n8PDyMezMTSUqqD6zez/H71vdoOeUpUZROItIteByu3h57Qxm/DwdgBEd7md890mE+oeZXJlI1VM4\ni4jpMgoyuPXLUSzduZSGwY2YN+gdrmzQw+yyREyjcBYRU/2w7zvuX3ovGQXpDGp2HbMHzMURWM/s\nskRMpXAWEVO43C5eWvsCL619AZvVxsyBM7m91X26tyyCwllETJCef4hRXw/npwM/0CS0KfMG/pXB\n7QeQmXnM7NJEqgWFs4hUmf3H9vHj/u95euVkso5nMrjFb5jV73XqBNY1uzSRakXhLCKVotBZyOas\njaw99DNr09ew9tAaDuYfAMDP6sezV73Ave1H6TK2yFkonEXkkjjdTrKOZ5JRkE5mQQYZBRlkFKRz\nMP8AGzPXszlzE8Xu4rLxEbUiGdziN3St351rmw2mtaONidWLVG8KZxG5YP/b9TkvrX2BA3n7yD6e\njYFx1nF2q534eu3pWr/7iV9R3WkS2lRnySIXSOEsIuVyuV3M+PlZXvllJn5WP5qFNSembhsia0UR\nGRRJZFBU6a8Tf46uE6P1r0Uug8JZRM7rcGE29399L8vTltEsrDl/u+4D4sLjzS5LxKcpnEXknDZn\nbuTuL4ex99geEpoO4o2E+ZpZLVIFrGYXICLV0z+3fcj1iwey99geHus6gfev/6eCWaSK6MxZRDwU\nu4qZsmIiCza/RZh/bd6+9l0GNR9sdlkiNYrCWUTK7MrdyQPLRrHm0CraOWJ5Z/BCWtaONrsskRpH\n4SxSg7kNNxsz1rNk9xd8uft/JGcnAvB/rf7Iy/1eI9gv2OQKRWomhbNIDXPceZwf933Hl7v/x1e7\n/0d6wSEA/K3+DGg6kBti/sSNrW/WM8kiJlI4i9QQW7KTefWXF1my+38UOAsAcAQ6uLnNrVzbfAh9\nm/QjxD/U5CpFBBTOIj5vR852Xvx5Oh/vWIyBQXSdVgxu8RsGNR9Mt6ju2Kw2s0sUkV9ROIv4qF25\nO3lp7Qt8lLIIt+GmQ0QnxnebSEKza3XJWqSaUziL+Ji0Y3t5Ze2LfLj1fVyGi3aOWJ7oPokhLX6j\nUBbxEgpnER+QV5LHmoOr+GLnZ3y49T1K3CXE1GnN492e5Het/g+rResNiXgThbOIF8ovyWfNwVWs\nOPAjP+3/gQ2Z63C6nQC0qN2Sx7pO4IaYP+l+soiXuqBwnj59Ohs3bsRisTBx4kQ6dOhQ9trSpUuZ\nO3cu/v7+XH/99QwbNqzc94jIxdubu5dXVs3hpwM/sD7jl7IwtllsdIrsQu+GV9Or0VVc3agPfjY/\nk6sVkctRbjivWbOGPXv2sGjRIlJTU5k4cSKLFi0CwO12M23aNP7zn/9Qp04d7rvvPhISEti7d+85\n3yMiF2/x9n/xxPePcLToaGkYd6ZXw6vp3egqutfvoUegRHxMueG8cuVKEhISAIiOjiY3N5e8vDxC\nQkLIyckhLCwMh8MBQI8ePVixYgVpaWnnfI+IXLhjxUcZ//04PkpZRLBfMDP7zOL/Yv5IqH+Y2aWJ\nSCUqN5yzsrKIi4sr+9jhcJCZmUlISAgOh4P8/Hx2795No0aNWL16Nd27dz/ve86lbt0g7HZz749F\nRPj22Yev9we+1eOKtBUMWzyMXUd20a1hNz744we0crQyu6xK5Uvfv7Px9f7A93usqv4uekKYYRhl\nf7ZYLDz//PNMnDiR0NBQGjduXO57ziUnp+BiS6lQERGhZGYeM7WGyuTr/YHv9Oh0O3nllxd5ee0M\n3IabR654jMe6PklDh8Mn+jsXX/n+nYuv9we+32NF93e+oC83nCMjI8nKyir7OCMjg4iIiLKPu3fv\nzgcffADASy+9RKNGjSgqKjrve0Tk7PYe3cPopfex5tAqGoU05o2E+fRs2NvsskSkipX78GPv3r1Z\nsmQJAElJSURGRnpcnr733nvJzs6moKCA5cuX07Nnz3LfIyKnGIbBjpztvLFhDv3+2Zs1h1bx++gb\nWH7TTwpmkRqq3DPnLl26EBcXx9ChQ7FYLEyZMoXFixcTGhrKwIEDuemmm7jnnnuwWCyMGDECh8OB\nw+E44z0ickrW8Sy+37ec79KW8/2+b9mftw+AYL8QZvefy81tbtVqXiI1mMW4kBvCVcDs+xS6V+L9\nqnuPqw6uZMmuL/hu33ISszaVfb5uQF2ubtyXPk36MajZdUQF1z/r+6t7f5dL/Xk/X++xWt1zFpHL\nk1+Sz+QfJ/D+lneBE/smX92oD32a9KNP4360j+io5TVFxIPCWaQSbc7axKiv7mH7kRTiwzvwVI8p\n9GjQmyC/ILNLE5FqTOEsUgkMw+CtTW8wbeUUit3FjOw4hqd6TCXAFmB2aSLiBRTOIhUssyCTB78Z\nxbK9XxNeK5w5/d9kQLNBZpclIl5E4SxSgZbvXcbYZSPJPJ5B3yb9mTNgHlFBUWaXJSJeRuEscpmc\nbiepR3bwwZb3mLtxDn5WP6b2epZRHcdoopeIXBKFs8gFMgyDQ/kH2XI4ieTsZLZkJ5GcncT2nG0U\nu4sBaFk7mnkD/0rHyM4mVysi3kzhLFKOzIJMZvw8nU92LCanKMfjtVr2WsTWi6NdvTjah3dgaLth\nhPhpNTwRuTwKZ5FzKHYV8/bmeby09gWOFR+lYXAjejW6+kQYO+KIrRdLs7AW2Kzm7qYmIr5H4Szy\nK4Zh8NWeL5ny00R25qZSN6Auz139InfGDcdu1T8ZEal8+kkjcpqth7cw+ccJfLdvOTaLjXvbj+Tx\nbk9SN9BhdmkiUoMonEWAw4XZzFgznXeT/orLcNGvyQD+0vs52jjaml2aiNRACmep0dIL0nlr4xu8\nk/g2eSXHiK7Tir/0mk5Cs2u1K5SImEbhLDXSnqO7eX39LD7c+j5FriIiakUyvvtE7o6/D3+bv9nl\niUgNp3CWGmXr4S3MXvcy/9n+ES7DRdOw5ozt9BBD295GoD3Q7PJERACFs9QAhmHwS/rPzF7/Cl/u\n+hyAdo5YHujyCH9o9UfNwBaRakc/lcQnGYbBlsPJfLJjMf9N/Q+pR3YAcEVUNx7qMo5Bza/T0poi\nUm0pnMWnpBzexsc7/s0nqf8hJWcbAEH2IH4ffQN3xt9D74ZXa6KXiFR7CmfxehkFGbyf/Dc+2/0x\niRmJAATaArm+5e/4Q6sbSGh2LcF+wSZXKSJy4RTO4rUKnYW8tWkur/4yk7ySY/jb/LmuxfX8Pvr/\nuLb5YEL8Q80uUUTkkiicxesYhsHnOz9l6sqn2Ht0N45AB9OvnMHo3iMoPqb7yCLi/RTO4lU2Z25k\n8k9PsuLAj9itdkZ2HMO4K56gTmBdageGknnsmNkliohcNoWzeIWMggyeXz2NhVv+joHBoGbX8XTv\nZ4muE2N2aSIiFU7hLNWaYRi8vflNnlv9DHklx2jraMfTvabTr+kAs0sTEak0CmeptvKKj/Hw8rF8\nkvofHIEOXuj5MrfH3qVFQ0TE5+mnnFRLO3K2c9eXt5KSs40rG/Tk7UHvEhVc3+yyRESqhKa2SrXz\nWeonDPqoLyk52xjR4X4W/+4zBbOI1Cg6c5Zqw+l28tzqacxZ/wpB9iDeHLiAG2L+ZHZZIiJVTuEs\n1ULW8SxGfn0PP+z7lha1W/LOdQuJrRdndlkiIqZQOEulyi06wqep/8VluAi0BRJoDyTQXosAWwCB\n9loE2gI4XHiYcd8+yP68fVzbfDCvDZhH7YA6ZpcuImIahbNUCsMwWLTtA/6ycjJZx7PKHW/BwpPd\nJ/PQFeO0W5SI1HgKZ6lwydlJjP/+UVYfXEmQPYgnuk2kRe2WFDoLKXQVUugspKj090JXISXuYq5v\n+TuuanSN2aWLiFQLCmepMHnFx5jx83PM3zQXl+FiSIvf8sxVz9M4tInZpYmIeBWFs1w2wzD4eMe/\nmbJiEofyD9I8rAXPXf0iA5oNMrs0ERGvpHCWy7IjZzvjfxjHD/u+JcAWwOPdnuSBzo8QaA80uzQR\nEa+lcJZLctx5nFd/eZHX1s+ixF1CQtNBPHv1DFrUbml2aSIiXk/hLBdt6Z4lTPjhcfYe3U3D4EY8\ne/UMhrT4DRaLxezSRER8gsJZLtj+Y/t46qcJfL7zE+xWO2M6PcS4buMJ8QsxuzQREZ+icJZylbhK\nmL/5TWasmU6BM58rG/RkxjWv0K5erNmliYj4JIWznNeK/T/y5A+Ps+VwEo5AB89d/SI3t71VC4WI\niFQihbOcweV28b9dn/PGhtmsTV8DwLB2d/JUz6k4AuuZXJ2IiO+7oHCePn06GzduxGKxMHHiRDp0\n6FD22sKFC/nkk0+wWq3Ex8czadIkFi9ezKxZs2jatCkAvXr14v7776+cDqTCFJQUsGjbB7y58TV2\n5e4EYFCz63j4isfoWr+7ydWJiNQc5YbzmjVr2LNnD4sWLSI1NZWJEyeyaNEiAPLy8liwYAFfffUV\ndrude+65hw0bNgAwZMgQxo8fX7nVS4XILMjkr4lv8U7ifA4XHsbf6s+wdncyquNYWjvamF2eiEiN\nU244r1y5koSEBACio6PJzc0lLy+PkJAQ/Pz88PPzo6CggKCgII4fP07t2rUrvWipGAfzDvDS2hks\n2raQIlcRdQPq8ugVj3N3+xFEBUWZXZ6ISI1VbjhnZWURF3dqX12Hw0FmZiYhISEEBAQwZswYEhIS\nCAgI4Prrr6dFixasX7+eNWvWMHz4cJxOJ+PHjyc29vwze+vWDcJut11+R5chIiLU1K9f2U72l1ec\nx4s/vciLK17kuPM4Leu25NEej3JXp7sI9g82ucrLU1O+h75K/Xk/X++xqvq76AlhhmGU/TkvL495\n8+bx5ZdfEhISwp133snWrVvp2LEjDoeDvn37sn79esaPH8+nn3563uPm5BRcfPUVKCIilMzMY6bW\nUJkiIkI5lH6ERds+4LnV00gvOERkUBTTr3qRoW1vw2a1UZDrpgDv/TuoCd9D9ee9fL0/8P0eK7q/\n8wV9ueEcGRlJVtap/XgzMjKIiIgAIDU1lSZNmuBwOADo2rUriYmJ3HjjjURHRwPQuXNnDh8+jMvl\nwmYz98y4Jlu6cykPffEIydmJ1LLXYlzX8Yzp/JAWEBERqYbKfVi1d+/eLFmyBICkpCQiIyMJCTnx\nA71Ro0akpqZSWFgIQGJiIs2bN2f+/Pl89tlnAKSkpOBwOBTMJtl2eCu3fnYjA98byJbsJG5ucysr\nb13H+O6TFMwiItVUuWfOXbp0IS4ujqFDh2KxWJgyZQqLFy8mNDSUgQMHMnz4cO644w5sNhudO3em\na9euNG7cmMcff5x//OMfOJ1Onn322aroRU5T6Cxkxs/TmbthDi7DRd/mfXmq21/oENHJ7NJERKQc\nFuP0m8gmMvs+hS/dK1mf/gsPfDOKlJxtNAtrzrTezzOs201kZeWZXVql8qXv4dmoP+/m6/2B7/dY\nre45i/cochXx0s8vMGf9K7gMF8Pbj+CpHk8T7BesHaNERLyIwtlHbM7cyNhlo9hyOImmoc14tf/r\nXNXoGrPLEhGRS6BwrsacbicWLNis555MV+Iq4dV1M3nllxdxup3cGTecKT3/Qoi/bz9rKCLiyxTO\n1YzbcPPT/h9YtO0DPkv9L8edx3EEOqhXK5x6tcIJrxVBvcB6Jz4OrMeHWxeyOWsjjUIa80q/1+jb\npL/ZLYiIyGVSOFcTO4/sYNG2D/jXtkXsy0sDoGlYcxoGNyT7eBaZBRmk5Gw763tvbXs7f+k9nbAA\nLZ0qIuILFM4myi06wsc7FrNo6wdlWzOG+IVya9vbubntrVzZoKfHvslOt5PDhYfJPp5F1vFMso9n\n0Si0Md3qX2lWCyIiUgkUziY4WpTLrHUvM3/TXApdhViw0KdxP25ueytDWvyWIL+gs77PbrUTGRRJ\nZFBkFVcsIiJVSeFchZxuJ+8l/40Za54luzCbRiGNuTv+Xm5sfTMNQxqZXZ6IiFQTCucqYBgGy/Z+\nxdQVT5GSs41gvxAmXTmFER1HU8tey+zyRESkmlE4V7KkrESmrpjEd/uWY7VYuT32bsZ3n6RL0yIi\nck4K50qSUZDB86un8cHW93Abbvo26c/TvabTrt7597UWERFROFeCT1M/5vHvHuZw4WHaOtoxtdcz\n9G860OyyRETESyicK1BO4WGe/OFxFm//F4G2QKb1fo7h7Udit+qvWURELpxSo4Is2/MVj3z7AIfy\nD3JFVFfm9J9Hq7oxZpclIiJeSOF8mfJK8pjy0yTeS34HP6sfE6/8M2M7P6yzZRERuWRKkMuw6sAK\nxn4zir1Hd9POEcdrCfNoH97B7LJERMTLKZwvQdbxLF5ZO4O3N8/DYrHwYOdHebz7kwTYAswuTURE\nfIDC+SIcKczhjQ1zeGvTXAqc+bSo3ZI5/efRvYHWthYRkYqjcL4Ax4qP8tamuczd8BpHi3OJDIpi\ncs+pDIu9S2fLIiJS4WpcOJe4SvgoZRFL935Fw5BGtK7bhpg6rekR1AXDCMBisZSNzS/J56+J83lt\n3SvkFOVQL7AeU3s9y11xw8+5OYWIiMjlqjHhXOQqYtHWD5i97mX2Httz1jF1A+oSU7cNMXVbUy8w\nnA+3vk/m8QxqB9Rh4pV/5t72IwnxD63iykVEpKbx+XAudBaycMu7zFn3Kgfy9xNgC2B4+xHcEz+C\n3KIj7Diyne05KewpSCUpPZlf0n9mzaFVwIm9lcd1Hc+ojmOoHVDH5E5ERKSm8Nlwzi/J5+9J7/D6\nhllkFKQTZA9iVMexjOn0IFHB9cvGda3fHYCIiFAyM49R7Cpmd+4u0o7toXPUFTgC65nVgoiI1FA+\nGc6f7/yUx797iKzjWQT7hfBg50cZ1Wks4bXCy32vv82f1o42tHa0qYJKRUREzuST4fxt2jcUu0p4\ntOsTjOwwmrqBDrNLEhERuWA+Gc4vXPMSL1zzElaL1exSRERELppPhrNCWUREvJlSTEREpJpROIuI\niFQzCmcREZFqRuEsIiJSzSicRUREqhmFs4iISDWjcBYREalmFM4iIiLVjMJZRESkmlE4i4iIVDMK\nZxERkWrGYhiGYXYRIiIicorOnEVERKoZhbOIiEg1o3AWERGpZhTOIiIi1YzCWUREpJpROIuIiFQz\ndrMLqEzTp09n48aNWCwWJk6cSIcOHcpeW7hwIZ988glWq5X4+HgmTZqE0+lk0qRJ7N27F5fLxRNP\nPEHXrl25/fbbKSgoICgoCIDx48cTHx9vVltlLra/xYsXM2vWLJo2bQpAr169uP/++9m6dStTp04F\noE2bNjz99NNmtHOGi+1v7ty5rFixAgC3201WVhZLliyhf//+1K9fH5vNBsDMmTOJiooypadfO1+P\nS5cuZe7cufj7+3P99dczbNiwc77n4MGDPPHEE7hcLiIiInjxxRfx9/c3q60yl9LfjBkz+OWXX3A6\nnYwcOZJBgwYxYcIEkpKSqFOnDgDDhw+nb9++ZrTk4WL7W716NQ899BAxMTEAtG7dmsmTJ/vM9+9f\n//oXn3zySdmYxMRE1q9fX21/hgKkpKQwevRo7rrrrrL/Bk9asWIFL7/8MjabjWuuuYYxY8YAVfRv\n0PBRq1evNkaMGGEYhmHs2LHDuOmmm8peO3bsmNGvXz+jpKTEMAzDuPvuu43169cbH330kTFlyhTD\nMAwjJSXF+OMf/2gYhmEMGzbM2LZtW9U2UI5L6e/f//638fzzz59xrGHDhhkbN240DMMwHn30UePb\nb7+tgg7O71L6O93ixYuN+fPnG4ZhGP369TPy8vKqqPILd74eXS6Xcc011xjZ2dmGy+Uy7rnnHuPg\nwYPnfM+ECROML774wjAMw3jppZeMhQsXVnE3Z7qU/lauXGnce++9hmEYxuHDh40+ffoYhmEY48eP\nN7755psq7+F8LqW/VatWGQ888MAZx/KV79+v3z916lTDMKrnz1DDMIz8/Hxj2LBhxlNPPWW89957\nZ7w+ePBg48CBA4bL5cc5qOUAAAaUSURBVDJuueUWY/v27VX2b9BnL2uvXLmShIQEAKKjo8nNzSUv\nLw8APz8//Pz8KCgowOl0cvz4cWrXrs3vfvc7nnzySQAcDgdHjhwxrf7yXEp/Z1NcXMz+/fvL/o+4\nX79+rFy5smqaOI/L6c/pdPLhhx+e8X/B1c35eszJySEsLAyHw4HVaqVHjx6sWLHinO9ZvXo1AwYM\nALzje3iu/rp168asWbMACAsL4/jx47hcLtN6OJ9L6e9cfOX7d7rXX3+d0aNHV3ndF8Pf35/58+cT\nGRl5xmtpaWnUrl2bBg0aYLVa6dOnDytXrqyyf4M+G85ZWVnUrVu37GOHw0FmZiYAAQEBjBkzhoSE\nBPr160fHjh1p0aIFfn5+BAQEAPDuu+/ym9/8puz9s2fP5rbbbuPPf/4zhYWFVdvMWVxKfwBr1qxh\n+PDh3HnnnSQnJ5f9IzupXr16Zccx06X2B/DVV19x1VVXERgYWPa5KVOmcMsttzBz5kyMarIo3vl6\ndDgc5Ofns3v3bkpKSli9evX/t3d/IU29cRzH3weXMfVQTXOkU8Qu0m7GQAIbagiL8qI/l92syC4C\nLQgqIUivwiwRwT+41CCoMJoRUuFE8iLqRiGIGSJ64wr807xww7BEuxgeXD+nTfhtZ+P7ujsHzsHP\nvj7Pc/Y9j8iPHz8iXvPz50+thZYINYyULyUlRWt9ut1uysvLtdcRT58+xel0cuPGDRYXF2Mf6C+7\nyQcwNTXF1atXuXDhAh8/fgRImvpt+PLlC4cOHeLgwYPaOb3NoQAGgyFsnthsYWEBk8mkHW/kj9UY\nTOp3zpttnpCDwSAul4vBwUEyMjK4ePEiExMTFBUVAaH3mePj43R1dQHgdDo5cuQI+fn5NDQ08OzZ\nM6qrq+OSI5J/yWe1WjGZTJw4cYLPnz9TV1dHT09PxPvoSTT16+/vD3tvfv36dcrKyti3bx81NTV4\nPB5OnToV8ww72ZxRURTu37/PnTt3UFUVi8Wy4zXbndODaPINDw/jdrt5/PgxAGfPnmX//v0UFxfz\n6NEj2tvbqa+vj+nPv5N/yVdQUEBtbS2nT5/G5/PhdDoZGhqKeB89iaZ+breb8+fPa8eJMIfu1v81\nBpP2m3N2dnbYk9z8/Lz2FDc9PU1eXh4mk4nU1FRKSkrwer0AvHz5kvfv39PZ2cmePXsAcDgc2iaq\nyspKJicnY5zmv3aT7/Dhw9omGpvNxuLiIgcOHAhr38/NzW3Z4om13dZveXmZ2dnZsMni3LlzZGZm\nYjAYKC8v10X9YPuMAMeOHeP58+e4XC5UVSU3NzfiNWlpadq3kUSoIWydD+DDhw90dXXR3d2NqqoA\nlJaWUlxcDCTGGISt85nNZqqqqlAUhfz8fLKyspibm0uq+kGoTW+z2bRjPc6hO/k7/0ZdYjUGk3Zx\nttvteDweAMbHx8nOziYjIwOA3NxcpqentQ/S6/VSUFCAz+ejr6+P9vZ2rb29vr7OpUuXWFpaAkK/\ndBs7LeNpN/m6u7t58+YNENqhuLG4FRYWMjY2BoRawmVlZXFIFG43+QAmJiYoLCzU7hMIBKiurubX\nr18AjI6O6qJ+sH1GgCtXruD3+1leXmZkZITS0tKI1xw/flw7nwg1hK3zBQIBHjx4gMvl0nZmA1y7\ndg2fzwckxhiErfMNDAzQ29sLhNqmfr8fs9mcNPWD0MKUnp6utXj1OofuxGKxEAwG+fbtG6urq4yM\njGC322M2BpP6v1I1NzczNjaGoig0NDTw9etXVFXF4XDQ19fHq1evSElJwWazcfv2bVpaWnj79i05\nOTnaPXp7exkeHqanpwej0YjZbObevXsYjcY4JguJNt/s7Cy3bt1ifX2d1dVV7U8ApqamqK+vZ21t\nDavVqm2Ki7do8wF4PB4+ffoU1tZ+8uQJr1+/Zu/evRw9epS7d++iKEq8YoXZLuPQ0BAdHR0oisLl\ny5c5c+bMltcUFRUxPz9PXV0dKysr5OTk0NjYqHV+4inafC9evKCtrS1sD0FTUxMzMzM8fPgQo9FI\nWloajY2NZGZmxjFZSLT5gsEgN2/eZGlpid+/f1NbW0tFRUXS1A9CD8utra1hr8zevXunyznU6/XS\n1NTE9+/fMRgMmM1mKisrsVgsOBwORkdHaW5uBuDkyZNaKz4WYzCpF2chhBAiESVtW1sIIYRIVLI4\nCyGEEDoji7MQQgihM7I4CyGEEDoji7MQQgihM7I4CyGEEDoji7MQQgihM7I4CyGEEDrzB0bC2iht\nJPgIAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jgmH3wwt1src",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Okay, so we are doing good!
\n",
+ "\n",
+ "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
+ "\n",
+ "Or better, do it yourself!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OZ5TY7B_4E_v",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n",
+ " x = tf.placeholder(tf.float32, name='x')\n",
+ " y = tf.placeholder(tf.float32, name='y')\n",
+ " W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ " b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ " pred_y = (W*x) + b\n",
+ " loss = tf.reduce_mean(tf.square(y - pred_y))\n",
+ " optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)\n",
+ " with tf.Session() as sess:\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ "\n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ "\n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ "\n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ "\n",
+ " print ('The final loss is: ', final_loss)\n",
+ "\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()\n",
+ " pass"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "A6MaclhK4rc6",
+ "colab_type": "code",
+ "outputId": "792b2c58-b191-4c89-eaa6-c43a020d7f78",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 555
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# Okay! Now let's tweak!\n",
+ "linear_regression(learning_rate=0.000034, n_epochs=500)"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.19373068\n",
+ "Loss after epoch 50 is 0.19265419\n",
+ "Loss after epoch 100 is 0.19158578\n",
+ "Loss after epoch 150 is 0.19052546\n",
+ "Loss after epoch 200 is 0.1894731\n",
+ "Loss after epoch 250 is 0.18842869\n",
+ "Loss after epoch 300 is 0.1873921\n",
+ "Loss after epoch 350 is 0.18636337\n",
+ "Loss after epoch 400 is 0.18534237\n",
+ "Loss after epoch 450 is 0.18432906\n",
+ "Testing the Model\n",
+ "The final loss is: 0.7989045\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xl8VPW9//H3mSUzCQmYwIzIphAR\narggKffnVayADfdal9ZereJSFKmIohUVWSIatCRSr3Jd0BZbtNyaCiip9VYvaK20LiBaMZZYVFIF\nFSQJhCVkm+X8/kgyJCQhC0m+yczr2YePzNm+8/3MoXnnfL8zcyzbtm0BAIAu5zDdAQAAYhUhDACA\nIYQwAACGEMIAABhCCAMAYAghDACAIa6ufsLi4kOd2n5ycoJKS8s79Tm6G2qOHbFYNzXHhmiv2edL\nanJ91F0Ju1xO013octQcO2KxbmqODbFYsxSFIQwAQE9BCAMAYAghDACAIYQwAACGEMIAABhCCAMA\nYAghDACAIYQwAACGEMIAABhCCAMAYEiXf3c0AABdIWyHVRmsVGWoQlXBKlWEKlQZrFRVsFKVocra\nbUeWK4IVqgpVqq+3ny477QpZltXpfSSEAQCdqi4Mq+oFX/3limCFvPsc2rN3X6NtR8KyNkiDFaoK\nVamy9mf95aODtTpc3e4+TxqSoX7x/TrwVWgaIQwAMSwUDqkiVKGKQIXKg4dVEaxQRaBc5cFyVQTL\nVRGsUHlkuUIVwXKVB+pvqzmmvKltwfJIWHYWl8Mlj9OreJdXXme8ent6y+88UV6XR15nvDy1P72R\nn97I/h6nV15XzT7x9fYd3HtIlwSwRAgD6IHCdljVoWoFwwFVh6sVCAUUOOpxIFSt6nCgZp9QtQLh\nagXCwdr11QrbYVmyZFmWHJYj8tjS0cuOyPoj++rIflbd0pHlxm1YsiLLOrLtqOeXZckhh/qGE1Va\nWl6zrd7zh+xQg/CrC766oGwcjA2Xa9YdVkWgNjCD5R0akE7LqQR3L8W74hXvitcJnuSacHTFy+P0\nyOuKrxd+DcOwX58TFKyy5G1iW/3lmmCtWed1euVy9OwY69m9B9ApbNtWIBxQZbBCFXVzZrVDhBWR\nocIjw3/VtcFWE3iB2sALKBAK1Ftfu67JgGx+fUhBVQWqVF27PRAOKGSHTL9EPY7DcijBVRuQ7gSd\n6OmvBFeC4l0JinfFNwjPeFeCEtw12xIabKvbt+ltboe73fOoPl9Sp99vvjsihIFuLhAKqDJUocpg\nlcr379Ou0r2qCFXUe3NJzba6ObPKUEW9oDx6/q2iyTm5yFxavXk2W3aX1mnJksfpkcvhVpzTLbcj\nTm6HWwlxCUpy9W603u10K84R18T6OMXV/nQ73HI73Ipz1u5Xb73Dcsi2bdX9L2yHGyzb9ZbDdrh2\nnY5art2v7vFR28IKS3Vt2jqyrYXn83hdKq+oql2uOU6yZcmhBHdNQCbUBmL9wIx3xdcErTteCXXb\nXAmKdycozhHXJW80QtsQwkA72batqlBVZHivbg6tbv6s4dxYM/sEy1URKK83dFiuikBFgyvOzrzq\nqz/053V51cfTp5nhv4bzah5X7dCi0yuPy6s4R5zinHE1QehsPvjiIiHZODydjqZv6h6LV0ixWHOs\nIoQRtYLhYO28V705ssjcWF1I1gRk0/vUn1s7rPpvUKkL2I66WmwwVOiKV2JcvwbzaN7anyf0SpKC\nTnlrw68uRL3OI/Nu8a74etuOHFu3rS5gPU4PV0aAYYRwF6q7cgqEqyNv1HBYDjktpxy1jx1WdHx/\nSl2tVaFKVYaqVBWsrPkYQd1HB0LVNY9rt9V/XBWubrR/XVtVoZptYWdQhyoOHzkmVHXk+YJVHX4F\n6XV6I0N+yZ5kDUgcWDv0l9Bw/syd0GgY8Oh5t4QGc2ptGyrkCgmILjERwqFwSJWhSlWHqiK//I/8\nrFJVsCryS7w6VFXvF/qRdXXH1PzCr1ZV3bGRx0farYoESpWqw1WR4GjtZ9YaB7Ozdp2jiXVOuZxO\n2bYV2V53rCWHnI6GxzZc56z5Q0BWzbrabTXrHPXWOSRZCoaDkTnEBqEYqqydizwSpMfz+bzWqvto\ngtfpiQyhnuA5QXFOjzy1/9WE3ZF5skjwRYKzJkiPDsVIcLprtkfLH0cAupceHcJfHfpS8/56h/ZV\n7ouEZcCuVkWgskFYdtU7KZ2WM/LLP87pkcflVS93L3lcXnmccfI4vYqrnQ+Tat5sEbJDCtthhWUr\nHA4prLBC4VDtGzhqH8tuYt2RbZKtYCig6tp1tsK1bdf+bLCu9vns8HHXWzck6nF65HV6lexJjixH\n/nMdCcmaoPREXoea42sDtN7juteq/v41w7LeyGs7qH8/le6tOO4aAMCkHh3CReV79M6utxUIVdde\n/cQpPi5eXmfjK6K6X97e2p/1H3tcHnkcnkZh6XV6a/etexxXs4+j9pj6gev0GPu8WnuGKOu/k7N+\nMIdrH9essxusczviIqF4PB9F6Ag9/bOBACD18BBOP3Gc/vmTrxuEAXNmrVP/CwVcPfufAQD0WD1+\noot3dwIAeqpWXQLl5OQoPz9flmUpMzNTo0ePjmzLzc3VSy+9JIfDoVGjRunuu+/utM4CABBNWrwS\n3rx5s3bs2KHVq1crOztb2dnZkW1lZWVasWKFcnNz9dxzz6mwsFAffvhhp3YYAIBo0WIIb9y4URkZ\nGZKk1NRUHThwQGVlZZIkt9stt9ut8vJyBYNBVVRUqE+fPp3bYwAAokSLIVxSUqLk5OTIckpKioqL\niyVJHo9Hs2bNUkZGhiZNmqQxY8Zo6NChnddbAACiSJvfFmvbR76mr6ysTMuXL9e6deuUmJioa6+9\nVtu2bdPIkSObPT45OUEuV9PfEdtRfL6kTm2/O6Lm2BGLdVNzbIjFmlsMYb/fr5KSkshyUVGRfD6f\nJKmwsFCDBw9WSkqKJGncuHHaunXrMUO4tLT8ePt8TLH4ESVqjh2xWDc1x4Zor7m5PzBaHI4eP368\n1q9fL0kqKCiQ3+9XYmKiJGngwIEqLCxUZWWlJGnr1q065ZRTOqjLAABEtxavhNPT05WWlqYpU6bI\nsixlZWUpLy9PSUlJmjx5sqZPn66pU6fK6XRq7NixGjduXFf0GwCAHs+y60/ydoHOHm6I9iGNplBz\n7IjFuqk5NkR7ze0ejgYAAJ2DEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQB\nADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhh\nAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBC\nGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCE\nEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAM\nIYQBADCEEAYAwBBCGAAAQwhhAAAMcbVmp5ycHOXn58uyLGVmZmr06NGRbbt379Ydd9yhQCCg008/\nXffff3+ndRYAgGjS4pXw5s2btWPHDq1evVrZ2dnKzs5usH3JkiW6/vrr9cILL8jpdGrXrl2d1lkA\nAKJJiyG8ceNGZWRkSJJSU1N14MABlZWVSZLC4bD+9re/6bzzzpMkZWVlacCAAZ3YXQAAokeLIVxS\nUqLk5OTIckpKioqLiyVJ+/btU69evfTAAw/oyiuv1MMPP9x5PQUAIMq0ak64Ptu2Gzzes2ePpk6d\nqoEDB2rGjBnasGGDJk6c2OzxyckJcrmc7epsa/l8SZ3afndEzbEjFuum5tgQizW3GMJ+v18lJSWR\n5aKiIvl8PklScnKyBgwYoCFDhkiSzjrrLH322WfHDOHS0vLj7PKx+XxJKi4+1KnP0d1Qc+yIxbqp\nOTZEe83N/YHR4nD0+PHjtX79eklSQUGB/H6/EhMTJUkul0uDBw/WF198Edk+dOjQDuoyAADRrcUr\n4fT0dKWlpWnKlCmyLEtZWVnKy8tTUlKSJk+erMzMTM2fP1+2beu0006LvEkLAAAcW6vmhOfMmdNg\neeTIkZHHJ598sp577rmO7RUAADGAb8wCAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAA\nDCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgA\nAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAG\nAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQl+kOAAC61u7duzR1\n6hSNGDFSkhQIBDRs2KmaM2e+nE5nm9q68MLv6uWXX2+w7pZbZqiyslJerzey7r77ctS3b7/j6veH\nH36gk08+RcnJKZo//w4tWbL0uNrrDghhAIhBQ4acrGXLnoosZ2cv0muvrdP551/YIe1nZt6rYcNO\n7ZC26rz88ku68sprlJycEhUBLBHCAABJp58+Sl999aUkae3aNfrTn9bJshz6zncm6sorr1FR0R79\n7Gf3SpKCwaAWLrxPAwcOatNzXHbZxfqf/1mthIQELVv2iIYNS5UkffTRhyovP6Tt2wt11VU/1kUX\nXaL33tuk5cuflMPhUEbGv2vo0GF6880N+vzzf2rx4gc1ffrVevnl11VYuF1Ll/5clmUpIaGXFi5c\npO3bP1Ne3hpZlkM7dnyuiRO/q+uvn9GxL1gHIYQBwKBF7yzU/xa+2GCdw2EpHLbb3ebFqZdo0dmL\nW71/MBjUm2/+RZdccql27fpaGza8riefXCFJuumm6Zo0KUOlpXs1bdoNSk8fpz/+8Q/Ky3tet956\ne7v7WF9h4XatXfu8tmz5WFlZmbrwwh/o4Yd/rl/84mn17t1bCxbcqR/84D916qmn6Y475qp///6R\nYx999CHdfPNtSksbpd/97rd6/vlVGjv22/r44wL97ndrFQ6H9aMfXUwIAwC6j507d+iWW2qCqbBw\nu66+eqrOPXeiXn/9VX311Ze69dYbJUnl5Yf1zTe7dNJJA/TIIw9pxYrlOnTooEaM+NYx28/Jub/B\nnPCjj/6i2X1HjRotp9Mpn8+vw4fLtH9/qeLi4pScnCxJevDBR5o99osvPlda2ihJUnr6OD3zzFMa\nO/bbGjFiZIPn764IYQAwaNHZixtdtfp8SSouPtSpz1t/TnjhwrkaPPhkSZLL5dZZZ43X3Ll3N9g/\nJ+c+nXnmv+mSSy7TG2/8Se+889Yx229qTtiyrMjjYDAYeVz/zWC2bcvhcLRrJCAYDMjhcDRqszvj\nI0oAEONuvvk2/fKXj6uyslIjRnxLH3zwN1VWVsq2bT3yyEOqqqrU/v37NXDgINm2rbfe+osCgUCb\nnychoZf27i1RKBRSQcHfm92vT58TFA6HVFxcJNu2NXfubB06dEgOh0OhUKjBvkOHpmrr1o8kSVu2\nfNDiFXp3w5UwAMS4AQMGauLE72rlyhW68cZZuvzyKzVr1g1yOBw699yJ8ni8+sEP/lP//d//pf79\nB+iyy67Qgw9ma/PmTW16nksvvVzz5t2uIUNO1tChw4657513ztfChfMkSeedl6GkpCSdcUa6Fi6c\npwceeDiy3+zZcyJvzEpKSlJmZpY++WRb218EQyzbtts/+98OnT3E0hXDON0NNceOWKybmmNDtNfs\n8yU1uZ7haAAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhM8JA0CMOfpWhtXV1br66ms1YcKk\nNre1du1q7d+/X+eeO1F//esGTZ9+Y5P7vfXWX3TmmWfL7Xa32OY//7ldS5c+2OAuT5I0YcKZ+pd/\nGRNZ7tu3r+6774E29/lob7zxJ02alKHPPvvkmDV0BkIYAGJQ/a+tPHjwgKZNu1r/9m9nyeNp3/ct\nDx8+QsOHj2h2+6pVuUpP/9dWhXBzEhMTGwVzR3j22ZWaNCmjxRo6AyEMADGud+8+6tu3n/bu3atn\nnvmVXC63Dh7cr/vvX6IHH8zWrl1fKxgM6ic/malvf/tf9f77m/XYYw8rJaWv+vbtpwEDBuqDD95X\nXt4aLV78oNate1kvvLBalmVpypSrFQgE9PHHWzVnzk/16KO/0Esv/b7RrRK/+eYb3XzzLXK73Tr1\n1NNa3ffdu3dp4cJ5WrHit5Kk6dN/rMWLf66nn35K/fr59Mkn/9CePd/o3nsXa8SIkcrNXakNG16X\nZTk0c+Yt2rbtY23f/qkyM+/SZZddEanh9ddf0+rVuXI6nRox4luaPXuOVqxYrsOHy7Rz5w59/fVX\n+ulP79RZZ40/rteeEAYAg3otWijP/za8laEcllKO41aGVRdfosOLWn8rw927d+ngwQPy+0+UJPXu\n3Vvz5t2tdeteVt++/bRgwb3av3+/brttplauXKXly5fpnnt+puHDT9OcOT/VgAEDI22Vlx/Wb37z\na61c+ZyqqwPKzs7SkiVL9etf/1IPPfSYiouLmrxV4v/93+/13e/+uy6//Eo9++xvtH37p+2uv051\ndbWWLl2mF198QevWvayEhARt2PC6li//jXbt+lrPPvsbzZ9/j3JzVyon57/0wQfv19ZQrqeeekLP\nPPM7JSQkaO7c2yPbior26KGHHtOmTe/oD39YSwgDANqu/q0M4+LitHDhfXK5aiLh9NPTJElbt36k\n/Pwt+uijDyVJVVVVCgQC2r17t4YPr7laPeOMdFVVVUXa/eKLzzVkyCnyeLzyeLxasmRpg+f9xz8K\nmrxVYmFhoa6+epokaezYcdq06Z1GfS4rK4v0WZJSU0/VlCnXNFvjmDFjJUk+34n6+OMCffrpJzr9\n9FFyOBwaNGiw5s+/p8njvvxypwYNGqKEhITa/nxbn35a833Uo0efIUny+/0qKytr9rlbq1UhnJOT\no/z8fFmWpczMTI0ePbrRPg8//LA+/PBD/fa3vz3uTgFArDi8aHGjq1afL0n7uvBWhkdzudyRn1On\nXq/Jk89vsL3udoFSza0HG25zyrbDzT5vc7dKfP75XFmWo7bNpo9vak74m292N1g+1i0Snc7W3SLR\nshrWFQwG5PF4mmzzeLX4EaXNmzdrx44dWr16tbKzs5Wdnd1on+3bt+u999477s4AALqP008fpbfe\n+oskqbR0n5Yvf0KS1K+fTzt3fiHbtrVly98aHHPyyado584dKi8vV1VVlWbPvlm2bcuyam5D2Nyt\nEocOHapt2z6WpMjQb2skJPRSaek+2batvXtLtGvXV83uO2LEt/T3v+crGAxq3769WrBgjiQ1CubB\ng0/WV1/tVHn5YUl1t0g8vdV9aosWr4Q3btyojIwMSVJqaqoOHDigsrIyJSYmRvZZsmSJbr/9di1b\ntqxTOgkA6HrnnZehDz54TzNnXq9QKKTrr68ZCp4x42YtXDhP/fufFJlHrhMfH6/p02dq9uybJUlX\nXHGVLMvS2LHpuvnm6Xr88aeavFXi1KlTNWvWrfrrX99QaurwVvexd+/eGjfu/+knP5mqU08dfsx3\nN5900gD9x39coFtumSHbtnXjjbMkSaedNkI33DBVN93000gNs2bdpjvvvFWW5dDo0WdozJgz9P77\n77bp9WuNFm9leM8992jChAmRIL7qqquUnZ2toUOHSpLy8vJUUlKiCy64QAsWLGhxODoYDMnlch5z\nHwAAYkGb35hVP7P379+vvLw8PfPMM9qzZ0+rji8tLW/rU7ZJtN+TsinUHDtisW5qjg3RXnO77yfs\n9/tVUlISWS4qKpLP55Mkbdq0Sfv27dPVV1+tW265RQUFBcrJyemgLgMAEN1aDOHx48dr/fr1kqSC\nggL5/f7IfPD555+vV155RWvWrNGyZcuUlpamzMzMzu0xAABRosXh6PT0dKWlpWnKlCmyLEtZWVnK\ny8tTUlKSJk+e3BV9BAAgKrVqTnjOnDkNlkeOHNlon0GDBvEZYQAA2oBbGQIAYAghDACAIYQwAACG\nEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACA\nIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMA\nYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIA\nABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQw\nAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABjias1OOTk5\nys/Pl2VZyszM1OjRoyPbNm3apKVLl8rhcGjo0KHKzs6Ww0G2AwDQkhbTcvPmzdqxY4dWr16t7Oxs\nZWdnN9h+77336rHHHtOqVat0+PBhvfnmm53WWQAAokmLIbxx40ZlZGRIklJTU3XgwAGVlZVFtufl\n5al///6SpJSUFJWWlnZSVwEAiC4tDkeXlJQoLS0tspySkqLi4mIlJiZKUuRnUVGR3n77bd12223H\nbC85OUEul/N4+twiny+pU9vvjqg5dsRi3dQcG2Kx5lbNCddn23ajdXv37tXMmTOVlZWl5OTkYx5f\nWlre1qdsE58vScXFhzr1Obobao4dsVg3NceGaK+5uT8wWhyO9vv9KikpiSwXFRXJ5/NFlsvKynTD\nDTdo9uzZOuecczqgqwAAxIYWQ3j8+PFav369JKmgoEB+vz8yBC1JS5Ys0bXXXqtzzz2383oJAEAU\nanE4Oj09XWlpaZoyZYosy1JWVpby8vKUlJSkc845Ry+++KJ27NihF154QZJ00UUX6Yorruj0jgMA\n0NO1ak54zpw5DZZHjhwZebx169aO7REAADGCb9UAAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgA\nAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAG\nAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGE\nAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMI\nYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQ\nQhgAAEMIYQAADCGEAQAwhBAGAMAQl+kOHA9rzx71yrlPjrKyIys9LvWuCnbME9h2x7TT2e3Wr7mn\n9Pl4227Vee5mfe6IduNc6l3dzn/fPfXfxvHUfAxWd3494lzq01TN3bnPzbbdyv3inOpTHWpDu53X\n53D//jr0yBOS291pz1GnR4ew8/N/yrvmOVmhhifOY6g/JlFz7IjFumOx5jjTHTCgu9Qc9vllHS6T\nfUJypz+XZdud+SdQY8XFhzq0PevQQamqOrLcr1+iSkrKjnFEW5/A6ri2GrTbcU3165ekkpJ6r2un\n9bmT2m1H241q7qB228TA69zqupthd+Q/vPo68XX2+Xt3+O+NiG76/xWfL6n5mrtpn4+37WPWfBzt\ntovDUfNfB/L5kppc36or4ZycHOXn58uyLGVmZmr06NGRbe+8846WLl0qp9Opc889V7NmzeqYHreS\nndRbql+bL0m2vF3aB+P6JskOd5e/IbvICUmyA07Tveh6SUmyK013ooslJEgJbRimjAZer+QNmO5F\n13K7u2T4t7tpMeo3b96sHTt2aPXq1crOzlZ2dnaD7YsXL9bjjz+u5557Tm+//ba2b9/eaZ0FACCa\ntBjCGzduVEZGhiQpNTVVBw4cUFntG6G+/PJL9enTRyeddJIcDocmTJigjRs3dm6PAQCIEi2GcElJ\niZKTj0xOp6SkqLi4WJJUXFyslJSUJrcBAIBja/O7o4/3fVzJyQlyuTp3Lq+5CfBoRs2xIxbrpubY\nEIs1txjCfr9fJSUlkeWioiL5fL4mt+3Zs0d+v/+Y7ZWWlre3r63SrnfY9XDUHDtisW5qjg3RXnNz\nf2C0OBw9fvx4rV+/XpJUUFAgv9+vxMRESdKgQYNUVlamr776SsFgUG+88YbGjx/fgd0GACB6tXgl\nnJ6errS0NE2ZMkWWZSkrK0t5eXlKSkrS5MmTtWjRIt15552SpAsuuEBDhw7t9E4DABANevyXdRwt\n2oc0mkLNsSMW66bm2BDtNbd7OBoAAHQOQhgAAEMIYQAADOnyOWEAAFCDK2EAAAwhhAEAMIQQBgDA\nEEIYAABDCGEAAAwhhAEAMKTNtzI0IScnR/n5+bIsS5mZmRo9enRkW25url566SU5HA6NGjVKd999\nt4LBoO6++27t3LlToVBIc+fO1bhx47Rt2zYtWrRIkjRixAjdd999hipqWUfV/OMf/1jl5eVKSEiQ\nJM2bN0+jRo0yVdYxtbXmvXv3at68eaqqqlIgENCCBQs0ZsyYqD7PzdXck86z1Pa665SUlOh73/ue\nli1bpjPPPDOqz3Wdo2vuSee6rTXn5eXp0Ucf1ZAhQyRJZ599tm666aYedZ7bzO7m3n33XXvGjBm2\nbdv29u3b7csvvzyy7dChQ/akSZPsQCBg27ZtT5s2zd6yZYv9wgsv2FlZWbZt2/ann35qX3rppbZt\n2/Y111xj5+fn27Zt23fccYe9YcOGLqyk9Tq65k8++aRrC2iH9tT89NNP2y+99FLk+GnTptm2Hd3n\n+Vg194TzbNvtq7vOXXfdZf/whz+0N23aZNt2dJ/rOk3V3BPOdXtqXrt2rb1kyZJGbfWU89we3X44\neuPGjcrIyJAkpaam6sCBAyorK5Mkud1uud1ulZeXKxgMqqKiQn369NH3v/99LViwQJKUkpKi/fv3\nq7q6Wl9//XXkL7FJkyZp48ZIjxlCAAAEAUlEQVSNZopqQUfV3JO0p+Zp06bp4osvliTt3r1bJ554\nYtSf56Zq7mnaU3fdcb169dJpp50mSVF/ruuOq19zT9Lemo/Wk85ze3T74eiSkhKlpaVFllNSUlRc\nXKzExER5PB7NmjVLGRkZ8ng8uvDCCxvdSnHlypW66KKLVFpaqt69e0fW9+3bV8XFxV1WR1t0VM11\nHnvsMZWWlio1NVWZmZnyer1dVktrtbfm4uJizZw5U4cPH9bKlStj4jwfXXOdnnCepfbVXV1drSee\neEJPPvmkcnJyJCnqz3VTNdfpCee6PTVv2bJFmzdv1vTp0xUMBjVv3jz17du3x5zn9uj2V8JHs+t9\ny2ZZWZmWL1+udevW6fXXX1d+fr62bdsW2Z6bm6uCggLNmjXrmO10d8dT89SpUzV37lzl5ubKsizl\n5uZ2ef/bo7U1+3w+rV27VgsWLIiMBDTXTnd3PDX31PMsta7up556Sj/60Y8a/DI+Vjvd3fHU3FPP\ndWtqHjNmjG699VatWLFCs2fP1rx5847ZTjTo9lfCfr9fJSUlkeWioiL5fD5JUmFhoQYPHqyUlBRJ\n0rhx47R161aNHDlSzz//vP785z/rySeflNvtbjREu2fPHvn9/q4tppU6qmZJmjx5cqSd8847T6+8\n8koXVtJ67an54MGDGjFihPr06aMJEyZo7ty5UX+em6pZ6jnnWWpf3W+99ZbC4bByc3O1c+dOffTR\nR1q6dGlUn+uman700Ud7zLluT82XXXaZUlNTJUljx47Vvn37lJyc3GPOc3t0+yvh8ePHa/369ZKk\ngoIC+f1+JSYmSpIGDhyowsJCVVZWSpK2bt2qU045RV9++aVWrVqlZcuWyePxSKqZgxg2bJjef/99\nSdKrr76q73znOwYqallH1Wzbtq677jodPHhQkvTuu+9q+PDhBipqWXtqfvXVV/X73/9ekvTJJ5/o\npJNOivrz3FTNPek8S+2re9WqVVqzZo3WrFmjiRMnKisrSyNHjozqc91UzaeeemqPOdftqflXv/qV\n/vjHP0qSPv30U6WkpCguLq7HnOf26PZXwunp6UpLS9OUKVNkWZaysrKUl5enpKQkTZ48WdOnT9fU\nqVPldDo1duxYjRs3LvIX8owZMyLtrFixQpmZmbr33nsVDoc1ZswYnX322QYra15H1nz55Zfruuuu\nU3x8vE488UTdeuutBitrXntqHjZsmObPn6/XXntN1dXVkY8wRPN5bqpmy7J6zHmW2ld3c6L5XDel\nJ53r9tQ8aNAg3XXXXVq1apWCwaCys7Ml9Zzz3B7cyhAAAEO6/XA0AADRihAGAMAQQhgAAEMIYQAA\nDCGEAQAwhBAGAMAQQhgAAEMIYQAADPn/UcnFMvxhd3sAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "peoHmV2M40uU",
+ "colab_type": "code",
+ "outputId": "aa2dfc59-6aa2-4bad-8fc7-4c6872854f9b",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 729
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0000006, n_epochs=1000)"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.19373068\n",
+ "Loss after epoch 50 is 0.19371162\n",
+ "Loss after epoch 100 is 0.19369255\n",
+ "Loss after epoch 150 is 0.19367348\n",
+ "Loss after epoch 200 is 0.19365443\n",
+ "Loss after epoch 250 is 0.19363537\n",
+ "Loss after epoch 300 is 0.19361633\n",
+ "Loss after epoch 350 is 0.19359727\n",
+ "Loss after epoch 400 is 0.19357823\n",
+ "Loss after epoch 450 is 0.19355917\n",
+ "Loss after epoch 500 is 0.19354014\n",
+ "Loss after epoch 550 is 0.19352108\n",
+ "Loss after epoch 600 is 0.19350204\n",
+ "Loss after epoch 650 is 0.19348301\n",
+ "Loss after epoch 700 is 0.19346401\n",
+ "Loss after epoch 750 is 0.19344495\n",
+ "Loss after epoch 800 is 0.19342592\n",
+ "Loss after epoch 850 is 0.19340691\n",
+ "Loss after epoch 900 is 0.19338787\n",
+ "Loss after epoch 950 is 0.19336885\n",
+ "Testing the Model\n",
+ "The final loss is: 0.82940775\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xt41NWdx/HPb67JJAGTMJG7hoCw\nhgVJ2bpKq2DDXqpu7ZYKXVosUhFFKypyidSgJZG1SouiXexSy7YpoJJ23doFWytbL0FqUVziCiWt\nAQVJAiEQkkkyM7/9I8mQkEAuJDlJ5v16Hp6Z3/185/Dkk985kxnLtm1bAACgxzlMNwAAgGhFCAMA\nYAghDACAIYQwAACGEMIAABhCCAMAYIirpy9YWnqqW8+fmOhTeXlVt16jt6Hm6BGNdVNzdOjvNfv9\nCa2u73d3wi6X03QTehw1R49orJuao0M01iz1wxAGAKCvIIQBADCEEAYAwBBCGAAAQwhhAAAMIYQB\nADCEEAYAwBBCGAAAQwhhAAAMIYQBADCkxz87GgCAnhAMBxUIVisQqlFNMKBAqFqBYI1qQgEFggEF\nGh5rQgHVhGpUHaxWTSig5JhBmnHZTFmW1e1tJIQBAN3Gtm0FQgHVBJsGXc2ZcAwFFAhWy1vq0NHj\nx1XTEJjVTY5p3DfQEJJnnjdsaxKsTbeH7FCn2z1tZKYGxQ7qwleidYQwAESpYDio6mCVquqqVBWs\nUnWwWtWNj3X1j2fWV0f2rW6yb1WTfZseX1V3WtXBagVCgW6tIcYZI68rRl6nVzGuWMV74hXjiq1f\ndsYoxhUjr7N+e6wrVl6XVzHOxscz22MbjvE6YzRiwMgeCWCJEAbQR4TtsGpDtQqG61QbrlVdOKi6\nUK3qwnWqC9WvC4brVBuqi+zTuFwXPrNfXbh+OWyHZclqGHK05LAckWWrleWzHx2W48y6JstSK9st\nS5bU7Jznu2ZiVZwqTlTLimyvP2vIDjcLwOq6JkF4Voi2CMu6pvvUP68L13VZ/zgsh3yuOMW6YhXr\n9uniuMGKdcUqxhUbCcrYSGDWh1+M80x4Dho4UMGA1bAcEzkmxhmrGJe31WM8To8cVt9+axMhDCAi\nFA41mydrPp92Zh6tpsV8WpNwbBJ0daFgswA8E4y1CoaDbQZlXbjh+FDdBQ0tRjuPw6NYt0+xrljF\nueM0KNYfCUufK7b+ucvX/NHtk89V/69xObbJvr6z9vU4PBc0h+r3J3T79833RoQw0MvYtq3acG2r\n82KxAaeOlB1rCMgaBULVqml4bPmGk/o5s5pQQNWRUA00W256bCBUrWA42KO1Oi2nPE6PXA63PA53\n/aPTozh3nNyOi+R2ehTr8coKO+V2uOV2uuVxNOzvbNi/ybLb4YnsV//okdvhktvhkcfZsK3hn2U5\nJNmybVt2w2NY4ebLdli27Ei/NC6fvb1x2W5ctiNrFbabL9t2+PzXVFi+WI9OVwVk22p2DYcc8rl9\nTQIzVj53XItAbBqUMa5YuRz8qO+t6BmgA2zbPufcV9VZy2cPC1a1OqfWcv/qYHXkB3938Dg8Z+bM\nXDFK9CbJGxfTZH7MG9keG9kvVjHOxiHB+vm02IZ5tfr5Nk+zADwTjB65HK76ZWd90LqbhGF7hhKj\n8Q4pGmuOVoQw+oVQOBS566sN1TYMmdbf3Z39ppOWc2XN59TOhGLL/auCVV3abp/LF7mzSY4dpFiX\nLzLvFdMwH9YYdLGuGCUmDFC41hFZbv6Gk6bzaC2DtHFOra/PoQH9CSHcDWzbVl24TrWhGgVCNaoN\n1TQERP3z2lCtLMuSQw45LIccDmfkudNy1q+zLDkiz8+styLPrch6X61DgWCg2b498fdtjYLhYCT0\n6msORGptHCJtnDdsHAJtDMzG16WmcSg18nrVD7c2vnaBhnBtHFKts2sVqAtE/sShO4ZRWwtIn7v5\nvJnPFadYd2xkONDn8jUbDmxtuLDxnDHOmA73E3dIQP/Sb0K4MfhO1ZxSWXVZi+Br/rw2Ms9WG66N\nhEVtqEY14ZpImDSGRvPnta2et6YhXBtDqDdoHuqOs0Ld0fBOTIecTX4JqP+FwGq+riHUg+G6MyHZ\nOE8ZCihsh3uklhhnrLxOj7yuGPk8sYp3Jcjj9EaGVT1OT/3dntMrT8M/n9t3VgDGdVtAAkBH9ekQ\n3lv2v5r98ldVHjjeo8FXHwj1P/Q9DX+LdpH3oobnZwLgzHNPZH+v0yu30yOp/g0XITsk2w5Hnocb\n3uwRtkMNj43rw7LtsEIN65ru4/I4VB2oabI+rLDCCoUbjmt8rvpzh8Ih2Wp+7si1wkHV2WGFgqGz\n2mHL43TL46gf3kz0JkYC0OuKkdfhOfO3eo21NgyPnh2OjfOOja9R43GNQ6aR564zy2e/sYQ7QgD9\nQZ8OYZ8rViMHXKLBcYPldcbI4/QqIdYnK+SKBF7jP8/Zz11eeR0NAemqP9bj8ER++Huc9dvrg8Ab\nCZLWAsE0AgkA+qbelSYdNOqi0fqvL29vto5AAgD0FbxNEgAAQ9p1J5ybm6s9e/bIsixlZWVpwoQJ\nkW15eXl66aWX5HA4NH78eD344IPd1lgAAPqTNu+Ed+3apeLiYm3ZskU5OTnKycmJbKusrNSGDRuU\nl5enTZs2qaioSO+99163NhgAgP6izRAuKChQZmamJCktLU0VFRWqrKyUJLndbrndblVVVSkYDKq6\nuloDBw7s3hYDANBPtDkcXVZWpvT09MhyUlKSSktLFR8fL6/Xq4ULFyozM1Ner1fXX3+9UlNTz3u+\nxESfXC7nhbf8PPz+hG49f29EzdEjGuum5ugQjTV3+N3Rtn3mM20rKyu1fv16bdu2TfHx8brlllv0\n4Ycfaty4cec8vry8az/272zR+O5oao4e0Vg3NUeH/l7zuX7BaHM4OiUlRWVlZZHlkpIS+f1+SVJR\nUZFGjBihpKQkeTweTZ48WXv37u2iJgMA0L+1GcJTpkzR9u31f4tbWFiolJQUxcfHS5KGDRumoqIi\nBQL1n1a1d+9eXXrppd3XWgAA+pE2h6MzMjKUnp6uWbNmybIsZWdnKz8/XwkJCZo+fbrmzZunOXPm\nyOl0atKkSZo8eXJPtBsAgD7PsptO8vaA7h7z7+/zCq2h5ugRjXVTc3To7zV3ek4YAAB0D0IYAABD\nCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDA\nEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEA\nMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEA\nAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIY\nAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAxxtWen3Nxc\n7dmzR5ZlKSsrSxMmTIhsO3LkiO677z7V1dXp8ssv1yOPPNJtjQUAoD9p8054165dKi4u1pYtW5ST\nk6OcnJxm21evXq1bb71VL774opxOpw4fPtxtjQUAoD9pM4QLCgqUmZkpSUpLS1NFRYUqKyslSeFw\nWH/84x913XXXSZKys7M1dOjQbmwuAAD9R5vD0WVlZUpPT48sJyUlqbS0VPHx8Tp+/Lji4uL06KOP\nqrCwUJMnT9b9999/3vMlJvrkcjkvvOXn4fcndOv5eyNqjh7RWDc1R4dorLldc8JN2bbd7PnRo0c1\nZ84cDRs2TPPnz9eOHTs0derUcx5fXl7VqYa2l9+foNLSU916jd6GmqNHNNZNzdGhv9d8rl8w2hyO\nTklJUVlZWWS5pKREfr9fkpSYmKihQ4dq5MiRcjqduuqqq/SnP/2pi5oMAED/1mYIT5kyRdu3b5ck\nFRYWKiUlRfHx8ZIkl8ulESNG6KOPPopsT01N7b7WAgDQj7Q5HJ2RkaH09HTNmjVLlmUpOztb+fn5\nSkhI0PTp05WVlaVly5bJtm1ddtllkTdpAQCA82vXnPDixYubLY8bNy7y/JJLLtGmTZu6tlUAAEQB\nPjELAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEA\nMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEA\nAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIY\nAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAxxmW4AAKBnHTlyWHPmzNLYseMkSXV1dRo1arQW\nL14mp9PZoXNdf/0X9PLLrzZbd9dd8xUIBBQTExNZ9/DDuUpOHnRB7X7vvd265JJLlZiYpGXL7tPq\n1Wsu6Hy9ASEMAFFo5MhLtG7ds5HlnJyV+s1vtukf/uH6Ljl/VtZDGjVqdJecq9HLL7+kr33t60pM\nTOoXASwRwgAASZdfPl4ff3xIkrR16/P67W+3ybIc+vznp+prX/u6SkqO6rvffUiSFAwGtWLFwxo2\nbHiHrjFjxo36j//YIp/Pp3XrfqBRo9IkSe+//56qqk7pwIEi/cu/fEM33HCT/vCHnVq//hk5HA5l\nZv6dUlNH6fXXd+gvf/mzVq16TPPmzdbLL7+qoqIDWrPmX2VZlny+OK1YsVIHDvxJ+fnPy7IcKi7+\ni6ZO/YJuvXV+175gXYQQBgCDVr61Qv9V9Mtm6xwOS+Gw3elz3ph2k1Zevard+weDQb3++v/oppu+\nosOHP9GOHa/qmWc2SJLuuGOepk3LVHn5Mc2de5syMibrV7/6T+Xnv6C77763021sqqjogLZufUHv\nvvuBsrOzdP31X9ITT/yrfvjDH2vAgAFavvx+felL/6zRoy/Tffct0eDBgyPHrl37uO688x6lp4/X\nz3/+U73wwmZNmvQZffBBoX7+860Kh8P66ldvJIQBAL3HwYPFuuuu+mAqKjqg2bPn6JprpurVV1/R\nxx8f0t133y5Jqqo6rU8/PawhQ4bqBz94XBs2rNepUyc1duxfnff8ubmPNJsTXrv2h+fcd/z4CXI6\nnfL7U3T6dKVOnCiXx+NRYmKiJOmxx35wzmM/+ugvSk8fL0nKyJis5557VpMmfUZjx45rdv3eihAG\nAINWXr2qxV2r35+g0tJT3XrdpnPCK1Ys0YgRl0iSXC63rrpqipYsebDZ/rm5D+vKK/9WN900Q6+9\n9lu99dYb5z1/a3PClmVFngeDwcjzpm8Gs21bDoejUyMBwWCdHA5Hi3P2ZvyJEgBEuTvvvEf/9m9P\nKRAIaOzYv9Lu3X9UIBCQbdv6wQ8eV01NQCdOnNCwYcNl27beeON/VFdX1+Hr+HxxOnasTKFQSIWF\n/3vO/QYOvEjhcEilpSWybVtLlizSqVOn5HA4FAqFmu2bmpqmvXvflyS9++7uNu/QexvuhAEgyg0d\nOkxTp35BGzdu0O23L9TNN39NCxfeJofDoWuumSqvN0Zf+tI/6/vf/54GDx6qGTNm6rHHcrRr184O\nXecrX7lZS5feq5EjL1Fq6qjz7nv//cu0YsVSSdJ112UqISFBV1yRoRUrlurRR5+I7Ldo0eLIG7MS\nEhKUlZWtffs+7PiLYIhl23bnZ/87obuHWHpiGKe3oeboEY11U3N06O81+/0Jra5nOBoAAEMIYQAA\nDCGEAQAwhBAGAMAQQhgAAEMIYQAADOHvhAEgypz9VYa1tbWaPfsWXXvttA6fa+vWLTpx4oSuuWaq\nfv/7HZo37/ZW93vjjf/RlVdeLbfb3eY5//znA1qz5rFm3/IkSddee6X++q8nRpaTk5P18MOPdrjN\nZ3vttd9q2rRM/elP+85bQ3cghAEgCjX92MqTJys0d+5s/e3fXiWvt3OftzxmzFiNGTP2nNs3b85T\nRsbftCuEzyU+Pr5FMHeFn/1so6ZNy2yzhu7QrhDOzc3Vnj17ZFmWsrKyNGHChBb7PPHEE3rvvff0\n05/+tMsbCQDoPgMGDFRy8iAdO3ZMzz33I7lcbp08eUKPPLJajz2Wo8OHP1EwGNS3vrVAn/nM3+id\nd3bpySefUFJSspKTB2no0GHavfsd5ec/r1WrHtO2bS/rxRe3yLIszZo1W3V1dfrgg71avPjbWrv2\nh3rppV+0+KrETz/9VHfeeZfcbrdGj76s3W0/cuSwVqxYqg0b6rNn3rxvaNWqf9WPf/ysBg3ya9++\n/9PRo5/qoYdWaezYccrL26gdO16VZTm0YMFd+vDDD3TgwH5lZT2gGTNmRmp49dXfaMuWPDmdTo0d\n+1datGixNmxYr9OnK3XwYLE++eRjffvb9+uqq6Zc0GvfZgjv2rVLxcXF2rJli4qKipSVlaUtW7Y0\n2+fAgQP6wx/+cEG/4QBANIpbuULe/2r+VYZyWEq6gK8yrLnxJp1e2f6vMjxy5LBOnqxQSsrFkqQB\nAwZo6dIHtW3by0pOHqTlyx/SiRMndM89C7Rx42atX79O3/nOdzVmzGVavPjbGjp0WORcVVWn9ZOf\n/Ls2btyk2to65eRka/XqNfr3f/83Pf74kyotLWn1qxL/+79/oS984e90881f089+9hMdOLC/0/U3\nqq2t1Zo16/TLX76obdtels/n044dr2r9+p/o8OFP9LOf/UTLln1HeXkblZv7Pe3e/U5DDVV69tmn\n9dxzP5fP59OSJfdGtpWUHNXjjz+pnTvf0n/+59buD+GCggJlZmZKktLS0lRRUaHKykrFx8dH9lm9\nerXuvfderVu37oIaAwDoGU2/ytDj8WjFioflctVHwuWXp0uS9u59X3v2vKv3339PklRTU6O6ujod\nOXJEY8bU361ecUWGampqIuf96KO/aOTIS+X1xsjrjdHq1WuaXff//q+w1a9KLCoq0uzZcyVJkyZN\n1s6db7Voc2VlZaTNkpSWNlqzZn39nDVOnDhJkuT3X6wPPijU/v37dPnl4+VwODR8+AgtW/adVo87\ndOighg8fKZ/P19Cez2j//vrPo54w4QpJUkpKiiorK8957fZqM4TLysqUnp4eWU5KSlJpaWkkhPPz\n8/XZz35Ww4YNO9cpmklM9Mnl6t6vmDrXZ3T2Z9QcPaKx7n5d89Nr6/+d5UJ+Svoa/p1LTU2cRo1K\n1ZYtm1psi4lxKzl5gPz+BCUk+HTXXQt1ww03NNvH5XJG+sTn88jlki66yCev163k5AS53Y4WfeZ0\nOjRoULySkwfouuum6ZFHHmm2/YUX8pSUFC+/P0EDB8bI43G1OEdCQkKLNn/yySdyuZpeL6ykpDjF\nxLibnC9WXq9LiYlx8npbnteyLPn9CZEakpLimtXg9Trk9XolBTVwYJz8/gSVl8fJ7XZe8P/NDr8x\nq+n3PZw4cUL5+fl67rnndPTo0XYdX15e1dFLdkh//xDw1lBz9IjGuqm56x0/flrBYLjVawQCdaqo\nqFZp6Smlpo7Vr3+9TVdeea3Ky4/r+ec36fbbFyopaZD++Mf/1YgRl+iNN95Sevpf68SJKtXU1GnA\ngBQdOFCk4uKjcjqdWrr0Xn3/+08rHJaOHq3Q4MGX6s03H9OhQ6Xyer1au/YJ3XHHXUpNTVVBwTu6\n+OJL9Lvf/V61tcEW7bNtu8W6QEAqLS1TSclJHT9+TAcPHtTx46eb1VFRUa1AoE5DhlyqXbvW6ciR\ncp08WaHvfe9RPfro4wqF6l+Lxhri4wfpz3/+i4qLP5XPF6c33ijQLbfM0zvvvC23O6DS0lMqLz/d\nahvP5Vxh3WYIp6SkqKysLLJcUlIiv98vSdq5c6eOHz+u2bNnq7a2VgcPHlRubq6ysrLa1SgAQO91\n3XWZ2r37D1qw4FaFQiHdemv9UPD8+XdqxYqlGjx4SGQeuVFsbKzmzVugRYvulCTNnPkvsixLkyZl\n6M475+mpp55t9asS58yZo4UL79bvf/+a0tLGtLuNAwYM0OTJn9W3vjVHo0ePOe+7m4cMGaq///sv\n6q675su2bd1++0JJ0mWXjdVtt83RHXd8O1LDwoX36P7775ZlOTRhwhWaOPEKvfPO2x16/dqjza8y\n3L17t5566ik999xzKiws1KpVq7RpU8shjI8//ljLly9v893RfJVh16Pm6BGNdVNzdOjvNXf6Tjgj\nI0Pp6emaNWuWLMtSdna28vPzlZCQoOnTp3d5QwEAiBbtmhNevHhxs+Vx48a12Gf48OH8jTAAAB3A\nZ0cDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAA\nhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwA\ngCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggD\nAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDC\nAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGE\nMAAAhrjas1Nubq727Nkjy7KUlZWlCRMmRLbt3LlTa9askcPhUGpqqnJycuRwkO0AALSlzbTctWuX\niouLtWXLFuXk5CgnJ6fZ9oceekhPPvmkNm/erNOnT+v111/vtsYCANCftBnCBQUFyszMlCSlpaWp\noqJClZWVke35+fkaPHiwJCkpKUnl5eXd1FQAAPqXNoejy8rKlJ6eHllOSkpSaWmp4uPjJSnyWFJS\nojfffFP33HPPec+XmOiTy+W8kDa3ye9P6Nbz90bUHD2isW5qjg7RWHO75oSbsm27xbpjx45pwYIF\nys7OVmJi4nmPLy+v6uglO8TvT1Bp6aluvUZvQ83RIxrrpubo0N9rPtcvGG0OR6ekpKisrCyyXFJS\nIr/fH1murKzUbbfdpkWLFulzn/tcFzQVAIDo0GYIT5kyRdu3b5ckFRYWKiUlJTIELUmrV6/WLbfc\nomuuuab7WgkAQD/U5nB0RkaG0tPTNWvWLFmWpezsbOXn5yshIUGf+9zn9Mtf/lLFxcV68cUXJUk3\n3HCDZs6c2e0NBwCgr2vXnPDixYubLY8bNy7yfO/evV3bIgAAogSfqgEAgCGEMAAAhhDCAAAYQggD\nAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDC\nAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGE\nMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAI\nIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY\nQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY0q4Qzs3N1cyZMzVr1iy9\n//77zba99dZbmjFjhmbOnKmnn366WxoJAEB/1GYI79q1S8XFxdqyZYtycnKUk5PTbPuqVav01FNP\nadOmTXrzzTd14MCBbmssAAD9iautHQoKCpSZmSlJSktLU0VFhSorKxUfH69Dhw5p4MCBGjJkiCTp\n2muvVUFBgUaPHt29rW5gHT2quNyHZZ0+fWal16WEmmCPXL/XoOZWWbbdQ43pQV6XBkRhX1NzFOhF\nNYcGD9bph3MlV5sRecHavEJZWZnS09Mjy0lJSSotLVV8fLxKS0uVlJTUbNuhQ4fOe77ERJ9cLucF\nNLmJfXuk5zdJoVCz1TFdc/Y+hZqjh9d0Awyg5ujQa2qOj5dvdY6UlNDtl+pwzNsXeHdRXl51Qcc3\nM3airP3FUqAmsmrQoHiVlVV23TX6AGo+D8vq/sb0IPo6OlCzWXZcnBRyS6Wnuuycfn/rgd5mCKek\npKisrCyyXFJSIr/f3+q2o0ePKiUl5ULb2iF2wgCpaW3+BNlWbI+2wThqjh7+BNnRNgZAzdEhGmtW\nO96YNWXKFG3fvl2SVFhYqJSUFMXHx0uShg8frsrKSn388ccKBoN67bXXNGXKlO5tMQAA/USbd8IZ\nGRlKT0/XrFmzZFmWsrOzlZ+fr4SEBE2fPl0rV67U/fffL0n64he/qNTU1G5vNAAA/YFlX+gkbweV\nduEYe2v8/oRuv0ZvQ83RIxrrpubo0N9rPtecMJ+YBQCAIYQwAACGEMIAABhCCAMAYAghDACAIYQw\nAACGEMIAABhCCAMAYEiPf1gHAACox50wAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABjiMt2A\n9sjNzdWePXtkWZaysrI0YcKEyLa8vDy99NJLcjgcGj9+vB588EEFg0E9+OCDOnjwoEKhkJYsWaLJ\nkyfrww8/1MqVKyVJY8eO1cMPP2yoorZ1Vc3f+MY3VFVVJZ/PJ0launSpxo8fb6qs8+pozceOHdPS\npUtVU1Ojuro6LV++XBMnTuzX/XyumvtSP0sdr7tRWVmZ/vEf/1Hr1q3TlVde2a/7utHZNfelvu5o\nzfn5+Vq7dq1GjhwpSbr66qt1xx139Kl+7jC7l3v77bft+fPn27Zt2wcOHLBvvvnmyLZTp07Z06ZN\ns+vq6mzbtu25c+fa7777rv3iiy/a2dnZtm3b9v79++2vfOUrtm3b9te//nV7z549tm3b9n333Wfv\n2LGjBytpv66ued++fT1bQCd0puYf//jH9ksvvRQ5fu7cubZt9+9+Pl/NfaGfbbtzdTd64IEH7C9/\n+cv2zp07bdvu333dqLWa+0Jfd6bmrVu32qtXr25xrr7Sz53R64ejCwoKlJmZKUlKS0tTRUWFKisr\nJUlut1tut1tVVVUKBoOqrq6tWmLVAAAEKklEQVTWwIED9U//9E9avny5JCkpKUknTpxQbW2tPvnk\nk8hvYtOmTVNBQYGZotrQVTX3JZ2pee7cubrxxhslSUeOHNHFF1/c7/u5tZr7ms7U3XhcXFycLrvs\nMknq933deFzTmvuSztZ8tr7Uz53R64ejy8rKlJ6eHllOSkpSaWmp4uPj5fV6tXDhQmVmZsrr9er6\n669Xampqs+M3btyoG264QeXl5RowYEBkfXJyskpLS3usjo7oqpobPfnkkyovL1daWpqysrIUExPT\nY7W0V2drLi0t1YIFC3T69Glt3LgxKvr57Job9YV+ljpXd21trZ5++mk988wzys3NlaR+39et1dyo\nL/R1Z2p+9913tWvXLs2bN0/BYFBLly5VcnJyn+nnzuj1d8Jns5t8ymZlZaXWr1+vbdu26dVXX9We\nPXv04YcfRrbn5eWpsLBQCxcuPO95ersLqXnOnDlasmSJ8vLyZFmW8vLyerz9ndHemv1+v7Zu3arl\ny5dHRgLOdZ7e7kJq7qv9LLWv7meffVZf/epXm/0wPt95ersLqbmv9nV7ap44caLuvvtubdiwQYsW\nLdLSpUvPe57+oNffCaekpKisrCyyXFJSIr/fL0kqKirSiBEjlJSUJEmaPHmy9u7dq3HjxumFF17Q\n7373Oz3zzDNyu90thmiPHj2qlJSUni2mnbqqZkmaPn165DzXXXedfv3rX/dgJe3XmZpPnjypsWPH\nauDAgbr22mu1ZMmSft/PrdUs9Z1+ljpX9xtvvKFwOKy8vDwdPHhQ77//vtasWdOv+7q1mteuXdtn\n+rozNc+YMUNpaWmSpEmTJun48eNKTEzsM/3cGb3+TnjKlCnavn27JKmwsFApKSmKj4+XJA0bNkxF\nRUUKBAKSpL179+rSSy/VoUOHtHnzZq1bt05er1dS/RzEqFGj9M4770iSXnnlFX3+8583UFHbuqpm\n27b1zW9+UydPnpQkvf322xozZoyBitrWmZpfeeUV/eIXv5Ak7du3T0OGDOn3/dxazX2pn6XO1b15\n82Y9//zzev755zV16lRlZ2dr3Lhx/bqvW6t59OjRfaavO1Pzj370I/3qV7+SJO3fv19JSUnyeDx9\npp87o9ffCWdkZCg9PV2zZs2SZVnKzs5Wfn6+EhISNH36dM2bN09z5syR0+nUpEmTNHny5MhvyPPn\nz4+cZ8OGDcrKytJDDz2kcDisiRMn6uqrrzZY2bl1Zc0333yzvvnNbyo2NlYXX3yx7r77boOVnVtn\nah41apSWLVum3/zmN6qtrY38CUN/7ufWarYsq8/0s9S5us+lP/d1a/pSX3em5uHDh+uBBx7Q5s2b\nFQwGlZOTI6nv9HNn8FWGAAAY0uuHowEA6K8IYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAw\nhBAGAMCQ/wf8rdEKyu3xWwAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "KjY_KnlE5ClG",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Drive the loss to a minimum."
+ ]
+ },
+ {
+ "metadata": {
+ "id": "JKiHjGN15HPX",
+ "colab_type": "code",
+ "outputId": "5d36ee4a-7956-435f-a8ad-1f5f4e94ae99",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 555
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.006, n_epochs=100000, interval=10000)"
+ ],
+ "execution_count": 0,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.19373068\n",
+ "Loss after epoch 10000 is 4.036964e-06\n",
+ "Loss after epoch 20000 is 4.017399e-06\n",
+ "Loss after epoch 30000 is 4.017399e-06\n",
+ "Loss after epoch 40000 is 4.017399e-06\n",
+ "Loss after epoch 50000 is 4.017399e-06\n",
+ "Loss after epoch 60000 is 4.017399e-06\n",
+ "Loss after epoch 70000 is 4.017399e-06\n",
+ "Loss after epoch 80000 is 4.017399e-06\n",
+ "Loss after epoch 90000 is 4.017399e-06\n",
+ "Testing the Model\n",
+ "The final loss is: 3.4938046e-06\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAewAAAFKCAYAAADfb2yTAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3XdAVfX/x/HnXcx7QVBw4lZKzBVl\naebCXJlZqVg5KRP3RnGXI82Fe6S5KLW0tFxkqWmhZq5Q0UIFtyAg9zLv+v1BP76ZE2Rc4P34Jy73\n3M/n8+aSL97nnHuOwmq1WhFCCCGETVMW9AKEEEII8XgS2EIIIUQhIIEthBBCFAIS2EIIIUQhIIEt\nhBBCFAIS2EIIIUQhoC7oBTxKbKw+T8d3c3MiISElT+ewNVJz8VEc65aai4+iXLeHh+6B3y/WHbZa\nrSroJeQ7qbn4KI51S83FR3Gsu1gHthBCCFFYSGALIYQQhYAEthBCCFEISGALIYQQhYAEthBCCFEI\nSGALIYQQhYAEthBCCFEI2PSFU2zRjRvX6dHDH2/vZwAwGo1UrVqdkSPHoFJl73OB7du3ZMeOn+75\n3sCBfUlLS8PBwSHre1OmTKdkyVJPte6TJ49TqVJlPDx0jBkznE8/nftU4wkhhMhfEtg5ULFiJRYt\nWpH1eNq0yfz4427atGmfK+MHB0+katXquTLW/9uxYzvdur0PVJKwFkKIQkgCOxfUqlWbq1evALBl\ny2b27t2NQqGkSZNmdOv2Prdv3+KTTyYCYDKZGD9+CuXLV8jWHO+804F16zbh5OTEokXzqVq1GgCn\nT58kMTGBmJho3n23O6+//ia//36Y5cuXoFQq8fN7jSpVqnLw4H4uXbrI0qWLefPNN9mx4yeiov5m\n7tyZKBQKnJycGT9+Mn///Rdbt25GoVASHX2JZs1a0qdP39z9gQkhhMi2Qh3Yk38bz/dR3+X49Uql\nAovFes/3OlR7k8mNpj7xGCaTiYMHD/Dmm29z/fo19u//iSVLVgEQGBhA8+Z+JCTcoXfvD2nQwJcf\nftjG1q1fM2jQsByv+9+iov5m2bLVXL16hUmTgmnfviNz5sxk6dLVuLi4MHbsCDp2fIvq1WsyfPho\nypUrl/XakJDZ9O8/BB+f2nz55Xq+/noj9es/z9mzZ/jyyy1YLBY6d+4ggS2EEA+guHULuwM/k/7m\n22Bnl+fzFerALigxMdEMHJgZYlFRf/Peez149dVm/PRTGFevXmHQoI8ASElJ5ubN65QtW47582ez\natVy9PokvL2ffeT406d/fM8x7JCQpQ/dtnbtOqhUKjw8PElONpCYmICdnR1ubm4AzJo1/6GvvXz5\nEj4+tQFo0MCXL75YQf36z+Pt/cw98wshhPgXqxX7LZvRBo9CmZhIQk1vTPUa5Pm0hTqwJzeamq1u\n+L88PHQ5uiPYv49hjx8/Gi+vSgCo1Rpefrkxo0ePu2f76dOn0LDhS7z55jvs27eX33479MjxH3QM\nW6FQZH1tMpmyvv73iW5WqxWlUnnfXoMnYTIZUSqV940phBDifxS3b6MbNRT7XT9gdXJCP2M2prr1\n82Vu+VjXU+rffwjLli0kLS0Nb+9nOX78D9LS0rBarcyfP5v09DQSExMpX74CVquVQ4cOYDQasz2P\nk5Mzd+7EYTabOXPmz4du5+paAovFTGzsbaxWK6NHD0Wv16NUKjGbzfdsW6VKNSIiTgNw4sTxx3b+\nQghRbFmt2H/7De6vvoj9rh/IeLkx8ft+Iy2gL/yrocpLhbrDtgXlypWnWbOWrF27io8+GkCXLt0Y\nMOBDlEolr77aDHt7Bzp2fIt58z6jTJlyvPNOV2bNmsbRo4ezNc/bb3chKGgYFStWokqVqo/cdsSI\nMYwfHwRAixZ+6HQ66tVrwPjxQSxfvixru6FDR2addKbT6QgOnsT585HZ/yEIIUQRpoiNRRc0HPsf\ntmF1dEQ/fRZpffqCMn97XoXVas3+/tN8kpPd1dmR013ihZnUXHwUx7ql5uIjv+q237YV7ZgRKO/c\nwdjwZZJClmD551M6ecXDQ/fA70uHLYQQQvyHIi4O7ZgROGz/FqujI4ZPZpD6YWC+d9X/JoEthBBC\n/Ivd99vQBQ1DGReH8cWX0C9YgjmXL2aVExLYQgghBKC4cwft2BE4fLcVq4MDhinTSe0bCDbyyRkJ\nbCGEEMWe3Y7v0Y0aijIuFuPzL6BfuAxz9RoFvax7PFFgT58+nVOnTqFQKAgODqZOnTpZz4WGhrJ9\n+3aUSiW1a9dm3LhxbN26lZCQECpWrAhAo0aNCAwMJDIyksmTJwPg7e3NlClTcr8iIYQQ4gkp4u+g\nDR6Nw9avsdrbY5g0ldR+A2ymq/63xwb20aNHiY6OZtOmTURFRREcHMymTZsAMBgMrFq1irCwMNRq\nNX369OHkyZMAtGvXjqCgoHvGmjZtWlbgjxgxggMHDtC0adM8KEsIIYR4NLtdO9CNHIIy9jbG533R\nhyzFXNO7oJf1UI893S08PBw/Pz8AqlWrxt27dzEYDABoNBo0Gg0pKSmYTCZSU1NxdXV94DgZGRlc\nu3Ytqztv3rw54eHhuVVHvrlx4zqtWr3KwIF9GTiwL3379uLAgX05GmvLlk2sWrWcv/46z6pVyx+6\nXXYutnLx4t9Zl039t6ZNGzJwYF+6d+/OwIF9mTRpbI7W/F/79u0FeGwNQghhKxQJ8ej6f4hrz24o\n7iZimPAxid+HZTusjWYjf8adJr8+Hf3YDjsuLg4fH5+sx+7u7sTGxqLVarG3t2fAgAH4+flhb29P\n+/btqVKlCidOnODo0aMEBARgMpkICgqiZMmSuLi4ZI1TsmRJYmNj86aqPPbvS5MmJd2ld+/3eOml\nl7G3z9n1t2vU8KZGjYf/omzcGEqDBi+g0WhyND6AVqtl0aIVuf7ZxQ0b1tK8ud9jaxBCCFtgF7YL\n7YghqG7dxFi/AfoFyzB7P5PtcWJTYumz532O3Ahnz9v7qF/6+TxY7b2yfdLZv/+SMBgMLF++nN27\nd6PVaunZsyeRkZHUrVsXd3d3mjVrxokTJwgKCuLzzz9/6DgP4+bmhFqdt8cRHvYB9YdJT3dGrVZm\nvc7DQ0eZMqWxWtOYM2cOGo2GxMRE5s+fz4QJE7hy5Qomk4nBgwfz8ssvEx4ezvTp0ylVqhQeHh54\neXlx8eJZQkNDWbBgAd999x3r169HqVTSu3dvMjIyOHs2grFjh7FmzRq+/vprvv/++39unelHnz59\nuHnzJkOGDMHOzg5vb2/s7NT31aVQKO5ZM8DVq1cZPHgwW7duBeCtt95iwYIFLFq0CE9PT86cOcP1\n69eZPXs2Pj4+rFy5kj179qBUKhk+fDgRERFERf3FlClj6d69e1YNO3fuZM2aNahUKnx8fBg/fjwL\nFy5Er9dz6dIlYmJiCA4OztfDIdl9n4uK4li31Fx8ZKvuhAQYOhTWrQONBqZPRzNqFO7q7J97ferm\nKd749g1i7sbQxacLLWq9glqZ9+dwP3YGT09P4uLish7fvn0bDw8PAKKiovDy8sLd3R0AX19fIiIi\neOedd6hWLfNKMPXr1yc+Ph43NzcSExOzxrl16xaenp6PnDshIeWRzztPHo/99zm/vaZKqcD8nxtl\npHd4k+TJD7+hSHx8MiaTJatLvXHjOnfuxKNWa0lLM+Lk5MLEiaP58suvcXZ2Ze7csSQmJjJkSD/W\nrt3IzJmzGDt2MjVq1GTkyMG4u3uSmJhCerqR6OibLFy4iLVrvyIjw8i0aZP49NO5uLvPZ8aMeZw7\nd5Hvv9/BggWZ3X1gYAAvvNCErVs38eqrLenSpRsbNqwhI8N0XxdttVqJjdXf02H/txaTyUJ8fDJp\naUYSEw18+ul8vvvuG7766mveegt27NjJ8uVruH79Ghs2rGHMmAmsWLGCSZNmcPz4sX9quMXs2XP4\n4osvcXJyYvToYezZs4/k5HSio68wffpcDh/+jfXrQ6lVK+/vbgNyJajiRGouPrJTt93ePWiHD0Z1\n8wbGuvXRL1iK+dlakJCa7Xl3XPyeAXs/JMWUwpgXxzPs+VEk3Mn+OI+S4yudNW7cmIULF+Lv78+Z\nM2fw9PREq9UCUL58eaKiokhLS8PBwYGIiAiaNm3KypUrKVu2LK+//joXLlzA3d0dOzs7qlatyrFj\nx/D19SUsLIzu3bvnapH55d+317Szs2P8+Cmo//krrVatzMMHERGnOXXqBKdPZ56El56ejtFo5MaN\nG9SoUROAevUakJ6enjXu5cuXqFixMvb2DtjbO/Dpp3PvmffcuTMPvH3n5cuXaN488zyD+vV9OXz4\nt/vWbDAYGDiwL3Z2ajIyTFSrVh1///cfWmPdf+4+4+FRmrNnz3Dhwnlq1aqNUqmkQgUvxoyZ8MDX\nXbkSQ4UKFXFycvpnPc9z4ULm9cnr1KkHZP4R+P/nQQghRF5R3E3EeWIwjl9twKrRkDxmPCmDhmV2\n2NlktVqZ+8csZh6dhpPaidWtN/B6tTfyYNUP99jAbtCgAT4+Pvj7+6NQKJg0aRJbt25Fp9PRqlUr\nAgIC6NGjByqVivr16+Pr60uFChUYNWoUGzduxGQyMW3aNACCg4OZOHEiFouFunXr0qhRo6dafPLk\nqY/shh/Hw0NH/FPeXvO/1GpN1n979OhDq1Zt7nle+a/L2v33sIBSqcJqtTx03ofdvjM0dC0KhfKf\nMR/8+gcdw75588Y92zzqtp0q1ZPdtlOhuLcuk8mIvb39A8cUQoi8ovn5R3TDBqG6cR3jc3Uzu2qf\n2jkaK8WYwpCf+7MtaisVtF6sa7eR2qWey+UVP94T7XQfOXLkPY+feeZ/B+j9/f3x9/e/5/kyZcqw\nfv36+8apXr06X375ZU7WWejUqlWbQ4cO0KpVGxIS4tm8+Ss++mgApUp5EBNzGS+vSpw48Qc+Pv97\n0ytVqkxMTDQpKSmoVCqCgoYxb95iFIrMW2N6ez/L0qWZt/K0t7cnJGQOgYEDqVixEpGRZ3nmmWc5\nfvzYE6/RycmZhIR4rFYr8fF3uH796kO39fZ+ljVrVmEymUhKustnn81gxozZ94W4l1clrl6NISUl\nGScnZ06cOE7PngEcO3Yk+z9EIYTIJkXSXZwnjcMxdB1WtZrk0cGkDBmRo64a4LrhGj12deN07Eka\nln2Z1a034OHkkcurfjJypbM80qKFH8eP/06/fn0wm8306ZO5C71v3/6MHx9EmTJl8fQsfc9rHB0d\nCQjox9Ch/QHo2vVdFAoF9es3oH//ABYuXPHA23d27tyNCRPG8Msv+6hW7cmvzOPi4oKv74t88EEP\nqlev8cizvMuWLUfr1u0YOLAvVquVjz4aAEDNmt58+GEPAgMHZ9UwYMAQRowYhEKhpE6detStW08C\nWwiR5zT7fkI3bCCq69cw+TxH0oKlmJ+r8/gXPsSxm0fpuetdYlNv896zPZj56lzsVHa5uOLskdtr\nFrOTNaTm4qM41i01Fx//rluhT8J58ngc16/BqlaTMnQkKUNHgl3Ow3VT5JeM2D8Yk9XEx42m82Gd\nQBQKRW4t/5Hk9ppCCCGKHM2BfZld9dUrmJ71Qb9oGabn6uZ4PLPFzNTDk1l8MgQXO1dWvraG5hVb\n5uKKc04CWwghROGj16MdNQzHtauwqlQkDx9NyvDRT9VV6zOS+CisD3tjwqhWojob2m2iWgnbuQGI\nBLYQQohCRXPwAIwYhOPly5ieeRb9wmWY/vkoak5dvBtFj53+XEg4T3Ovlqx47Qtc7Uvk0opzx2Ov\nJS6EEELYBIMBbdBwSrzdAWJiSB46koQff3nqsD549QBtvmnOhYTzfFR3AKHtv7a5sAbpsIUQQhQC\nmt8OoRvcH1XMZUzez6Bev46Uytm/Bvi/Wa1WVkesZPyhIJQKJfObL+bdZ233gl4S2EIIIWxXcjLO\n0ybj9PlyrEolKYOHkzxyDB5eHvAUZ8cbzUbGHhzFurOrKeVYitVtQnmp7Mu5uPDcJ4EthBDCJmnC\nf0U3pD+qy5cw1aiJfsFSTM+/8NTj3km9Q8Ce7vx2/RA+JZ9jXbuv8NJVzIUV5y0JbCGEELYlJQXn\n6VNwXLkMFApSBgwhOWgcOOTsFsb/du7OWbrv8icm6TLtq77BwpbL0Gq0ubDovCeBLYQQwmaoD4ej\nGxKI+tJFTNWqZ3bVLzTMlbF3X9pJ4N4PSDYaGOEbxKgXxqJUFJ5zryWwhRBCFLzUVJxnfILj8sUA\npAQOInnMeHB0fOqhrVYrC0/MY9rhKTioHfj8tbW8Ub3TU4+b3ySwhRBCFCj10SOZXXXU35iqVkMf\nshRTw5dyZexUUyrD9g1k619fU865POvafUUdj3q5MnZ+k8AWQghRMFJTcZ45DcelCwFI+ag/yWMn\ngpNTrgx/M/kGPXd148Tt4zxf+gXWtP2S0k6lH/9CGyWBLYQQIt+pjx1FNzgQ9d9/YapSFUPIEowv\nNcq18U/c+oOeu9/lZvINunh3Y3bTEBzUT3/SWkGSwBZCCJF/0tJwnjUdxyULUFgspPQNJDl4Uq51\n1QBbLmxm2L6BpJvTmdxoGoF1B+bbnbbykgS2EEKIfKE+8Qe6Qf1QXziPuVJl9CFLMDZ6JdfGt1gt\nzDjyCSHH56Czc2F1m/X4VWqda+MXNAlsIYQQeSs9HefPZuC4aD4Ki4XUgL4Yxk8BZ+dcm8KQoaf/\n3g/ZfXknlV2qsKHdZmq6e+fa+LZAAlsIIUSeUZ88nnmsOvIc5oqV0M9fjPGVV3N1juiky/TY6c+5\n+LM0qdCMz19bg5uDe67OYQsKzyfGhRBCFB7p6TjN+JgSbVuijjxHau8PiN8fnuth/du1Q7T+phnn\n4s8S8FxfNrbfUiTDGqTDFkIIkcvUp09mHqs+dxazV8XMrrpJ01yfZ92ZLxhzcAQAs5uG0MOnd67P\nYUsksIUQQuSOjAyc5s7CKWQOCrOZ1B59SJ78CVatLlenMVlMDNo5iEW/L8LdwZ3VrTfQqHzunbxm\nqySwhRBCPDXVn6dxGdQP9dkIzOUroJ+3CGOzFrk+T0JaPB+E9eLg1f08616Lde02Usmlcq7PY4sk\nsIUQQuSc0YjT/Nk4zfsMhclEavdeJE+eilXnkutTXYg/T/ddXbl09yJveL/B/CZL0drlbvduyySw\nhRBC5Igq4k90gwPRRJzGXK48+rkLMbbwy5O59kbv4aMfA9BnJDG0wUjmvD6TO3HJeTKXrZLAFkII\nkT1GI04L5uI0dxYKo5HUd7uT/PF0rC6uuT6V1WplycmFfBw+AXuVPUv9Puftml0K1W0xc4sEthBC\niCemOnsms6s+fRJz2XIY5i4go+VreTJXmimNUQeGsun8l5RxLsvaNl9Sv/TzeTJXYSCBLYQQ4vFM\nJpwWzsNp9qcojEbS/N/D8MkMrK4l8mS6Wym36LXrXf649Tv1PRuwtu1XlHEumydzFRYS2EIIIR5J\nFXkO3eB+aE6ewFy6TGZX3apNns13OvYkPXZ243ryNd6q0Zl5zRfhqHbMs/kKi+J3EEAIIcSTMZlw\nXDAXN78maE6eIK1LNxIOHsnTsN7+97d0+LY1N5KvM/6lySz1+1zC+h/SYQshhLiP6nwkuiGBaI7/\ngdmzNIY5C8ho3TbP5rNYLXz2+wzmHJuJs0bLunYbaV057+YrjJ4osKdPn86pU6dQKBQEBwdTp06d\nrOdCQ0PZvn07SqWS2rVrM27cuKzn4uLiaNu2LYsWLaJhw4Z0796dlJQUnP6572lQUBC1a9fO5ZKE\nEELkmNmM45KFOM+ahiI9nbR3umKYNhOrW95dn9tsMTN03wA2nf+Sii6VWd92I8+WrJVn8xVWjw3s\no0ePEh0dzaZNm4iKiiI4OJhNmzYBYDAYWLVqFWFhYajVavr06cPJkyepV68eALNmzcLLy+ue8WbM\nmEHNmjXzoBQhhBBPQ/XXhcwzwP/4HYuHJ0mzQ8ho2z5P5zRbzAz+OZCvL2ykgefzhLb/hpKOJfN0\nzsLqsceww8PD8fPL/CB8tWrVuHv3LgaDAQCNRoNGoyElJQWTyURqaiqurq5Zr3N2dpZwFkIIW/dP\nV+3WojGaP34n7a13iD94JF/CeuBPH/H1hY08X/oFNnf4TsL6ER4b2HFxcbi5uWU9dnd3JzY2FgB7\ne3sGDBiAn58fzZs3p27dulSpUoWMjAwWL17MsGHD7htvwYIFvPfee0ycOJG0tLRcLEUIIUR2qaL+\nosQbbdBOHodV58LdL0LRL1uN1T1vg9NkMTHgpw/Z8tdmfEu/yOYO3+Jin/sXXilKsn3SmdVqzfra\nYDCwfPlydu/ejVarpWfPnkRGRrJ37146d+6Mi8u915Lt0aMH3t7eVKxYkUmTJhEaGkpAQMBD53Jz\nc0KtVmV3idni4VF8rkP7/6Tm4qM41i01PyGzGRYsgOBgSEuDrl1RLlqEa6lSub/A/zBZTLy/9X22\n/vUNjb0as+u9Xejss19DcXuvHxvYnp6exMXFZT2+ffs2Hh4eAERFReHl5YW7e+bJCL6+vkRERHDo\n0CEsFguhoaHExMRw+vRpQkJCaNWqVdY4LVq0YOfOnY+cOyEhJUdFPSkPDx2xsfo8ncPWSM3FR3Gs\nW2p+MqqLf6Mb3B/N0cNYSpZEv3gFGR3eBCuQxz8/o9lI4N4P2B71LQ3Lvsz61ptJS4I0sjdvUX6v\nH/aHyGN3iTdu3Jg9e/YAcObMGTw9PdFqtQCUL1+eqKiorF3bERERVK5cmY0bN7J582Y2b95Ms2bN\nmDRpEtWrV6dXr14kJSUBcOTIEWrUqJErxQkhhHgCFguOK5bg1rwxmqOHSXujE/EHf88M63xgNBvp\ntzeA7VHf8lLZRnz1+pZidbetp/XYDrtBgwb4+Pjg7++PQqFg0qRJbN26FZ1OR6tWrQgICKBHjx6o\nVCrq16+Pr6/vA8dRKBR06dKFXr164ejoSOnSpRk0aFCuFySEEOJ+yksX0Q0dgF34r1jc3dEvWEp6\nx7fybX6j2UjfH3uz4+J2GpV7hQ3tN6PVaPNt/qJAYf33QWkbk9e7O4ryLpWHkZqLj+JYt9T8ABYL\nDqtXoJ06GUVKCunt30A/cy5WT898W2OGOYO+Yb3Zeel7Gpdrwob2m3HWOD/VmEX5vX7YLnG50pkQ\nQhRRysuXMrvq3w5hcXNDP28R6W++DQpFvq0hw5zBB2E92X1pB03KN2V9u004aZzybf6iRK4lLoQQ\nRY3FgsPqlbg3a4Tdb4dIb/s68b8cJb3TO/ka1unmdAL2dGf3pR28WqG5hPVTkg5bCCGKEGVMNLph\nA7E7eABLiRLo53xO+lud8zWo4Z+w3t2dsOjdNK3QnHXtNspNPJ6SBLYQQhQFVisOa1fjPGUCymQD\n6a3bYpgdgqV0mXxfSpopjT6732dvTBjNvVqypu2XEta5QAJbCCEKOeWVGHTDBmH3yz4sriVIWrSc\n9M7++d5VQ2ZY99r9Lj/H7KVFRT/WtPkSB7VDvq+jKJLAFkKIwspqhZUrcRs+AqVBT3qr1hjmLMBS\npmyBLCfVlErPXd3Yf+Vn/Cq+xuo2GySsc5EEthBCFELKa1fRDRsI+38GF1eSFiwlveu7BdJVQ2ZY\n99jpz4Gr+2hVqTWr22zAXmVfIGspquQscSGEKEysVhxC1+H26kvY7f8Z2rYl4eAR0v3fK7CwTjGm\n0P2fsG5dua2EdR6RwBZCiEJCef0art3ezuysAf38xbBjB5ay5QpsTZlh3ZVfru6jTZX2rGq9XsI6\nj8gucSGEsHVWK/YbQ9FOGIsy6S4ZzVqgn7cIS/kK6AqoqwZINibTfWdXDl37hbZVXmfla2uwU9kV\n2HqKOglsIYSwYcob19GOGIz93jAsWh36uQtJe69Hge3+/n/JxmTe29GZ364fon3VN1jR6gs0Kk2B\nrqmok8AWQghbZLViv/krtOPHoLybSMarzdHPX4SlgldBrwyD0cB7OzoTfv1XOlR7k2V+qySs84EE\nthBC2BjlrZtoRw7Bfs8uLM5a9LNDSOveq8C7agBDhp5uO97hyI1wOlZ7iyV+KyWs84kEthBC2Aqr\nFfstm9EGj0KZmEhGk6aZx6orVirolQGZYe3/w9scvXmYTtXfZrHfStRKiZH8Ij9pIYSwAYpbt9CN\nGor97h1YnZzRz5xLWs8+oLSND/PoM5Lw/+Ftfr95hLdqvMOiliskrPOZ/LSFEKIgWa3Yf/sN2rEj\nUSYkkNG4Cfr5i7FUqlzQK8uSlH6Xrj+8xR+3fuftGl1Y2HKZhHUBkJ+4EEIUEMXt2+hGD8N+5/dY\nnZzQz/iMtN4f2kxXDXA3PZGu33fi+O0/6FzTnwUtlqJSqgp6WcWSBLYQQhQA+21b0QYNRxkfT8bL\njTO76ipVC3pZ97ibnkiX79/kxO3jdPHuRkjzJRLWBUgCWwgh8pEiLg5d0HDsv/8Oq6MjhmkzSQ34\nyKa6aoDEtAS6fP8mJ2NP4P/Me8xrtkjCuoBJYAshRD6x+/47dEHDUcbFYWz4MkkhS7BUrVbQy7pP\nQlo8nb9/k9OxJ3n3me7Mbb4QpcK2/qAojiSwhRAijynu3EE7ZgQO27ZidXDA8MkMUj/oByrb61gT\n0uJ5Z3tH/ow7xfvP9mR2sxAJaxshgS2EEHnI7oft6EYPQxkXi/GFhugXLMFcrUZBL+uB4tPu8M72\njkTEnaZ7rd581nSehLUNkcAWQog8oIi/gzZ4FA5bv8nsqidPI/Wj/jbZVQPcSb3DO9vf4MydP+np\nE8DMV+dIWNsYCWwhhMhldrt2oBs5BGXsbYzPv4B+4TLM1W2zqwaIS43j7W0dOBd/ht61P+DTJnNQ\n2MBlUMW9JLCFECKXKBLi0QaPxmHLZqz29hgmfkJq4ECb7aoBYlNieWd7B87FnyXgub5Mf+UzCWsb\nJYEthBC5wG7PLrQjBqO6fQtjg+fRL1iGuaZ3QS/rkWJTYnl7++tExp/jw+f6MfWVmRLWNkwCWwgh\nnoIiMQHt+DE4bP4Kq50dhvGTSe0/GNS2/c/r7ZTbvL3tdc4nRNK3TiCfNP5UwtrG2fZvlBBC2DC7\nH3ejHTEE1c0bGOvWzzxW/cyzBb2sx7qVfJO3tr3OX4kX+KjuAD5uNF3CuhCQwBZCiGxS3E1EO2Es\nDhtDsWo0JAdPJGXgUJvvqiH1ys3/AAAgAElEQVQzrDtta8/fiX8RWHcQkxtNlbAuJGz/t0sIIWyI\n5ucf0Q0bhOrGdYx16qFfsBRzLZ+CXtYTuZl8g07b2hOV+DcD6w9lwktTJKwLEQlsIYR4iIuJfzPj\nyFROxB6nprI0Y76LpeX+i5jVKiIC3yNl0BDKuVXBvqAX+gRuGK7TaVt7Lt6NYnD94Yx7aZKEdSEj\ngS2EEP8RmxLLnGOfsu7sF5gsJt6K1jJ/y2W8kuBEGej5ppk/S4fC5lAUKPB0Ko2XriJeOi+8dJWo\noPO652snjVOB1nPdcI1O29pz6e5FhjYYydiGEySsC6EnCuzp06dz6tQpFAoFwcHB1KlTJ+u50NBQ\ntm/fjlKppHbt2owbNy7rubi4ONq2bcuiRYto2LAhkZGRTJ48GQBvb2+mTJmSu9UIIcRTSDYms/zU\nYhaemE+y0cBz9pX5+nBlvLftx6pWc3XwB1x+rzUfpN0gRh/NVf0VruqvcEUfw8nY4xy7dfSB45Z0\nKImXriIVdBWpoPOi4n++drF3zbOarumv0mlbey4nXWL486MIenG8hHUh9djAPnr0KNHR0WzatImo\nqCiCg4PZtGkTAAaDgVWrVhEWFoZaraZPnz6cPHmSevXqATBr1iy8vLyyxpo2bVpW4I8YMYIDBw7Q\ntGnTPCpNCCGejMliYmNkKDOPTuNWyk1KOZZipeZdOofsRH1tP6ZatUlauAz75+rwykPGMFvM3Ey+\nwRV9DFf0MVlBfkUfw1XDFc7Fn+Vk7IkHvtbFzjWrQ6/wgC7d3cE9RyF7VX+FTtvaE510mRG+QYx+\nIVjCuhB7bGCHh4fj5+cHQLVq1bh79y4GgwGtVotGo0Gj0ZCSkoKTkxOpqam4urpmvc7Z2ZmaNWsC\nkJGRwbVr17K68+bNmxMeHi6BLYQoMFarlb3Re/jk8CQi48/hqHZk7LNDGPP9HVw2rMCqUpE8IoiU\nYaPAzu6RY6mUKsrrKlBeV4GXaHTf8xarhdjUWK7qY7iSFMMVw5Wsr68arnA56RJn7vz5wLGd1E7/\ndOheVNBVvCfc6zv4oLQ63Xfd7yv6GDpte52YpMuMemEso14Ym/MflLAJjw3suLg4fHz+dwaku7s7\nsbGxaLVa7O3tGTBgAH5+ftjb29O+fXuqVKlCRkYGixcvZsmSJUyfPh2AhIQEXFxcssYpWbIksbGx\nj5zbzc0JtTpvL+nn4aHL0/FtkdRcfBTHup+05t+v/c7ovaPZf3k/SoWSD+p/wHRFKzwGjYboaHju\nORRr1uDcoAHOubS20rhSm+oPfM5qtRKfGk/03WiiE6O5nHg58+u7/3ydGM35hMgHvtZOZUdF14pU\nLlGZSq6VqORaidUnVxOTdJkpzaYwsenEXKrAthS33+9sn3RmtVqzvjYYDCxfvpzdu3ej1Wrp2bMn\nkZGR7N27l86dO98T0I8a52ESElKyu7xs8fDQERurz9M5bI3UXHwUx7qfpObLdy8x48jHfPv3FgBe\nq9SGiXWCaLAoFMcvumJVqUgZNpKU4UFgbw/5+jO0w0tdA69SNXil1P3P6jOSuKL/pzP/Z5d7bMYN\nouIuEqOPYW/83nu2H/PieAJrDSuSvwdF+ff7YX+IPDawPT09iYuLy3p8+/ZtPDw8AIiKisLLywt3\nd3cAfH19iYiI4NChQ1gsFkJDQ4mJieH06dPMnTuXxMTErHFu3bqFp6fnUxUlhBBPKj7tDvOOfcbq\niJUYLUbqedRnYqNPaH5Zga5Tb1QxlzF5P4N+4TJM9RoU9HIfSGfnQq2SPtQq+b+9nv8OrlRTKtf0\nV4nRR6PV6HixbMOCWqrIA48N7MaNG7Nw4UL8/f05c+YMnp6eaLVaAMqXL09UVBRpaWk4ODgQERFB\n06ZN2bhxY9brx4wZQ6dOnXjmmWeoWrUqx44dw9fXl7CwMLp37553lQkhBJkhtvL0MhYcn0tSxl0q\nulRmXMOJdCzbGpdpU3BctQKrUknKkBEkjxyT2VUXUo5qR6q71aC6m+3eylPk3GMDu0GDBvj4+ODv\n749CoWDSpEls3boVnU5Hq1atCAgIoEePHqhUKurXr4+vr+9DxwoODmbixIlYLBbq1q1Lo0b3n5gh\nhBC5wWwx8/WFjXx6ZCrXk6/hZu/GJ41n0Kv2B2iPHkP3bmNU0Zcx1fRGv2AppgYP/7dLCFugsD7J\nweQCktfHJ4ryMZCHkZqLj+JYt4eHjtu3k9h35Sc+Dp/I2TsR2Kvs6VunP4MbDMPVpMF5+hScVi7D\nqlSSOmAIyaPGgoNDQS89x4rj+wxFu+4cH8MWQojC4sSNEwzdOYJfru5DgYKu3u8S9OI4Kui8UB8O\nRzckEPWli5iq18jsqn1fLOglC/HEJLCFEIXeFX0Mnx6ZyjcXNmHFSnOvlkx4+WNql3oOUlJwnjAW\nxxVLAEjpP5jkoHHg6FjAqxYieySwhRCFVmJaAiHH5/L5n8tIN6dTr0w9gl+YTDOvFgCojx5BN7gf\n6otRmKpVRx+yFNOLcua0KJwksIUQhU66OZ3Vf65k3h+zSExPpILWi7ENJ9CvcQB34pIhNRXnT6fi\nuGwRACn9BpI8doJ01aJQk8AWQhQaFquFb//6hhlHPiFGH42rfQkmvTyVgOf64qB2QKlQoj52FN3g\nQNR//4WpStXMrvqllwt66UI8NQlsIUShcPDqAaaET+B07EnslHYE1h3E0OdH4OaQeeEm0tIgaCol\nZs8Gq5WUvoEkB08Cp4K9taUQuUUCWwhh087eOcMn4RP5KeZHAN6u0YWxDSdQ0aVS1jbq48fQDQ6E\nC+exVK6CfsFSjC/JdR5E0SKBLYSwSdcN15h5dBobI0OxYqVJ+aZMfPlj6nrW/99G6ek4fzYDx0Xz\nUVgsMGgQ8cODwTm3btchhO2QwBZC2JSk9LssPDGf5acWk2ZO41l3HyY1+pjmXn733MtZfeKPzGPV\n5yMxV6yMPmQxJd5sl8836xAi/0hgCyFsQoY5g7VnVjHn2Ezi0+Ip61yOsQ0n0LmmPyrlv26zm56O\n05yZOC2ch8JsJrXPhxjGT4F/7nEgRFElgS2EKFBWq5XtUd8y9fBkopMuo7NzYfxLk/nguX44ae49\nYUx96kRmV33uLOaKldDPW4SxSdMCWrkQ+UsCWwhRYMKv/8qU38Zz/PYfaJQa+tYJZNjzoynpWPLe\nDTMycJo7E6eQuZlddc8Akid9jFX74GsuC1EUSWALIfLd+fhIph6exJ7LuwDoWO0tgl+aSBXXqvdt\nq/7zFLpBgajPRmCu4JXZVTdtnt9LFqLASWALIfLNrZRbzDo6jdBz67BYLbxcrjETX/6Y50u/cP/G\nGRk4zfsMp5A5KEwmUrv3JnnyJ1h1Lvm/cCFsgAS2ECJfHL4RTp/d7xGXGkdNN28mvPwxr1Vqc8+Z\n3/9PFfEnLoP6oT7zJ+byFdDPXYixecsCWLUQtkMCWwiR5748t55RB4ZisVr4uPF0PniuH2rlA/75\nMRpxCpmD09xZmV31+z1JnjwVq4tr/i9aCBsjgS2EyDMmi4kp4RNYfmoxJexLsKr1eppUePBZ3aqz\nZ9AN6ofmz1OYy5ZDP28hxhat8nnFQtguCWwhRJ5ISr9L3x9783PMXmqUqMn69puo6lrt/g2NRpwW\nzsNpzkwURiOp3d4n+ePpWF1L5P+ihbBhEthCiFx3MfFvuu/056/EC7Ss2IrlrVbjYn//bm3VubPo\nBgeiOXUCc5myGOYuIMOvdQGsWAjbpyzoBQghipYDV/bRZksL/kq8QGDdQWxot/n+sDaZcAyZg1ur\nV9GcOkFa13dJ+OWwhLUQjyAdthAiV1itVlZHrGT8oSBUChULWizF/5n37ttOdT4S3eB+aE4cx1y6\nDIY5IWS81rYAVixE4SKBLYR4akazkbEHR7Hu7GpKOXqwps2XvFi24b0bmUw4LlmI86xpKDIySHun\nK4ZpM7G6uRfMooUoZCSwhRBP5U7qHQL2dOe364fwKfkc69ttpILO655tVBfOZ3bVx//A4uFJ0uwQ\nMtq2L6AVC1E4SWALIXIsMv4c7+/sSkzSZdpXfYNFLZfjrPnXvajNZhyXLsJ55lQU6emkvdUZw/RZ\nWN1LPnxQIcQDSWALIXIk7PIu+v34AQajnhG+QYx6YSxKxf/OY1X9/VfmGeDHjmIp5UHSsvlktO9Q\ngCsWonCTwBZCZIvVamXRyRCmhk/CQe3AytfW0LH6W//bwGzGcfkSnD/9BEVaGmmd3sYwfTbWktJV\nC/E0JLCFEE8szZTGiP2D+frCRso6l2Nd26+o61k/63lV1F/oBvdH8/sRLKVKkbR4JRkdOhbgioUo\nOiSwhRBP5FbKLXrtepc/bv1OA8/nWdv2K0o7l8l80mLBceVSnKdNyeyq3+iE4dM5WEuVKthFC1GE\nSGALIR7rdOxJeuzsxvXka7xTsytzmy3EQe0AgPJiFLqhA7A7/BuWkiVJWrScjDc6FfCKhSh6JLCF\nEI+0/e9vGfRzP9JMaYx/aQqD6g/NvCWmxYLD6hVoP5mEIjWV9Nc7op85F6uHR0EvWYgiSQJbCPFA\nFquF2b9/yuxjn+Ks0bKu3UZaV868Ipny8qXMrvq3Q1jc3NDPX0z6m2/DA+5tLYTIHU8U2NOnT+fU\nqVMoFAqCg4OpU6dO1nOhoaFs374dpVJJ7dq1GTduHHfu3CEoKIj09HSMRiNjx46lbt26dO/enZSU\nFJycnAAICgqidu3aeVOZECLHko3JDPqpHz9c3EZFXSXWt9vEsyVrZXbVX3yO9pOJKFJSSG/XAf2s\neVg9PQt6yUIUeY8N7KNHjxIdHc2mTZuIiooiODiYTZs2AWAwGFi1ahVhYWGo1Wr69OnDyZMnOXHi\nBB07dqRDhw4cPXqUkJAQVq9eDcCMGTOoWbNm3lYlhMixq/or9NjVjYi40zQq9wqrWq+npGNJlNGX\nM7vqXw9iKVEC/ZwFpL/VWbpqIfLJYwM7PDwcPz8/AKpVq8bdu3cxGAxotVo0Gg0ajSara05NTcXV\n1ZXevXtnvf7GjRuULl067yoQQuSa328eodeu94hNvU33Wr2Y0WQ2dgp1Zlc9ZQKKlGTS27TD8Nl8\nLKXLFPRyhShWHhvYcXFx+Pj4ZD12d3cnNjYWrVaLvb09AwYMwM/PD3t7e9q3b0+VKlUAiI2NpV+/\nfiQnJ7N27dqs1y9YsICEhASqVatGcHAwDg4OeVCWECK7NkaGMnL/EMxWM9NfmUXAcx+hunoF3dCB\n2B3cn9lVf7aC9He6SlctRAHI9klnVqs162uDwcDy5cvZvXs3Wq2Wnj17EhkZyTPPPIOHhwdbtmzh\nwIEDjB07ltWrV9OjRw+8vb2pWLEikyZNIjQ0lICAgIfO5ebmhFqtylllT8jDQ5en49siqbn4eJK6\nzRYzY/aOYXb4bEo4lGDzO5tpVdUPVqyAkSPBYIDXX0e5fDku5crlw6qfTnF8r4tjzVD86n5sYHt6\nehIXF5f1+Pbt23j887GNqKgovLy8cHfPvD2er68vERERJCUl4e3tjaurK02bNmX06NEAtGrVKmuc\nFi1asHPnzkfOnZCQkv2KssHDQ0dsrD5P57A1UnPx8SR16zOS+CisD3tjwqheogbr222kRpIDGc1b\nYndgHxYXVwwLl5HepVtmV23jP8fi+F4Xx5qhaNf9sD9ElA/87r80btyYPXv2AHDmzBk8PT3RarUA\nlC9fnqioKNLS0gCIiIigcuXKhIWF8e233wJw/vx5ypYti9VqpVevXiQlJQFw5MgRatSo8fSVCSFy\n5NLdi7Tb4sfemDCae7Vk11t78fnhN9xefQm7A/tI93uNhINHSO/6ruwCF8IGPLbDbtCgAT4+Pvj7\n+6NQKJg0aRJbt25Fp9PRqlUrAgIC6NGjByqVivr16+Pr60vVqlUZM2YMP/74IxkZGUyePBmFQkGX\nLl3o1asXjo6OlC5dmkGDBuVHjUKI/zh07RcCdncnIT2Bj+r0Z0rlQNx69sFu309YdC4khSwh3f89\nCWohbIjC+u+D0jYmr3d3FOVdKg8jNRcfD6t7TcQqgg+NQoGCWU3mEnBKifOEsSj1SWS08EM/dyGW\ncuULYMVPrzi+18WxZijadT9sl7hc6UyIYsJoNjL+1yC+iPickg4l+ap+CK9OXYv9Tz9i0erQz1tE\n2rvdpasWwkZJYAtRDCSkxfPBnp4cvHaAZ91qsSP9XSp1HoAy6S4ZTZujn7cISwWvgl6mEOIRJLCF\nKOIuxJ/n/Z1duJx0iXdLtGTldgVOP43H4qxFPzuEtO69pKsWohCQwBaiCPspOoy+P/ZBn57EhqS2\ndJv3G8q7d8lo0gz9/EVYvCoW9BKFEE9IAluIIshqtTLntzmM3juaiskaTv9al8q/7sLq5Ix+1jzS\nevaRrlqIQkYCW4giJt2czqgDQ9l4LpTA866E7LSgSTpFxiuvZh6rrlS5oJcohMgBCWwhipDbKbfp\nvfs9ov8+ws97S9D8ZGJmV/3pHNJ6BYDysddKEkLYKAlsIYqIP+NO02NHV5ocvsZPe+zQGRLJaPQK\n+vmLsVSuUtDLE0I8JQlsIYqAH6K2M2Xbh4RsS+Xtc2B1VMPCOdzt3F26aiGKCAlsIQoxq9XK3D9m\ncXH1NH7fCR4pkPFSI/QhSyj5Yl2bv1mHEOLJSWALUUilGFOYuC2A9ot28OlZMDvYY5g6hdQP+klX\nLUQRJIEtRCF0Nz2R5R8347PQi3imQIrv86QtWom5avWCXpoQIo9IYAtRyOhvXCSqT3M++yOBDI2K\nxMmTMX40EFSqgl6aECIPSWALUYiYv9uI64j+tNabuFCjFO5rdmGt4V3QyxJC5AM50CVEIaCIv4PD\nh90p07cvzikm1r9XD5f9kRLWQhQj0mELYePsdu3AeeRg1LGxHC4PG4e2Y0z3UFRK2QUuRHEigS2E\njVIkxKMdF4TDN5tIVysI9oPoXp0J8VshYS1EMSSBLYQNstuzC+2Iwahu3+JMJWc6t0/m2cadWdxS\nwlqI4kqOYQthQxSJCegGfoRr964oExNY/KYXdXsk82zjd1jUcrmEtRDFmHTYQtgIu7170A4fjOrm\nDdLr1KFXJwUbFafoVP1tFrVcgVop/7sKUZzJvwBCFDDF3UScJwbj+NUGrBoN8UFjeKPSAX69Hc6b\n1d9isd9KCWshhOwSF6IgaX7+EbdXX8Lxqw0Y69Tj+q49vF7tIL/eDueNap1Y4ve5hLUQApDAFqJA\nKJLuoh02kBL+b6OMiyU5aBzXtm+n68VJhF//lQ7V3mSphLUQ4l/kXwMh8plm30/ohg1Edf0axtp1\n0C9chr5mVbrv7MKv1w/yetWOLPNbhUalKeilCiFsiHTYQuQThT4J7YjBlOjaCeXtWySPGkvinn3/\nhHVXDl37hfZV32B5q9US1kKI+0iHLUQ+0BzYl9lVX72CqVZtkhYuw/xcHVKMKXTf5c/BawdoV6UD\nK1p9IWEthHgg6bCFyEMKgx7tyKGU6NwR5Y3rJA8fTULYfszP1SHVlEqPXd04eHU/baq0Z8VrEtZC\niIeTDluIPKI5eADd0AGorsRgerYW+gVLMdWtD5AZ1jv9+eXqPtpUbsfnr63FTmVXwCsWQtgy6bCF\nyG0GA9qg4ZR4uwPK69dIHjaShLADWWGdZkqj565uHLi6j9aV2/J563US1kKIx5IOW4hcpPn1ILoh\nA1DFXMbk/Qz6hcsw1WuQ9fz/h/X+Kz/TqlJrCWshxBOTDluI3JCcjHbsSEp0ao/yagwpQ0aQsPfg\nfWHda/e77LvyE34VX2N1mw3Yq+wLcNFCiMLkiTrs6dOnc+rUKRQKBcHBwdSpUyfrudDQULZv345S\nqaR27dqMGzeOO3fuEBQURHp6OkajkbFjx1K3bl0iIyOZPHkyAN7e3kyZMiVPihIiP2nCf0U3OBBV\n9GVMNb0zj1U38L1nm3RzOn12v8/PMXtpWbGVhLUQItse22EfPXqU6OhoNm3axLRp05g2bVrWcwaD\ngVWrVhEaGspXX31FVFQUJ0+eZPv27XTs2JH169czfPhwQkJCAJg2bRrBwcFs3LgRg8HAgQMH8q4y\nIfJaSgrO44NwfbMdyisxpAwaltlVPySs98aE0aKiH1+0CcVB7VBAixZCFFaP7bDDw8Px8/MDoFq1\naty9exeDwYBWq0Wj0aDRaEhJScHJyYnU1FRcXV3p3bt31utv3LhB6dKlycjI4Nq1a1ndefPmzQkP\nD6dp06Z5VJoQeUd9OBzdkEDUly5iql4js6v2ffG+7dLN6QTs7s6P0Xto7tWSNW2+lLAWQuTIYwM7\nLi4OHx+frMfu7u7Exsai1Wqxt7dnwIAB+Pn5YW9vT/v27alSpQoAsbGx9OvXj+TkZNauXUtCQgIu\nLi5Z45QsWZLY2Ng8KEmIPJSSgvOMT3BcsSTzYf/BJAeNA0fH+zbNMGfwwZ4ehEXvpplXC9a2/UrC\nWgiRY9k+S9xqtWZ9bTAYWL58Obt370ar1dKzZ08iIyN55pln8PDwYMuWLRw4cICxY8cyY8aMh47z\nMG5uTqjVquwuMVs8PHR5Or4tkppz6LffoFcv+OsvqFED1qzBqVEjnB6waYY5gy5fd2fP5V20qtqK\nbf7bcNTcH+p5Td7r4qE41gzFr+7HBranpydxcXFZj2/fvo2HhwcAUVFReHl54e7uDoCvry8REREk\nJSXh7e2Nq6srTZs2ZfTo0bi7u5OYmJg1zq1bt/D09Hzk3AkJKTkq6kl5eOiIjdXn6Ry2RmrOgdRU\nnGdOw3HpwsyHHw0geewEcHKCB4ybYc7gw7Be7Lr0A69WaM7nfhswJJowkL8/d3mvi4fiWDMU7bof\n9ofIY086a9y4MXv27AHgzJkzeHp6otVqAShfvjxRUVGkpaUBEBERQeXKlQkLC+Pbb78F4Pz585Qt\nWxaNRkPVqlU5duwYAGFhYTRp0uTpKxMiD6mPHcWt5Ss4LVmAuXIVErftJvmTGZlh/QBGs5G+Yb3Z\ndekHmpRvyrq2X+Gozv/OWghR9Dy2w27QoAE+Pj74+/ujUCiYNGkSW7duRafT0apVKwICAujRowcq\nlYr69evj6+tL1apVGTNmDD/++CMZGRlZH+UKDg5m4sSJWCwW6tatS6NGjfK6PiFyJi0N51nTcVyy\nAKxWUvoGkhw86aFBDf+E9Y+92Xnpe14p/yrr223CSfPw7YUQIjsU1ic5mFxA8np3R1HepfIwUvPj\nqY8fQzc4EPWF85grVUa/YCnGlxs/8jVGs5GPfuzDDxe30bhcEza034yzxvlpl/5U5L0uHopjzVC0\n687xLnEhio30dJynTqZEOz/UF86T8sFHxO8Pf6KwDtz7AT9c3Eajcq/YRFgLIYoeuZa4EID65PHM\nrjryHOaKldGHLMbY+PHnWJgsJvrv/ZDtUd/ycrnGhLb/WsJaCJEnpMMWxVt6Ok7TP6ZE25aoI8+R\n2udD4vf/lo2w/oBtUVt5qWwjCWshRJ6SDlsUW+rTJ9EN6of63FnMXhXRz1+MscmTXXnPZDExYO+H\nfPf3VhqWfZkvX/8GrUabxysWQhRn0mGL4icjA6dPp1KidXPU586S2jOAhAPhTxzWZouZgT99xLd/\nb+HFMi/xVXsJayFE3pMOWxQrqj9P4zKoH+qzEZgreKGftwhj0+ZP/Pr/D+utf33NC2UasvH1LWjt\nitfVloQQBUM6bFE8GI04fTYDt9bNUJ+NILV778yuOpthPfjnQLb8tRnf0i9KWAsh8pV02KLoO3WK\nEu/3QBNxGnP5CujnLsTYvGW2hjBbzAzZ15+vL2zk+dIvsKnDVnR2Lo9/oRBC5BLpsEXRZTTiNGcm\n+PqiiThN6ns9MrvqHIT10H0D2Hz+K54v7cum1yWshRD5TzpsUSSpzp5BNzgQzemTUL48d2eHkNHy\ntWyPY7FaGL5/EJvOf0kDz+fZ9Pq3uNi75sGKhRDi0aTDFkWLyYTTvM9wa/UqmtMnSe32PkRE5Dys\n9w3iq8gN1PdswKYOEtZCiIIjHbYoMlSR59AN7ofm5AnMZcpimLuADL/WOJbQPfA2mI9isVoYsX8w\nX0aup55HfTZ3+A5X+xJ5tHIhhHg86bBF4Wcy4RgyBze/JmhOniCtSzcSfjlMhl/rHA1nsVoYuX8I\noefWUVfCWghhI6TDFoWa6nxkZld94jjm0mUwzA4ho3XbHI9nsVoYdWAYG86tpY5HPb7u8B0lHNxy\nccVCCJEz0mGLwslsxnHh/Myu+sRx0t7pmtlVP2VYjz4wnPVnv+C5UnUlrIUQNkU6bFHoqP66kHkG\n+B+/Y/HwJGl2CBlt2z/VmFarlTG/jGDd2dXULlWHb97YhpuDey6tWAghnp502KLwMJtxXLwAtxaN\n0fzxO2lvdSb+4JGnDmuj2cjoX4az5swqfEo+J2EthLBJ0mGLQkEV9Re6QYFojh3FUsqDpGXzyWjf\n4anHvW64Rt+w3hy9eZhaJWvzzRvbcXcomQsrFkKI3CUdtrBtZjOOyxbh1rwxmmNHSev0NvEHj+ZK\nWO+L+YmWm1/h6M3DvFGtE9932k1JRwlrIYRtkg5b2CzVxb/RDe6P5uhhLKVKkbR4JRkdOj71uGaL\nmc+OzWDesc9QK9XMaDKbPrU/RKFQ5MKqhRAib0hgC9tjseD4+TKcp01BkZpK2hudMHw6B2upUk89\n9K2UWwT+GMCha79QUVeJla+toX7p53Nh0UIIkbcksIVNUV6MQjd0AHaHf8Pi7o5+wVLSO76VK2P/\neu3/2rv3uCjLvI/jnwGG4TAjAgKyiql4xkMYiYfKMFBL89nWct22UMM8RFTaBgoZWovaVh4IUUrc\ndXdJTLPNpy1PYVpPCNkCBRse2BLzCAnCcB7mfv6YYrdaRWgGmJnf+y+Hec113V8vX/74Xfc99/0R\nCw8+wuXaS0ztN43ksFT52pYQwmpIwRZdg9GIy7bX0P5+JaraWhqm/w/VL65D8fH5+UMrRjZ89jJr\nc3+Pg8qBVeNXs2hUtKJdfhgAABt+SURBVGyBCyGsihRs0ekcvv7K1FV/8jFGT0+q16fQ8MuZYIaC\n+m3dt0S+MYt9p/fxC/devDb5T4zxDzXDUQshRMeSgi06j9GIyx+3on0hEVVtDQ13T6f6D+tR/PzM\nMnzuhRwWHJjL+ZpzTOoTzqa7XperwIUQVksKtugUDqVnTF31x0cxdu9O9StbafjVA2bpqhVFITX/\nVZJyVmJUjKyetJpHBj+Gg0q+xSiEsF5SsEXHUhRctm/DfdUKHGr0NEy9B/1LGzD69TTL8JX1FTyR\ntZh9X7+Hr5sfaRHb+OXN91DWxsdrCiFEVyMFW3QYh7Ol6JbE4Hz0MEaP7lRteo2G+39tlq4aIO/S\nZzx6YC6l1We4vddENkek4+vma5axhRCis8keobA8RcHlL3/Cc+I4nI8epmHyVCo+yqHhgdlm2wJP\n/yKN6W9P5mx1KU+HxPHmvX+TYi2EsCnSYQuLcvjmLLqlMTh/mIWxmwdVyZtp+PWDZuuqqxurWHI4\nhr0lb9PDtQep4Vu5M2CSWcYWQoiuRAq2sAxFweWNv+C+YjkO+moa7opAv+5VjP6/MNsUheVfELX/\nYb66+i9C/cfxWsQf8deab3whhOhKpGALs3M4f87UVWcdwqjrRvWGTdT/5iGzddWKovDXL7cT/9Ez\nNDQ3EBO8hOWhK3BykH/OQgjbdUP/w61evZqCggJUKhXx8fGMHDmy5b2MjAz27t2Lg4MDw4cPJyEh\nAYPBQEJCAqWlpTQ3NxMbG0tISAgPP/wwtbW1uLm5ARAXF8fw4cMtk0x0PEVBk5mBdsVyHKqu0hh2\nF9XrXsXYq7fZptA36Yk9soTdJ3fSXdOd9Cl/ZnLfu802vhBCdFWtFuzc3FzOnDnDzp07KSkpIT4+\nnp07dwKg1+tJT0/nwIEDODk58cgjj5Cfn09JSQmurq7s2LGDU6dOsXz5cnbv3g3AmjVrGDRokGVT\niQ7ncOE82qefQHPoAEatjup1r1L/20izddUAxVe+ZP7+SE5WnGC07y28PmU7Abo+ZhtfCCG6slYL\ndnZ2NuHh4QAEBgZy9epV9Ho9Wq0WtVqNWq1u6Zrr6urw8PBgxowZTJ8+HQAvLy8qKystm0J0HkVB\ns/MNtM8uM3XVd4RRvSEFY+8As06zs/gN4o4updZQy8KRj7Fi3PM4OzqbdQ4hhOjKWi3Y5eXlBAUF\ntbz28vKirKwMrVaLRqMhOjqa8PBwNBoN06ZNo1+/fj/4/Pbt21uKN0BycjIVFRUEBgYSHx+Pi4vL\nNef29HTDycmxPblumI+PzqLjd0Vmy3z+PCxcCO++C1otpKXh/OijeJuxq65rqiPm/RjS89LppunG\n7vt2M3PYzDaPY4/rDPaZWzLbD3vL3eardBRFafmzXq8nLS2Nffv2odVqmTNnDsXFxQwZMgQwnd8u\nKipiy5YtAERGRjJ48GD69OlDYmIiGRkZREVFXXOuiorath5em/j46OzuDlhmyawoaHbvRJsQi0Nl\nJY2332nqqgP6QLnePAcKlFSeImr/HP75bSEjeoxi65Tt9PPo3+bjt8d1BvvMLZnthy3nvtYvIq3e\nOMXX15fy8vKW15cvX8bnu0celpSUEBAQgJeXF87OzoSEhFBYWAjArl27yMrKIjU1FbVaDUBERAR9\n+pjOOU6aNImTJ0/+vFSiw6kuXaLbnAfpFr0AVWMT1X9Yz9Xd75iKtRn97dRbhO+ayD+/LWRuUBR/\n/9VB+nn0N+scQghhTVot2BMmTGD//v0AFBUV4evri1arBaBXr16UlJRQX18PQGFhIX379uXs2bNk\nZmaSkpKCRqMBTJ353LlzqaqqAiAnJ4eBAwdaJJSwAEVB89abeN0xBs2+v9N42x1cOZJN/dwos15Y\n1tDcwLKjT7Pg4DwURWFLRDp/mLgeF6drnzoRQgh70OqW+OjRowkKCmL27NmoVCoSExPZs2cPOp2O\niIgIoqKiiIyMxNHRkeDgYEJCQli3bh2VlZUsWLCgZZz09HRmzZrF3LlzcXV1xc/Pj5iYGIuGE+ah\nunwZXewSNO/9L4qbG9VrXqZ+3nxwMO+dbc9Ufc38/XMoKMtjqNcwtk75MwM95RsFQggBoFL+86R0\nF2Pp8xNd/RzIsQvZPP/JCtzU7oT6j2VMz7Hc4heC1rn9F1q0KbOioHlnD9plT+Nw5QqN4yZQvWET\nxn7m35p+/6u/E/PBIqoar/KbIQ+x5vaXcVO7mWXsrr7OlmKPuSWz/bDl3Nc6hy23huqCDEYDrxx/\nkfWfvYSiKCgoHP3mMAAOKgeCvEcwxj+UMT3HEuo/jl9oe5n9GFRlZejilqJ59x0UV1f0SS9SF7XQ\n7F11U3MTLxxLZEtBCq5OrmwMS+U3Qx8y6xxCCGELpGB3MaVVZ1h8aD6fXswhQNeH1PCtDOg+kE8v\n5pB78Ri5F46Rf/kffFFeQPoXrwHQWxvAGP9Qbu05ljH+YxnmFYSjQ/u/Due89210cUtx+PZbmkLH\nUbUxFWP/QHNFbHGu+hsePTCX45dyGdB9IFun/Jlh3kGtf1AIIeyQFOwu5O1Tu/ndkaeobqzilwN+\nxUsTN+Ch6Q7A1H73MLXfPQDUG+opKMsn9+IxPr1wjNyLx9hzajd7TpnuJqdV6wjpeStjvivgo/1C\n0Kq1rc6vKi9Hu/x3uLyzx9RVv7CGukcXm72rBjh0Zj/RhxZQ0VDBrwbez8sTN/6srX4hhLB1UrC7\nAH1jNfEfx5JZnIGbkzvJkzbz68EPorrG1dcuTi6E+o8l1H8sBJuuwC+pPN3SgedePMaHZ7P48GwW\nAI4qR4J6jGBMz1AiBk9iiNuonzzVyvl/30EXtwSH8nKabg2lOjmV5kDzX8VvMBp4MTeJjf94BY2j\nhpcmbiBy2LxrZhVCCGEiBbuT5V36jEWHovjq6r+42SeYLRHp9O8+oE1jqFQqBngOZIDnQB4c+jAA\n5XXlpm307wp4weU8Pi/LZ+sXaQAE6Ppwa89Q7nAbwezXj+Lx3iEUFxf0q1ZTt2AxOJr/DnMXay6w\n8OAjZJ//P/p260f6lD8zwmeU2ecRQghbJAW7kxgVI5vyk1mT8zwGo4HHg59i2ZhnzXZ/7B6uPbi7\n3zTu7jcN+Pc2+j+r88g6/SGfXsyhee8ufv3uLvxqIDfAkU2LbsY/uIYxFz5mtF8I7mp3sxwLwNFv\nPmTRwSjK68qY3v9/2BCWQjeNh9nGF0IIWycFuxNc0J/n8Q8W8tG5I/i59STlrjQmBoRZdM7vt9Gn\nj4zgkR6z0MbH4rJnFwa1E2/8dgQrb6niVNUxyD0GmLbRh/cYyZieoYT6j2OM/1h6uvu3ed5mYzPr\nP3uJlz5dg5ODE0m3vcj8EYtkC1wIIdpICnYHe/+rv7PkcDRX6q8wte89rA/bhLerd8cdwN69eD66\nAMfLl2gafQvVyVuIGDSYCKCstuwHV6MXlOVRUJbH61+Y7gXfR3cTt/YMZcx33wkf4jX0ulejl9WW\n8dih+Rz55jC9tQG8PuVP3OJ3awcFFUII2yI3TumgL97XGepY+UkCfyzcioujCysnJDEvaH6HdZqq\nygq0CXG47MpEcXamJjaBusdiwOnav7PVG+rJL8sznQe/kM2nF3OoaKhoeV/n3I1be45puRo92PeW\nlm30Y+c/YcHBeVysucDkm6by6l1b8HTxsnjO/8aWb7BwPfaYWzLbD1vOLTdO6URF5YUsOvgIJyqK\nGeo1jC0R2xjqPazD5nc+8D7ap5/E8dJFCAmhYt0mmocMbfVzLk4ujPUfx1j/ccASjIqR0xWnTB34\nd114VukhskoPAaZt9BE9RhLYfSB/O/0WACvGPU/0zU/goDL/V8OEEMKeSMG2IEVRSP8ijVXZK2ho\nbmD+iIWsGPc8rk6uHTK/6mol2meX4bLzDRS1mpr453BftYLmirp2jeegcmCQ12AGeQ3moWFzALhc\ne/kHV6N/XpZPflkePd39eW3yn74r9kIIIX4uKdgWUl5XzpNZizl4Zj/eLt6kT/kzk/ve3WHzO39w\nAO3SJ3C8cJ6mUcFUJ2+meegw3K+zBd4evm6+TOt/L9P63wuYtv5PXPmSwO4D0Dl3M+tcQghhz6Rg\nW8Dh0g+IyVrE5dpLTOwdRspdafi59+yQuVVVV3FfsRzXHX81ddXLnqU2Zgl890xyS3N1cuVm39Ed\nMpcQQtgTKdhm1NjcyOqc50nNT0btoGbl+CQWjYrusPO36qxD6JbG4Hj+HE3DR1L96haag4Z3yNxC\nCCEsSwq2mZyuOMWiQ1F8XpZPf49A0iK2Mco3uEPmVlVX4Z6YgOtft6M4OVETG0/tk093WFcthBDC\n8qRg/0yKovDGl38h4eNYag21/HZoJC/ctvaGHrZhDuoPs9AteRzHc99gGDacqle30DxiZIfMLYQQ\nouNIwf4ZKusr+N2Rp9hb8jYemu5snbSZGQPu65C5Vfpq3BOfxfUvf0RxdKTm6ThqlzwDzua5takQ\nQoiuRQp2Ox07/wmLD83nnP4bQv3HsTl8K711AR0yt/roh6au+mwphqFBVL+6GcPImztkbiGEEJ1D\nCnYbGYwGXj6+lg2fvYwKFXFjEnhy9NM4OXTAX6Vej/b5Fbj+Kd3UVS99htqlcdJVCyGEHZCC3QZn\nqr5m8cH5HL+US4CuD5vD0xnjH9ohc6s/PoruqWgcS89gGDKU6uTNGG6Wr08JIYS9kIJ9g/ac2sUz\nR5ZQ3VjFfQNm8oeJ6/HQdLf8xHo92t8n4rrtdRQHB2qffJqa3y0DjcbycwshhOgypGC3Qt9YzbKP\nfsebJ3bgrtby6qQtzBr8mw55aIf6k4/RPfkYjme+xjBosKmrHh1i8XmFEEJ0PVKwr+Mfl46z6GAU\nX1d9xc0+wWyZvI3+HoGWn7imBvfVq3B7fYupq378KWpi48HFxfJzCyGE6JKkYP8XRsVISt4G1ub+\nnmZjM08ELyV2TDzOjpa/uEt97BN0TyzG8euvMAwcZOqqb5FnSAshhL2Tgv0jF/TnefyDhXx07gg9\n3f1JuSuNO3rfafmJa2txX/M8rq9tNr2MftLUVbt2zJO9hBBCdG1SsP/De/96lyWHo6loqGBq33tY\nH7YJb1dvi8/rlHMM3ZOLcfpXCYbAAVRv3IxhTMdcfS6EEMI6SMEGaptqSfwkge1F6bg4uvDiHeuY\nGxRl+QvL6upwX/MCrmmbTMex6HFqlq+QrloIIcRP2H3BLiovZNHBRzhRUcxQryDSJm9jiNdQi8/r\n9GkOuicW41RyGkO//lQnb8EQOtbi8wohhLBOHfPcxy5IURSSc5KZ+lYYJyqKeXTEIvbff9jyxbq+\nHvdVK+h+7xQc/1VC7cLHqDj8iRRrIYQQ12WXHXZZbRlPZi3mUOkBvF282TblL0T0nWrxeZ0++9TU\nVZ86SXPfflQnb6Zp7HiLzyuEEML62V3Bzio9RMwHiyiru8zkwMm8clsKfu49LTtpfT3uL63BddNG\nVEYjtfMXUpOwEtzdLTuvEEIIm3FDBXv16tUUFBSgUqmIj49n5Mh/P285IyODvXv34uDgwPDhw0lI\nSMBgMJCQkEBpaSnNzc3ExsYSEhJCcXExK1euBGDw4MGsWrXKIqH+G0VRWJW9gtT8ZNQOalaNX82z\n4XF8W15j0Xmd8j4zddUnimm+qS/VG1NpGn+bRecUQghhe1o9h52bm8uZM2fYuXMnSUlJJCUltbyn\n1+tJT08nIyODHTt2UFJSQn5+Pu+88w6urq7s2LGDpKQk1q5dC0BSUhLx8fFkZmai1+s5cuSI5ZL9\nyKmKk6TmJxPYfQDvz/yAxTc/joPKgqfwGxpwW/083e8Jx+lEMXWPPMqVw59IsRZCCNEurXbY2dnZ\nhIeHAxAYGMjVq1fR6/VotVrUajVqtZra2lrc3Nyoq6vDw8ODGTNmMH36dAC8vLyorKyksbGRc+fO\ntXTnYWFhZGdnM3HiRAvG+7eBnoPYNzOLIV7DcFO7WXQup4I8U1f95T9p7nMT1Rs20XTbHRadUwgh\nhG1rtWCXl5cTFBTU8trLy4uysjK0Wi0ajYbo6GjCw8PRaDRMmzaNfv36/eDz27dvZ/r06VRUVNCt\nW7eWn3t7e1NWVnbduT093XBycmxrpmua4hv2k5/5+OjMNj6NjfDCC7BmDTQ3w+LFOL74It11ZpzD\nDMya2UrYY2awz9yS2X7YW+42X3SmKErLn/V6PWlpaezbtw+tVsucOXMoLi5myJAhgOn8dlFREVu2\nbOHKlSvXHOdaKipq23p4beLjo6OsrNosYzl9no8uZjFOXxbR3DvA1FXfcSfUA/XmmcMczJnZWthj\nZrDP3JLZfthy7mv9ItLqSVxfX1/Ky8tbXl++fBkfHx8ASkpKCAgIwMvLC2dnZ0JCQigsLARg165d\nZGVlkZqailqtbtka/96lS5fw9fX9WaG6hMZG3F5MovvUSTh9WUTdw/OoOJJtKtZCCCGEmbRasCdM\nmMD+/fsBKCoqwtfXF61WC0CvXr0oKSmhvr4egMLCQvr27cvZs2fJzMwkJSUFjUYDgFqtpn///hw/\nfhyAAwcOcPvtt1skVEdxLPwCzylhuL/yIka/nlTufBv9KxtRdN1a/7AQQgjRBq1uiY8ePZqgoCBm\nz56NSqUiMTGRPXv2oNPpiIiIICoqisjISBwdHQkODiYkJIR169ZRWVnJggULWsZJT08nPj6e5557\nDqPRyKhRoxg/3kpvGtLUhNuGl3Fb/xIqg4G6h+ZQs/L3KN08OvvIhBBC2CiVciMnkzuJpc9PtOcc\niGNRIbonFqP+ooDmX/Siet2rNE0Kt9ARmp8tn/e5FnvMDPaZWzLbD1vO3e5z2OI7TU24rfsDnpMn\nov6igLoHH6bi6DGrKtZCCCGsl93dmrQ9HL/8p6mrLsijuac/+nXJNIZP6ezDEkIIYUekw74egwG3\nDS/jGXEH6oI86mf/loqPcqRYCyGE6HDSYV+D44lidDELUefn0ezX09RVR1j+iV5CCCHEfyMd9o8Z\nDLgmr8fzrttQ5+dR/8BsU1ctxVoIIUQnkg77PziePIHuiUWo//EZzb5+6F/eSOPUezr7sIQQQgjp\nsAFobsY1ZaOpq/7HZ9TPnGXqqqVYCyGE6CLsvsN2PH3KdAX48VyMPXyoSttI4z3TO/uwhBBCiB+w\n3w67uRleeQXPSRNQH8+l/r6ZXPkoV4q1EEKILskuO2zHklPonngMPs1B6dGDqtStNE6f0dmHJYQQ\nQlyTfXXYRiOuaZvwDJuA+tMcmDWLK0dzpVgLIYTo8uynw66txeM3M3HO/j+M3t5UpaThERWJYqP3\nohVCCGFb7KZgO5RdRl2QR8O9v6R67Sso3z3TWwghhLAGdlOwjTf1pfzUWVCrO/tQhBBCiDazr3PY\nUqyFEEJYKfsq2EIIIYSVkoIthBBCWAEp2EIIIYQVkIIthBBCWAEp2EIIIYQVkIIthBBCWAEp2EII\nIYQVkIIthBBCWAEp2EIIIYQVkIIthBBCWAEp2EIIIYQVUCmKonT2QQghhBDi+qTDFkIIIayAFGwh\nhBDCCkjBFkIIIayAFGwhhBDCCkjBFkIIIayAFGwhhBDCCjh19gGY2+rVqykoKEClUhEfH8/IkSNb\n3svIyGDv3r04ODgwfPhwEhISMBgMJCQkUFpaSnNzM7GxsYSEhFBcXMzKlSsBGDx4MKtWreqkRK0z\nV+aHH36Y2tpa3NzcAIiLi2P48OGdFeu62pr522+/JS4ujoaGBpqamli+fDmjRo2yqnUG8+W25bX+\nXnl5OXfffTcpKSmEhoZa1VqbK7Mtr/OePXvYuHEjffr0AWD8+PEsXrzYqta5zRQbkpOToyxYsEBR\nFEU5ffq0MmvWrJb3qqurlbCwMKWpqUlRFEWZN2+ekpeXp+zevVtJTExUFEVRTp48qcycOVNRFEV5\n6KGHlIKCAkVRFGXp0qXKhx9+2IFJbpy5M584caJjA7RDezJv27ZN2bt3b8vn582bpyiK9ayzopg/\nt62u9feeeeYZ5b777lOOHTumKIr1rLW5M9vqOr/11lvK2rVrfzKWtaxze9jUlnh2djbh4eEABAYG\ncvXqVfR6PQBqtRq1Wk1tbS0Gg4G6ujo8PDyYMWMGy5cvB8DLy4vKykoaGxs5d+5cy294YWFhZGdn\nd06oVpgrszVpT+Z58+Zx7733AnDhwgX8/Pysap3BfLmtSXsyf/85d3d3Bg0aBGBVa22uzNakvZl/\nzJrWuT1saku8vLycoKCgltdeXl6UlZWh1WrRaDRER0cTHh6ORqNh2rRp9OvX7wef3759O9OnT6ei\nooJu3bq1/Nzb25uysrIOy9EW5sr8veTkZCoqKggMDCQ+Ph4XF5cOy3Kj2pu5rKyMRYsWUVNTw/bt\n261qncF8ub9nq2vd2NjIpk2bSE1NZfXq1QBWtdbmyvw9W13nvLw8cnNziYqKwmAwEBcXh7e3t9Ws\nc3vYVIf9Y8p/3HVVr9eTlpbGvn37+OCDDygoKKC4uLjl/YyMDIqKioiOjr7uOF3dz8kcGRlJbGws\nGRkZqFQqMjIyOvz42+NGM/v4+PDWW2+xfPnylh2Ga41jDX5Oblte69dee40HHnjgB/9xX2+cru7n\nZLbldR41ahQxMTGkp6fz1FNPERcXd91xbIFNddi+vr6Ul5e3vL58+TI+Pj4AlJSUEBAQgJeXFwAh\nISEUFhYyZMgQdu3aRVZWFqmpqajV6p9sE1+6dAlfX9+ODXODzJUZICIiomWcSZMm8d5773VgkhvX\nnsxVVVUMHjwYDw8PJk6cSGxsrFWtM5gvN9j2Wn/88ccYjUYyMjIoLS3l888/Z926dVaz1ubKvHHj\nRpte5/vvv5/AwEAAgoODuXLlCp6enlazzu1hUx32hAkT2L9/PwBFRUX4+vqi1WoB6NWrFyUlJdTX\n1wNQWFhI3759OXv2LJmZmaSkpKDRaADTOZP+/ftz/PhxAA4cOMDtt9/eCYlaZ67MiqIwd+5cqqqq\nAMjJyWHgwIGdkKh17cl84MAB3n77bQBOnDiBv7+/Va0zmC+3ra91ZmYmb775Jm+++SZ33nkniYmJ\nDBkyxGrW2lyZBwwYYNPr/Prrr/Puu+8CcPLkSby8vHB2draadW4Pm+qwR48eTVBQELNnz0alUpGY\nmMiePXvQ6XREREQQFRVFZGQkjo6OBAcHExIS0vKb94IFC1rGSU9PJz4+nueeew6j0cioUaMYP358\nJya7NnNmnjVrFnPnzsXV1RU/Pz9iYmI6Mdm1tSdz//79WbZsGQcPHqSxsbHlax/Wss5gvtwqlcqm\n1/parGWtzZXZ1te5d+/ePPPMM2RmZmIwGEhKSgKsZ53bQx6vKYQQQlgBm9oSF0IIIWyVFGwhhBDC\nCkjBFkIIIayAFGwhhBDCCkjBFkIIIayAFGwhhBDCCkjBFkIIIayAFGwhhBDCCvw/gyutcEYlgQYA\nAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "EPurg-tQSjMT",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ ""
+ ],
+ "execution_count": 0,
+ "outputs": []
+ }
+ ]
+}
\ No newline at end of file