From 0b6318836eee6fb32e50a3aadc2b9eaf3c36fedc Mon Sep 17 00:00:00 2001
From: Subham <40177225+loneWolf148@users.noreply.github.com>
Date: Mon, 18 Feb 2019 05:14:06 +0530
Subject: [PATCH] Created using Colaboratory
---
First_Date_with_TensorFlow.ipynb | 960 +++++++++++++++++++++++++++++++
1 file changed, 960 insertions(+)
create mode 100644 First_Date_with_TensorFlow.ipynb
diff --git a/First_Date_with_TensorFlow.ipynb b/First_Date_with_TensorFlow.ipynb
new file mode 100644
index 0000000..3a5ed89
--- /dev/null
+++ b/First_Date_with_TensorFlow.ipynb
@@ -0,0 +1,960 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "name": "First_Date_with_TensorFlow.ipynb",
+ "version": "0.3.2",
+ "provenance": [],
+ "include_colab_link": true
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ }
+ },
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ " "
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
\n",
+ "\n",
+ "You know what's important for understanding Deep Learning / Machine Learning?
\n",
+ "Intuition. Period.\n",
+ "\n",
+ "And Intuition comes when you run the code multiple times.\n",
+ "\n",
+ "So, today I can write a couple of defination and say this is this, this is that.
\n",
+ "You Google half of the things up. You find answers which you need to Google further.
\n",
+ "In the process, you probably won't even remember what's the first thing you started out with!\n",
+ "\n",
+ "So?\n",
+ "\n",
+ "Hence on, I will execute cells with code.
\n",
+ "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
+ "**No Theory Just Code.**\n",
+ "\n",
+ "I will at max give a defination that extends for a line. That's it.
\n",
+ "Let's get started!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "**RECOMMENDED!**
\n",
+ "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
+ "Don't just `shift+enter` the cells.\n",
+ "\n",
+ "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "gYWUpE-bYKWP",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Essential imports\n",
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "eKpz5NCIYMdi",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define some tensors\n",
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
+ " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "vmMcjzTxbWzw",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 67
+ },
+ "outputId": "9d023c64-7e70-4abb-a6da-aee9ca655aa2"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's print them out!\n",
+ "print (t1)\n",
+ "print (t2)\n",
+ "print (t3)"
+ ],
+ "execution_count": 29,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const_40:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_41:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_42:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "10ahnfjYbcop",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Where's Waldo?
\n",
+ "I mean, the value?
\n",
+ "\n",
+ "So, the thing is you can't print the value of tensors directly.
\n",
+ "You have to use `session`, so let's do that!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ol6O5I7Tb2nb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 202
+ },
+ "outputId": "7a96aeb0-ab9c-4dc0-ebc5-e16a02d85284"
+ },
+ "cell_type": "code",
+ "source": [
+ "sess = tf.Session()\n",
+ "print (sess.run(t1))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t2))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t3))\n",
+ "sess.close()"
+ ],
+ "execution_count": 30,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "rXKfVs_zb-kU",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Aaahaa!! Just printed those tensors!!!
\n",
+ "Feels good!
\n",
+ "\n",
+ "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
+ "And you are still using the markdown cells for the theory ?!\n",
+ "\n",
+ "I am just gonna say I am a unreasonable man.
\n",
+ "\n",
+ "\n",
+ "So, you are programming with tf.
\n",
+ "What ever you do is broken down to 2 basic steps:\n",
+ "- Building the computational Graph!\n",
+ "- Execute that graph using `session`!\n",
+ "\n",
+ "That's all!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Let's compare this 2 steps with what we did above!
\n",
+ "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
+ "And then I executed each tensor in this graph using a `session`.\n",
+ "\n",
+ "That simple!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Now, let's define a few more computational graphs and execute them with sessions.\n",
+ "\n",
+ "Okay, to start with let's build this computational graph!\n",
+ "\n",
+ "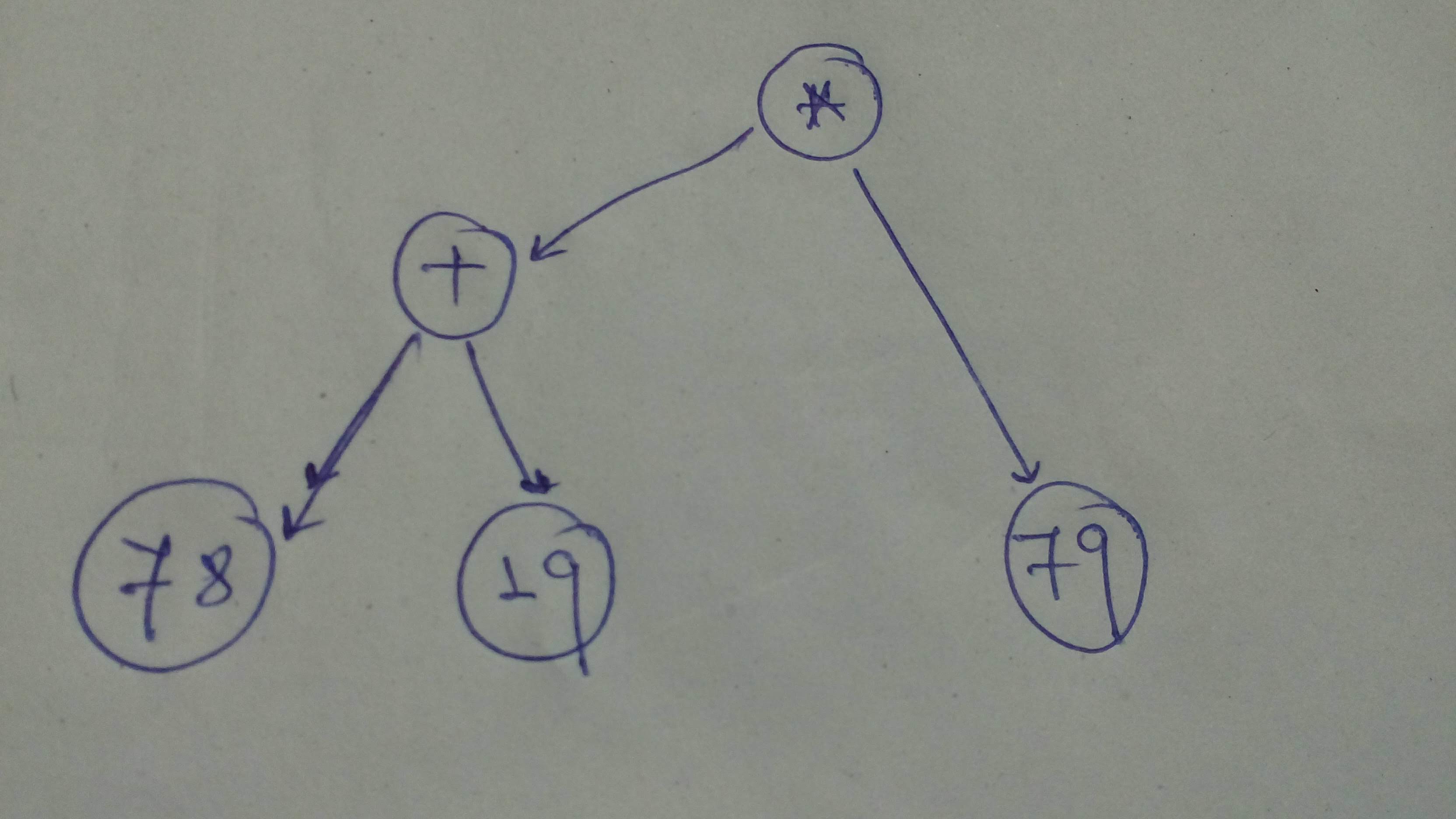"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "FyVz0GNqgreZ",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 50
+ },
+ "outputId": "c947d65c-a8ad-4dc8-82ac-cdd7a48a4787"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the graph\n",
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "\n",
+ "# Alternatively\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "\n",
+ "# Let's execute using session\n",
+ "sess = tf.Session()\n",
+ "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
+ "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
+ "sess.close()"
+ ],
+ "execution_count": 31,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "SVMMtuFYhaQB",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's define a sligtly more involved graph!\n",
+ "\n",
+ "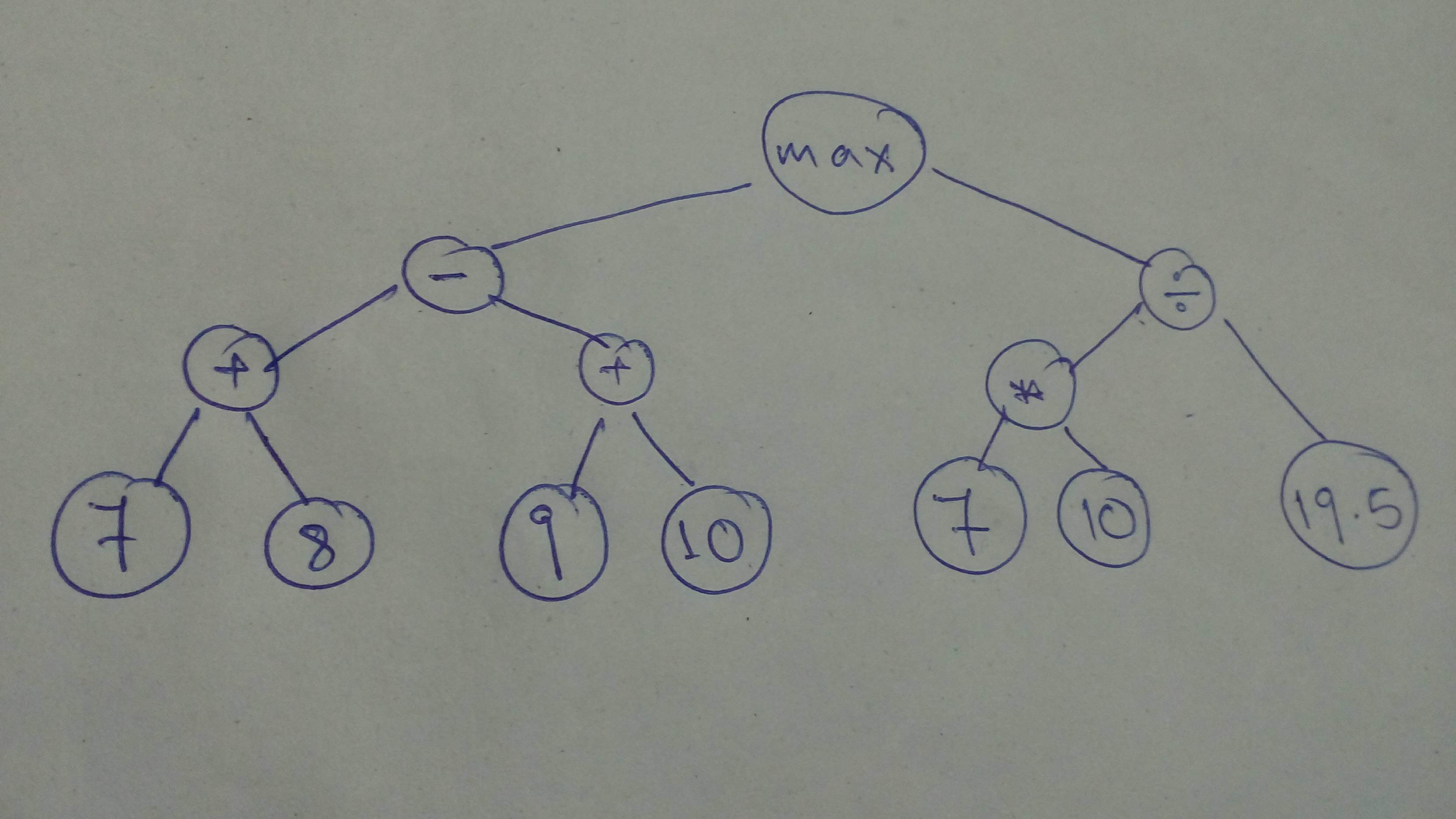"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4856BTvRhiBb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 67
+ },
+ "outputId": "d4e15bd2-fddb-4d11-cc84-493c113fa821"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let build the graph\n",
+ "# We need to cast cause the tensors operated on should be of the same type\n",
+ "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
+ " dtype=tf.float32)\n",
+ "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
+ "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "# Let's execute\n",
+ "sess = tf.Session()\n",
+ "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', part1_res)\n",
+ "print ('Part 2 Result: ', part2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 32,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "B-_ZDtEbj4N0",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Cool! Let's go! Build another graph and execute it with sessions.
\n",
+ "\n",
+ "But this time, it's all you!\n",
+ "\n",
+ "Build this graph and execute it with `session`!\n",
+ "\n",
+ "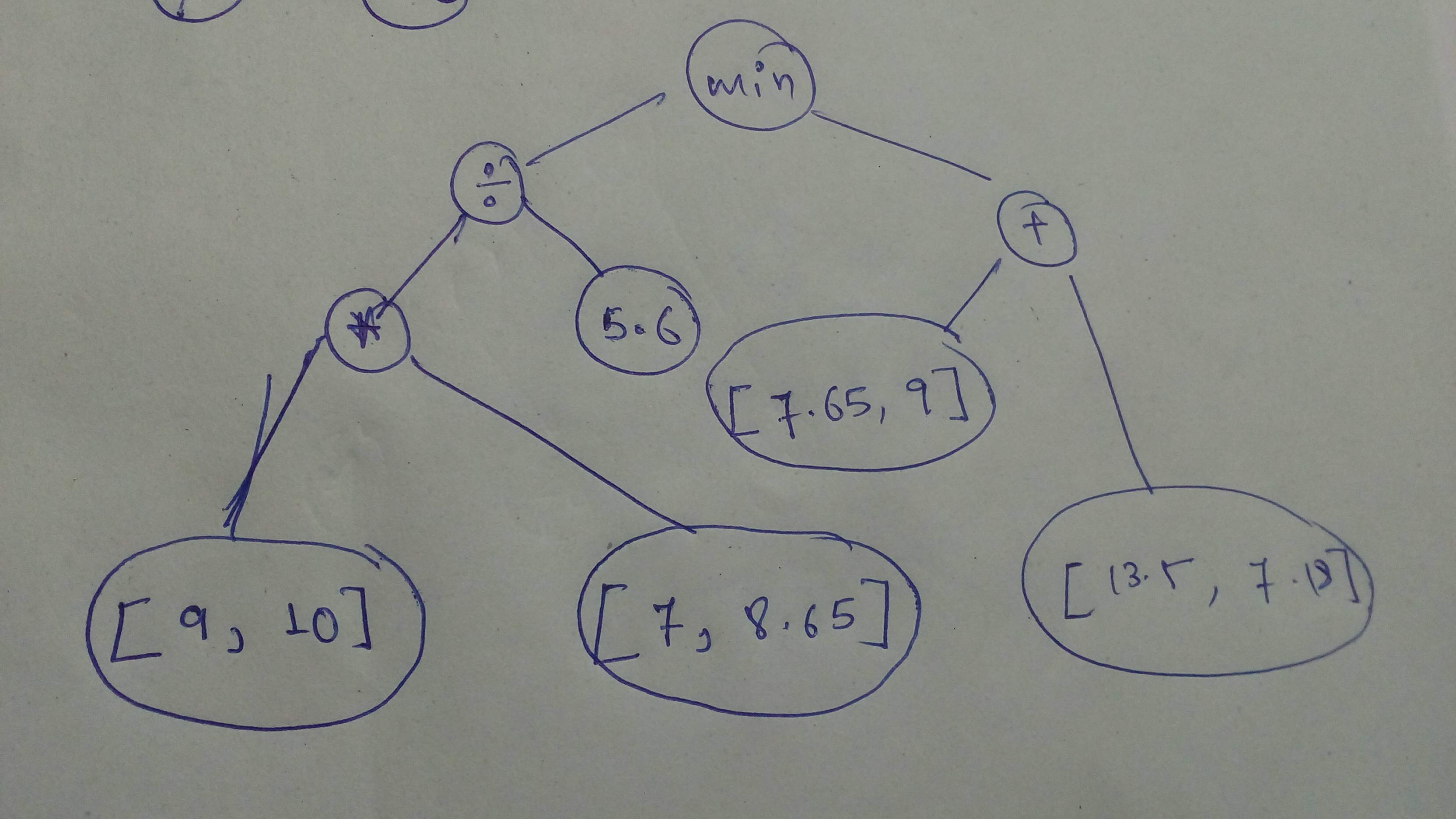\n",
+ "\n",
+ "_Remember that `tensors` operated on should be of the same type!_
\n",
+ "_Search up errors and other help you need on Google_"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "-uHNe1BolJY0",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 34
+ },
+ "outputId": "e3d4f048-ac4d-412c-bed2-03dce81f6dfa"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "mat1 = tf.constant([9,10],dtype=tf.float32,shape=(1,2))\n",
+ "mat2 = tf.constant([7,8.65],dtype=tf.float32,shape=(1,2))\n",
+ "mat3 = mat1 * mat2\n",
+ "val1 = tf.constant(5.6,dtype=tf.float32)\n",
+ "mat4 = mat3/val1\n",
+ "mat5 = tf.constant([7.65,9],dtype=tf.float32)\n",
+ "mat6 = tf.constant([13.5,7.19],dtype=tf.float32)\n",
+ "mat7 = mat5 + mat6\n",
+ "result = tf.minimum(mat4,mat7)\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess = tf.Session()\n",
+ "sess.run(result)"
+ ],
+ "execution_count": 33,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "array([[11.25 , 15.446429]], dtype=float32)"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 33
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "qmap38WelREN",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's do another!
\n",
+ "It's fun! Isn't it?!\n",
+ "\n",
+ "Build and execute this one!\n",
+ "\n",
+ "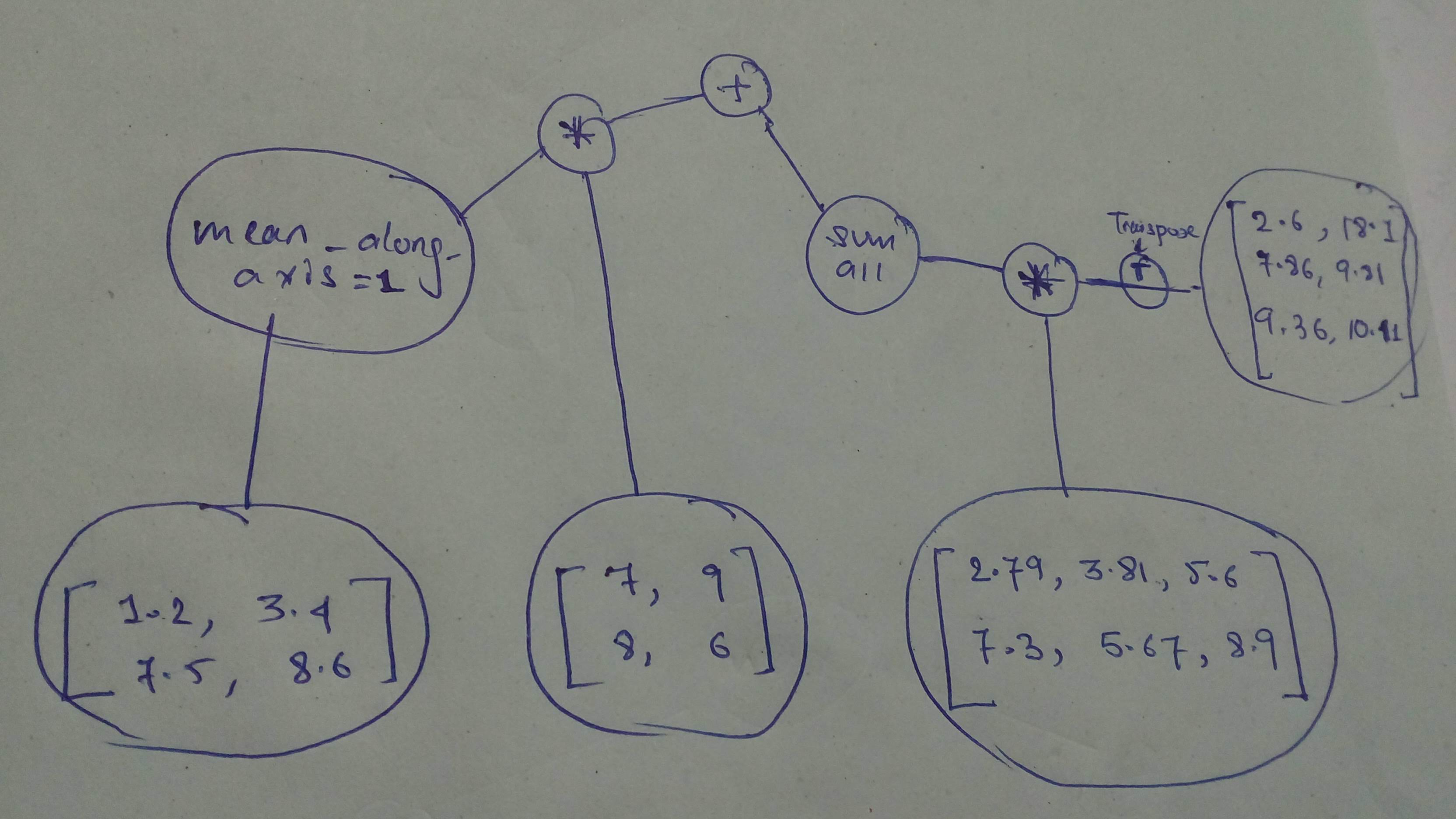"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "0ZhYwAlLmEvB",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 50
+ },
+ "outputId": "6e89c069-ee1a-477c-dd70-6e74c4a115f8"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "mat1 = tf.constant([[1.2,3.4],[7.5,8.6]],dtype=tf.float32,shape=(2,2))\n",
+ "mat1 = tf.reduce_mean(mat1,axis=1)\n",
+ "mat2 = tf.constant([[7,9],[8,6]],dtype=tf.float32,shape=(2,2))\n",
+ "mat3 = mat1 * mat2 \n",
+ "mat4 = tf.constant([[2.79,3.81,5.6],[7.3,5.67,8.9]],dtype=tf.float32,shape=(2,3))\n",
+ "mat5 = tf.constant([[2.6,18.1],[7.86,9.81],[9.36,10.41]],dtype=tf.float32,shape=(3,2))\n",
+ "mat5 = tf.matrix_transpose(mat5)\n",
+ "mat6 = mat4 * mat5\n",
+ "mat6 = tf.reduce_sum(mat6)\n",
+ "result = mat6 + mat3\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess = tf.Session()\n",
+ "sess.run(result)"
+ ],
+ "execution_count": 34,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "array([[386.1183 , 442.4683 ],\n",
+ " [388.41827, 418.3183 ]], dtype=float32)"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 34
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "BnB0b6qCmGmg",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "And a final one, before we move on to the next part!\n",
+ "\n",
+ ""
+ ]
+ },
+ {
+ "metadata": {
+ "id": "GQWyCvsQmMcL",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 84
+ },
+ "outputId": "f596dda2-10b2-4c8f-a068-8f02bdb5bab7"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
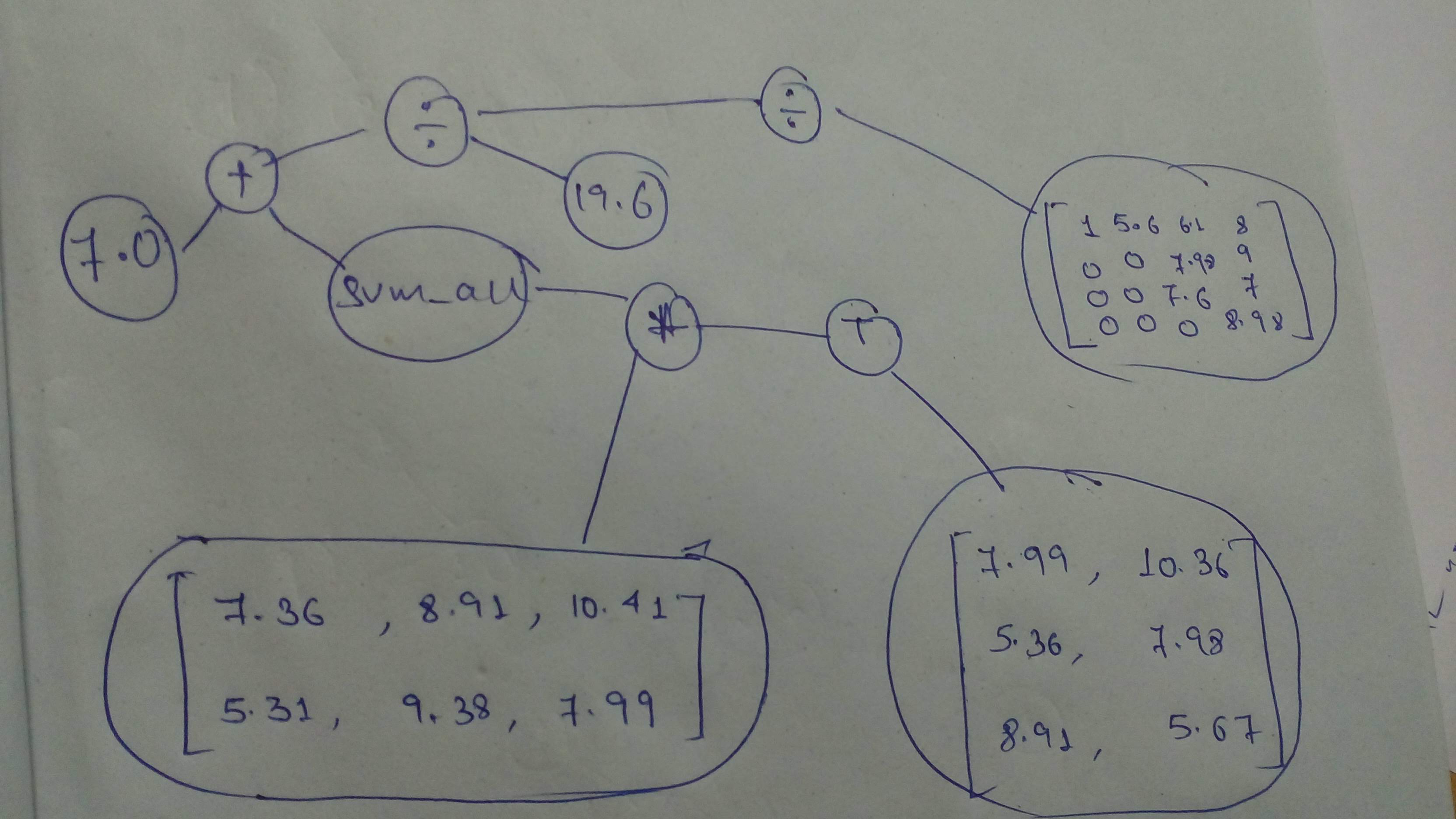
+ "mat1 = tf.constant([[7.99,10.36],[5.36,7.98],[8.91,5.64]],dtype=tf.float32,shape=(3,2))\n",
+ "mat1 = tf.matrix_transpose(mat1)\n",
+ "mat2 = tf.constant([[7.36,8.91,10.41],[5.31,9.38,7.99]])\n",
+ "mat3 = mat1 * mat2 \n",
+ "val1 = tf.reduce_sum(mat3)\n",
+ "val2 = tf.constant(7.0,dtype=tf.float32)\n",
+ "val3 = val1 + val2 \n",
+ "val4 = tf.constant(19.6,dtype=tf.float32)\n",
+ "val5 = val3 / val4 \n",
+ "mat4 = tf.constant([[1,5.6,6.1,8],[0,0,7.98,9],[0,0,7.6,7],[0,0,0,8.98]],dtype=tf.float32,shape=(4,4))\n",
+ "result = val5 / mat4\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess = tf.Session()\n",
+ "sess.run(result)"
+ ],
+ "execution_count": 35,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "array([[19.45126 , 3.4734392, 3.1887312, 2.4314075],\n",
+ " [ inf, inf, 2.4375012, 2.161251 ],\n",
+ " [ inf, inf, 2.5593762, 2.7787514],\n",
+ " [ inf, inf, inf, 2.1660647]], dtype=float32)"
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 35
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "12NC7XTPsJw7",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# Linear Regression\n",
+ "\n",
+ "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
+ "\n",
+ "\n",
+ "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hW31RZkjtNwI",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Create the dataset\n",
+ "X = np.linspace(-30.0, 300.0, 300)\n",
+ "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Normalize the dataset\n",
+ "X = X / np.max(X)\n",
+ "Y = Y / np.max(Y)\n",
+ "\n",
+ "# Divide it into train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "LQKy6U33y4lt",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the hyperparameters\n",
+ "learning_rate = 0.00001\n",
+ "n_epochs = 60\n",
+ "interval = 20"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "1h1-D8K1uT48",
+ "colab_type": "code",
+ "outputId": "c5055995-f859-46fc-ca3e-db6ad8fc428a",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 347
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# let's viz the first 10 datapoints of the dataset\n",
+ "plt.plot(train_X[:10], train_Y[:10], 'g')\n",
+ "plt.show()"
+ ],
+ "execution_count": 38,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFKCAYAAADmCN3IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3XlYVIX+P/D3zMCwg4CAmLupVIoL\nIAqhaeFCV7MClBIjaXFJLb0poUneNNDEjLQFl/SqaVJqRoiaEVkgiyRq5ZaZBgozCrIJMzDn94c2\nv8vXEBkHzizv1/Pc5z7MWeb98ZBvzzmzSARBEEBERERGSSp2ACIiItIdi5yIiMiIsciJiIiMGIuc\niIjIiLHIiYiIjBiLnIiIyIhZiB1AFwpFpd736exsi7KyGr3v15BxZvNgjjMD5jk3ZzZtbm4O//g4\nz8hvsbCQiR2hzXFm82COMwPmOTdnNk8sciIiIiPGIiciIjJiLHIiIiIjxiInIiIyYixyIiIiI6bT\n28/UajViYmJQXFwMmUyG+Ph4dO7cudE6e/fuxebNmyGVShEeHo6wsDCUlJQgNjYWKpUKGo0Gb7zx\nBvr27YuRI0eiQ4cOkMluvvpw5cqV8PDwuPfpiIiITJxORZ6amgpHR0ckJibixx9/RGJiIlavXq1d\nXlNTg7Vr1+KLL76ApaUlQkNDERwcjE2bNiE4OBiTJk1CQUEB3nvvPWzYsAEAsG7dOtjZ2elnKiIi\nIjOh06X17OxsBAcHAwACAgJQUFDQaHlhYSH69esHBwcHWFtbY9CgQSgoKICzszPKy8sBABUVFXB2\ndr7H+EREROZNpzNypVIJFxcXAIBUKoVEIoFKpYJcLr9tOQC4uLhAoVAgKioKoaGh2LNnD6qqqrB9\n+3btOnFxcSgqKoKPjw/mzZsHiURyL3MRERGZhWaLPCUlBSkpKY0eKywsbPSzIAh33Mffy9evX4+x\nY8di+vTpyMjIwPLly7FmzRrMnj0bQUFBcHJywsyZM7F//36MGTOmyf05O9u2yqf5NPXxd6aMM5sH\nc5wZMM+5ObP5abbIw8LCEBYW1uixmJgYKBQKeHl5Qa1WQxAE7dk4ALi7u0OpVGp/Li0txYABA3Dw\n4EG8+uqrAIDAwEAsWbIEADBhwgTtusOGDcOZM2fuWOSt8bm6bm4OrfIZ7oaMM5sHc5wZMM+5ObNh\nuF5Xjv0X9uHJ+0NhKbPU2371+lnrgYGBSE9PBwBkZGTA39+/0fL+/fvjxIkTqKioQHV1NQoKCuDr\n64uuXbtqz+aPHz+Orl27orKyEtHR0VCpVACAvLw89OrVS5dYREREoqqtr8Uz34ThlUMv46TyeJs8\np073yENCQpCVlYWIiAjI5XIkJCQAAJKTk+Hn54eBAwdi3rx5iI6OhkQiwcyZM+Hg4ICXX34ZCxcu\n1P4jYOHChXBwcMCwYcMwceJEWFlZ4cEHH7zj2TgREZEhEgQBr2bMRN6VHDx5/9MY4D6oTZ5XIjR3\ng9sAtcZlFEO8PNPaOLN5MMeZAfOcmzOL6928eLybFw9fj8HY9UQqrC2s9bp/fo0pERFRK/nyzE68\nmxePLg5dsXnsdr2X+J2wyImIiO5BzuUjmPPdDDjIHbHt8RS42bq16fOzyImIiHR04fofiNoXgQah\nARtG/xd9XLzaPINOL3YjIiIyd9fryvHsN2G4WnsV7w5fjUc6jxQlB8/IiYiIWkjdoMbU/VNwtvwM\npvV/Bc89NFW0LCxyIiKiFhAEATGH5+HwX99jTLcQxA19W9Q8LHIiIqIW+KhwDbb8ugl923vjw+D1\nkEn1/5HhLcEiJyIiuktp51OxJGsROth5YmvI57C3tBc7EouciIjobhxXHMOMb1+AjYUNtoZ8jo72\n94kdCQBftU5ERNSs4qoiTE6biBv1N7Bp7GfwdhsgdiQtnpETERHdQZW6CpPTJuJK9WXEBSzF2O6P\nix2pERY5ERFRExo0DZh+MBonlccR+eDzmN7/FbEj3YZFTkRE1IQl2W9i/4V9GNZpBBKCVkIikYgd\n6TYsciIion+w6eQGfFy4Br2d+2DD6M2wlFmKHekfsciJiIj+j4yLh/DG4X/D1doVW0N2wsmqndiR\nmsQiJyIi+h+nrv2GFw48BwupBTaP3YFuTt3FjnRHfPsZERHRLYoaBSZ/E45KVQU+Dt6AwZ7+Ykdq\nFs/IiYiIANyov4Ep+ybhYuWfmO8Xi6d6hYkd6a6wyImIyOwJgoBXv5uBoyV5eLpXOOb5LhA70l1j\nkRMRkdlbkfcOdp/7EoM7DMF7I9YY5NvMmsIiJyIis5ZyegcS85ejq2M3bBr7GawtrMWO1CIsciIi\nMltHirPwWsYrcJQ74bPHv0B7m/ZiR2oxFjkREZml89d/R1T6M9BAg41jtqCXc2+xI+mEbz8jIiKz\nU15bhsnfhONa7TUkPpKEYZ0eETuSznhGTkREZkXVoMLU/ZE4V34WMwfMQeSDUWJHuicsciIiMhuC\nIGDBD3PxY9EPGNv9X3hz6BKxI90zFjkREZmNtceSsO23/8LbbQA+fGwdpBLjr0Hjn4CIiOgupP6+\nF29nL4anXUdsDfkcdpZ2YkfSCxY5ERGZvGOlBZh56EXYWNhi6+M70cHOU+xIesNXrRMRkUkrqvwL\nk9Mmoq6hDv8dux392nuLHUmvWORERGSyqlSVmJw2EaU1JXg7MB6juo0VO5Le8dI6ERGZpAZNA14+\nOBW/XD2BqIei8ZL3DLEjtQoWORERmaS4rFgc/HM/Huk8Eu8EvWtUX4TSEjpdWler1YiJiUFxcTFk\nMhni4+PRuXPnRuvs3bsXmzdvhlQqRXh4OMLCwlBTU4OYmBgolUrY2NggISEBbm5uOHXqFN566y0A\nQJ8+fbBkifG/r4+IiMSz8eQ6JB//CH2cvbB+1GZYSE33TrJOZ+SpqalwdHTE9u3bMW3aNCQmJjZa\nXlNTg7Vr12LTpk3YsmULNm/ejPLycuzcuROdO3fGZ599hunTpyMpKQkAsGzZMsTGxmLHjh2oqqpC\nZmbmvU9GRERm6buLB7Hw8Hy0t3HDtsdT4GjlJHakVqVTkWdnZyM4OBgAEBAQgIKCgkbLCwsL0a9f\nPzg4OMDa2hqDBg1CQUEBLly4AG/vm68W9PX1xdGjR6FSqVBUVKR9fMSIEcjOzr6XmYiIyEz9dvVX\nvLA/ChZSC/x37HZ0cewqdqRWp1ORK5VKuLi43NyBVAqJRAKVSvWPywHAxcUFCoUCvXv31p5t5+bm\nori4GGVlZXB0dNSu6+rqCoVCodMwRERkvkprSjE5LRxV6kp8MPJj+HYYLHakNtHsTYOUlBSkpKQ0\neqywsLDRz4Ig3HEffy8PDQ3F6dOnERERgcGDBzcq+7vdFwA4O9vCwkLW7Hot5ebmoPd9GjrObB7M\ncWbAPOc215lvqG9g3FfP4lLlRbw94m28GBAldqw202yRh4WFISwsrNFjMTExUCgU8PLyglqthiAI\nkMvl2uXu7u5QKpXan0tLSzFgwADI5XLtC9mqq6tx6NAhuLi4oLy8XLtuSUkJ3N3d75iprKzm7qZr\nATc3BygUlXrfryHjzObBHGcGzHNuc525pPQ6XjrwPHKKchDWexJe8pptkn8OTf0jTadL64GBgUhP\nTwcAZGRkwN/fv9Hy/v3748SJE6ioqEB1dTUKCgrg6+uLzMxMrF69GsDNV7UHBQXB0tISPXr0QH5+\nPgDgwIEDCAoK0iUWERGZoeW5S7H3990Y4hmAVSM+MNm3mTVFp9fjh4SEICsrCxEREZDL5UhISAAA\nJCcnw8/PDwMHDsS8efMQHR0NiUSCmTNnwsHBAf7+/ti2bRvCw8Ph5OSEVatWAQBiY2OxePFiaDQa\n9O/fHwEBAfqbkIiITNbmY5vx3tGV6O7UA5vGboOVzErsSG1OItzNTWkD0xqXTMz1khRnNn3mODNg\nnnOb28zZxT8hdO942FraYd9Th3C/cy+xI7UqvV5aJyIiEtP58nOI2vcMBAj4dMxWky/xOzHdj7oh\nIiKTVFZ7Dc98E4ayujJsHL8RD983TOxIouIZORERGQ1VgwpT0yNx/vrvmD1wLp4f+LzYkUTHIici\nIqMgCAJez3wVPxUfxr96PIHYIYvFjmQQWORERGQUPvj5PWw/tRUD3AZizaOfQCphhQEsciIiMgJf\n/74HS4+8hfvsO2FLyOewtbQVO5LBYJETEZFBKyjJx8xvX4KdpT22huyEh10HsSMZFL5qnYiIDNal\nyouITJsElUaFrWO24KH2fcWOZHB4Rk5ERAbpwvU/MGFPCBQ3SvF2YDwe6zpa7EgGiWfkRERkcM6W\nncHTe8fhSvVlLBi8EC96Txc7ksFikRMRkUH5RXkSYV+Ph/KGEksC3sH0Aa+IHcmgsciJiMhgFJTk\nY1LqUyivK8eKYe8hqm+02JEMHouciIgMwpHiLDzzTRhq6qvxwciPMdHrGbEjGQUWORERie77S9/h\nuX0RUGvUSA7+FOPvf1LsSEaDRU5ERKLaf2EfotMjIZFIsGnMNozqNlbsSEaFbz8jIiLRfHVuF55P\nfxYWUgtsDdnJEtcBi5yIiESx49Q2vHxwKqxlNtgxbjeGdx4hdiSjxCInIqI29+nJ9Zj93XQ4yh3x\n5fi9GOI5VOxIRotFTkREberDYx9gwQ9z0d7GDbufSMNADx+xIxk1vtiNiIjahCAISMxfjhV578DT\nriO+HP817nfuJXYso8ciJyKiVicIAt4+Eoc1P69GF8du+HL8XnR17CZ2LJPAIiciolalETRY+ON8\nbDiRjJ7t7seX479GR/v7xI5lMljkRETUaho0DZj7/SxsP7UVD7g8hJTxX8Hd1l3sWCaFRU5ERK1C\n3aDGK4dewu5zX2KA20DsGLcLLtauYscyOSxyIiLSu7qGOrx4IArpf3yDwR2G4LPHU+Bo5SR2LJPE\nIiciIr2qUdcgKv0ZfH/pOwzrNAKbx34GO0s7sWOZLBY5ERHpTZWqEs+mhSO7+CeM6joG60f/F9YW\n1mLHMmn8QBgiIh2UVF/BkcvZEARB7CgGo7y2DKF7xyO7+CeM7/kkNo7ZyhJvAyxyIqIWUjWo8PTe\ncRi/ezRCdj2KjIuHzL7QlTeUeGrvOBSUHkV4nwh8HLwBcplc7FhmgUVORNRCHxeuxZmy0+jq2A1H\nS/IxMfVJjN8zBj8VHRY7miiuVF/GhD1jcVJ5HM89FI2kkR/BQso7t22FRU5E1AKXKi9iVf5ytLdx\nw8HQTBwKO4zR3cYi53I2nvzqcTz91TjkXs4RO2abuVR5EeN3j8GZstOY1v8VrBi2ClIJq6Ut8U+b\niKgFFv0Yg5r6GrwVsBTtrJ3Rz60/toR8jvSnv8OIzo/icFEm/rU7GJNSn8LPJUfFjtuqzpefw/jd\nY3Ch4g/M812AJQHLIJFIxI5ldljkRER36cCFfdj3RyqGdgxEWO9JjZYN8vDF5+N2Y++T+/HwfcPw\n3cVvMfrLEZiSNgknlSdEStx6Tl37DeP3jEVR1V9YNGQJFgxeyBIXiU43MdRqNWJiYlBcXAyZTIb4\n+Hh07ty50Tp79+7F5s2bIZVKER4ejrCwMNTU1CAmJgZKpRI2NjZISEiAm5sbIiMjUVNTA1tbWwDA\nggUL0Ldv33ufjohIT2rUNYg9PB8WUgssH7aqydIa4jkUu55IxeG/MpGQuxTpF9KQfiEN43pOwHy/\nWPRx8Wrj5Pp3XHEM4V9PwLXaa3jn4RV4wXua2JHMmk5FnpqaCkdHRyQmJuLHH39EYmIiVq9erV1e\nU1ODtWvX4osvvoClpSVCQ0MRHByMPXv2oHPnzkhKSkJ+fj6SkpLw9ttvAwDi4+PRu3dv/UxFRKRn\nSQWJuFj5J2YOmAMvlweaXT+o03A8fN8wZFz6Fgk5S/H173uQ+vtXeLJXKF73i0HPdsb59Z15V3IQ\nkRqKSlUFVo9Yi2ceiBQ7ktnT6dJ6dnY2goODAQABAQEoKChotLywsBD9+vWDg4MDrK2tMWjQIBQU\nFODChQvw9vYGAPj6+uLoUdO+f0REpuFc2Vms+fl9dLS7D/P8Ftz1dhKJBCO7BGN/6Pf479gdeNC1\nL3adTcHD2wdj9nfT8WfFhdYL3Qp+LPoBYXsnoFpdhY+C17PEDYROZ+RKpRIuLi4AAKlUColEApVK\nBblcfttyAHBxcYFCoUDv3r2RmZmJ0aNHIzc3F8XFxdp1kpKSUFZWhp49eyI2NhbW1k1/iICzsy0s\nLGS6RL8jNzcHve/T0HFm82COMwP6mVsQBDyTvgAqjQofPJ6E7h09ddpPpPtEPOsXhl2/7ULc93HY\ncWobvjjzOaYOmIpFwxahs1Pn5ndyF1rrWKefS8cz34RCI2jwRfgXmOA1oVWeRxfm+vv9t2aLPCUl\nBSkpKY0eKywsbPRzcx+E8Pfy0NBQnD59GhERERg8eLC27KdMmYI+ffqgS5cuiIuLw7Zt2xAdHd3k\n/srKapqL3WJubg5QKCr1vl9DxpnNgznODOhv7j1nv8S357/Fo12C8bDrY/e8z+Fuo3Ho6cew59yX\neDcvHskFydh0bBOmPPQ85gyaBw+7Djrvu7WO9Tfnv8ZLB6Igk8jw37E7EOj6qMH8TpnT73dT/2Bp\ntsjDwsIQFhbW6LGYmBgoFAp4eXlBrVZDEATt2TgAuLu7Q6lUan8uLS3FgAEDIJfLsWTJEgBAdXU1\nDh06BADay/QAMHLkSKSlpbVgNCKi1lGpqsCbP70BK5kV3gl6V2+vypZJZXi6dzieuP8pfHHmc6zM\nX471Jz7B1l834/m+L2LWoNfQ3qa9Xp7rXn15ZideOfQyrC1ssC1kJwLue1jsSPR/6HSPPDAwEOnp\n6QCAjIwM+Pv7N1rev39/nDhxAhUVFaiurkZBQQF8fX2RmZmpfVHc3r17ERQUBEEQEBUVhYqKCgBA\nTk4OevUyzheBEJFpWZEXj5KaK5gzaB66O/XQ+/4tpBaY5PUssiOOYuXw9+Fq0x4fFX4A3y39sOzI\nEpTVXtP7c7bE1l83Y8a3L8Je7oCUcXtY4gZKIujwAcENDQ1YtGgRLly4ALlcjoSEBHh6eiI5ORl+\nfn4YOHAg0tPTsWHDBkgkEkyePBnjx49HbW0tZs+ejfLycjg5OWHVqlVwcHBAWloa1q9fDxsbG3h4\neGDZsmWwsbFp8vlb4zKKOV2e+RtnNg/mODNw73OfVJ5AcMowdHHsisyJR9rkyz/qGuqw9ddNWH00\nESU1V+Agd8TL3jMwrf/Mu/oub30e6+TCD7Hopxi4Wrti57g96OfWXy/71Tdz+v1u6tK6TkUuNha5\nfnBm82COMwP3NrdG0GDc7tHIu5KDz/+1GyO6PKrndHd2o/4GNp3cgA9+XgXlDSXaWbXDjAGz8YL3\nNNhb2je5nb6O9ftHE7EsZwk8bDvgi/F7Dfq97+b0+91UkfOT3YiI/o8dp7Yh70oOxvd8ss1LHABs\nLGwwfcAryJ18HIuGvAUJJHgn5z/w29IPa39OQo1a/y/4BW6+MDk+5z9YlrMEnew746sn9xl0idNN\nLHIiov9xrfYq/pP9Juws7fF2YLyoWewt7TF70FzkR57AfL9YqDRqLMlehMHb+mPd8Y9QW1+rt+cS\nBAGLf3oD7x1die5OPfDVk/vQw6mn3vZPrYdFTkT0P5YdWYJrtdcw3y8WnvYdxY4DAHCQO+LffjE4\nOvkEXvP5N6rV1Vj44wIM2TYQm05ugKpBdU/71wga/DvzVXxy/EP0cfbC3gnp6OzQRU/pqbWxyImI\nbsm/kostv27CAy4P4oV+L4sd5zbtrJ3xhv9i5E8+gZkD5qCs7hrm//AaAj7zwWe/bUG9pr7F+6zX\n1OOVQy9jy6+fom97b+yekHZP72WntsciJyLCzUKb/8NcAMDy4e/BUmYpcqKmudq4Ii7gbeROPo6X\nvKejpOYKXs2YiQfWPoCU0zvQoGm4q/2oGlR46cDz+OLM5/Dx8MPuJ1IN5v3rdPdY5EREAD49uQ4n\nlccxyetZDPEcKnacu+Jh64GlDy9HzrPHEPVQNP4s/xMzD72E4Z8Pwd5zu6ERNE1ue6P+BqL2PYPU\n818hsGMQUsbtgZNVuzZMT/rCIicis1dSfQXxOUvRzqodFg99W+w4LdbR/j6sGP4ezsw6g2e8IvF7\n+Tm8cOA5jNz5MPb98c1tH6Ndpa7C5G/C8e3FAxjZ5TFsezwF9nLz/rxyY8YiJyKzF5e1EFXqSiwc\n8pZRX1ru1q4bVo9ci5+eyUdY70k4de1XPLcvAqO/eASH/jwAQRBQUXcdE79+EoeLMhHSfRw2j90O\nW0tbsaPTPdDp28+IiEzF4b8ysetsCga5+2DyA8+JHUcvejj1xNrHkjFn0DyszI/HnnO7EPFNKHw9\nBkOlUeG44hie6hWKD0Z+YtCvBaC7wzNyIjJbqgYVFvwwF1KJFMuHrYJMqv+vRxZTb5c+SB61CRnh\nWRjb/V/IL8nFccUxPPvAFKx9dB1L3ETwjJyIzNZHxz7AufKziO73Evq7DxQ7Tqt5qH1fbB77GY4r\njuFs2Rk82SsUUgnP40wFi5yIzNLFij+x6ugKuNm4I2bwIrHjtAlvtwHwdhsgdgzSMxY5EZmlRT8u\nwI36G0h8JIlvuyKjxmsrRGR20v9IQ/qFNAR2DMLTvcLFjkN0T1jkRGRWatQ1WPjjfFhILZAwLBES\niUTsSET3hEVORGZl9dGVuFR5EdP7z+JXdJJJYJETkdk4W3YGa4+9j/vsO2Gu73yx4xDpBYuciMyC\nIAiI+WEe1Bo1lj28AnaWdmJHItILFjkRmYU9577E4aJMBHcdjbHdHxc7DpHesMiJyORV1F3Hmz+9\nAWuZNZY9vIIvcCOTwiInIpO3Iu8dlNaU4FWff6ObU3ex4xDpFYuciEzaCeVxrD/xCXo49cTMgXPE\njkOkdyxyIjJZGkGD+ZmvQSNokDAsEVYyK7EjEekdi5yITNZnv23B0ZI8TLj/KTzSeaTYcYhaBYuc\niEySskaJt7MXw97SAf8JjBc7DlGrYZETkUmK+TYGZXVlmD/4DXSw8xQ7DlGrYZETkcnJvZyDDT9v\nwIOuffFCv2lixyFqVSxyIjIp9Zp6zP/hNQDA8mGrYCHltzWTaWORE5FJ2XDiE/x69SSmDpgKf88h\nYschanUsciIyGVeqL2N57jtwtnLG8uDlYschahMsciIyGXE/xaJKXYlFQ5egvW17seMQtQkWORGZ\nhMxLGdh97kv4ePji2QemiB2HqM3o9CoQtVqNmJgYFBcXQyaTIT4+Hp07d260zvXr1zF37lzY2dkh\nKSnpjtudOnUKb731FgCgT58+WLJkyb1NRURmpa6hDjGH50EqkWLFsPcglfAchcyHTr/tqampcHR0\nxPbt2zFt2jQkJibetk5cXBx8fHzuartly5YhNjYWO3bsQFVVFTIzM3WJRURm6sOfk/B7+TlE930J\n/dz6ix2HqE3pVOTZ2dkIDg4GAAQEBKCgoOC2dZYuXXpbkf/TdiqVCkVFRfD29gYAjBgxAtnZ2brE\nIiIz9GfFBbx39F2423pgweCFYschanM6XVpXKpVwcXEBAEilUkgkEqhUKsjlcu069vb2d7WdUqmE\no6Ojdh1XV1coFApdYhGRmREEAbGHX0dtQy1WB66Fo5WT2JGI2lyzRZ6SkoKUlJRGjxUWFjb6WRAE\nnZ78n7a7m305O9vCwkKm03PeiZubg973aeg4s3kw1Zm/OvUVDv65HyO6jcBLQ5+HRCJptNxU574T\nzmx+mi3ysLAwhIWFNXosJiYGCoUCXl5eUKvVEASh0dl4U9zd3W/bzs3NDeXl5dp1SkpK4O7ufsf9\nlJXVNPtcLeXm5gCFolLv+zVknNk8mOrM1epqvPLNLFhKLfH2kBVQKqsaLTfVue+EM5u2pv7BotM9\n8sDAQKSnpwMAMjIy4O/vr/N2lpaW6NGjB/Lz8wEABw4cQFBQkC6xiMiMvJf/Lv6quoQZA2ajt0sf\nseMQiUane+QhISHIyspCREQE5HI5EhISAADJycnw8/ODt7c3oqKiUFFRgZKSEkRGRmLGjBlNbhcb\nG4vFixdDo9Ggf//+CAgI0N+ERGRyzlw7jQ8Lk9DZoQte83ld7DhEopIIut7gFlFrXEYxp8szf+PM\n5sHUZhYEAU/vHYcfi37Af8fuwJjuIf+4nqnNfTc4s2nT66V1IiKx7Dqbgh+LfsDobmObLHEic8Ii\nJyKjUVF3HYt/ioWNhQ2WPswvRSECWOREZEQScpdCcaMUr/m8jq6O3cSOQ2QQWOREZBSOK45h48l1\nuL9dL0wfMEvsOEQGg0VORAZPI2gwP/M1aAQNEoYlwkpmJXYkIoPBIicig7f1180oKD2Kp3qFYlin\nR8SOQ2RQWOREZNCUN5RYeiQO9pYOWBLwjthxiAwOi5yIDNrb2YtRXleOmMEL4WHXQew4RAaHRU5E\nBuvI5WxsP7UVD7n2w9R+L4kdh8ggsciJyCDVa+qxIHMuAGDF8FWwkOr0idJEJo9FTkQGaf2Jj/Hb\ntV8w+YHn4Nfh7r6YicgcsciJyOBcrirG8tx34GLtgkVD3xI7DpFB47UqIjI4i3+KRbW6CksD18DF\n2lXsOEQGjWfkRGRQMi4ewle/74Kvx2BEPDBZ7DhEBo9FTkQGo7a+FjGH50EqkWLF8PcglfCvKKLm\n8L8SIjIYa4+9jz+un8eL/aahb/t+YschMgosciIyCH9cP4/VR1fCw7YD5g+OFTsOkdFgkROR6ARB\nwMLD81HXUIf/BL4DB7mj2JGIjAZftU5ErUYjaFDXUIe6+lrUNdShtqEWqgYVahtqtY/VNdTh16u/\n4NuLBxDU6RFMuP9psWMTGRUWOZGJ+rtEy27Uo6Ra2WSJ/l20fy+va6hF7a3HtOs31KKu/n/Wv7WO\n6v+UdF19HVSaOtTW31xHrVHfdV5LqSWWByVCIpG04p8KkelhkRMZubqGOpxQFOJoSd6t/+XjSvXl\nFpWorqQSKaxl1rCSWUEus4KVhTXs5fawkllDLpPfXGZhBSuZNaxk8lv/bw1ri1vry6y06wz1DMT9\nzr1aPTORqWGRExkRQRDwV9Ul5F/J1Rb3CcVxqDQq7Tqu1q7wdhugLUhHW3tI6mW3ivNmif5z0Vrd\n+t//Fq01rG8VtHb9v7eRWsFoi6W5AAAbmElEQVRCasEzaCKRsciJDFi1uhqFpT8jX3u2nYfSmhLt\ncgupBfq69oNPBz/4ePjB12Mwujp2a1Subm4OUCgqxYhPRG2ARU5kIARBwO/l55BfkoujJfk4WpKH\n367+ggahQbtOR7v7MK7nBPh43Cxub7f+sLGwETE1EYmNRU4kkut15SgoOYqjJXnIL8lFQUk+yuvK\ntcutZdY3z7I7DL5V3L7oaH+fiImJyBCxyInaQIOmAaeu/fY/L0jLw5my043W6ebYHY92GQXfW5fJ\nH3TtC7lMLlJiIjIWLHKiVqCoUTQq7Z9LC1CtrtIut7O0R1CnR+Dr4QsfDz8M8vBDe5v2IiYmImPF\nIie6R6oGFX5Rnrh1ifxmcf9ZcaHROn2cvW5eHr91tt3H2QsyqUycwERkUljkRC0gCAKKq4oalfZx\nxTHUNdRp13G2csZjXUZpS3ug+yA4WbUTMTURmTIWOdEd1NbX4pjiZxy9knfr1eR5uFJ9WbtcJpHh\nQde+8Ll1idyvw2B0d+rJ91YTUZthkRM1QVGjwNgvR+Ji5Z/ax9xtPRDSfRx8OvjB18MP3m4DYGdp\nJ2JKIjJ3LHKif6ARNJh56EVcrPwTT/cKx5juIfDx8MN99p14tk1EBoVFTvQP1vy8Gt9f+g6PdRmF\ntY8lQyrhN/4SkWHSqcjVajViYmJQXFwMmUyG+Ph4dO7cudE6169fx9y5c2FnZ4ekpKQ7bhcZGYma\nmhrY2toCABYsWIC+ffve42hEusm5fATxOW+jg50nPnj0E5Y4ERk0nf6GSk1NhaOjI7Zv345p06Yh\nMTHxtnXi4uLg4+Nz19vFx8djy5Yt2LJlC0ucRHOt9iqmHZwKAQI+Cd4IVxtXsSMREd2RTkWenZ2N\n4OBgAEBAQAAKCgpuW2fp0qW3FfndbEckFkEQMOe7GSiq+gvz/WIxtGOg2JGIiJql06V1pVIJFxcX\nAIBUKoVEIoFKpYJc/v8/TtLe3v6utwOApKQklJWVoWfPnoiNjYW1tbUu0Yh0lnz8Q+y/sA9BnR7B\nnEHzxI5DRHRXmi3ylJQUpKSkNHqssLCw0c+CIOj05H9vN2XKFPTp0wddunRBXFwctm3bhujo6Ca3\nc3a2hYWF/j8Vy83NQe/7NHSc+aa8ojz8J3sx3O3csXPidnSwN60PcDHH4wyY59yc2fw0W+RhYWEI\nCwtr9FhMTAwUCgW8vLygVqshCEKjs/GmuLu7/+N2f19uB4CRI0ciLS3tjvspK6tp9rlayhy/s5kz\n31RRdx2hKeGo19Rj7ch1kN2wg+KG6fy5mONxBsxzbs5s2pr6B4tO98gDAwORnp4OAMjIyIC/v7/O\n2wmCgKioKFRUVAAAcnJy0KtXL11iEbWYIAh47ftZuFhxAa/6zMPwziPEjkRE1CI63SMPCQlBVlYW\nIiIiIJfLkZCQAABITk6Gn58fvL29teVcUlKCyMhIzJgx4x+3k0gkCA8PR1RUFGxsbODh4YFZs2bp\ndUiipmz+ZSO+/n0P/D2H4nW/WLHjEBG1mETQ9Qa3iFrjMoo5XZ75m7nPfFJ5AmO/HAk7Szt8F/4T\nOtrfJ3K61mGOxxkwz7k5s2lr6tI6P9mNzFKVugovHngOdQ112Dh6i8mWOBGZPn5kFZkdQRAwP/M1\n/F5+DtP7z0JwtzFiRyIi0hmLnMzO56c/wxdnPscgdx8sHBIndhwionvCIiez8qviV8T8MA+Ocid8\nMupTyGXNv22SiMiQ8R45mY0adQ0mfjURNfU12DB6C7o6dhM7EhHRPeMZOZmNN3+KwcnSk5ja90WM\n6/mE2HGIiPSCRU5mYdfZFGz5dRMGdBiAtwKWiR2HiEhveGmdTN758nOY9/0c2Fna4/PQz2Gt4Rfy\nEJHp4Bk5mbS6hjq8eOB5VKursHL4avR27S12JCIivWKRk0lbkrUIJ5SFePaBKXi6d7jYcYiI9I5F\nTibrm/NfY/2JT+Dl8gCWPbxC7DhERK2CRU4m6WLFn3g1YyZsLGywbtRm2Fraih2JiKhV8MVuZHLU\nDWq8fPB5XK8rx/sjPkQfFy+xIxERtRqekZPJeSfnPzhako/Q3hMxyetZseMQEbUqFjmZlG//3I+1\nx95Hz3b3Y8WwVZBIJGJHIiJqVSxyMhnFVUV45dDLsJJZIXnUJtjL//m7e4mITAnvkZNJqNfUY9rB\naFyrvYblw1ahX3tvsSMREbUJnpGTSViZn4Ajl7MwrucERD0ULXYcIqI2wyIno/fDX9/jvfx30cWx\nG1Y9ksT74kRkVljkZNRKakow/eALsJBaYF3wp3Cyaid2JCKiNsV75GS0GjQNmPHti1DcKMV/At/B\nQA8fsSMREbU5npGT0UoqWIXDf32PUV3H4GXvmWLHISISBYucjNKR4iwsz1uGjnb3IenRj3hfnIjM\nFoucjM7VG1fx8sGpkECCj0dthIu1q9iRiIhEwyIno6IRNJj93TRcri5GzOBFGOI5VOxIRESiYpGT\nUfm4cC0O/rkfwzuNwKxBr4kdh4hIdCxyMhpHS/Kw9Egc3G09sPaxdZBK+OtLRMS/CckolNeW4aUD\nz6NB04CPHlsPd1t3sSMRERkEFjkZPEEQ8Nr3s3Cp8iLm+s5HUKfhYkciIjIYLHIyeBtPrsM35/ci\noOPD+LdvjNhxiIgMCoucDNoJRSHifoqFq7UrPnpsPWRSmdiRiIgMCoucDFaVqhIvHHgOKo0Kax79\nBJ72HcWORERkcFjkZJAEQcC/M+fgj+vn8crAV/Fo11FiRyIiMkg6Fblarca8efMQERGByZMn49Kl\nS7etc/36dURHR2P27NmNHs/NzcXQoUORkZGhfezUqVOYNGkSJk2ahLi4OF0ikYn57Lct2HX2C/h4\n+OGNwW+KHYeIyGDpVOSpqalwdHTE9u3bMW3aNCQmJt62TlxcHHx8Gn8b1cWLF/Hpp59i0KBBjR5f\ntmwZYmNjsWPHDlRVVSEzM1OXWGQifrv6K2J/fB1OVu2QPOpTWMosxY5ERGSwdCry7OxsBAcHAwAC\nAgJQUFBw2zpLly69rcjd3NywZs0aODg4aB9TqVQoKiqCt7c3AGDEiBHIzs7WJRaZgGp1NV46EIUb\n9Tfw/ogP0dmhi9iRiIgMmk7fR65UKuHi4gIAkEqlkEgkUKlUkMvl2nXs7e1v287Gxua2x8rKyuDo\n6Kj92dXVFQqF4o7P7+xsCwsL/b962c3NofmVTIyhzRzz1as4XXYKswfPxnP+Ea3yHIY2c1swx5kB\n85ybM5ufZos8JSUFKSkpjR4rLCxs9LMgCHoLdDf7Kiur0dvz/c3NzQEKRaXe92vIDG3mlNM7sPHY\nRni7DcDrA99slWyGNnNbMMeZAfOcmzObtqb+wdJskYeFhSEsLKzRYzExMVAoFPDy8oJarYYgCI3O\nxlvCxcUF5eXl2p9LSkrg7s6P3zQ3v5efxeuZr8He0gHJoz6FlcxK7EhEREZBp3vkgYGBSE9PBwBk\nZGTA399f5wCWlpbo0aMH8vPzAQAHDhxAUFCQzvsj41NbX4sX9kehpr4aiY+8jx5OPcWORERkNHS6\nRx4SEoKsrCxERERALpcjISEBAJCcnAw/Pz94e3sjKioKFRUVKCkpQWRkJGbMmIG6ujps2LAB58+f\nxy+//IItW7Zg48aNiI2NxeLFi6HRaNC/f38EBATodUgybHFZsfjl6glEPvg8nuwVKnYcIiKjIhH0\neYO7jfDeqX4Ywsxf/74H0fun4AGXB5EemgEbi9tfEKlPhjBzWzPHmQHznJszm7am7pHzk91INBeu\n/4FXM16BrYUt1o3a3OolTkRkinS6tE50r1QNKrx88HlUqiqQNPIj9HbpI3YkIiKjxDNyEsXSI2/h\n59IChPeJwCSvZ8WOQ0RktFjk1Ob2X9iHjwvXoFe73kgYdvvH+xIR0d1jkVObKqr8C7MPTYO1zBrJ\nozbB3vL2TwAkIqK7x3vk1GbqNfV4+eBUlNWVYeXw9/FQ+75iRyIiMno8I6c2szx3GXKvHMGE+59C\n5INRYschIjIJLHJqEx8e+wDvFySim2N3JD6SBIlEInYkIiKTwEvr1KoEQUB8zttYXbASnnYdsTVk\nJxzkjs1vSEREd4VFTq1GI2gQ88M8bPplA7o79cAX4/fy+8WJiPSMRU6tQt2gxqzvXsaus1/gIdd+\n+Hzcbrjb8lvtiIj0jUVOelejrsEL+6fg24sHMLjDEGx7fCecrNqJHYuIyCSxyEmvKuquY3LaRBy5\nnIWRXR7DxtFbYWtpK3YsIiKTxSInvVHUKDAx9UmcVB7HhPufwppHkyGXycWORURk0vj2M9KLvyov\nYfye0TipPI4pD07FR49tYIkTEbUBnpHTPTtbdgZhe59AcXURZg+ci4VD4vg+cSKiNsIip3tSWPoz\nJqU+hau1V/Hm0P9g1sBXxY5ERGRWWOSks5+KDiMybRKq1VVIfCSJH7tKRCQCFjnpZP+FfXhh/xRo\nBA3WjdqE8fc/KXYkIiKzxBe7UYulnN6BqH3PQCaRYUvI5yxxIiIRscipRTac+AQzD70Ee7kDdo77\nCiO7PCZ2JCIis8ZL63RXBEHAqqMrsDx3Gdxs3LFz3B5+nzgRkQFgkVOzNIIGcT/F4pPjH6KLQ1fs\nHL8HPZx6ih2LiIjAIqdm1GvqMff7Wdhxahv6OHth57g98LTvKHYsIiK6hUVOTaqtr8XLB6di3x+p\nGOg+CNv/9SVcrF3FjkVERP+DRU7/qEpVief2PYPDRZkIum84No/9DPZyB7FjERHR/8Eip9tcq72K\niNSn8XNpAcZ2/xc+Cd4IawtrsWMREdE/YJFTI5erihH+9QScLjuFiX2ewXsj1sBCyl8TIiJDxfeR\nk9b5679j3O7ROF12Ci95T8f7Iz9kiRMRGTj+LU0AgF+UJxH+9QQobpRiweCFmOszn99gRkRkBFjk\nhNzLOXg2LQzX68rxzsMr8IL3NLEjERHRXWKRm7nvLn6LqemTUddQh7WPJiOszySxIxERUQvodI9c\nrVZj3rx5iIiIwOTJk3Hp0qXb1rl+/Tqio6Mxe/bsRo/n5uZi6NChyMjI0D4WGRmJp59+GpGRkYiM\njMTJkyd1iUUtlPJLCiLTJqJBaMCmsZ+xxImIjJBOZ+SpqalwdHREYmIifvzxRyQmJmL16tWN1omL\ni4OPjw9OnTqlfezixYv49NNPMWjQoNv2GR8fj969e+sSh3Sw9dfN+HfmHNha2GFLyA4E3hckdiQi\nItKBTmfk2dnZCA4OBgAEBASgoKDgtnWWLl0KHx+fRo+5ublhzZo1cHDgB4uIac3P72Pu97PgbO2M\nXU98zRInIjJiOp2RK5VKuLi4AACkUikkEglUKhXkcrl2HXt7+9u2s7GxaXKfSUlJKCsrQ8+ePREb\nGwtra34Aib4JgoBlR5Yg6edV6Gh3H7597iDao5PYsYiI6B40W+QpKSlISUlp9FhhYWGjnwVBuKcQ\nU6ZMQZ8+fdClSxfExcVh27ZtiI6ObnJ9Z2dbWFjI7uk5/4mbm+leKWjQNGBm2kx88vMn6OXSCwcj\nD6Jru65ixxKFKR/nppjjzIB5zs2ZzU+zRR4WFoawsLBGj8XExEChUMDLywtqtRqCIDQ6G2+pvy/T\nA8DIkSORlpZ2x/XLymp0fq6muLk5QKGo1Pt+DYGqQYVXDr2EPed2oW97b+z41y7Yqm9eUTHVmZti\nyse5KeY4M2Cec3Nm09bUP1h0ukceGBiI9PR0AEBGRgb8/f11DiYIAqKiolBRUQEAyMnJQa9evXTe\nHzVWo67Bc/sisOfcLvh7DsXuJ1LhbusudiwiItITne6Rh4SEICsrCxEREZDL5UhISAAAJCcnw8/P\nD97e3tpyLikpQWRkJGbMmIG6ujps2LAB58+fxy+//IItW7Zg48aNCA8PR1RUFGxsbODh4YFZs2bp\ndUhzdb2uHM9+E47cK0fwaJdgbBi9BbaWtmLHIiIiPZII93qDWwStcRnF1C7PlNaUYuLXT+KXqycw\n4f6nsObRZMhljW9/mNrMd4Mzmw9znJszmza9Xlonw3ap8iLG7R6FX66ewHMPReOjxzbcVuJERGQa\n+BGtJubMtdMI+/oJXK4uxpxB8xDrv5hffkJEZMJY5CbkWGkBJqU+hWu117B46Nt4ZeAcsSMREVEr\nY5GbiJ+KDmNy2kTcqK/Bqkc+wOQHnxM7EhERtQEWuQlI/yMNLx54DhpBg3WjNmFczwliRyIiojbC\nF7sZuZ2nt+P59Gchk8iwNWQnS5yIyMywyI3Y+uMf45VDL8Ne7oCU8V9hRJdHxY5ERERtjJfWjdCV\n6svYeGIdVheshJuNO3aO24OH2vcVOxYREYmARW7gBEHAufKzyLmcjSOXs3DkcjYuVlwAAHRx6Iqd\n4/egh1NPcUMSEZFoWOQGpl5TjxOKQuRcycaR4mzkXsmG8oZSu9zJqh1GdR2DwZ5DEeE1GW62biKm\nJSIisbHIRVajrsHRkrxbZ9zZyL+Si5r6au3yjnb34aleofD3DIC/51B4uTwAqYQvbSAioptY5G3s\nWu1V5Fw+gpzL2ci5nIVCxTHUa+q1y3s794G/ZwCGeA6Fv+dQdHbowk9mIyKiJrHIW9mlyos4Upx1\nq7yzcLrslHaZhdQC3u373yzujgEY3GEIXG1cRUxLRETGhkWuRxpBg9PXTuHI5SzkXL5Z3kVVf2mX\n21rYIqjTIxjiORRDPAMwyMMXdpZ2IiYmIiJjxyK/B6oGFQoVP+PI5WzkFGch98oRlNeVa5e7Wrsi\npPs4+HsOxRDPoejb3huWMksRExMRkalhkbdAlaoSeVdykXPrbWAFJfmobajVLu/i2A2juo29VdwB\nuL9dL97fJiKiVsUiv4PSmlLti9KOXM7GSeVxaAQNAEACCR5wfUh7mdzfcyg87TuKnJiIiMwNi/wW\nQRBw/vrvyL18BEeKs3DkchbOX/9du1wulcPXYzCGeAZgSMeh8OvgDyerdiImJiIiYpGjSl2F2MOv\n4/u/DuFK1RXt4w5yR4zs8tjN4vYMwAD3QbC2sBYxKRER0e3Mvsiv3biKXWdS4GLrgvE9n7z5/u2O\nAXjQ5SHIpDKx4xEREd2R2Rd5F8eu+OPFy/D0cIZSWSV2HCIiohbhZ30CsJRZ8tXlRERklFjkRERE\nRoxFTkREZMRY5EREREaMRU5ERGTEWORERERGjEVORERkxFjkRERERoxFTkREZMRY5EREREaMRU5E\nRGTEWORERERGTCIIgiB2CCIiItINz8iJiIiMGIuciIjIiLHIiYiIjBiLnIiIyIixyImIiIwYi5yI\niMiIWYgdoLWp1WrExMSguLgYMpkM8fHx6Ny5c6N1rl+/jrlz58LOzg5JSUl33O7UqVN46623AAB9\n+vTBkiVL2nqkZt3NzHv37sXmzZshlUoRHh6OsLAw1NTUICYmBkqlEjY2NkhISICbmxsiIyNRU1MD\nW1tbAMCCBQvQt29fMUZrkr5nNuXjXFJSgtjYWKhUKmg0Grzxxhvo27cvRo4ciQ4dOkAmkwEAVq5c\nCQ8PDzFGuyN9z52VlYVVq1ZBJpNh2LBhmDlzpkiTNU3XmT/66CNkZWUBADQaDZRKJfbv328Ux1rf\nMxvDcdaZYOJ27dolvPXWW4IgCMLhw4eFOXPm3LbOnDlzhLVr1wqzZs1qdrvJkycLhYWFgiAIwty5\nc4Xvv/++tUdoseZmrq6uFkaNGiVUVFQIN27cEB5//HGhrKxM+PTTT4UVK1YIgiAIeXl5wqJFiwRB\nuDnz6dOn23aIFmqNmU31OCckJAjbt28XBEEQjh49KkydOlUQBEEYMWKEUFVV1bZD6EDfc48dO1Yo\nLi4WGhoahIiICOHs2bNtO9Bd0HXm/7uPdevWCYJgHMda3zMbw3HWlclfWs/OzkZwcDAAICAgAAUF\nBbets3TpUvj4+DS7nUqlQlFREby9vQEAI0aMQHZ2ditP0HLNzVxYWIh+/frBwcEB1tbWGDRoEAoK\nCnDhwgXtbL6+vjh69GibZ9eVPmc29ePs7OyM8vJyAEBFRQWcnZ3bPPu90Ofcly5dgpOTEzw9PSGV\nSjF8+HCTOtZ/q6+vx/bt2zF58uQ2zX0v9DmzsRxnXZn8pXWlUgkXFxcAgFQqhUQigUqlglwu165j\nb29/V9splUo4Ojpq13F1dYVCoWjlCVquuZn/dzkAuLi4QKFQoHfv3sjMzMTo0aORm5uL4uJi7TpJ\nSUkoKytDz549ERsbC2tr67Ydqhn6nLmsrMykj3NUVBRCQ0OxZ88eVFVVYfv27dp14uLiUFRUBB8f\nH8ybNw8SiaRth7oL+pxboVDctu6lS5fadqC7oOvMfztw4AAefvjhRv/dGvqx1ufMxnKcdWVSRZ6S\nkoKUlJRGjxUWFjb6WdDxE2n/aTtd96VP+pj57+WhoaE4ffo0IiIiMHjwYO0v/pQpU9CnTx906dIF\ncXFx2LZtG6Kjo/U4Rcu0xcwt2Vdb0OfM69evx9ixYzF9+nRkZGRg+fLlWLNmDWbPno2goCA4OTlh\n5syZ2L9/P8aMGaPfQVqoteeeOnWqfgPrgT5n/tuXX37Z6HUehnas22JmU2ZSRR4WFoawsLBGj8XE\nxEChUMDLywtqtRqCIDQ6G2+Ku7v7bdu5ublpL80BQElJCdzd3fU+R0voMrO7uzuUSqX259LSUgwY\nMAByuVz7i19dXY1Dhw4BgPbyFgCMHDkSaWlprTlSs1p7ZhcXF5M+zgcPHsSrr74KAAgMDNTOP2HC\nBO26w4YNw5kzZ0Qv8tae+/+ua2rHGgBqampw5coVdOrUSbvc0I51a89siMdZn0z+HnlgYCDS09MB\nABkZGfD399d5O0tLS/To0QP5+fkAbl66CQoKap3g96C5mfv3748TJ06goqIC1dXVKCgogK+vLzIz\nM7F69WoAN18NGhQUBEEQEBUVhYqKCgBATk4OevXq1bYD3QV9zmzqx7lr167as53jx4+ja9euqKys\nRHR0NFQqFQAgLy/PII8zoN+5O3XqhKqqKvz111+or69HRkYGAgMD23ym5ug6MwCcOnUKPXr00K5r\nLMdanzMby3HWlcl/+1lDQwMWLVqECxcuQC6XIyEhAZ6enkhOToafnx+8vb21RVVSUoJevXphxowZ\nGDx48D9ud+7cOSxevBgajQb9+/fHG2+8IfaIt2lu5oEDByI9PR0bNmyARCLB5MmTMX78eNTW1mL2\n7NkoLy+Hk5MTVq1aBQcHB6SlpWH9+vWwsbGBh4cHli1bBhsbG7HHbETfM5vycS4tLcXChQtRW1sL\nAFi4cCG8vLywefNm7NmzB1ZWVnjwwQfx5ptvGtx9U0D/c+fl5WHlypUAgFGjRol626gpus4MQPvW\nq/+9zGwMx1rfMxvDcdaVyRc5ERGRKTP5S+tERESmjEVORERkxFjkRERERoxFTkREZMRY5EREREaM\nRU5ERGTEWORERERGjEVORERkxP4fHSfF0cG5tQ0AAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jrsUps0nu8vj",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "** Question **
\n",
+ "Why did I created a session to plot the graph?
\n",
+ "[Ans]"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "P3-iuxE4sjAf",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the placeholders\n",
+ "\n",
+ "# Placeholders?\n",
+ "# The input to the model changes on iteration\n",
+ "# So we cannot have a constant in the input as we did before\n",
+ "# And thus we need placeholders which we can change on each \n",
+ "# iteration of the training\n",
+ "\n",
+ "x = tf.placeholder(tf.float32, name='x')\n",
+ "y = tf.placeholder(tf.float32, name='y')"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "8hPRkaoxvRyV",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the linear regression model\n",
+ "\n",
+ "# tf.Variable?\n",
+ "# We define the model parameters as tf.Variables\n",
+ "# as they get updated throghout the training.\n",
+ "# And variables denotes something which changes overtime.\n",
+ "\n",
+ "W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ "b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ "\n",
+ "pred_y = (W*x) + b"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "cSw1P8bkv96r",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the loss function\n",
+ "# We are going to use the mean squared loss\n",
+ "loss = tf.reduce_mean(tf.square(y - pred_y))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "5G4uQqjsygNj",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the optimizer\n",
+ "# And specify the which value (i.e. loss) it has to minimize\n",
+ "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "ttI7ZT-ozAm1",
+ "colab_type": "code",
+ "outputId": "9b616261-0cdc-49cf-ade6-24d94e2efa62",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 431
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# So the graph is now built\n",
+ "# Now let's execute the graph using session\n",
+ "# i.e. lets train the model\n",
+ "\n",
+ "# What it is to train a model?\n",
+ "# To update the paramters in the graph (i.e. tf.Variables)\n",
+ "# So that the loss is minimized\n",
+ "\n",
+ "# Okay let's start!\n",
+ "with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 43,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.32795018\n",
+ "Loss after epoch 20 is 0.3276611\n",
+ "Loss after epoch 40 is 0.3273722\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.22123063\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xd4VFX+P/D3nZnMpPeZkE56gEgT\nkID0BAsWllVERSxYsaz+dEWxgF8soOiubRWRdVlAxUXWvkRREKUJ0kyATHonvU0mybT7+2PCkCEJ\nCSHJTSbv1/PwTCb3zJ3zYUje3HvPPUcQRVEEERER9TmZ1B0gIiIarBjCREREEmEIExERSYQhTERE\nJBGGMBERkUQYwkRERBJR9PUblpfX9/Vb2vHxcUV1tV7SPvQ2R6+R9Q1sjl4f4Pg1sr4Lp1Z7tPv9\nQXckrFDIpe5Cr3P0GlnfwObo9QGOXyPr6zmDLoSJiIj6C4YwERGRRBjCREREEmEIExERSYQhTERE\nJBGGMBERkUQYwkRERBLp88k6+qO33/4b0tNPoqqqEk1NTQgKCoanpxdefvm1Htn/DTdcC40mADLZ\n2f/zvPPOBxe9319//RmXXTYJdXW1WL9+LZ588pmL3icREfUdhjCAhx9+DADw3XdfIzs7Cw899GiP\nv8eaNW/B1dW1R/f56aebMXbsePj5+TOAiYgGIIbweRw+fAiffroJer0eDz30GB5//CF8++2PAIBn\nn30S8+bNR3z8MLz88guor6+H2WzGo4/+FdHRMV3a/5w5s9rs78iR39HQoEN+fh6KigrxyCOPIzFx\nMrZv/xZbt26BIAhYsOBWGI1GnDiRiieeeARPPfUcXnjhWaxfvxGHDx/CRx+thSgKUKs1ePrp57Fj\nRwqOHz+Kmppq5Ofn4ZZbbsM118zttb83IiLqmn4Xwiv2Pouvs77o0X1eGzUXKya92K3XZmVl4pNP\ntkGpVLa7/bPPPsFll03CtdfORU5ONt58cw3+/vd/XEx3UVZWijVr3sL+/Xvx5ZefY9So0fjXvz7E\nhg2fwGAw4qWXlmPVqjfw4YfvY82at1BbW2N77Zo1r+Df/94AhcIdb7yxGj/8sB2CICArKxPvv/9P\nFBYWYPnyZQxhIqLW9HoosjIgz9ACni7ArDmAIPT62/a7EO5voqNjOgxgAPjjj+OoqalGSsp3AIDm\n5qZ22z3xxCO2a8Le3j548cXVHe5z5MjRAACNRgOdTofc3ByEhQ2FSuUMlcoZq1a90e7r6upqIQgC\nAgMDUV5ej7Fjx+Ho0cOIjY1HQsJIyOVyqNUaNDToulQ7EZGjEaoqIddqochIh1ybbn3MzICsIB+C\nKJ5tl5YFUa3u9f70uxBeMenFbh+19gYnJ6d2v28ymVq2K/DYY39FQsLI8+6ns2vCZ/YHAHL52cnD\nRVGETCaHKFq60FsBYqt/REajEYIga3efREQOy2KBrKgQ8ox0KDK0kGu1LV+nQ1ZZ2aa5WRMA4+Qp\nMMfEwhQbB4/kGX0SwEA/DOH+TBAENDVZj3S12nQAwPDhCdi9excSEkYiJycbBw7sxYIFC7u9v/aE\nhw9Ffn4e9Ho95HI5li59DH/727sQBBnMZrOtnaenJwRBQHFxMZycPHD06GGMHDnarg0RkcMwGCDP\nybYe0WZqIdemQ56hhSJTC0FvvxShKJPBEhaO5kvHwxwTB1NsHMwxsTDHxEL08rZr66H2APpo2V2G\n8AWYO/cG3Hvv7Rg6NBJxccMAADfccBNeemkFliy5GxaLBY8++sRF7a89Li4uWLz4fjz66BIAwE03\n3QJBEDBmzFgsWbIYzzyzwtb2ySefxeOPPw6LBQgODsGsWbPx/ff/617BRET9gKCrhzxD2xK2GS1h\nmw55TjaEcw4yRJUK5qgYmGJjYY6Jgzk2DqaYOJgjowBnZ4kq6Jgg9vG5yfI++t9FR9RqD8n70Nsc\nvUbWN7A5en2A49fYK/WJIoSyMus12oyW08ctp5HlJcVtmlu8vG2nj61hGwtTTBwsoWGA/OLWA+6N\n+tRqj3a/zyNhIiLqO2YzZPl5LQOjtJBnaqFoOY0sa3Wnh615UDAM02ZYwzY61nZkK6rVfTJ6ubcx\nhImIqOc1NkKenWUbhSzP0FoHSWVnQmiyv4tEVChgjog8Ozgqxhq25ugYiO7tH0E6CoYwERF1m1BT\nbXfLz5kjW1l+nt0tPwAgurrBFDfMOiAqNg6mliNbc0Qk0MGdKI6OIUxEROcnipCVFNvuq0VBDryO\np1rDtqK8TXOLvz+MEyfZXas1x8TCEhQMyLhuUGsMYSIisjIaIc/NaTUwqmUUckYGZOdM8uMkCLCE\nhqN51mj7UcgxMRB9/SQqYOBhCBMRDTYNDWfvq83Unh2FnJMNwWi0ayoqlTBHRcMQY71Ga46Ng+dl\nY1HhEwj08KI0gxFDGEBJSTEWLVqAuLh4AIDBYMCtt96OadNmXPC+Pv98C2pqajB16nTs3r0Lixff\n1267M8sQdjQjV2vZ2Zl4441X2yx/OG3aZbjkklG2535+fnjhhVcuuM/n2rlzB2bMSEJGRvp5ayCi\n/k2oqGhzrVaeoYW8sKBNW4unF0wjR1knsrAd2cbCEhYOKM6Jij6czMLRMYRbhIWF20Kurq4Wd955\nKyZOTIRK1b2bu2Ni4hATE9fh9jPLEHYlhDvi7u7eI+sSn2vTpg2YMSOp0xqIqB+wWCArLDh7y8+Z\n08iZWsiqqto0Nw8JhGHKdOu12jMDo2LjYNEEOMQtPwMNQ7gdnp5e8PPzR2VlJT76aB0UCifU1dXg\n//5vFV599SUUFxfBZDLh7rvvx6WXjsehQ7/hrbdeh6+vH/z8/BEUFIzDhw9h27bP8OKLr553GcI3\n33wPX331X+zYsR2CIMOUKdNx880LUVZWiueeewpOTk6Ijo7tct9LSopx331PY+3aDQCAxYtvw4sv\nrsY///kB/P3VSE8/idLS03j++RcRFxePzZs3YNeuHyEIMtx//0M4deoEMjO1WLbsr7jhhptsNfz4\n4w/YsmUz5HI54uKG4dFHn8D69WvbXXaRiHpBczPk2Vl2ISvXaqHIyoDQ2GjXVJTJYB4aAeOEiS1H\ntrFnp2j09JKoAGpPvwthtxXPQvV1zy5l2HztXDSs6PqiECUlxairq4VGEwDAOifz0qXPYPv2b+Hn\n54+nn34eNTU1+Mtf7seGDZ9i7dp38NxzKxETE4snnngEQUHBtn3p9Q3nXYawvLwMu3b9iH/8Yz0A\n4IEHFmPGjCRs27YFs2bNxvz5N2PTpn8hM1N70X8PBoMBb7zxDr74Yiu2b/8Wrq6u2LXrR6xd+y8U\nFxdh06Z/4amnnsPmzRvw8suv4fDhQy016PHBB+/io48+hqurK5588jHbtnOXXWQIE10coa62ZWCU\n9uzAKG065Hm5ECz2C7mILi4wRcXA3DJFo232qIhIQKWSqAK6EP0uhKWSn5+Hhx66FwCgVCrx7LMv\nQNFyHWT48BEAgNTU4zh27AiOHz8KAGhubobRaERJSQliYqxHq6NHj0Vzc7Ntv50tQ3jyZBoKCwvw\n8MPW6656fQNOny5Gbm4OZsxIAgCMGTMO+/fvbdNnnU5n6zMAREVFn3fxiFGjxgAA1OoAnDiRBq02\nHcOHJ0AmkyEkJBRPPfVcu68rKMhHSEiYbRWoMWMuhVZ7CkDbZReJqAtEEbLS060msUi3zY0sLz3d\nprnFxwemcRPaTtEYEspbfga4fhfCDStevKCj1p7S+prwuRQKJ9vjokV3ITn5SrvtslY/BOdOxd3Z\nMoQKhRMSEyfjySefsfv+5s0bbMsQdvT69q4Jnz5dYvf8fEskyuUyWCydTx0uCPZ1mUxGqFr+l80l\nEonOw2SCPD/Xeq32zEo/Z275qatt09wcEgrDjFktp4/P3vYj+vtL0HnqC/0uhPuz4cMT8OuvPyM5\n+UpUV1fhs88+wX33PQh/fzXy83MRGhqOI0d+x4gRl9he09kyhHFxw/Dee2+jqakJKpUKb775Oh54\n4CGEhYXj1KkTiI8fZjv12xWurm6orKyEKIqoqqpEcXFhh23j4obhX/9aD5PJhLq6Wrz22it45ZU1\nbYI5NDQchYX50Osb4OrqhiNHDuP22xfj0KEDF/6XSOSIGhshz8ywjURGfjZ80k5AnpUJwWCwayo6\nOcEcGQXjlGlnV/qJiYUpKgZwd5eoAJIKQ/gCzJyZhMOHD+L++++C2WzGXXdZTwXfe+8SPPvsUgwZ\nEmi7jnxGZ8sQvv32B5g//2Y8+OA9kMlkmDp1OlQqZ9x448147rmnsHv3TkRFxXS5j56enpg0aRLu\nvnsRoqNjzju6OTAwCFdccTUeeuheiKKI++57EAAQGxuHe+5ZhAceeMRWw4MP/gWPP/4wBEGGkSNH\nY9So0QxhGnSE6ir7KRoz0qHIyICsoO0UjTJ3D5hGJLQaGGU9sjWHDx20UzRSW1zK0AE5eo2sb2Dr\n9/WJImRFha0Wim+57ScjHbKKijbNLWqNbYH4M9dsvSeORbnS02Fv+en3n+FF6ndLGWq1WixZsgR3\n3HEHFi5sf+DP66+/jqNHj2Ljxo3d7yURUV8xGCDPyT47MOrMIKnMDAj6BrumoiDAEj4UzWMubXWt\ntuWWH2+ftvvmZBbURZ2GsF6vx8qVK5GYmNhhm8zMTBw8ePCiJp4gIuoNgq7+7C0/Z0YgZ6RDnpsD\nodXARQAQVSqYo2Ks12pbrV1rjowCXFwkqoAcWachrFQqsW7dOqxbt67DNqtWrcJjjz2Gd955p0c7\nR0TUJaIIobz8nGu11uCVFxe1aW7x8oZp9NhWC8W33PITFg60GvFP1Ns6DWGFQmG7X7Y927Ztw4QJ\nExAcHNxhGyKiHmE2Q1aQ3/4UjTU1bZsHBsEwdYb9KOSYOIgajcNer6WB5aJGR9fU1GDbtm346KOP\nUFpa2qXX+Pi4QqGQ9n+aHV0gdySOXiPrG9g6ra+pCcjIAE6etP+j1Vq3tSaXA9HRwPTpwLBhQHy8\n7VHu4QE5AGVvFXIeg/4zHOD6qr6LCuH9+/ejqqoKt956KwwGA/Lz8/Hyyy9j2bJlHb6mulp/MW95\n0Rx9VB/g+DWyvoGtdX1CbU2bKRoV2nTI8vPaTtHo6gpTbLx1DuTYsyv9mIdGAMp2YrYJQJM0f4+D\n6TN0RP1udHRHrrzySlx5pXX2qMLCQjz99NPnDWAiGoREEbKSYttC8SjIgdcfadZrt2Vtz6BZ/P1t\nCw+cuVZrjo2DJSiYUzSSw+k0hFNTU7F69WoUFRVBoVAgJSUFM2fOREhICJKTk/uij0Q0EJhMkOfm\nnLN2bcsUjTr7owolAHNYOAwzk1qtXWsNXdHXT5r+E0mg0xBOSEjo0r2/ISEhvEeYaDBoaIAiK8Nu\nxih5Rjrk2VkQjEa7pqKTE8xR0TC2Wk7P87KxKPcNAloWBCEazDhtJRG1S6istL/lR5sOeWYG5AX5\nbdpa3D1gumRkyxSNLddqY2JgDo8Azr27ghNZENkwhIkGM4sFssKCVqePz55GllVVtWluDhgCw5Rp\nMEfHtLrHNg6WIYG85YeoGxjCRIOBwQB5dtbZSSzOBG5WBgS9/R0LokwG89AIGMdfdnah+OgY6xSN\nXt4SFUDkmBjCRA5EqK9rtVB8y9q12nTI83IhmM12bUVnZ5iiY62njc+E7ZkpGlvWiyai3sUQJhpo\nRBGyslJruGqtq/vIzwyOOl3SprnFxwemS8e3naIxNIy3/BBJjCFM1F+ZzZDl5dpOH1vDtuWWn7ra\nts2DQ2CYPtPuWq0pJg6ivz+v1xL1UwxhIqk1NkKemdGydm06kJ8Nn9Q0yLMyIRgMdk1FhQLmyCgY\nL59qW8PWHBsHU1QM4O4uUQFE1F0MYaI+IlRXQa5ttXZtphYKrRaygjwIomjXVubmDtPwEa0GRsWe\nnaKRS4YSOQyGMFFPEkXIiovOnj4+s9JPhhayivI2zS1qDYyJk+2maPROvBSVSk+eQiYaBBjCRN1h\nNNqmaGx9ZCvPyICsQWfXVBQEWMLC0TxmrN1yeuaYGIg+vm33zcksiAYNhjDR+eh01mu156z0I8/J\nhmAy2TUVVSqYI6NhaH2tNjoW5qhowMVFogKIqD9jCBOJIoSKivanaCwqbNPc4ukF06gxZ++rjYmF\nKSYWlvCh1rVtiYi6iCFMg4fFAllBvv212jNTNNbUtGluDgyCYcp0u+X0zDGxsGgCeL2WiHoEQ5gc\nT3Mz5FmZdsvpKbRayLMyIDQ12TUV5XLrFI0TJ7ecPo6xha3o4SlRAUQ0WDCEacAS6mo7nqLRYrFr\nK7q6whQbb71WG9PqyDYiElAqJaqAiAY7hjD1b6II2emSloFR1tPHyM2C74mTkJeebtPc4ucH44SJ\nLddqY2zXbS3BIZyikYj6HYYw9Q8mE+R5OXb31dqmaKyva9s+NAyGmUktt/q0mqLRz6/v+05E1E0M\nYepbej0UWRmtRiG3hG12FgSj0a6p6ORknaIxZgZMsbG2kcg+E8eiSm/p4A2IiAYOhjD1CqGysmXB\ngdaLD2ghL8hv09bi7gFTwiX2y+nFxsIcNrT9KRrd3AA9J7MgooGPIUzdZ7FAVlTY6lafjJZTyemQ\nVVa2aW7WBMAweYp1YJQtbONgGRLIW36IaFBiCFPnDAbIc7Ltj2gztFBkaiHo9XZNRZkM5vChMF46\nvtXiAzHWW368fSQqgIiof2IIk41QX3c2YFtOI8sz0iHPzYFgNtu1FZ2dYY6KsV6rbbV2rTkyCnB2\nlqgCIqKBhSE82IgihLIy2xSNioyzp5HlJcVtmlu8vWEaO67VcnrWe2wtoWGcopGI6CIxhB2V2QxZ\nXm7LQvFau/mQZbXtTNEYFAzDtBl212pN0bEQ1WperyUi6iUM4YGusRHyrMyWsLVer0V2Bvy1WgjN\nzXZNRYUC5ohIGCdd3nL6uGWh+OgYiO4eEhVARDR4MYQHCKGmGnKtttXAKOuRrSw/D4Io2jd2c4Mp\nfnjbKRqHRnCKRiKifoQh3J+IImQlxa0WitfaFiGQlZe1aW7xV8M4cdLZKRpbwtZvVDxqKhskKICI\niC4EQ1gKRiPkuTl2R7TyTK11ikad/SQUoiDAEhqO5qTZrdautYau6NvBFI2cI5mIaEBgCPcmna7V\nFI3as2Gbk912ikalEuaoaBjOmQvZHBUNuLhIVAAREfUmhvDFEkUIFRVtrtXKM7SQFxW2aW7x8IRp\n5CjrRBZnRiHHxMISFg4o+HEQEQ0m/K3fVRYLZAX5ba7VyjPSIauubtPcPCQQhinT7a7VmmPjYNEE\n8JYfIiICwBBuq7kZ8uws+2u1Wi0UWRkQGhvtmooyGcxDI2zr11rvsbWOSBY9vSQqgIiIBopBG8JC\nXe3ZKRptYZsOeV5u2ykaXVxgio49e8vPmQktIiIBlUqiCoiIaKBz7BAWRcjKSq3h2nLbD3Kz4Hvi\nJOSnS9o0t/j6wjRugu2I9kzYWoJDOOKYiIh6XJdCWKvVYsmSJbjjjjuwcOFCu22fffYZtm7dCplM\nhvj4eCxfvhxCX1/zNJkgz8+1XqvVpltnj2qZE1lWV9u2fUgoDDNm2U/RGBMH0a+DW36IiIh6Qach\nrNfrsXLlSiQmJrbZ1tjYiG+//RabN2+Gk5MTFi1ahCNHjmDs2LG90tlzybKz4HnvnVCcOgHBYLDb\nJjo5wRwZBeOUadaVflrC1mfiWFTpLX3SPyIiovPpNISVSiXWrVuHdevWtdnm4uKCDRs2ALAGsk6n\ng1qt7vledkBoaICsphqmEQkwR9svFG8OHwo4ObV9kZsboK9v+30iIqI+1mkIKxQKKDq5f/WDDz7A\nv//9byxatAihoaE91rnOmC8ZiapDf/TZ+xEREfUkQRTPnf2/fW+//TZ8fHzaXBM+o6mpCffccw8e\nffRRXHrppR3ux2QyQ6HgOrREREQXNTq6pqYGGRkZGD9+PJydnTF16lQcPnz4vCFcXa2/mLe8aGq1\nB8rLHft0tKPXyPoGNkevD3D8Gllf9/bZnou678ZkMuGpp55CQ4N1xZ4//vgDERERF7NLIiKiQaPT\nI+HU1FSsXr0aRUVFUCgUSElJwcyZMxESEoLk5GQ8+OCDWLRoERQKBeLi4jBr1qy+6DcREdGA12kI\nJyQkYOPGjR1unzdvHubNm9ejnSIiIhoMOA0UERGRRBjCREREEmEIExERSYQhTEREJBGGMBERkUQY\nwkRERBJhCBMREUmEIUxERCQRhjAREZFEGMJEREQSYQgTERFJhCFMREQkEYYwERGRRBjCREREEmEI\nExERSYQhTEREJBGGMBERkUQYwkRERBJhCBMREUmEIUxERCQRhjAREZFEGMJEREQSYQgTERFJhCFM\nREQkEYYwERGRRBjCREREEmEIExERSYQhTEREJBGGMBERkUQYwkRERBJhCBMREUmEIUxERCQRhjAR\nEZFEGMJEREQS6VIIa7VaJCUlYdOmTW227d+/H/Pnz8eCBQvw9NNPw2Kx9HgniYiIHFGnIazX67Fy\n5UokJia2u/3555/HW2+9hU8//RQNDQ345ZdferyTREREjqjTEFYqlVi3bh00Gk2727dt24YhQ4YA\nAHx9fVFdXd2zPSQiInJQnYawQqGAs7Nzh9vd3d0BAGVlZdizZw+mTZvWc70jIiJyYIqe2EllZSXu\nv/9+LF++HD4+Pudt6+PjCoVC3hNv221qtYek798XHL1G1jewOXp9gOPXyPp6xkWHsE6nwz333INH\nH30Ul19+eaftq6v1F/uWF0Wt9kB5eb2kfehtjl4j6xvYHL0+wPFrZH3d22d7LvoWpVWrVuH222/H\n1KlTL3ZXREREg0qnR8KpqalYvXo1ioqKoFAokJKSgpkzZyIkJASXX345vvjiC+Tl5WHr1q0AgGuu\nuQY33XRTr3eciIhooOs0hBMSErBx48YOt6empvZoh4iIiAYLzphFREQkEYYwERGRRBjCREREEmEI\nExERSYQhTEREJBGGMBERkUQYwkRERBJhCBMREUmEIUxERCQRhjAREZFEGMJEREQSYQgTERFJhCFM\nREQkEYYwERGRRBjCREREEmEIExERSYQhTEREJBGGMBERkUQYwkRERBJhCBMREUmEIUxERCQRhjAR\nEZFEGMJEREQSYQgTERFJhCFMREQkEYYwERGRRBjCREREEmEIExERSYQhTEREJBGGMBERkUQYwkRE\nRBJhCBMREUmEIUxERCQRhjAREZFEuhTCWq0WSUlJ2LRpU5ttzc3NWLp0KebNm9fjnSMiInJknYaw\nXq/HypUrkZiY2O72V199FcOGDevxjhERETm6TkNYqVRi3bp10Gg07W5/7LHHkJSU1OMdIyIicnSK\nThsoFFAoOm7m7u6OmpqaLr+hj48rFAp5l9v3BrXaQ9L37wuOXiPrG9gcvT7A8WtkfT2j0xDuadXV\n+r5+SztqtQfKy+sl7UNvc/QaWd/A5uj1AY5fI+vr3j7bw9HRREREEmEIExERSaTT09GpqalYvXo1\nioqKoFAokJKSgpkzZyIkJATJycl45JFHcPr0aeTk5OC2227D/Pnzce211/ZF34mIiAa0TkM4ISEB\nGzdu7HD7W2+91aMdIiIiGix4OpqIiEgiDGEiIiKJMISJiIgkwhAmIiKSCEOYiIhIIgxhIiIiiTCE\niYiIJMIQJiIikghDmIiISCIMYSIiIokwhImIiCTCECYiIpIIQ5iIiEgiDGEiIiKJMISJiIgkwhAm\nIiKSCEOYiIhIIgxhIiIiiTCEiYiIJMIQJiIikghDmIiISCIMYSIiIokwhImIiCTCECYiIpIIQ5iI\niEgiDGEiIiKJMISJiIgkwhAmIiKSCEOYiIhIIgxhIiIiiTCEiYiIJMIQJiIikghDmIiISCJdCmGt\nVoukpCRs2rSpzba9e/fihhtuwE033YR33323xztIRETkqDoNYb1ej5UrVyIxMbHd7S+++CLefvtt\nfPLJJ9izZw8yMzN7vJNERESOqNMQViqVWLduHTQaTZttBQUF8PLyQmBgIGQyGaZNm4Z9+/b1SkeJ\niIgcjaLTBgoFFIr2m5WXl8PX19f23NfXFwUFBT3XOyIiol5mtphxojIV+4r3YH/JPhiERqyduQFu\nTm69/t6dhnBP8/FxhUIh7+u3taNWe0j6/n3B0WtkfQObo9cHOH6NA7k+g9mAQ8WHsDtvN3bn7cae\ngj2oa66zbR+uHg5/f3e4K917vS8XFcIajQYVFRW256Wlpe2etm6tulp/MW950dRqD5SX10vah97m\n6DWyvoHN0esDHL/G/lxfo6kRpxtKUKYvQ5n+NMr0pSjTl6K0oeVRX4qM6nQ0mZtsr4n0isK1kXMx\nMXASEoMmY2zkCFRU6NCInquxo/+0XFQIh4SEQKfTobCwEEOGDMHOnTuxZs2ai9klERHRBcmqycAP\neSn4Ie977C/eA6PF2GFbF4ULIr2jkRg0CYmBk3FZ0CQEuAbYtREEobe7bNNpCKempmL16tUoKiqC\nQqFASkoKZs6ciZCQECQnJ2PFihV4/PHHAQBXX301IiIier3TREQ0eDWbm7G36FfsyEvBjvzvkVOb\nbds2Uj0aw/1GQOMSAI2rBgFuQ6BxtX6tcQ2Au5NHn4ZsZzoN4YSEBGzcuLHD7ePHj8eWLVt6tFNE\nREQAYBEtyKvLxamqkzhZmYajZYexu/Bn6E0NAAB3Jw/MibwOyeFXYFZYMgLchkjc4wvT5wOziIiI\nWhNFEQ1GHcoay1BQl4+TVWk4VXkSJ6vSkF51CnqT/ViiaO8YzAqfjeTwKzAxcBKUcqVEPb94DGEi\nIupxFtGCmuZqVOgrUNFYjorGcpQ3lqFcX4byxvKWxzKU663fbzQ1ttmHk8wJMT5xiPcdhuF+IzDM\ndziG+Y1AiEeoBBX1DoYwERF1W7O5GUfKDmNf0a84ePoAShpKUNFYjsqmCpgspvO+1knmBH8XNWJ8\n4qB2UUPtqkGQWxDifYcj3m84oryi4SR36qNKpMEQJiKiLmsyNWF33hF8m5aCfcV7cPD0Abvbfdyd\nPODv4o/R6rFQu2rg76KG2sUf/i5q69euGqhdNFC7quGt8ulXg6SkwBAmIqLzyqvLxTdZX2FHXgoO\nlf6GZnOzbdsw3xGYHHw5EoP9QGCNAAAbxElEQVQuR2LQZPi7+EvY04GHIUxERG1k12bhm6wv8XXW\nlzhWfgQAIEDACP9LMCtqBsb4XIaJQYnwdfaTuKcDG0OYiIgAABnVWnyd9QW+zvoSaZV/AAAUMgVm\nhM7CtVFzcWXEHPi7+PfrGbMGGoYwEdEgVNFYgePlR1v+HMPx8qPIr88DYB0wlRx+Ba6Nmosrhl4F\nH2ffTvZG3cUQJiJycA3GBhwo2YcjZb/bArdIV2jXxs/ZD1dFXINrIq/DFUOvgqfKS6LeDi4MYSKi\nfq62uQYF9QUI9QiFl8q70/YmiwlHyn7H7sJd2F24C4dO/2Y3n7LaRYOksNkYqRmNkf6jMUo9GkHu\nwYN+pLIUGMJERP1Qk6kJP+Sl4HPtZ9iRlwKDxQAA8FZ5I9wzAuGeQ+3+eKu8cfD0Aewu3IU9xb+i\n3mBdmk+AgFHq0ZgSMh0TAidilHo0hrgFSlkatcIQJiLqJ8wWM/YU/4LPtZ/hm+yvbEEa7zsME4Yk\n4nRDMfLqcpFeddI2Yrk9kV5RmBdzI6aGTMflwVN4TbcfYwgTEV2kJlMTnBXO3XptvaEOqRV/4Luc\nb/BFxuco1Z8GAAS5BeP2EXfhzzHzMdxvhN2pYotoQZm+FLl1ucirzUFeXS4qGssxWjMWU0KmIdQj\nrEfqot7HECYi6qbfSw/ipf0v4Nei3fB38Ue0dyxifGIxOuQSBDqFIdo7FqEeYZDL5LCIFuTWZiOt\nMg1plX/gRGUaTlSk2kYkA9ZTzbcNvxN/jrkRE4MmQSbI2n1fmSDDELdADHELxMTAxL4ql3oBQ5iI\n6AKdqjqJlw/8H7bnfAsAGKUeg9rmGvx2ej/2l+zFxhNn26rkKoR4hKJEV9xmNSB/F39MDZmB4X4j\nkBg0GTPDkqCSq/qyFJIYQ5iIqIvy6/Lw6sGX8Z/0TyFCxIQhE/HsxBWYGDQJgPW0dE5tNsosBfg9\n7xgyazKQWa1Fbl0Owj0jMNxvBEb4X2J71LhoOCJ5kGMIExF1okxfhr/9/ir+nfYRjBYjhvsl4JnL\nnkdS+BV2IeqscMYwv+GYqr4M09RXSNhjGigYwkRE7bCIFhw6fRBfZG7Fxyc3QW9qwFDPCCyd8Az+\nFHNDh9driS4EQ5iIHJpFtHQ5MM8E79dZ/8VXWV+gpKEYABDgOgQrJr2IW4ctcvj1balvMYSJyOHU\nNdfiu5xv8Ln2M/xatBs+zr4tk1qEtzyenexiiFsgDpf+jq+z/ouvs75EcUMRAMBL5Y2b4xfiuqi5\nmBIyHUq5UuKqyBExhInIITSbm7Ej73tsy/gPvs/9n23N2+F+CWg06XGs/Ah+Lz3Y5nUCBIgQAViD\nd0H8rbg+6k8MXuoTDGEiGrAsogV7i3/F59rP8HXWl6gz1AIAYrxj8efY+ZgXcyOGekUAsM5GVdIy\n45T1j3WSi4L6AkR6ReH66D9hasgMBi/1KYYwEQ045fpyfHJqI/6d9pFtsotAtyAsHH47/hxzIxL8\nR7a59UcukyPEIxQhHqGYHDxFim4TtcEQJqIBQRRF7Cvegw1p6/FN9lcwWoxwVbjilvjbcGPcAkwM\nnAS5TC51N4kuCEOYiPqERbSgWFeE4/UlOJz3B7Jrs1BQnw9Ppaf1CNXdepQa7BGCYPcQ28xRtc01\n+Cz9E2xI+ye01ekAgDifeNyRsBg3xi7gurc0oDGEiajHGc1G7Cn+BT8X7ERWbSZya7ORW5uDJnNT\nl/ehcQ1AkFsQ0qtPodHUCKVMiXkxN+KOEYtxWWAiZ5oih8AQJqIeYTAb8EvhLnyd9SX+l/MNqpur\nbds8lJ6I8x2GSK9IJAQNR4BTCCK8IhHuGYF6Qy0K6wtRWF+AQl0BCusLUKQrREF9PtIqUxHkHoxF\nI+7CzfEL4e/iL2GFRD2PIUxE3dZsbsbPBT/h66wvsT33O9Q21wCwTm6x+JJ7ceXQORjulwB/F3/b\nkata7YHy8nrbPjSuGkR5x7S7/wuZaINoIGIIE9EFO1l5AuuOv4cvs/5rW3g+yC0YC+JuwTVRczF+\nyIQeCU8GMDk6hjARdYlFtGBHXgrWHn8PvxTuAgCEuIdi4bDbcV30XIzRXMrQJLpADGEiOi+doR5b\n0j/GB8ffQ05tNgBgSvA03DtqCZLCZvO2IKKLwBAmIoiiiGZzM5pMjdZHcxPqmmvxH+0WbD75b9Qb\n6qCSq3DrsEW4+5L7McI/QeouEzkEhjDRIGCymJBVk4m0yj+QWvEHUiuOQ1uVjgZTA5pNTee9dUjj\nGoAHRz+CRSPu4uhkoh7GECZyMKIoIqNai1+KfkZaxR9Iq/wDJytPtAnaYHfrpBjOchVUCmc4y52h\nUjjDpeVRJXfGhCGX4froeZxPmaiXdCmEX375ZRw7dgyCIGDZsmUYOXKkbduOHTvw3nvvQalUYs6c\nOVi4cGGvdZaI2meymHDw9AFsz/kO23O/tV27BQClTIk432FI8L+k5c9IDPcbAS+Vt4Q9JiKgCyH8\n22+/IS8vD1u2bEFWVhaWLVuGLVu2AAAsFgtWrlyJ//73v/D29sY999yDpKQkDBkypNc7TjTY6Yw6\n7Mr/CSm53+GHvO2oaqoCALg5uePaqLlICpuNUZoxiPGO5UL0RP1UpyG8b98+JCUlAQCioqJQW1sL\nnU4Hd3d3VFdXw9PTE76+vgCAiRMnYu/evZg3b17v9ppoEBBFEXUts0kV6QpQqCtEcX2RbVapY+VH\nbGvmDnELxO0jFuOqiKsxOXiqbd5lIurfOg3hiooKjBgxwvbc19cX5eXlcHd3h6+vLxoaGpCbm4vg\n4GAcOHAAEyZM6NUOEzkik8WEU1Uncbj0EE7UHsP+gt+QV5eLBqOu3fYyQYY4n2G4KuJqXBkxByPV\no3mPLtEAdMEDs0RRtH0tCAJWrVqFZcuWwcPDAyEhIZ2+3sfHFQqFtPcVqtUekr5/X3D0Ggd6fUV1\nRThQdAD7C/fjQNEBHCo+BL1Rb9vu6uSKaN9ohHmFIcwzDKFeodavvcIQ6hmKII+gAX2KeaB/fl3h\n6DWyvp7RaQhrNBpUVFTYnpeVlUGtVtueT5gwAR9//DEA4PXXX0dwcPB591ddrT/v9t527ry1jsjR\naxyI9TWZmrC3+FfszN+BH/N/QGZNhm2bAAHxvsMwNmAcxgaMQ1L8NKgRCoWsgx9PI1BT1QSg6ysS\n9ScD8fO7UI5eI+vr3j7b02kIT548GW+//TYWLFiAtLQ0aDQauLu727bffffdWL16NVxcXLBz507c\neeedPddrogFKFEXk1Gbhx/wf8FP+Duwt/hWNpkYAgKvCDcnhV2DCkIkYGzAOozVj4KH0tL3W0X/B\nEdFZnYbw2LFjMWLECCxYsACCIGD58uXYtm0bPDw8kJycjPnz5+Ouu+6CIAi49957bYO0iByd0WxE\nqf40inXFON1QjOKGIhTrilGiK8bR8sPIq8u1tY33HYaZYcmYGZaEywITOXCKiAB08ZrwE088Yfc8\nPj7e9vXs2bMxe/bsnu0VUS/RGepxquokVHIVXJ1c4aJwhYvCBS4KV6jkKttyewazAacbSlCsK7KF\na7Gu0BqyLc/L9KUQIbb7Ph5KT8yJvA6zwpIxI3QWgj06Hy9BRIMPZ8wih2cRLdhT9As+PbUZ32Z/\nBb2p/XEJMkEGF4UrlDInuwXpz6WSqxDoFoSJQZMQ6BaEIPdgBLoFItAtGEHuQQh0C4LGNYALGxBR\npxjC5LCya7Pw2amP8Vn6pyjUFQAAwjyH4sqhVwEA9EY99CY9Gk2NaLQ9NqLZ1IThfgkIdA9CsHuI\n7THILQiB7sHwc/azHTETEV0MhjA5lNrmGnyd9SW2pH+MAyX7AFhnkLol/jbcFH8LLgtM5P20RNRv\nMIRpQDNZTDhS9jt2FfyEXQU/4XDpIZhFMwQImBIyHQvibsHVkdfCzclN6q4SEbXBEKYBJ7s6G5+n\nfoWfC3fil8KfUWeoBWC9pjtGcylmh1+JG+MWIMQjVOKeEhGdH0OY+r2qpkr8Wrgbuwt/xu7Cncit\ny7FtC/MIx9zoP2N66ExcHjwF3s4+EvaUiOjCMISp39Eb9ThQsg+7C3fhl6Kf8Uf5MdutQB5KT8yN\nn4tEzVRMC52BCM9IDpIiogGLIUySaTY3o6AuHzm1WcipzUZOXTZOVp7AodO/wWAxALCuhTsp6HJM\nDZmOqaHTMUo9BoEBPpxRiogcAkOYep3JYsLJyjQcKj2IE5VpyKnNRm5tNgp1BbCIFru2AgRcoh6F\nqSHTMSV4Gi4LTISrk6tEPSci6l0MYeoSURSRWvkHIIrwUnnDS+UFD6Vnu7f7lOpL8fvpg/i99CAO\nlf6GY2VH2kyQMcQtEJcFJiLCMxIRXpEY6hWBCC/r163nUSYicmQMYerUvuI9WLlvOQ6V/mb3fQEC\nPFVe8FJ6wUvlDU+lJ/Lr81BQn2/XJt53OMYNGY9xARNwiXoUIrwiecsQEREYwnQeaRWpeGn/CuzI\n/x4AcOXQqxHqEYaa5hrUGWqtj83Wx6yaTOhNDfB19kVy+BUYFzABlw4ZjzGasTyyJSLqAEOY2sir\ny8Xq317C59rPIELE5KApeDZxBS4NGH/e1xnNRihkCo5WJiLqIoYw2ZTry/G331/FhrR/wmgxYoTf\nJXgucQVmhCZ1KVid5E590EsiIsfBEHZwoigiteI4tud+h7y6XBjNBhgsxpZHA4xmY8ujARk1GWgw\n6hDmORRPT3gWf4q5gfMsExH1IoawAzKYDfi5YCe2536LlJz/2VYQ6ohCpoBSpoSfiz+enbgctw2/\nE0q5so96S0Q0eDGEB4hGUyPMFhNEiBBF6+xRrb82WIzYU7Qb23O+xU8FO1DbbJ1P2UvljXkxN+Kq\niDkYrRkLZ7kznOROUMqUcJIr4SRz4tEuEZFEGML9lEW04EjZ7/ghLwU/5Kbgj4pjXX5tuFc45sfe\njCsj5mBi4CReqyUi6qcYwv1IvaEOuwp+wve52/Fj/g+oaCwHADjJnJAYNBkeTh4AAEEQIKBloFTL\ngCkZZEjwvwRXRszB9PhEVFToJKmBiIi6jiHcB0p0xcipzUaDUYcGY0PLn1Zfm3TQVqVjX8kemCwm\nAIDaRYNb4m9DUvgVmB46A+5Kjy6/H28RIiIaGBjCvahYV4TXD72Kj0/+G2bR3Gn7UeoxSA6/Asnh\nV2CUZgyv1RIROTiGcC8o15fjrcOv419p69Fsbka0dwyujboe7kpPuDm5wU3hBjcnd+vXLY8a1wCo\nXdVSd52IiPoQQ7gH1TRV4x9H38YHx9+D3tSAUI8w/HX807gh9iYoZPyrJiIie0yGHqAz6vDh8ffx\n7tG3UNtcA41rAJ5LfAELh98OlVwldfeIiKifYgh3Q3VTFY6UHcbRlj8HSvahurkaPiofPJ+4Encl\n3MM1cImIqFODOoR1hnr8kJeC/Lo8uChc4KxwgbPCGS4KV7i0PDornNFsasax8qM4WvY7jpQdRm5d\njt1+gtyCcdcl9+KBUQ/BU+UlUTVERDTQDLoQ1hv1+DrrC/w343PsyEtBk7npgl7vrfLG9NCZGKu5\nFKM1l2KMZiwC3Ib0Um+JiMiRDYoQbjY3Y2f+j/gicytScv+HBmMDACDaOwbXR8/DpQHj0Gw2oMnU\niEZTI5pMjdC3PDaZmyBAQIL/JRitGYuhnhG8D5eIiHrEgA7hE5VpuON/t8BoMUIpV8JZ7gyVXAWl\nXAWVwhnOchUECNhfsg91ButcypE+kbg24k+4PnoeRvglMFCJiEgyAzqEVXIlvFTeqG6qgt6oR3VT\nFQxmAxpNjRAh2toFu4fg1mGL8KeYPyNp+FRO6UhERP3CgA7hKO8Y/HDjz22+L4oiTBYTmi3NMJib\n4a3ysc0+xSNfIiLqLwZ0CHdEEAQ4yZ2sqwc5uUvdHSIionZxcmIiIiKJMISJiIgk0qXT0S+//DKO\nHTsGQRCwbNkyjBw50rZt8+bN+OqrryCTyZCQkIBnnnmm1zpLRETkSDo9Ev7tt9+Ql5eHLVu24KWX\nXsJLL71k26bT6bB+/Xps3rwZn3zyCbKysnD06NFe7TAREZGj6DSE9+3bh6SkJABAVFQUamtrodNZ\nb/FxcnKCk5MT9Ho9TCYTGhsb4eXFaRuJiIi6otPT0RUVFRgxYoTtua+vL8rLy+Hu7g6VSoUHH3wQ\nSUlJUKlUmDNnDiIiIs67Px8fVygU8ovv+UVQqz0kff++4Og1sr6BzdHrAxy/RtbXMy74FiVRPDsJ\nhk6nw9q1a7F9+3a4u7vj9ttvx6lTpxAfH9/h66ur9d3raQ9Rqz1QXl4vaR96m6PXyPoGNkevD3D8\nGllf9/bZnk5PR2s0GlRUVNiel5WVQa1WAwCysrIQGhoKX19fKJVKjBs3DqmpqT3UZSIiIsfWaQhP\nnjwZKSkpAIC0tDRoNBq4u1snwAgODkZWVhaamqwrEaWmpmLo0KG911siIiIH0unp6LFjx2LEiBFY\nsGABBEHA8uXLsW3bNnh4eCA5ORmLFy/GokWLIJfLMWbMGIwbN64v+k1ERDTgCWLri7x9QOrrCI5+\nLQNw/BpZ38Dm6PUBjl8j6+vePtvT5yFMREREVpy2koiISCIMYSIiIokwhImIiCTCECYiIpIIQ5iI\niEgiDGEiIiKJXPDc0f3Rha53bDKZ8MwzzyA/Px9msxlPPvkkxo0bh9tuuw16vR6urq4AgKVLlyIh\nIUGqsmwutL5t27bhzTffRFhYGABg0qRJeOCBB3Dq1CmsWLECABAXF4cXXnhBinLadaE1vvfee9i7\ndy8AwGKxoKKiAikpKZg5cyaGDBkCudy6SMiaNWsQEBAgSU2tna++HTt24L333oNSqcScOXOwcOHC\nDl9TUlKCJ598EmazGWq1Gq+99hqUSqVUZdl0p75XX30Vv//+O0wmE+677z7Mnj0bTz31FNLS0uDt\n7Q0AWLx4MaZPny5FSXYutL4DBw7gL3/5C2JiYgAAsbGxeO655/rt5wdceI3/+c9/8NVXX9napKam\n4siRI/3296hWq8WSJUtwxx132P4NnrF371688cYbkMvlmDp1Kh588EEAffQzKA5wBw4cEO+9915R\nFEUxMzNTnD9/vm1bfX29OGPGDNFoNIqiKIp33nmneOTIEXHr1q3i8uXLRVEURa1WK/75z38WRVEU\nFy5cKKanp/dtAZ3oTn2ff/65uGrVqjb7WrhwoXjs2DFRFEXx//2//yfu2rWrDyroXHdqbG3btm3i\nunXrRFEUxRkzZog6na6Pet4156vPbDaLU6dOFSsrK0Wz2SzeddddYklJSYeveeqpp8TvvvtOFEVR\nfP3118XNmzf3cTVtdae+ffv2iXfffbcoiqJYVVUlTps2TRRFUVy6dKn4008/9XkN59Od+vbv3y8+\n/PDDbfbVHz8/Uexejee+fsWKFaIo9s/fow0NDeLChQvFZ599Vty4cWOb7VdddZVYXFwsms1m8eab\nbxYzMjL67GdwwJ+O7s56x9dddx2efvppANalGWtqaiTrf2d6aj1ng8GAoqIi2/9uZ8yYgX379vVN\nEZ24mBpNJhM++eSTNv+z7U/OV191dTU8PT3h6+sLmUyGiRMnYu/evR2+5sCBA5g1axaA/vMZdqe+\n8ePH48033wQAeHp6orGxEWazWbIazqc79XWkP35+wMXX+O6772LJkiV93u+uUiqVWLduHTQaTZtt\nBQUF8PLyQmBgIGQyGaZNm4Z9+/b12c/ggA/hiooK+Pj42J6fWe8YgN16xzNmzMCoUaMQEREBJycn\nqFQqAMCGDRtwzTXX2F7/1ltv4dZbb8Xzzz9vW5hCSt2pDwB+++03LF68GLfffjtOnDhh+0E6w8/P\nz7YfqXW3RgD4/vvvcfnll8PZ2dn2veXLl+Pmm2/GmjVr7JbelMr56vP19UVDQwNyc3NhNBpx4MAB\nVFRUdPiaxsZG26mv/vIZdqc+uVxuO125detWTJ061XYJYdOmTVi0aBEee+wxVFVV9X1B5+hOfQCQ\nmZmJ+++/HzfffDP27NkDAP3y8wO6XyMAHD9+HIGBgbbV9YD+93tUoVDY/Y5orby8HL6+vrbnZ2rv\nq59Bh7gm3Jp4Aesdb968GWlpaXj//fcBAIsWLUJcXBzCwsKwfPlybN68GYsXL5akjo50pb5Ro0bB\n19cX06dPx5EjR7B06VJ8+OGHHe6nv7mQz/Dzzz+3u7b9yCOPYMqUKfDy8sKDDz6IlJQUXHnllX1e\nw/m0rk8QBKxatQrLli2Dh4cHQkJCOn3N+b7XH1xIfTt27MDWrVvxz3/+EwBw/fXXw9vbG8OGDcMH\nH3yAd955B88//3yf9r8zXalv6NCheOihh3DVVVehoKAAixYtwvfff9/hfvqbC/kMt27dij/96U+2\n5wPh92h39NbP4IA/Eu7uesf/+c9/8NNPP+Ef//gHnJycAADJycm2wUwzZ86EVqvt42ra6k59UVFR\ntsEsY8aMQVVVFXx8fOxOu5eWlrZ7akYK3f0M9Xo9Tp8+bfdLYe7cufDz84NCocDUqVP7/WcIABMm\nTMDHH3+MtWvXwsPDA8HBwR2+xtXV1XZk0V8+w+7UBwC//PIL3n//faxbtw4eHtbJ7RMTEzFs2DAA\nA+NnEGi/voCAAFx99dUQBAFhYWHw9/dHaWlpv/z8gO5/hoD1FPuYMWNsz/vj79HzObf2M59LX/0M\nDvgQ7s56xwUFBfj000/xzjvv2E5Li6KIO+64A3V1dQCs/7DOjGyUUnfqW7duHb755hsA1hGBZwIs\nMjIShw4dAmA9jTtlyhQJKmqru2tWnzp1CpGRkbb91NfXY/HixTAYDACAgwcP9vvPEADuvvtuVFZW\nQq/XY+fOnUhMTOzwNZMmTbJ9v798ht2pr76+Hq+++irWrl1rGwkNAA8//DAKCgoADIyfQaD9+r76\n6iusX78egPV0Z2VlJQICAvrl5wd0r0bAGkJubm6207P99ffo+YSEhECn06GwsBAmkwk7d+7E5MmT\n++xn0CFWUVqzZg0OHTpkW+/4xIkTtvWOP/30U2zbts223vGTTz6JN954A99++y2CgoJs+1i/fj12\n7NiBDz/8EC4uLggICMBLL70EFxcXCSuzutD6Tp8+jb/+9a8QRREmk8k2tD4zMxPPP/88LBYLRo0a\nZRuc1h9caI0AkJKSgr1799qdjt6wYQO++OILqFQqDB8+HM899xwEQZCqLJvz1ff999/j3XffhSAI\nuOuuu3Dddde1+5r4+HiUlZVh6dKlaG5uRlBQEF555RXbmRwpXWh9W7Zswdtvv213fX/16tXIz8/H\na6+9BhcXF7i6uuKVV16Bn5+fhJVZXWh9Op0OTzzxBOrq6mA0GvHQQw9h2rRp/fbzA7r3bzQ1NRV/\n//vf7S53fffdd/3u92hqaipWr16NoqIiKBQKBAQEYObMmQgJCUFycjIOHjyINWvWAABmz55tO33e\nFz+DDhHCREREA9GAPx1NREQ0UDGEiYiIJMIQJiIikghDmIiISCIMYSIiIokwhImIiCTCECYiIpII\nQ5iIiEgi/x9HEf6b2I46JwAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jgmH3wwt1src",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Okay, so we are doing good!
\n",
+ "\n",
+ "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
+ "\n",
+ "Or better, do it yourself!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OZ5TY7B_4E_v",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n",
+ " X = np.linspace(-30.0, 300.0, 300)\n",
+ " Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ " \n",
+ " X = X / np.max(X)\n",
+ " Y = Y / np.max(Y)\n",
+ " \n",
+ " train_X = X[:250]\n",
+ " train_Y = Y[:250]\n",
+ "\n",
+ " test_X = X[250:]\n",
+ " test_Y = Y[250:]\n",
+ " \n",
+ " x = tf.placeholder(tf.float32, name='x')\n",
+ " y = tf.placeholder(tf.float32, name='y')\n",
+ " \n",
+ " W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ " b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ "\n",
+ " pred_y = (W*x) + b\n",
+ " \n",
+ " loss = tf.reduce_mean(tf.square(y - pred_y))\n",
+ " \n",
+ " optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)\n",
+ " \n",
+ " with tf.Session() as sess:\n",
+ " \n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "A6MaclhK4rc6",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 549
+ },
+ "outputId": "a66fb19e-3548-46b8-897a-7694b9dfc500"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Okay! Now let's tweak!\n",
+ "linear_regression(learning_rate=0.000034, n_epochs=500)"
+ ],
+ "execution_count": 46,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.2740557\n",
+ "Loss after epoch 50 is 0.272346\n",
+ "Loss after epoch 100 is 0.27064922\n",
+ "Loss after epoch 150 is 0.26896554\n",
+ "Loss after epoch 200 is 0.26729465\n",
+ "Loss after epoch 250 is 0.2656364\n",
+ "Loss after epoch 300 is 0.2639907\n",
+ "Loss after epoch 350 is 0.26235753\n",
+ "Loss after epoch 400 is 0.2607367\n",
+ "Loss after epoch 450 is 0.25912824\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.006099384\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAe0AAAFKCAYAAAAwrQetAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3XlYlGX3wPHvMzMsIiCLgwu4IqKy\nuGYuuaC4V1qpqZmVW4talqWFlfZqZqX+yjJT05Y3Tcq0bBO1zOrVsFxQcEfBDdlEYNhn5vn9AQ5S\nKi7gMMP5XBeXDHPPwzlMcbjv514UVVVVhBBCCFHlaawdgBBCCCGujxRtIYQQwkZI0RZCCCFshBRt\nIYQQwkZI0RZCCCFshBRtIYQQwkborB3AtaSmZls7BDw9XcjIyLV2GJVG8rNt9p4f2H+Okp/tq+gc\n9Xq3qz4nPe1y6HRaa4dQqSQ/22bv+YH95yj52b7bmaMUbSGEEMJGSNEWQgghbIQUbSGEEMJGSNEW\nQgghbIQUbSGEEMJGSNEWQgghbIQUbSGEEMJGVOnNVaqi9977P44cOcSFC+nk5+dTv74v7u61mDfv\n7Qq5/tCh9+DjUweNpvTvqfffX37L1/3jj+3ceWcXsrIyWblyGdOnz7zlawohhLi9pGjfoClTngXg\nxx+/48SJeCZPnlrh32PBgsW4uLhU6DXXrl1Nu3Z34O1dWwq2EELYKCnaFWTPnr9Zu/ZzcnNzmTz5\nWaZNm8wPP/wMwMsvT+f++4fTokVL5s17jezsbEwmE1OnvkCzZgHXdf1Bg3r/63p79+4mJ8fAqVOJ\nnD17hqefnkbnzl3ZtOkH1q2LRFEURox4iKKiIg4ejOX555/mxRdf4bXXXmblyv+yZ8/ffPzxMlRV\nQa/34aWXXmXr1ij279/HxYsZnDqVyKhRD3P33UMq7ecmhBDi+tl00Z6942W+i/+mQq95j/8QZneZ\ne1OvjY8/zhdfrMfR0fGKz3/55RfceWcX7rlnCCdPnuDddxfwzjsf3Eq4pKQks2DBYv78cwfffvs1\nrVu34ZNPPuLTT7+gsLCI11+fxfz5i/joow9ZsGAxmZkXLa9dsOANPvvsU3Q6VxYtepMtWzahKArx\n8cf58MNVnDlzmlmzIqRoCyHE5VQVTUoyutj9aM6ehYmP3bZvfV1F++jRozz11FM8+uijjB49usxz\nO3bsYNGiRWi1Wrp3786kSZMAmDdvHjExMSiKQkREBKGhoSQlJTF9+nRMJhN6vZ633377qgXOFjVr\nFnDNfA4c2M/FixlERf0IQEFB/hXbPf/805Z72h4ensyd++ZVrxka2gYAHx8fDAYDCQknadiwMU5O\nzjg5OTN//qIrvi4rKxNFUahXrx6pqdm0a9eBffv20Lx5C4KDQ9Fqtej1PuTkGK4rdyGEsEtGI9rj\nx9DFHUAXewBd7H50cQfQpKWVtmlQF8IG3JZwyi3aubm5zJkzh86dO1/x+blz57Jy5Urq1KnD6NGj\n6devHxcuXCAxMZHIyEji4+OJiIggMjKSxYsXM2rUKAYMGMCiRYtYt24do0aNuungZ3eZe9O94srg\n4OBwxa8bjcaS53U8++wLBAeHXvM65d3TvnQ9AK22dKN6VVXRaLSoqvk6olVQVdXyqKioCEXRXPGa\nQghRHShZmegOxqG9VKDjDqA7fAglv2wHy9SwMQUDO2MMCsbYpi21hj4A6Tm3JcZyi7ajoyMrVqxg\nxYoV/3ru9OnT1KpVi3r16gHQo0cPdu7cyYULFwgPDwfA39+fzMxMDAYD0dHRvPbaawCEhYWxatWq\nWyraVZmiKOSXvNFHjx4BoFWrYH777VeCg0M5efIE0dE7GDFi9LUuc83rXUmjRo05dSqR3NxctFot\nM2Y8y//93xIURYPJZLK0c3d3R1EUzp07h4ODG/v27SE0tE2ZNkIIYZdUFc3ZM6U955ICrU1MKNvM\n0RFji1YYg0MwBodgCgrB2CoItZZHyWVUUvJScFeU2xZ6uUVbp9Oh0125WWpqKl5eXpbHXl5enD59\nmoyMDIKCgsp8PTU1lby8PMvwsbe3N6mpqbcaf5U1ZMhQJk58hMaNmxIY2BKAoUMf5PXXZ/PUU+Mx\nm81Mnfr8LV3vSmrUqMG4cU8wdepTADz44CgURaFt23Y89dQ4Zs6cbWk7ffrLTJs2DbMZfH396N27\nL5s3/3RzCQshRFVUWIj2yOHiXrNliPsAmsvm9wCYvb0p7B5WXKCDgjEGh2JqFgBXGEFNyDzJ18e+\nZN3RSOIvHue7kd9xp2eP25KOol7n+Od7772Hp6dnmXvae/bsYeXKlSxZsgSAr776ylK0e/ToYelt\njxw5knnz5jFq1Ch27twJQGJiIjNmzGDt2rVX/Z5Go6lanMUqhBCiAly4ADExsG9f6b8HD0JRUWkb\nRYGAAGjduvijbVto0wbq1St+7irSc9P5Mu5LPj/wOTtO7wDAWefMfS3u453+7+BT06eyswNucfa4\nj48PaZfdjE9OTsbHxwcHB4cyX09JSUGv1+Pi4kJ+fj7Ozs6WtteSkZF7K+FVCL3ejdTUbGuHUWkk\nP9tm7/mB/eco+d0EsxlNYkLpfeeSHrT27JkyzdQaNTCGtsYYFFrag24ZBK6u/75mWtlJt4WmQpJz\nz7Mn+W++PvolW09txmg2oqDQ3S+Moc2HM6jpPbg5uqOvWbE56vVuV33uloq2n58fBoOBM2fOULdu\nXbZt28aCBQvIyMjgvffeY8SIEcTFxeHj44OrqytdunQhKiqKwYMHs3nzZrp163Yr314IIYS9y8tD\nd/ggurhYy/1n7cE4NIayRdJUpy4FvftgCg4tHd5u0hS0Vx+tTTKc4/ez20kynONczlmScpJIMpwj\nKeccqbkpqJQORAfXDmVo8we5r9kD1HOtX2nplqfcoh0bG8ubb77J2bNn0el0REVF0atXL/z8/OjT\npw+zZ89m2rRpAAwcOJAmTZrQpEkTgoKCGDFiBIqiMGvWLACmTJnCjBkziIyMpH79+gwZIut/hRBC\nFFNSUkrvO5f0oLXHjqKYS1fEqFotpoDmFLYKxhgUgjEkFGNQCKpef0PfKznnPGFfduFC/oUyX3fW\nOlO3Zj061+9K3Zr1aFKrKff630dL71YVkuOtuu572tZQFYaMZOjKtkl+ts/ec6yW+ZlMaE/El1n7\nrI09gDYluUwzs6sbpqDgktnbJT3owJZQo8YtxaSqKqN+GMrPp7bweOtJ9PDrSb2avtRzrYenkxfK\nDc4Gr+j3sNKGx4UQQohrMhjQ/RVtmbWtO3gA3cE4lLy8Ms1Mfg0o6D8QY6vioW1jcAjmho1AU/GH\nUX528GN+PrWFHn5h/KfLvBsu0tYkRVsIIcStU1U055NKdgyLRVvSg+bkCTwvG9BVHRwwBrYs7kEH\nBWMMaV289tnT6xoXrzgnMuOZ9b8Iajl58G6vD2yqYIMU7RuWlHSOMWNGEBjYAoDCwkIeeugRevQI\nu+Frff11JBcvXqR795789tuvjBv3+BXbXTpW82o7rl3uxInjLFr01r+O8+zR405CQlpbHnt7e/Pa\na2/ccMz/tG3bVsLCwjl27Mg1cxBC2JGiIrTHjpZZ96w7eABNenqZZmYPD+jZk9zmJRuUBIVgah4I\nVtq+2mQ2MeXnJ8g15rK052Lqu/paJY5bIUX7JjRs2MhSFLOyMnnssYfo1KkzTk7ON3W9gIBAAgIC\nr/r8pWM1r6doX42rq2uFnMv9T59//ilhYeHl5iCEsE1K5kV0B+Ms9511cbHoDh9EKSws087UuAkF\nne+yzNw2BgVj9vVD7+NOThW5Z79k37v8dT6awf73c3/AMGuHc1OkaN8id/daeHvXJj09nY8/XoFO\n50BW1kX+85/5vPXW65w7dxaj0cj48U/Qvv0d/P33LhYvXoiXlzfe3rWpX9+XPXv+Zv36L5k7961r\nHqv57rtL2bhxA1u3bkJRNHTr1pORI0eTkpLMK6+8iIODA82aNb/u2JOSzvH44y+xbNmnAIwb9zBz\n577JqlXLqV1bz5Ejh0hOPs+rr84lMLAFq1d/yq+//oyiaHjiickcPnyQ48ePEhHxAkOHPmjJ4eef\ntxAZuRqtVktgYEumTn2elSuXXfEYUSFEFaGqaE6fuuxQjNji2dunEss2c3bG2CqoeOZ2cGjx0qpW\nrVDd3K0U+PWJTTvAm7tep45LXd7ssdDmhsUvsemiXXP2yzh9V7FHcxbcM4Sc2dd/CElS0jmysjLx\n8akDFO/pPWPGTDZt+gFv79q89NKrXLx4kWeeeYJPP13LsmXv88orcwgIaM7zzz9N/fqlwzO5uTnX\nPFYzNTWFX3/9mQ8+WAnAk0+OIywsnPXrI+nduy/Dh4/k888/4fjxo7f8cygsLGTRovf55pt1bNr0\nAy4uLvz6688sW/YJ586d5fPPP+HFF19h9epPmTfvbfbs+bskh1yWL1/Cxx+vwcXFhenTn7U8989j\nRKVoC2ElBQXojhxCe9naZ11cLJqszDLNzLX1FPbsVTpzOzgUk38zuMrW1lVVgamASVsnUmQu4p2w\n9/Fy9rZ2SDfNtn7yVcSpU4lMnjwRKD5Q5eWXX7Psz96qVfGe67Gx+4mJ2cv+/fsAKCgooKioiKSk\nJAICinvDbdq0o6CgwHLd8o7VPHQojjNnTjNlSvF949zcHM6fP0dCwknCwoq3jG3btgN//rnjXzEb\nDAZLzAD+/s2ueVhJ69ZtAdDr63DwYBxHjx6hVatgNBoNfn4NePHFV674utOnT+Hn19BySlnbtu05\nevQw8O9jRIUQlU9JT//HsZKxaI8dQbnstEBVUTA1C6Cwd3hJD7r4cAxznbpWjLzivLnrdQ5diGNM\nq7H0btTX2uHcEpsu2jmz595Qr7iiXH5P+590OgfLv2PGjKVPn/5lntdctnzhn0vkyztWU6dzoHPn\nrkyfPrPM11ev/tRyrObVXn+le9rnzyeVeXytIz+1Wg1mc/lL+hWlbF5GYxFOTk5XvKYQogKZzWgT\nTpTcdy6dIKZNOlemmepSE2ObdqVrn4NDMLZoBdc4DtiW/Zm0kyV736WxexNmd606RznfrIpfACeA\n4mM4//hjOwAZGRdYtqz4UJXatfWcOpWAqqrs3bu7zGsuP1azoKCAqVOfQlVVy7GagYEt2bNnN/n5\n+aiqyjvvLKCgIJ+GDRtx+PBBAMtQ9PVwcalJeno6qqqSnp7GuXNnrto2MLAlBw7EYDQauXAhnZde\nKj6h7J+FvEGDRpw5c4rc3OKzZffu3UNgYNXYSUgIu5GTg273Xzh/ugrXF57FY2A4tZv64tWpHbXG\nP0LN/1uA05YoAAr69CPn2efJ/OhTLvy5h7QTZ7n441YMb/0f+WMew9iug00W7DPZp3lr1zxWHljG\n9tPbOGc4+6/OgKEwm8k/P46iKLzXexmuDlfYc9zG2HRPuyrr1SucPXv+4oknxmIymRg7tnhoeuLE\np3j55RnUrVvPch/8kvKO1XzvveUMHz6SSZMmoNFo6N69J05OzgwbNpJXXnmR337bhr9/wHXH6O7u\nTpcuXRg/fgzNmgVcc/Z3vXr16ddvIJMnT0RVVR5/fBIAzZsHMmHCGJ588mlLDpMmPcO0aVNQFA2h\noW1o3boNf/8dfUM/PyEExZPDUpIvm7ld0nuOP45y+dpnrRZT8xbF950v39rT23bv3V7L2ewzDPlm\nIKeyy06Sc9HVJMCzOf4ezQjwbE5s2gFOZSXwdNvnuLNeJytFW7FkG9NyVMstBu2I5Gf77D1HS35G\nI9rjx0pnbsfuRxd3AM1lJyYCmN1rlUwKKx7eNgUFY2zeApxvbslpZavo9y85N5nBG/pzIjOeKW2f\npZV3EMcvHuN4xjGOXTxK/MVjFJhK5woFeYcQNXQbjtrKWxsu25gKIYQdU7Kz0MbFoYvbD8cP4/H3\nnuK1z5dNTAUwNWxEwYBOlo1JjMEhmBs0vOa5z/YsPS+dYRvv5URmPE+3fY6ZnWb9a+mWyWzijOE0\nxzOOkpCVQL/GAyq1YN9uUrSFEKKyqCqas2fKrn2O3Y82MaFMM52jI8YWrTAGBWO6VKCDglFreVgn\n7iroYn4Gw74bzOELh5gY+uQVCzaAVqOlkXtjGrk3vv1B3gZStIUQoiIUFqI9cthypOSl2duazItl\nmpm9vCjs1rNkeDsE926dSPP2hVvY8dDeGQqzGfnDA8Sm7efhVo8xp+t8m90c5VZJ0RZCiBukZFwo\nve98aWnVsSMoRUWWNqqiYGrSlMIeYSW95+LNScx165Ud3ta7gR3fs79VuUW5PPTjcHYn/82w5iN4\nu8f/VduCDVK0hRDi6sxmNIkJJTuGXRrePoD2bNnlkWqNGpYZ25a1zy2DwNX2lxhZU74xn0d+GsnO\nc//jXv/7eLfXB2iU6r1SWYq2EEIA5OWhO3ywTA9aezAOjaFsL9jkU4fCXuFlt/Zs6g+XbR4kbl2h\nqZDxUWPYfmYb/RsPZGn4R+g0UrLkJyCEqHaUlJTS+85xl7b2PIpiLt1RUNVoMAU0pzCodOa2MSgE\n1cfHipFXD4WmQh7fMpbNiZvo2aAXy/t+goNW7vmDFG0hhD0zmdCeiC87czv2ANqU5DLNzK5uGDt0\nLO45h7QuLtCBLaFGDSsFXn3lGfMYt+lhtp7azF2+3fmk/xqcdVVzDbo1SNEWQtgHgwHdoTjLxDDd\nwQPoDsah5OWVaWby9aOg34CSZVUla58bNQZN9b5XWhUYigw88uNIfj+7nV4Nw/m4/2pq6OQPp8tJ\n0RZC2BZVRXM+qfS+86Ue9MkTZbf2dHAo3trzspnbxlZBqF72ubWnrcsqyGTUD8PYdf5PBja5h2V9\nV+GkdbJ2WFWOFG0hRNVVVAQHDuD0207LzG1d3H40Fy6UaWb28KCoa7fSvbeDQzE1DwRH+9kJy55l\n5F/gwe/uY1/qXu4PGMp7vZbJPeyrkKIthKgSlMyL6A7GlR6OEXsA3ZFDUFiI+2XtTI0aU9D5rtKj\nJYOCMfv6VdutPW1dSm4KwzYO5tCFOEa1eJiFPRej1chM/KuRoi2EuL1UFc3pU2W39ow7gPZU2ROb\nVCcnjK2CcGjfjuxmLTAGhWJq1QrVvZaVAhcVLclwjgc23sPxi8cYGzyBed3ervbrsMsjRVsIUXkK\nCtAdOVRy7/nSEqtYNFmZZZqZa9emsEdY6cYkQSGYmgWATode70a+7Bhmd05lJfLAxntIzEpgUptn\neLXzf6r1TmfXS4q2EKJCKOnpl+25fWnt8xEUo9HSRlUUTP7NKOzVu7gwlwxxm33qyPB2NXIm+zSD\nvxnAWcMZXrjjJZ7v8KIU7OskRVsIcWPMZrQJJ0rvO5cUam3SuTLNVBcXjG3aXbYxSXDx1p41a1op\ncFEVpOelM/y7IZw1nCHizleZ2v55a4dkU66raM+bN4+YmBgURSEiIoLQ0FDLc1u3bmXp0qU4Ojoy\naNAgRo8ezVdffcXGjRstbWJjY9m7dy8PP/wwubm5uLi4ADBjxgyCg4MrOCUhRIXJzS1d+3ypF30w\nDiU3p0wzU916FPTugzGkNaagYIzBIZgaN5WtPUUZhsJsRv3wAMcvHuOpNk/zTLtp1g7J5pRbtHft\n2kViYiKRkZHEx8cTERFBZGQkAGazmTlz5rBhwwY8PDyYMGEC4eHhDBs2jGHDhlle/9NPP1mu98Yb\nb9C8efNKSkcIcVNUFU1Kcul950vD2/HHy27tqdViah5YZmMSY1AIau3aVgxe2IICUwGPbhrN3pQ9\njGjxELM6z5Eh8ZtQbtHeuXMn4eHhAPj7+5OZmYnBYMDV1ZWMjAzc3d3x8vICoFOnTuzYsYP777/f\n8volS5awYMGCSgpfCHHDjEa08cdLj5UsKdSatNQyzcxu7hR17FTca75UoANbgrNsKSlujMlsYtLW\nifxWcvjHop7vScG+SeUW7bS0NIKCgiyPvby8SE1NxdXVFS8vL3JyckhISMDX15fo6Gg6duxoabt/\n/37q1auHXq+3fG3x4sVkZGTg7+9PREQEzvILQIhKo2RnoY2LKy7McSU96MOHUPLzy7QzNWhIQf9B\nlp6zMTgEc8NGMjlM3DJVVZnx2zQ2xm+gc/2uLOv7sZzWdQtu+CenXrZNoKIozJ8/n4iICNzc3PDz\n8yvTdt26ddx3332Wx2PGjCEwMJCGDRsya9YsVq9ezbhx4676vTw9XdDprH9PTK93s3YIlUrys216\nvRuoKpw+DTExsG9f8UdMDMTHl23s6AhBQdCmTfFH69YQGorW0xMtUFU3jawW76GdeuWXV/js4Cpa\n12nNTw//QC1n+1xnf7vew3KLto+PD2lpaZbHKSkpZXrOHTt2ZM2aNQAsXLgQX19fy3PR0dG8/PLL\nlsd9+vSxfN6rVy9+/PHHa37vjIzc60ihcun1bqTa8RpRyc8GFRaiPXoEXex+3E8epfCv3ehi96O5\neLFMM7OXF8ZuPcvsvW0KaA4O/9ge0ghU4Z+RXb6Hl7Hn/FbsX8rcP+bS2L0Jnw9YR2G2htRs+8u1\not/Da/0BUG7R7tq1K++99x4jRowgLi4OHx8fXF1dLc+PHz+eN998kxo1arBt2zYee+wxAJKTk6lZ\nsyaOJXv/qqrKY489xuLFi3F3dyc6OpqAgIBbzU0Iu6ZkXLDsGHbp9Crt0cMoRUWWNo6AqXETCi4V\n6Etrn+vWk+FtYTXrjkYy848Z1HWty5f3fEMdlzrWDskulFu027VrR1BQECNGjEBRFGbNmsX69etx\nc3OjT58+DB8+nLFjx6IoChMnTrRMSktNTbV8DsVD6cOHD+fRRx+lRo0a1KlThylTplReZkLYErMZ\nzanEy2ZuF+8cpj1zukwz1dkZY0goxqDiPbfdunUirV5jVFf7HV4VVUueMY93dr/NN8fXU2gqpMhc\nhMlspMhsxGguwmg2UmQuQkXF3bEWUaOjqKdpYu2w7YaiXn6TuoqpCkNG9jx0BZKfVeTlWbb2tGxM\nEheLxlA2TpNPnZI1z8UF2hjSGlNT/zJrn6tkfhXM3nO0pfx+O/MrL2yfysnME7g5uuPp5IlOoyv5\ncECn0eGg0aFVdLg6uvJ8hxcZENLbZvK7WVVqeFwIcfOU1NR/bO15AO3xYygmk6WNqtFgahZAYXCI\npQdtDApBrSPDiaJqSMtLY9b/Ivjq6Fo0iobHW09iRseZuDq4lv9iUaGkaAtREUwmtCdPWNY+X9qk\nRJt8vkwzs6sbxvZ3lFlaZQxsCSW7BApRlaiqSuSRNczeMZML+RcI1bdhYY93ae3T1tqhVVtStIW4\nUQbDZVt7xqKL24/u0EGU3LKrHUx+DSjoN6Ck51x8epW5UWPQyNGDouqLv3iMF7Y/yx9nf8NFV5P/\ndJ3H+JAnZI21lclPX4irUVU055NK7zuX3IPWnohHuWwqiOrggKl5izJLq4xBwaieXte4uBBV1/KY\nD5jz5ywKTAX0bdSf+d0X4ufWwNphCaRoC1GsqAjt8WOXbe1Z3IPWpKeXaWb28KCoazfLfWdjUAim\nwBbFm5YIYQf+e/ATXv7fi/i41OGNbm9zd9PBsuVoFSJFW1Q7SlZm8XKqy9Y+6w4fRCksLNPO1Kgx\nBXd2KVliVbK1p6+frH0WdmtrYhTTtz+Ll7MXG4f8RFOPZtYOSfyDFG1hv1QVEhJw3L6zdAZ33AG0\npxLLNnNywtgqqHRpVVAopqAgVDd3KwUuxO0Xk7KX8VGP4qBx4POBX0rBrqKkaAv7UFCA7ujh4vvO\nJcdK6mIPQFYml+90bK5dm8IeYcUFumQGt6lZAOjkfwVRfSVmJTDqh2HkGXP5uP9qOtTtWP6LhFXI\nbyphc5QL6aX3nS8tsTp2BMVotLRRFQWTfzM0/fthCGiJ6dLWnj51ZHhbiMtcyE9n5PcPkJqXwhvd\n3mZg07utHZK4Binaouoym9EknCw9UrKk96w9d7ZMM9WlJsY27UrXPQeHYGzRCmrWRK93I8/Od2MS\n4mblG/MZ8+NIjl88xqQ2zzAu5HFrhyTKIUVbVA25uegOHyy7tefBODQ5hjLNTPXqUxDet/jEqqBg\njCGhmBo3lbXPQtwgs2pm0s8T2XX+T+5r9gCvdH7N2iGJ6yBFW9x2SnJy8YYksSUbk8QeQBt/HMVs\ntrRRtVpMAc0pDAopc/9ZrV3bipELYT9m7ZjJd/Hf0KX+XSzu/SEaRf7wtQVStEXlMRrRxh//x97b\nsWhSU8o0M7u5U9SxE8bgEEyXZnAHtgRnZysFLoR9WxazhGUxSwj0bMEn/VfjpHWydkjiOknRFhVC\nMWSjjYu77FjJA8Vbe+bnl2lnatCQgv6Dyuy9bW7YSCaHCXEbJBnOMXvHTDYc/5o6LnVZc/c6PJw9\nrR2WuAFStMWNUVU0585e1nsu7kFrE06WbebggDHw0qztkiHuVkGoHvILQojbrchUxPL9S1nw93xy\nigy082nPu72W0sCtobVDEzdIira4usJCtMeOlm7tebB4iZUmI6NMM7OnJ4XdepTO3g4KwRTQXLb2\nFKIK+OPsb7z02/McyTiMl7MXc7u+z8iWo+Ueto2Soi0AUC5mlK57jost3qTkyCGUoqIy7YxNmlJ0\nV4+SgzFK1j7Xqy/D20JUMZcPhSsoPBo0jpfufAVPZznIxpZJ0a5uVBVNYoKlQHPsEF579qI9c7ps\nsxo1SvbcDrWcXGVq1QrV1c1KgQshrkdWQSafHfyEhX+/SU6RgfZ1OjC/20I5A9tOSNG2Z/n56I4c\nKr3vHBdbPHs7O6tsO586FPYKv2xzklBMTf1Bq7VO3EKIGxJ/8RibE6LYkriJP5N2YDQb8Xb2Zm7X\n+TIUbmekaNsJJS3tsl3Dimdwa48dRTGZLG1UjQZTswAK+/TF2CoEY0goHj06c0HjYsXIhRA3qtBU\nyJ9JO9iSsIktiVGcyIy3PNfWpx19Gw9gbPAEGQq3Q1K0bY3JhDbhhGXmtvbSPejzSWWamWu6Ymx/\nR5mlVcYWraBGjbLX07uBbPMphM1YvOf/eGf3AgxFxf/f1nRwZVDTe+nbqD+9GvWhjksdK0coKpMU\n7aosJwfdobiyh2McikPJzS3TzOTrR0Hf/iUFuvgetLlxE9naUwg788G+95j75yx8XOowquVowhv1\no3P9rrI5SjUiRbsqUFU0yee7guhxAAAgAElEQVRL7ztfugd9Ih5FVUub6XSYmrconhgWElrcgw4K\nRvXytmLwQojbYfXBz5i9Yyb1atbnu/uiaOjeyNohCSuQon27FRWhPX6szKlVurj9aNLTyzQz1/Kg\nqMtdpcPbQSGYmgeCk/xFLUR18138N0zb/jRezl58dc+3UrCrMSnalUjJykR3MK74vvOl3cOOHEIp\nKCjTztSwMQV3dindOSwoGLNfA1n7LITgl1NbeWLLOFx0NVl793qaewVaOyRhRVK0K4Kqojlzusyx\nkrrYA2hPJZRt5uSEsUUry8Ykpktbe7rXsk7cQogqbVdSNGM3FS/Z+u/AtbTxaWftkISVSdG+UQUF\n6I4eLt4x7FKBjotFk3mxTDOztzeFPcLKrn1uFgA6+ZELIcoXm3aAUT8MpcBUwCcD1tDVt5u1QxJV\nwHVVkHnz5hETE4OiKERERBAaGmp5buvWrSxduhRHR0cGDRrE6NGjiY6O5plnniEgIACA5s2b88or\nr5CUlMT06dMxmUzo9XrefvttHKvw/tTKhXQ48Bc1/oi27L+tPXYExWi0tFEVBZN/Mwp79iruPZfs\nHmauU1eGt4UQN+XExeMM/24I2YVZLAlfTr/GA6wdkqgiyi3au3btIjExkcjISOLj44mIiCAyMhIA\ns9nMnDlz2LBhAx4eHkyYMIHw8HAAOnbsyOLFi8tca/HixYwaNYoBAwawaNEi1q1bx6hRoyohrRtk\nNqNJOFk8MSyu9P6z9txZAFxLmqkuLhhbt8EY3LpkglgwxpZBULOm9WIXQtiVc4azDN04mLS8VOZ3\nX8jQ5g9aOyRRhZRbtHfu3GkpxP7+/mRmZmIwGHB1dSUjIwN3d3e8vIp33enUqRM7duzA19f3iteK\njo7mtddeAyAsLIxVq1bd/qKdl4fu8EHLsipdXCzauFg0OYYyzUx161EQ3henO9qT1TSwuBfduKls\n7SmEuCXZhVmcyjrF+ZxzJOUkkaWmczzlJEkljxOzEsgpMvBSx1cYGzzB2uGKKqbcop2WlkZQUJDl\nsZeXF6mpqbi6uuLl5UVOTg4JCQn4+voSHR1Nx44d8fX15fjx4zzxxBNkZmYyefJkunbtSl5enmU4\n3Nvbm9TU1MrL7J+Kiqg19F4coneimM2WL6taLaaA5hQGlc7cNgaHotauDYBe70aB7BgmhKgAf5z9\njdE/DCfXmHvF510d3Khfsz4PthjFlLbP3ubohC244VlR6mWbfSiKwvz584mIiMDNzQ0/Pz8AGjdu\nzOTJkxkwYACnT59mzJgxbN68+arXuRpPTxd0ugrq2ebng5MDdO0KbdpA69bQpg1KUBA6Z+dr/iD0\nevs+2Urys232nh/YR47puelM+eVxCs2FPN7+cRq4N8DP3Q9fd1983XzxdffF3cnd2mFWCnt4/8pz\nu3Ist2j7+PiQlpZmeZySkoJer7c87tixI2vWrAFg4cKF+Pr6UqdOHQYOHAhAw4YNqV27NsnJybi4\nuJCfn4+zszPJycn4+Phc83tnZFz5r9Gb9uXGf38tu6j44yr0ejdS7binLfnZNnvPD+wjR1VVGRs1\nlrPZZ5l55yyeaT/N8tyl/AqyIBXbzvNK7OH9K09F53itPwDK3Zy6a9euREVFARAXF4ePjw+urq6W\n58ePH096ejq5ubls27aNzp07s3HjRlauXAlAamoq6enp1KlThy5duliutXnzZrp1kyUMQgj7t+bQ\nf/nhxEY61+/K5LZTrR2OsGHl9rTbtWtHUFAQI0aMQFEUZs2axfr163Fzc6NPnz4MHz6csWPHoigK\nEydOxMvLi169evH888/z888/U1RUxOzZs3F0dGTKlCnMmDGDyMhI6tevz5AhQ25HjkIIYTXxF48x\n84/puDvWYknv5Wg1MplV3DxFvZ6by1ZSFYZU7H1oR/KzbfaeH9h2jkWmIgatD2df6l6W9/mYIQEP\n/KuNLed3Pew9P6hiw+NCCCFuztt/vcG+1L0MDxx5xYItxI2Soi2EEJVg57n/8e6ehTR0b8wb3d62\ndjjCTkjRFkKICpZZcJGntk5Ao2hYGr4CN0f7XMolbj8p2kIIUYFUVeWF7VM5azjDcx2mc0fdO60d\nkrAjUrSFEKICfXnkC745vp476t7Js+1fsHY4ws5I0RZCiApyIjOeF39/HlcHNz4IX4FOI0fxiool\nRVsIISrAtlM/M+jrcHKKDMzvvoBG7o2tHZKwQ1K0hRDiFpjMJt7aNY8R399PdmE2b3ZfxPDAkdYO\nS9gpGbsRQoiblJaXxlNbx/Pr6V9o4NaQj/p+Sts67a0dlrBjUrSFEOIm/HU+mglRj3Iu5yx9GvXj\n/d7L8HT2snZYws7J8LgQQtwAVVVZHvMBg78ZwPncJGbeOYv/DoyUgi1uC+lpCyHEdcouzGLqtsl8\nF/8NtWvoWd73Y+7y7W7tsEQ1IkVbCCGuQlVVDl04yG9ntrH99DZ2nvsfucZcOtXrwvK+H1O3Zj1r\nhyiqGSnaQghxmSTDObaXFOnfzvxKal6K5bnmnoHcHzCMp9s9J2uwhVXIf3VCCAHsTd7NC789y/7U\nfZav+bjUYWjzB+nu15MefmHUc61vxQiFkKIthKjmikxFLNr9Fu/sXoBJNdGrYTg9G/Siu18YLb1a\noSiKtUMUwkKKthCi2jp64QiTfp5ITOpe/FwbsLj3UplYJqo0KdpCiGrHrJr5aP+HzP1zNvmmfEa0\neIi5Xefj7lTL2qEJcU1StIUQ1cqZ7NM888tT/H52O97O3izts5JBTe+xdlhCXBcp2kKIakFVVb46\nupaXfn+B7MIs+jUewMKe7+Hj4mPt0IS4blK0hRB27VRWIl8dXcuXR77gZOYJXB3ceDfsA0a0eEgm\nmQmbI0VbCGF3DIXZfBf/LZFH1rDj3B8A1NDVYGjzB3mx48s0dG9k5QiFuDlStIUQdsGsmvn9zHYi\nj6zhxxPfkWvMBaBL/bt4MHAU9/gPxtXRzcpRCnFrpGgLIWxeTlEOj/40iu1ntgHQ2L0JwwNHMixw\nBI3cG1s3OCEqkBRtIYRNyy7MYtQPw4hO2knPBr14rsMM7qzbSe5XC7skRVsIYbMy8i8w4vv72Zuy\nhyHN7mdJ7xU4aB2sHZYQlUaKthDCJqXlpTFs42Di0g8wosVD/F/P99FqtNYOS4hKdV1Fe968ecTE\nxKAoChEREYSGhlqe27p1K0uXLsXR0ZFBgwYxevRoAN566y12796N0Wjk8ccfp2/fvrz44ovExcXh\n4eEBwLhx4+jZs2fFZyWEsGvnc5IYuvFejmYc4dGgcczvvhCNorF2WEJUunKL9q5du0hMTCQyMpL4\n+HgiIiKIjIwEwGw2M2fOHDZs2ICHhwcTJkwgPDychIQEjh07RmRkJBkZGdx333307dsXgOeee46w\nsLDKzUoIYbdOZ5/igW/vISHrJE+0nsxrXV6X+9ei2ii3aO/cuZPw8HAA/P39yczMxGAw4OrqSkZG\nBu7u7nh5eQHQqVMnduzYweDBgy29cXd3d/Ly8jCZTJWYhhCiOjiZeYIHvr2HM4bTPNdhOjPumCkF\nW1Qr5Y4npaWl4enpaXns5eVFamqq5fOcnBwSEhIoKioiOjqatLQ0tFotLi4uAKxbt47u3buj1Rbf\na/r8888ZM2YMzz77LBcuXKiMnIQQdujohSPcu6E/ZwynmXnnLF7s+LIUbFHt3PBENFVVLZ8risL8\n+fOJiIjAzc0NPz+/Mm23bt3KunXrWLVqFQCDBw/Gw8ODli1bsnz5ct5//31effXVq34vT08XdDrr\nTyzR6+17QwbJz7bZc35ZBVn8N+a/RMZFsjl+M0XmIt7p9w7PdHrG2qFVKHt+D8H+84Pbl2O5RdvH\nx4e0tDTL45SUFPR6veVxx44dWbNmDQALFy7E19cXgN9//50PP/yQjz76CDe34mQ6d+5seV2vXr2Y\nPXv2Nb93Rkbu9WdSSfR6N1JTs60dRqWR/GybPeaXU5TD5oSf+Ob4en45tYUCUwEAwbVDmdz2Ge73\nH2ZXOdvje3g5e88PKj7Ha/0BUO7weNeuXYmKigIgLi4OHx8fXF1dLc+PHz+e9PR0cnNz2bZtG507\ndyY7O5u33nqLZcuWWWaKA0yZMoXTp08DEB0dTUBAwE0nJYSwHwWmAr6P38j4qEdo9XFTHt8ylp9O\nfk+TWk35T8//sHPUbn4Z/gf3BwyzdqhCWFW5Pe127doRFBTEiBEjUBSFWbNmsX79etzc3OjTpw/D\nhw9n7NixKIrCxIkT8fLysswanzp1quU6b775Jg899BBTp06lRo0auLi48MYbb1RqckKIqktVVf46\nv4svj3zBt/HrySy4CIC/RzMGN7ufIc0eoIVXy2rRUxPieinq5Tepq5iq8D+qvf/CkPxsmy3ml5B5\nkq+OruWrI2tJyDoJQB2XujzQfDgPNB9OsHdImQlmtpjjjZD8bN/tHB6XHdGEEJWu0FRI5JE1fHnk\nC6KTdgLgonNhaPMHGR44km6+PWQ3MyGugxRtIUSle+7XKXx55AsUFLr59WR48xEM8r8XVwfX8l8s\nhLCQoi2EqFRbEjbx5ZEvaKNvy8f9V+Pr5lf+i4QQVySb9QohKk1mwUWmbX8GB40D7/ZaKgVbiFsk\nRVsIUWlm73iZ8zlJTOswg5berawdjhA2T4q2EKJS/Hr6F1Yf+ozg2qFMafustcMRwi5I0RZCVDhD\nYTbTfn0araLl3bAlOGgdrB2SEHZBirYQosLN+XMWp7NP8XS7ZwnRt7Z2OELYDSnaQogKtePsH3wc\n+xGBni14rsMMa4cjhF2Roi2EqDC5RblM3TYJjaLhnV5LcNI6WTskIeyKFG0hRIV5Y9ccErJO8kTr\nybSvc4e1wxHC7kjRFkJUiL/OR7M85gOa1vJnRseZ1g5HCLskRVsIccvyjflM/WUSAO/0+oAauhpW\njkgI+yRFWwhxSwpNhcz8YwbHLh5lXMhEOtXrbO2QhLBbsve4EOKm/XU+mmm/Ps3hC4fw92hGRKdZ\n1g5JCLsmPW0hxA0zFGYT8fsL3L2+L4cvHOLRoHFEPbBNTu0SopJJT1sIcUO2JkYxfftznDGcpplH\nAIt6vken+l2sHZYQ1YIUbSGqOaPZyN6U3bg5ulOvZj3cHWuhKMq/2qXlpfHyH9NZf2wdOo2O59q/\nwNT2L+Csc7ZC1EJUT1K0haimCkwFfHnkCxbvWURiVoLl6y46F+q51qdezfrUrVmP+jV9qeFQgxX7\nl3Ih/wLtfNqzKOx9WnkHWS94IaopKdpCVDN5xjxWH/yU9/e+y7mcszhpnRjZYjQOGkfO55wjKSeJ\npJyzxF88XuZ1LjoX5nadz7iQx9FqtFaKXojqTYq2ENWEocjAp7Gr+GDfYlLzUnDRufBE68k81WYK\ndWvW+1f7AlMB53OSSMpJIjU3mXY+HfB187NC5EKIS6RoC2HnDIXZLN+/lGUxS8goyMDVwY2p7Z5n\nYuunqF2j9lVf56R1opF7Yxq5N759wQohrkmKthB2LKsgk/u+vZsDaTF4OHkw/Y4Ixoc8joezp7VD\nE0LcBCnaQtip3KJcHvpxOAfSYhjR4iHm3fUWro5u1g5LCHELpGgLYYcKTAU8tukhopN2MqTZ/fxf\nz/dl8pgQdkB2RBPCzhjNRp7cMp5tp3+mT6N+LOm9Qgq2EHZCirYQdsSsmpn269N8f+JbutS/i4/6\nfYaD1sHaYQkhKsh1DY/PmzePmJgYFEUhIiKC0NBQy3Nbt25l6dKlODo6MmjQIEaPHn3V1yQlJTF9\n+nRMJhN6vZ63334bR0fHyslMiGpGVVVe/d9LfHH4c9r6tOO/A9fKEZlC2Jlye9q7du0iMTGRyMhI\nXn/9dV5//XXLc2azmTlz5rBixQpWr17Ntm3bOH/+/FVfs3jxYkaNGsWaNWto1KgR69atq7zMhKhm\n3v7rDZbvX0qgZwu+uPtr3BzdrR2SEKKClVu0d+7cSXh4OAD+/v5kZmZiMBgAyMjIwN3dHS8vLzQa\nDZ06dWLHjh1XfU10dDS9e/cGICwsjJ07d1ZWXkJUKx/GvM+Cv+fTyL0xX937LV7O3tYOSQhRCcot\n2mlpaXh6lq7p9PLyIjU11fJ5Tk4OCQkJFBUVER0dTVpa2lVfk5eXZxkO9/b2tlxHCHFzVFVlVewK\nXv1fBHVr1mPdvRuvuLuZEMI+3PCSL1VVLZ8risL8+fOJiIjAzc0NP78rb3F4+Wuu9bV/8vR0Qaez\n/qxXvd6+17ZKfrYp5nwMwz+byq8Jv+Jdw5ufH9lKK30ra4dVKez1PbxE8rN9tyvHcou2j48PaWlp\nlscpKSno9XrL444dO7JmzRoAFi5ciK+vLwUFBVd8jYuLC/n5+Tg7O5OcnIyPj881v3dGRu4NJ1TR\n9Ho3UlOzrR1GpZH8bE9aXhrzo+fy+aFPMKtm+jbqz3/uegM9DewuV7DP9/Bykp/tq+gcr/UHQLnD\n4127diUqKgqAuLg4fHx8cHV1tTw/fvx40tPTyc3NZdu2bXTu3Pmqr+nSpYvl65s3b6Zbt263lJgQ\n1UmhqZAPY96n0+q2fHZwFc08Atj00CY+H/QlTWv5Wzs8IcRtUG5Pu127dgQFBTFixAgURWHWrFms\nX78eNzc3+vTpw/Dhwxk7diyKojBx4kS8vLzw8vL612sApkyZwowZM4iMjKR+/foMGTKk0hMUwh5s\nTYzilf+9RPzF49Ry8mDeXW/xSNA46tf1svtejBCilKJez81lK6kKv4zsfWhH8qvaLuZn8NTWCWw9\ntRmNouHRoHFM7xhhmR1u6/ldD3vPUfKzfbdzeFz2HheiijIUGRj5w1B2J/9FN98ezLlrPq28g6wd\nlhDCiqRoC1EF5RvzeeSnUexO/ouhzR/k/d7L0Ciy67AQ1Z38FhCiiikyFTFx86P8fuZX+jcZxOJe\nS6VgCyEAKdpCVClm1cyUX55gU8KPdPcLY3mfj9FpZEBMCFFMirYQVYSqqsz4bRrrj33FHXXv5NMB\na3DWOVs7LCFEFSJFW4gqQFVV/rPzVT6NW0lw7VDWDPqKmg41rR2WEKKKkaItRBXwzu4FLNn3Ls08\nAoi8ewO1nDysHZIQogqSoi2ElX20/0Pe2DWHBm4NWXfvRvQu+vJfJISolmSGixCVyGg2cjTjCKm5\nKaTkJpOal1r8b24KqXkppOSmcDA9Fh+XOnx177fUd/W1dshCiCpMirYQlaTIVMQDG+/hz6QdV23j\n6uBGa31bFvdaKvuHCyHKJUVbiEry7p6F/Jm0g871u9LNtwc+LnXQu/igr6Ev+dcHFwcXa4cphLAh\nUrSFqAT7Uvaw8O83qV/Tl88GfCETy4QQFUImoglRwfKMeUzaOhGTamJx76VSsIUQFUaKthAVbO7O\nWRy7eJSJoU/S3a+ntcMRQtgRKdpCVKDtp7ex4sCHNPcMZGan2dYORwhhZ6RoC1FBMgsu8swvT6HT\n6FjSezk1dDWsHZIQws5I0Raigrz42/OcyznLtA4zaO3T1trhCCHskBRtISrAxuMb+PrYl7Tzac8z\n7aZZOxwhhJ2Soi3ELUrOOc8L26dSQ1eDJeHL5ShNIUSlkd8uQtwCVVWZum0SGQUZvNFtAf4eAdYO\nSQhhx6SnLcQt+Ozgx/x8ags9G/RibPAEa4cjhLBz0tMW4gaoqsrRjCNsOvkDP538nj0pu/Fw8uDd\nsA9QFMXa4Qkh7JwUbSHKYTKb+Dv5L346+T2bTv7Aicx4ALSKlm6+PXj+jhep51rfylEKIaoDKdpC\nXIHJbOJ/535nw7F1RCX8SFpeGgAuuprc4z+E/o0HEt6oL57OXlaOVAhRnUjRFuIyB9Pj+OrIWtYf\n+4qknHMA1K6h5+FWj9K/8UC6+fXEWeds5SiFENWVFG1R7SUZzrH+2Dq+OrqWg+mxALg71uLhVo/y\nQMBw7qzXGa1Ga+UohRBCiraoxnYlRfPWX/P4/cyvqKg4aBzo32QQw5qPoE+jftKjFkJUOddVtOfN\nm0dMTAyKohAREUFoaKjludWrV7Nx40Y0Gg3BwcHMnDmTpUuXsmPHDgDMZjNpaWlERUXRq1cv6tat\ni1Zb3GtZsGABderUqYS0hLi27+K/4ckt4yk0F9KhTkeGBY5gcLP78HL2tnZoQghxVeUW7V27dpGY\nmEhkZCTx8fFEREQQGRkJgMFgYOXKlWzevBmdTsfYsWPZt28fTz75JE8++SQAGzZsID093XK9FStW\nULNmzUpKR4jyrTywjIjfp+PiUJP/DowkrGFva4ckhBDXpdzNVXbu3El4eDgA/v7+ZGZmYjAYAHBw\ncMDBwYHc3FyMRiN5eXnUqlXL8lqj0cgXX3zB6NGjKyl8Ia6fqqrM3Tmbl35/gdo19Hw75Ecp2EII\nm1JuTzstLY2goCDLYy8vL1JTU3F1dcXJyYlJkyYRHh6Ok5MTgwYNokmTJpa2mzdv5q677sLZufTe\n4KxZszh79izt27dn2rRpsiGFuC2KTEU8++tkvjzyBU1r+bP27vU0rtWk/BcKIUQVcsMT0VRVtXxu\nMBhYtmwZmzZtwtXVlUceeYTDhw/TokULAL7++mtee+01S/unn36abt26UatWLSZNmkRUVBT9+/e/\n6vfy9HRBp7P+rF293s3aIVQqe8+vRi2Fh78cRVR8FB19O/L9yO/R19RbO6wKY+/vH9h/jpKf7btd\nOZZbtH18fEhLS7M8TklJQa8v/oUXHx9PgwYN8PIq3mCiQ4cOxMbG0qJFC3Jzczl//jx+fn6W1w4Z\nMsTyeffu3Tl69Og1i3ZGRu6NZ1TB9Ho3UlOzrR1GpbH3/Mw1cun32QBiUvcS3rAvK/p9CrnOpOba\nR872/v6B/eco+dm+is7xWn8AlHtPu2vXrkRFRQEQFxeHj48Prq6uAPj6+hIfH09+fj4AsbGxNG7c\nGIDDhw/TtGlTy3Wys7MZN24chYWFAPz1118EBMiJSKLynMiMp+uqrsSk7mVUi4f5bOBaajrIJEgh\nhO0qt6fdrl07goKCGDFiBIqiMGvWLNavX4+bmxt9+vRh3LhxjBkzBq1WS9u2benQoQMAqamplh44\ngJubG927d+fBBx/EycmJVq1aXbOXLcTN2pP8NysPLGdj/AYKTAU81/4FZnR8WeZPCCFsnqJefpO6\niqkKQyr2PrRjL/nlGfP49vh6Vh1Yzr7UvQD4ezRjdtgs+tUbbOXoKo+9vH/XYu85Sn6273YOj8uO\naMKmJWYl8EnsStYc+oyMggw0iob+TQYxNngC3f16Usenlt3/whBCVB9StIVNyirI5OlfnuKnk9+j\nouLt7M3TbZ/jkeCxNHBraO3whBCiUkjRFjanyFTEuKgxbD+zjbY+7RgX8jj3+t8ne4ULIeyeFG1h\nU1RV5aXfX2D7mW30azyAT/qvkRO4hBDVRrlLvoSoSpbtX8JnB1cRXDuUpX1WSsEWQlQrUrSFzdh0\n8kdm/W8mdVzq8vnASFwdXK0dkhBC3FZStIVNOJAawxNbxlJDV4PPB0ZS39XX2iEJIcRtJ/e0RZWX\nZDjH6B8fJM+Yx8f9V9Pap621QxJCCKuQnrao0gxFBkb/+CBJOed4tfMcBja929ohCSGE1UjRFlWW\nyWziqS3jOZAWw8OtHuWpNlOsHZIQQliVFG1RZf1n56tsSviRbn49md9toewdLoSo9uSetqhSVFUl\n+vyffLT/QzbGbyDAozmr+n2Gg9bB2qEJIYTVSdEWVUKeMY/1R79iZexyYtP2AxBcO5RV/f5LLScP\nK0cnhBBVgxRtYVWns0/xcexHrD74KRkFGWgVLff4D2F8yON0qtdFhsSFEOIyUrTFbaeqKjvO/cHy\n/UuJSvgRs2rG29mbqe2e55Ggsfi6+Vk7RCGEqJKkaIvbpsBUwIZj61gW8wFx6QcAaK1vy7iQiQxp\n9oAc+CGEEOWQoi0qXUpuCp/GreTj2I9Iy0tFq2gZ7H8/E0Kf5I66HWUIXAghrpMUbVFpYtMOsGL/\nUr4++iWF5kJqOXkwqc0zjAuZiJ9bA2uHJ4QQNkeKtqhw2YVZPLFlHFsSowBoWsufCaFP8mCLUXLI\nhxBC3AIp2qJCZRVk8uD397M7+S861evC5LbPEN6oHxpF9vERQohbJUVbVJjign0fu5P/ZljzESzu\ntVTOuxZCiAok3R9RITILLjL8uyHsTv6b4YEjpWALIUQlkKItbtmlgr0nZTcPBo7i3bAPpGALIUQl\nkKItbsnF/AyGbRzM3pQ9jGwxmnfClkjBFkKISiL3tMVNu5ifwbDvhhCTupdRLR5mUdh7MuFMCCEq\nkfyGFTclI/8CQ78bTEzqXh5qOUYKthBC3AbyW1bcsAv56QzdOJj9qfsY3fIRFvZcLAVbCCFug+sa\nHp83bx4xMTEoikJERAShoaGW51avXs3GjRvRaDQEBwczc+ZM1q9fz7vvvkvDhg0B6NKlC08++SSH\nDx9m9uzZAAQGBvLaa69VfEaiUiUZzjH8uyEcyTjMw60e5e0e70jBFkKI26Tcor1r1y4SExOJjIwk\nPj6eiIgIIiMjATAYDKxcuZLNmzej0+kYO3Ys+/btA2DgwIHMmDGjzLVef/11S9GfNm0a27dvp0eP\nHpWQlqgMJzNPMGzjYE5lJ/J46FO81nWeFGwhhLiNyv2Nu3PnTsLDwwHw9/cnMzMTg8EAgIODAw4O\nDuTm5mI0GsnLy6NWrVpXvE5hYSFnz5619NLDwsLYuXNnReUhKllcWiz3bOjHqexEZnScyX+6viEF\nWwghbrNyf+umpaXh6elpeezl5UVqaioATk5OTJo0ifDwcMLCwmjdujVNmjQBinvo48aN45FHHuHg\nwYNkZGTg7u5uuY63t7flOqJq++t8NEO+HUhKbjLz7nqLaR1myMlcQghhBTe85EtVVcvnBoOBZcuW\nsWnTJlxdXXnkkUc4fPgwrVu3xsvLi549e7J3715mzJjBRx99dNXrXI2npws6nfXX/Or1btYOoVJd\nK78t8VsY9t0QCowFfPzcUAYAABSHSURBVDbkMx5u/fBtjKxiVOf3z17Ye46Sn+27XTmWW7R9fHxI\nS0uzPE5JSUGv1wMQHx9PgwYN8PLyAqBDhw7ExsYydOhQ/P39AWjbti0XLlzA09OTixcvWq6TnJyM\nj4/PNb93RkbujWdUwfR6N1JTs60dRqW5Vn7fxX/LE1vGolE0rOr/Of3rD7K5n0V1fv/shb3nKPnZ\nvorO8Vp/AJQ7PN61a1eiooqPWIyLi8PHxwdX1+LjFX19fYmPjyc/Px+A2NhYGjduzIoVK/j+++8B\nOHr0KF5eXjg6OtK0aVP+/vtvADZv3ky3bt1uLTNRab449DkTNj+Co9aJL+7+mgFNBlk7JCGEqPbK\n7Wm3a9eOoKAgRowYgaIozJo1i/Xr1+Pm5kafPn0YN24cY8aMQavV0rZtWzp06ICfnx8vvPACa9eu\nxWg08vrrrwMQERHBq6++itlspnXr1nTp0qXSExT/Fp30J9tObyW3KBdVV0RaVga5xlxyi3LINeaS\nU5TDwfRYPJ08WXv3etrWaW/tkIUQQgCKej03l62kKgyp2NvQzr6UPQxa34cic9EVn9cqWlwcatLI\nvTEfhK+ghVfL2xxhxbK39++f7D0/sP8cJT/bdzuHx2Xv8WokqyCTCZsfxWg28m7YB7T0boWfjw/5\n2SouDi7UdHDFUeMoM8OFEKKKkqJdTaiqyrO/TiExK4Fn2z/PyP9v796jsqrzPY6/uV8EjUcBL8jR\nPCkm6TKx8TJeAyfTozNTx8mJgMTTTa2pU6KgYs2kecmVhqkpNU5ROiLjUDlCjjanglAbw8AxhZkG\nMi/gHSEV+J0/HJ+RVBQSNg98Xmuxls9lb74ff+z93fu3Nw89I4F/HSHSvI+CRUSaC306RgvxZv4a\n3ivcxIAOg3iuf7zV5YiISD2oabcAX5bkMueTmbT1bMuqiDdwddYEi4iII1LTbubOnD/N5Mxozlef\nZ3n463Tw6Wh1SSIiUk9q2s2YMYb//ehJ/nHq70zr+zQjgyOsLklERH4ANW0H89mhbJ7Pms22oq1U\nm+pa3/u7vW+yqSCN/u1/xIy7ZjVShSIi0lB0cdNBFJ8p4oWsOfyxMA2A5V8spbNvMBNDIpkYEkkn\n36Aa788r/ZJZn8Th5+HH6xFv4ubiZkXZIiJyE+lMu4k7e+EsL+X8msHvhPHHwjTuDOjH6lG/JbJn\nNMcqjrFw5zz6vR3KL9+/nw/+/h4Xqi5Qdv4M/5MZzbmqc7x698orGrqIiDgmnWk3UdWmmtT96/nN\nZ3M5fPYQ7Vt1YNaAudzf/Rc4Ozkz/j9/zguD57GpII2Uv61la1EmW4syaeflT7BvMIUnC3i8zzRG\ndRltdRQREblJ1LSboF2HdzD70xl8fmQXni6ePNPvOabe+TQ+bj413ufj7kvk7dFE3h7N3mP5pOxd\ny4b96/jr0c/pFxjGrAFzrQkgIiINQk27CTHGkJiVwMrcJADGd/s5cwa9QGff4Osue3vbXrw4ZCGz\nB77Apwf/j36B/XUdW0SkmVHTbiKMMczNmsXK3CS6+/Vg8bClDOhY97+C5unqyd3/MaoBKhQREaup\naTcRC3fOY0Xuq3T368Efxm/G39vf6pJERKSJ0d3jTcCyvy7h5V0L6NK6K6nj0tWwRUTkqtS0LbZ6\nzwp+89lcgnw6s3H8e7Rv1cHqkkREpIlS07bQW3t/S8IncQR6tyd1fPoN3XAmIiItl5q2RTZ8tY5n\nP3qKdl7t2DjuPW5t083qkkREpIlT07bAe4WbmLbtMVp7tOH3//VHutt6WF2SiIg4ADXtRvbh11t4\n9MNJeLu2Yv3YNELb3WF1SSIi4iDUtBvRHw6kErPlQdyd3XlnbCp3BoZZXZKIiDgQNe1GsjI3iUc/\nnISnqxcpYzYwoMNAq0sSEREHow9XaWDVptr+SWftW3Xg3TEb6dUu1OqyRETEAalpN6BzVed4atvj\npB1IpbtfD9aNTSPIt7PVZYmIiINS024gZ86fJuZPD/Lxwb/Qv/2PePve9fh52qwuS0REHJiadgM4\nfPYQE9+/n/xjXzK661hWRiTj5epldVkiIuLgdCPaTXbgxH7GpEWQf+xLYnrF8sZP3lLDFhGRm+KG\nzrTnzZtHbm4uTk5OxMfH07t3b/trKSkppKen4+zsTGhoKAkJCVRWVpKQkEBRURFVVVVMnz6dsLAw\nHnroIcrLy/H29gYgLi6O0FDHvinryNnD5JXu4ct/ff2leDunz59i5l2z+VW/Z3FycrK6RBERaSau\n27R37NjBP//5T9avX09hYSHx8fGsX78egLKyMpKTk8nMzMTV1ZVJkybxxRdfUFhYiJeXF++++y4H\nDhxg5syZpKamAjB//ny6d+/esKkayLmqc2T8YzN7SnL5sjSXvNIvKak4WuM9Nk8by0au4IGQBy2q\nUkREmqvrNu3s7GzCw8MB6NatG6dOnaKsrAwfHx/c3Nxwc3Oznz1XVFTQpk0bxo0bx9ixYwGw2Wyc\nPHmyYVM0gmpTTcyffsmfiz60Pxfk05l7uo4htO0d3OHfhzva9aaTT5DOrkVEpEFct2mXlpbSq1cv\n+2ObzUZJSQk+Pj54eHgwZcoUwsPD8fDwYMyYMXTt2rXG8mvXrrU3cIBly5Zx4sQJunXrRnx8PJ6e\nnjcxTsNJ2r2UPxd9yJBOw/hVv2cJbXeH7gYXEZFGVee7x40x9n+XlZWxatUqtmzZgo+PD9HR0ezb\nt4+QkBDg4vXu/Px8Vq5cCUBUVBQ9evQgODiYxMREUlJSiI2Nveb38vPzxtXVpa4l3nT7K/YwP+cF\nOvp2ZOPEDfi38re6pJvK39/X6hIalPI5vuaeUfkcX2NlvG7TDggIoLS01P746NGj+PtfbFqFhYV0\n7twZm+3iGWdYWBh5eXmEhISwYcMGtm3bxmuvvYabmxsAERER9vWMHDmSzZs31/q9T5wor3uim8y5\n1Xkm/P4XGAwr7k6Gck9Kys9YXdZN4+/vS0lJ88nzfcrn+Jp7RuVzfDc7Y20HANf9la/BgweTkZEB\nQH5+PgEBAfj4+ADQqVMnCgsL+e677wDIy8ujS5cuFBcXs27dOpKSkvDw8AAunqHHxMRw+vRpAHJy\ncrjtttt+WLIGVm2qid4UzbdnDxLXP4GBHQdbXZKIiLRg1z3TvvPOO+nVqxcPPPAATk5OJCYmkpaW\nhq+vLxEREcTGxhIVFYWLiwt9+/YlLCyMJUuWcPLkSR555BH7epKTk5kwYQIxMTF4eXkRGBjItGnT\nGjTcD7XiiyQ+OPABw4JG8FS//7W6HBERaeGczOUXqZsYK6dUdh3ewbhN9+Dv7c/W+z/B37t5Xce+\npLlPXSmf42vuGZXP8TWp6fGW6MR3x3kk82GqTTXv3PdOs23YIiLiWNS0v8cYw1PbnuCbsmKeDZvB\n8C7DrS5JREQEUNO+wqo9y9ny9WaGdBrG0/2es7ocEREROzXty/z1yC5+nZ2Iv1cAr0WswcXZ+t8R\nFxERuURN+18+PfgxkZsnUFldyYqINQR6B1pdkoiISA0tvmkbY1jxRRL3p4/j5LmTLBr2CkODhltd\nloiIyBXq/DGmzUnZhTKe2T6VTQVpBHgHkvyTt/hRhwFWlyUiInJVLbZp//1kAQ9vieRvx/dyV/sB\nJP/kdwS2am91WSIiItfUIqfHM7/+E6NSR/C343uZfMejpI1/Xw1bRESavBZ1pl1tqlm0cz4v71qA\nl6sXy+9+nf/u8YDVZYmIiNyQFtO0q001MVseZMs/PiC4dRfevOdt7mjX2+qyREREbliLadoVlRXk\nfJtFePAoloe/jp+nzeqSRERE6qTFNO1Wbq3IiynAzcXN6lJERETqpUXdiKaGLSIijqxFNW0RERFH\npqYtIiLiINS0RUREHISatoiIiINQ0xYREXEQatoiIiIOQk1bRETEQahpi4iIOAg1bREREQehpi0i\nIuIg1LRFREQchJMxxlhdhIiIiFyfzrRFREQchJq2iIiIg1DTFhERcRBq2iIiIg5CTVtERMRBqGmL\niIg4CFerC2hs8+bNIzc3FycnJ+Lj4+ndu7f9tZSUFNLT03F2diY0NJSEhAQqKytJSEigqKiIqqoq\npk+fTlhYGA899BDl5eV4e3sDEBcXR2hoqFWxaqhrxrS0NJYuXUpwcDAAgwYN4vHHH2ffvn3MnTsX\ngB49evD8889bEecKdc23YsUKsrKyAKiurqa0tJSMjAxGjhxJ+/btcXFxAWDx4sUEBgZakulyteXb\nunUrK1aswN3dnTFjxhAZGXnNZQ4dOsT06dOpqqrC39+fRYsW4e7ublUsu/rkW7hwIZ9//jmVlZU8\n+uijjBo1ihkzZpCfn88tt9wCQGxsLMOHD7ci0hXqmjEnJ4ennnqK2267DYDu3bsze/bsZjOGGzZs\nID093f6evLw8du/e3aT3o/v37+eJJ54gJibG/nN4SVZWFkuWLMHFxYWhQ4cyZcoUoJG2Q9OC5OTk\nmEceecQYY0xBQYGZMGGC/bUzZ86YESNGmAsXLhhjjHn44YfN7t27TWpqqklMTDTGGLN//35z3333\nGWOMiYyMNF999VXjBrgB9cm4ceNG89JLL12xrsjISJObm2uMMeaZZ54xH330USMkqF198l0uLS3N\nrF692hhjzIgRI0xZWVkjVX5jastXVVVlhg4dao4dO2aqqqrMpEmTzKFDh665zIwZM8zmzZuNMca8\n/PLLJiUlpZHTXKk++bKzs83kyZONMcYcP37cDBs2zBhjTFxcnNm2bVujZ7ie+mT87LPPzLRp065Y\nV3MZw+8vP3fuXGNM092Pnj171kRGRppZs2aZt95664rXR48ebb799ltTVVVlJk6caA4cONBo22GL\nmh7Pzs4mPDwcgG7dunHq1CnKysoAcHNzw83NjfLyciorK6moqKBNmzaMGzeOmTNnAmCz2Th58qRl\n9d+I+mS8mvPnz3Pw4EH7EfSIESPIzs5unBC1+CH5Kisreffdd684am5Kast34sQJWrdujc1mw9nZ\nmQEDBpCVlXXNZXJycrj77rsBxxi/a+Xr378/S5cuBaB169ZUVFRQVVVlWYbrqU/Ga2kuY3i55cuX\n88QTTzR63XXh7u7O6tWrCQgIuOK14uJi2rRpQ4cOHXB2dmbYsGFkZ2c32nbYopp2aWkpfn5+9sc2\nm42SkhIAPDw8mDJlCuHh4YwYMYI+ffrQtWtX3Nzc8PDwAGDt2rWMHTvWvvyyZct48MEHmTNnDt99\n913jhrmG+mQE2LFjB7GxsURHR7N37177xndJ27Zt7euxUn3zAWRmZvLjH/8YT09P+3OJiYlMnDiR\nxYsXY5rAhwPWls9ms3H27Fm+/vprLly4QE5ODqWlpddcpqKiwj4N5wjjd618Li4u9unT1NRUhg4d\nar+k8fbbbxMVFcXTTz/N8ePHGz/QVdQnI0BBQQGPPfYYEydO5NNPPwVoNmN4yZ49e+jQoQP+/v72\n55riftTV1bXGfuJyJSUl2Gw2++NL+RtrO2xx17Qvd/lOuqysjFWrVrFlyxZ8fHyIjo5m3759hISE\nABevlebn57Ny5UoAoqKi6NGjB8HBwSQmJpKSkkJsbKwlOWpzIxn79OmDzWZj+PDh7N69m7i4ONas\nWXPN9TQldRnDjRs31rgu/+STTzJkyBDatGnDlClTyMjI4J577mn0DLW5PJ+TkxMvvfQS8fHx+Pr6\nEhQUdN1lanuuKahLvq1bt5Kamsobb7wBwPjx47nlllvo2bMnr7/+OklJScyZM6dR678RN5KxS5cu\nTJ06ldGjR1NcXExUVBSZmZnXXE9TUpcxTE1N5Wc/+5n9saPsR+ujobbDFnWmHRAQUOOo7+jRo/Yj\nvsLCQjp37ozNZsPd3Z2wsDDy8vIA2LBhA9u2beO1117Dzc0NgIiICPuNWyNHjmT//v2NnObq6pOx\nW7du9ht4+vbty/Hjx/Hz86txKeDIkSNXnSpqbPUdw/Lycg4fPlxjJ/LTn/6Utm3b4urqytChQ5vE\nGNaWD+Cuu+7inXfeYdWqVfj6+tKpU6drLuPt7W0/c3GE8YOr5wP4+OOPWblyJatXr8bX1xeAgQMH\n0rNnT8BxtkG4esbAwEDuvfdenJycCA4Opl27dhw5cqRZjSFcnO7v27ev/XFT3Y/W5vv5L41LY22H\nLappDx48mIyMDADy8/MJCAjAx8cHgE6dOlFYWGj/z83Ly6NLly4UFxezbt06kpKS7NPkxhhiYmI4\nffo0cPEH8dJdn1arT8bVq1fz/vvvAxfvmLzU9G699VZ27doFXJxaHjJkiAWJaqpPPoB9+/Zx6623\n2tdz5swZYmNjOX/+PAA7d+5sEmNYWz6AyZMnc+zYMcrLy9m+fTsDBw685jKDBg2yP+8I4wdXz3fm\nzBkWLlzIqlWr7HeKA0ybNo3i4mLAcbZBuHrG9PR0kpOTgYvTr8eOHSMwMLDZjCFcbFitWrWyTxU3\n5f1obYKCgigrK+Obb76hsrKS7du3M3jw4EbbDlvcX/lavHgxu3btwsnJicTERPbu3Yuvry8RERGs\nW7eOtLQ0XFxc6Nu3L9OnT2fJkiV88MEHdOzY0b6O5ORktm7dypo1a/Dy8iIwMJAXX3wRLy8vC5P9\nW10zHj58mOeeew5jDJWVlfZfVSgoKGDOnDlUV1fTp08f+w15VqtrPoCMjAyysrJqTI+vXbuWTZs2\n4eHhwe23387s2bNxcnKyKpZdbfkyMzNZvnw5Tk5OTJo0iXHjxl11mZCQEI4ePUpcXBznzp2jY8eO\nzJ8/3z5TZKW65lu/fj2vvvpqjfsTFixYQFFREYsWLcLLywtvb2/mz59P27ZtLUz2b3XNWFZWxrPP\nPsvp06e5cOECU6dOZdiwYc1mDOHiQfQrr7xS49Lb5s2bm+R+NC8vjwULFnDw4EFcXV0JDAxk5MiR\nBAUFERERwc6dO1m8eDEAo0aNsk/pN8Z22OKatoiIiKNqUdPjIiIijkxNW0RExEGoaYuIiDgINW0R\nEREHoaYtIiLiINS0RUREHISatoiIiINQ0xYREXEQ/w8k9wJLjKx39AAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "peoHmV2M40uU",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 717
+ },
+ "outputId": "e74e3101-65c8-4e63-af14-ec70ecbdb647"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0000006, n_epochs=1000)"
+ ],
+ "execution_count": 47,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.14161786\n",
+ "Loss after epoch 50 is 0.14159875\n",
+ "Loss after epoch 100 is 0.14157961\n",
+ "Loss after epoch 150 is 0.14156051\n",
+ "Loss after epoch 200 is 0.1415414\n",
+ "Loss after epoch 250 is 0.1415223\n",
+ "Loss after epoch 300 is 0.1415032\n",
+ "Loss after epoch 350 is 0.1414841\n",
+ "Loss after epoch 400 is 0.141465\n",
+ "Loss after epoch 450 is 0.1414459\n",
+ "Loss after epoch 500 is 0.1414268\n",
+ "Loss after epoch 550 is 0.1414077\n",
+ "Loss after epoch 600 is 0.14138861\n",
+ "Loss after epoch 650 is 0.1413695\n",
+ "Loss after epoch 700 is 0.14135042\n",
+ "Loss after epoch 750 is 0.14133132\n",
+ "Loss after epoch 800 is 0.14131224\n",
+ "Loss after epoch 850 is 0.14129315\n",
+ "Loss after epoch 900 is 0.14127408\n",
+ "Loss after epoch 950 is 0.14125498\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.111603096\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xl4VOX99/H3TGYSEhJCdpawyRKW\nAEISZJGwBdytWosb4oJb1VqtFhWr2MelYqm/VmsVkbYoqChSa9WCRUFkTwhb2MK+hCU7ZE9m5jx/\nBAYigYSQ5GQmn9d1cSWTc+bM/c0w88lZ5v5aDMMwEBERkUZnNXsAIiIizZVCWERExCQKYREREZMo\nhEVEREyiEBYRETGJQlhERMQktsZ+wKysgsZ+yCpCQgLIyys2dQwNzdtrVH2ezdvrA++vUfVduIiI\noGp/3uz2hG02H7OH0OC8vUbV59m8vT7w/hpVX/1pdiEsIiLSVCiERURETKIQFhERMYlCWERExCQK\nYREREZMohEVEREyiEBYRETFJo0/W0RS99db/sWPHNnJzcygtLaVdu/a0ahXMq6/+sV62f/PN1xEZ\nGYXVevpvnr/+9b2L3u7y5T9w2WVDOXHiOLNmzWDy5OcuepsiItJ4FMLAr371BADffPMf9uzZzaOP\nPl7vjzF9+psEBATU6zY/+WQuAwcmEBYWrgAWEfFACuHzSE1N4ZNP5lBcXMyjjz7Bk08+ytdffwfA\n7343mZtuGk/Pnr149dXfU1BQgNPp5PHHf0u3bt1rtf1rrhlz1vbWr19HUVEhBw7sJyPjEI899iRD\nhgxj4cKvmT9/HhaLhVtvvYOKigq2bk3jqace45lnnuf3v/8ds2Z9SGpqCv/4xwwMw0JERCTPPvsC\nixcvYtOmDeTn53HgwH5uv/1Orr32hgb7vYmISO00uRB+ceXv+M/uL+p1m9d1vYEXh75cp/vu3r2L\njz9egK+vb7XLP/30Yy67bCjXXXcDe/fu4S9/mc6f//y3ixkumZnHmD79TVavXsm///05/ftfyj//\n+T6zZ39MeXkFr7wylddee4P333+X6dPf5PjxfPd9p0//Ax98MBubLZA33pjG//63EIvFwu7du3j3\n3b9z6NBBpk6dohAWEfkJS2Ym9pS14AuMuQYslgZ/zCYXwk1Nt27dzxnAAJs3byI/P49Fi74BoKys\ntNr1nnrqMfc54datQ3j55Wnn3Ga/fpcCEBkZSWFhIfv27aVjx874+bXAz68Fr732RrX3O3HiOBaL\nhbZt25KVVcDAgfFs2JBKjx49iY3th4+PDxERkRQVFdaqdhERr1Vejm3LZuwpa7GtS8aekozPgf3u\nxZa0XRiRkQ0+jCYXwi8OfbnOe60NwW63V/tzh8NxcrmNJ574LbGx/c67nZrOCZ/aHoCPz+nJww3D\nwGr1wTBctRitBcMw3LcqKiqwWKzVblNEpDmxHjmMLSUZe8pa7OuSsW3agKX09E6TKySEsqRxOOIH\n0fLG6xolgKEJhnBTZrFYKD35pKWn7wCgd+9Yli1bSmxsP/bu3cOaNSu59dYJdd5edTp16syBA/sp\nLi7Gx8eHp59+gv/7v7exWKw4nU73eq1atcJisXD48GHs9iA2bEilX79Lq6wjIuL1ysqwbdpQGbYp\nydjXJeOTcci92LBacfSOxRGfQEVcAo6EQTi7dHUffm4ZEQSN1HZXIXwBbrjhZh544C46d76EmJhe\nANx88y288sqLPPzwfbhcLh5//KmL2l51/P39mTTpIR5//GEAbrnldiwWCwMGDOThhyfx3HMvuted\nPPl3PPnkk7hc0L59NGPGjOPbb/9bt4JFRJo6w8CaceiMw8prsW3ehKW83L2KKzycsiuvrgzc+EFU\n9B8AgYEmDvo0i9HIxyazGumvi3OJiAgyfQwNzdtrVH2ezdvrA++v0dT6Skqwbazcyz0VvD5Hj7gX\nGzYbjj593Xu5FfGDcHXqfEEXWTVEfRERQdX+XHvCIiLSNBkG1gP7Tx5WPnkuN20zlooK9yrOyCjK\nrr6OivhBlcHb71Ko5zkZGpJCWEREmobiYuwbUqtcQGXNynQvNux2HH37nQzcQVTEJeCK7tAoHyVq\nKAphERFpfIaBde+e01crpyRj25qG5YwLSZ3t2lN6/Y044hKoiE/A0bc/tGhh4qDrn0JYREQanKWw\nANv61CqHlq05Oe7lhp8fjoHxledxEwbhiEvA1a69iSNuHAphERGpXy4XPrt3VV6tnFwZuD7bt2Jx\nnZ7vwNmxE6WJI92HlR2x/eA8EyN5K4WwiIhcFMuJ49jWpZy+Yjk1BWv+6el0DX9/Ki4bUnlYOS4B\nR3wCrqg2Jo646ahVCKenp/Pwww9z9913M2FC1YkoPv30U+bPn4/VaqVnz55MnToVi4edJD9y5DAT\nJ95KTExPAMrLy7njjrsYMWLUBW/r88/nkZ+fT2LiSJYtW8qkSQ9Wu96pNoTnmpHrTHv27OKNN14/\nq/3hiBGX0bdvf/ftsLAwfv/7P1zwmH9qyZLFjBqVxM6dO85bg4g0Qy4XbNlCi2+XuD+X65O+A8sZ\nn3Z1du5CadIV7okwHL36QC3e65qjGkO4uLiYl156iSFDhpy1rKSkhK+//pq5c+dit9uZOHEi69ev\nZ+DAgQ0y2IbUsWMnd8idOHGce+65g8GDh+DnV7eLALp3j6F795hzLj/VhrA2IXwugYGB9dKX+Kfm\nzJnNqFFJNdYgIt7PkpeLPTXFfcWyLXUdFJzg1KdejYCWVAwbfvLiqUFUDIzHiIgwdcyepMYQ9vX1\nZebMmcycOfOsZf7+/syePRuoDOTCwkIivOCX36pVMGFh4eTk5PCPf8zEZrNz4kQ+/+//vcbrr7/C\n4cMZOBwO7rvvIeLiEkhJWcubb/6J0NAwwsLCadeuPampKSxY8Ckvv/z6edsQ/uUv7/Dll/9i8eKF\nWCxWhg8fyW23TSAz8xjPP/8Mdrudbt161HrsR44c5sEHn2XGjMrnZdKkO3n55Wn8/e/vER4ewY4d\n2zh27CgvvPAyMTE9mTt3NkuXfofFYuWhhx5l+/at7NqVzpQpv+Xmm29x1/Ddd/9j3ry5+Pj4EBPT\ni8cff4pZs2ZU23ZRRDyU04nP9m1nXLG8FtuunVVWcXTrjvWmGymIHUBFXALOnr3ApjObdVXjb85m\ns2Gr4Rf83nvv8cEHHzBx4kQ6dOhwUQNq+eLv8PtP/bYyLLvuBoperH1TiCNHDnPixHEiI6OAyjmZ\nn376ORYu/JqwsHCeffYF8vPz+fWvH2L27E+YMeOvPP/8S3Tv3oOnnnqMdmdc0VdcXHTeNoRZWZks\nXfodf/vbLAB++ctJjBqVxIIF8xgzZhzjx9/GnDn/ZNeu9Iv+PZSXl/PGG3/liy/ms3Dh1wQEBLB0\n6XfMmPFPDh/OYM6cf/LMM88zd+5sXn31j6SmppysoZj33nubf/zjIwICApg8+Qn3sp+2XVQIi3gO\nS3Y29tTT8yvbUtdhPaPLmiswiPLEUZUfD4pPqNzLDQ0jIiKIUi+eEawx1cufLw888AATJ07k/vvv\nJy4ujri4uHOuGxISgM3mc87lBPiCtX7PKQcE+BJwxpRhP50+rKysJQcP7uc3v3kYwzDw8/Nj+vQ/\n0rZtCC1a2Bk8OJ6IiCB27drGunXr2L49DQCHo4LgYD+OHTvK0KGVNQ8bNoSysjJatw7Az8/O8eOZ\ndO/ejejoyiMEs2ZVHlHw8bESHh7Ili3rOHz4EE8++QgA5eWllJbmc/jwQW688XoiIoIYPTqR1NS1\nZ427qKiI3/zmYfftHj16cM8991Sp0WazEhrakhYt7CQmDiUiIohu3TqzZ086R4/uJy5uIFFRwURF\nBTNgwOtAZWOJiIggdw2FhdlcckkXOnWq/KNk+PChHD68j5Yt/Rgy5DIiIoKIielCWVnJOadmq2+N\n9ThmUX2er8nV6HDApk2wejWsWlX5ddeuquv07AlDhrj/WXv1wtfHh+quWW5y9dWzxqrvokI4Pz+f\nnTt3kpCQQIsWLUhMTCQ1NfW8IZyXV3z+jU5+ofJffTv5V1t1c4Lm5hbRoUMn3njjb1XvklVAaWkF\nxcUOsrIKcDjg9tvvYuzYK93rHD9eBljc2ywsLKW8vJz8/GLKyio4fryU0tLysx7T6XSRnV1IcbGD\nyy4byuTJz1VZfuq+WVkF5OYWUl7uOGsbLVu2PGvMR0/OoXpq3dLScnJziygtraCwsHIcx4+XUFJS\nTlFROUVFZWdt1zAMsrIK3DVUfj39+Pn5hfj5+VFUVIbd7k9WVgF5eUXVjrEhaF5ez+bt9UHTqPFU\ng3r353I3rsdSfPr919UqGMeoMe75lR0D4zBah1TdSG7179dNob6G1JhzR1svZqMOh4NnnnmGoqIi\nADZv3kyXLl0uZpNNWu/esSxf/gMAeXm5zJjxNgDh4REcOLAPwzBYv35dlfuc2YawrKyMxx+v3Ns+\n1YYwJqYXqanrKC0txTAM/vzn6ZSVldKxYye2b98K4D70WxsBAS3JycnBMAxycrI5fPjQOdeNienF\n5s0bcTgc5Obm8OyzlR2gXK6qPT06dOjEoUMHKC6ufJ7Xr08lJqZ3rcckIg2svBzb+nX4z3yHoIfu\nJTS+L+Gx3Qi++3YC3vo/7KtX4uzUmZI776bgz2+TuzyZnPT9HJ/3L4onT6FidNLZASyNosY94bS0\nNKZNm0ZGRgY2m41FixYxevRooqOjGTt2LI888ggTJ07EZrMRExPDmDFjGmPcphg9OonU1GQeeuhe\nnE4n9977AAAPPPAwv/vd07Rp09Z9HvmUmtoQvvXWe4wffxuPPHI/VquVxMSR+Pm14Be/uI3nn3+G\nZcuW0LVr91qPsVWrVgwdOpT77ptIt27dz3t1c9u27bjiiqt59NEHMAyDBx+sPCTeo0cM998/kV/+\n8jF3DY888muefPJXWCxW+vW7lP79LyUlZc0F/f5EpH5cSIP6iriEyr3coFYmjljORa0MvZC316j6\nPJu31wf1XGNZGbbNGys/HnS+BvWn5leOT8B5SbcGbWrg7c+hWhmKiDRHpxrUnzqPm5KMbfNGj2lQ\nLxdOISwiYpaSEmybKvdyG6pBvTRtCmERkcZQXYP6zZuwOBzuVZxRbSi75nr3/Mqe1qBeLpxCWESk\nIRQVYd+0AdvJLkL2lLVnN6jvf+npw8pe0KBeLpxCWETkYp1qUH8ybNmwjvBNm5pdg3q5cAphEZEL\nVViIff26czaop5k2qJcLpxAWETkfw6hsUH/yamV7ytqzG9R36FjZoP7kxVMho4aRf7zMxEGLp1AI\ni4icwXLiOLbUM/ZyU1Ow5uW5lxv+/lQMGnx6IozqGtT7+gIKYamZQlhEmi+XC5/0HZWBe6pB/Y7t\nZzeoHz22cn7l+AQcvWPVoF7qjUJYRJqN6hrUWwtOuJerQb00NoWwiHin2jSo79qN8quuqQzc+EFq\nUC+NTv/bRMQr1L5BfXzl+dyTDepFzKQQFhHP43Bg25p2+rDyumRse/dUXaVHDGVxCe5Dy86YnuDj\nY9KARaqnEBaRJq82DerLa2pQL9IEKYRFpGkpL8e2ZbP7amV7SjI+B/a7FxsWC86evSrDNq6ysYGz\new+wWk0ctEjdKIRFxFRqUC/NmUJYRBpPWRms3oL//5ZgW5dS+blckxvUi5hJISwiDeMcDeopL+dU\nC3pXeDhlV1x1ciIMNaiX5kchLCL1o5YN6u3Dh3Gid381qBdBISwidWEYWA8ecIetPWUttrTNWCoq\n3Ks4I6Mou/o693SPpxrUR0QEUZZVYOLgRZoOhbCI1Kw2Der79VeDepELpBAWkap+0qDeti4F25bN\nZzWoL7vuhpPTPapBvUhdKYRFmjlLYQG29annbFBvqEG9SINRCIs0JxfaoD4uAUdsP/DzM3HQIt5L\nISzixdwN6k9dQLUuGWt+vnt5rRrUi0iDUQiLeIszG9SfPKxcbYP6MePUoF6kiVAIi3goS37eycBV\ng3oRT6UQFvEEpxrUrzujdd/O9CqrOLp2o/zqa92dhNSgXqTp0ytUpAmy5ORgX3dqIozzNaivPI+r\nBvUinkkhLGK2nzSoZ8M6wnftqrpKjxjKTs2vHJeAs0eMGtSLeAGFsEgjs2Rmnj6sXE2DeoKDKR85\n+uREGINwxMVjBLc2b8Ai0mAUwiIN6WSD+tNzLNfQoD5+EKFDBnI8p8jEQYtIY1EIi9Qj69EjVeZX\nPmeD+pOBW22Dequ1kUctImZRCIvUVVkZts0b3fMrq0G9iFwohbBIbZyjQb2lvNy9SpUG9XEJVFw6\nUA3qReS8FMIi1SktxbZxQ2WD+pPBW6VBvY8Pjth+OOLiKy+gikvA1bmL9nJF5IIohEUupEF9XAKO\nhEHuBvUiIhdDISzNT3Ex9o3r3RdQ2dYl45N5zL3YsNtx9O1X5YplNagXkYagEBbvdqEN6uMScPRT\ng3oRaRwKYfEuhYXY1687f4P6AXGVgasG9SJiMoWweK4LbVAfP6iyQb2vr4mDFhE5TSEsHuNUg3q2\nbaTVsuXnblB/KnDVoF5EmjiFsDRNLhc+O9OrXLF8ZoN6P9SgXkQ8n0JYmgRLfh621BT3YWVb6jqs\nJ467l5/ZoD5gzAiyu/ZRg3oR8Xi1CuH09HQefvhh7r77biZMmFBl2erVq3njjTewWq106dKFV155\nBavmvpXzqW2D+iuvdl+x7OzV292gPiAiCCOrwIyRi4jUqxpDuLi4mJdeeokhQ4ZUu/yFF17ggw8+\noE2bNjz22GP8+OOPjBgxot4HKp6rVg3qh4+kIiGh8nxuXIIa1ItIs1BjCPv6+jJz5kxmzpxZ7fIF\nCxYQeHJ+3NDQUPLy8up3hOJZHA5s27acnggjZS22vXuqrtIjhrK4hNMN6mN6qkG9iDRLNYawzWbD\nZjv3aqcCODMzkxUrVvDrX//6vNsLCQnAZjP3DTciIsjUx28MjVbjsWOwejWsWlX5NTkZftKgniuu\ngMGDYcgQGDQIW0jIRV+M4O3PoerzfN5eo+qrH/VyYVZOTg4PPfQQU6dOJSQk5Lzr5uUVn3d5Q4uI\nCCLLy88nNliNJxvUn7pa2Z6Sgs+Bfe7FhsWCM6bnyauVB1ERPwhnt+5V++M6gIscm7c/h6rP83l7\njaqvbtuszkWHcGFhIffffz+PP/44l19++cVuTpqQWjeoPzXdY3UN6kVE5JwuOoRfe+017rrrLhIT\nE+tjPGKWWjSod/bqc/Jq5XgcCYPUoF5E5CLVGMJpaWlMmzaNjIwMbDYbixYtYvTo0URHR3P55Zfz\nxRdfsH//fubPnw/Atddeyy233NLgA5eLoAb1IiJNQo0hHBsby4cffnjO5WlpafU6IGkAJSWVDerP\n+FyuGtSLiJhPM2Z5G8OAffvwW/S9u4uQbfMmLA6HexU1qBcRaRoUwp7uJw3q7SlrISuTU5dHGXY7\njn791aBeRKQJUgh7EsPAum/vyY8HnbtBPTffTGHfgWpQLyLSxCmEm7LCQuwbUk93ElqXjDU7273Y\n8PPDMTCeirgEKuIrZ6BytWtPREQQJV78GT4REW+hEG4qftqgfl0yPtu2nN2g/safn+6X26cv+PmZ\nOGgREbkYCmGTnGpQ7/6YkBrUi4g0OwrhxlBDg3oAZ8fOlI4eS0VC5ZSPalAvIuL9FMINwN2g/lQn\noeoa1A+93D3dY8XAeIzISBNHLCIiZlAIX6yLbFAvIiLNl5LgAtWqQX3iKCri4yv3dAfGq0G9iIhU\nSyF8PhfaoD5+EM4eMWpQLyIitaIQPoMlM7PKYWX7hlQsZzSod7UKpnzUmJOfyx2EIy4eI7i1iSMW\nERFP1nxDuDYN6nv2qpx16mToOrv3qNqgXkRE5CI0mxA+1aCebRtpvWz5uRvUn9rLHTAQo1WwiSMW\nERFv550hfKpB/bpkbCnJZzWot6lBvYiINAGeH8IX2KA+cMwIsjv3VIN6ERExnUeHsM/OdIJv+zk+\nB/a7f1ZTg/rAiCBQcwMREWkCPDqEcbkwglqpQb2IiHgkjw5hZ0xP8pasMHsYIiIidaLP24iIiJhE\nISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKF\nsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTC\nIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiapVQinp6eTlJTEnDlzzlpWVlbG008/zU033VTv\ngxMREfFmNYZwcXExL730EkOGDKl2+euvv06vXr3qfWAiIiLersYQ9vX1ZebMmURGRla7/IknniAp\nKaneByYiIuLtagxhm81GixYtzrk8MDCwXgckIiLSXNga+wFDQgKw2Xwa+2GriIgIMvXxG4O316j6\nPJu31wfeX6Pqqx+NHsJ5ecWN/ZBVREQEkZVVYOoYGpq316j6PJu31wfeX6Pqq9s2q6OPKImIiJik\nxj3htLQ0pk2bRkZGBjabjUWLFjF69Giio6MZO3Ysjz32GEePHmXv3r3ceeedjB8/nuuuu64xxi4i\nIuLRagzh2NhYPvzww3Muf/PNN+t1QCIiIs2FDkeLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iI\nmEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJi\nEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJ\nFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZR\nCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQh\nLCIiYhKFsIiIiEkUwiIiIiapVQinp6eTlJTEnDlzzlq2cuVKbr75Zm655Rbefvvteh+giIiIt6ox\nhIuLi3nppZcYMmRItctffvll3nrrLT7++GNWrFjBrl276n2QIiIi3qjGEPb19WXmzJlERkaetezg\nwYMEBwfTtm1brFYrI0aMYNWqVQ0yUBERkYZmGAYOl6PRHs9W4wo2GzZb9atlZWURGhrqvh0aGsrB\ngwfrb3QiIiIN6FjRUdZnprIhc93Jr6k4cZJ8xyZCWoTWvIGLVGMI17eQkABsNp/GftgqIiKCTH38\nxuDtNao+z+bt9YH31+iJ9ZU5ylh9aDUrDq4g+XAyyRnJZBRkVFnnkpBLSOqSRJd27bD72Bt8TBcV\nwpGRkWRnZ7tvHzt2rNrD1mfKyyu+mIe8aBERQWRlFZg6hobm7TWqPs/m7fWB99foKfW5DBdbc7aw\n7NBSlh1awurDKyl2nM6gqIA2XNn5ai6NHHjy3wBCW4SdUV9pvY3lXH+0XFQIR0dHU1hYyKFDh2jT\npg1Llixh+vTpF7NJERGROnG4HBwo2M+qjBUsO7SEHzN+ILvk9I5iz9BeJEaPZEi7yxkYGUfbwHYm\njrZSjSGclpbGtGnTyMjIwGazsWjRIkaPHk10dDRjx47lxRdf5MknnwTg6quvpkuXLg0+aBERaZ5K\nHaXsP7GPfSf2su/4HvYe38O+E3vZe3wPBwsOVLmoqk3LttwSczuJ0SNJjB5JVMs2Jo68ejWGcGxs\nLB9++OE5lyckJDBv3rx6HZSIiMiZUo6u5d2Nb/P1ni9xGs6zlof7h9M/YgCdW3Uhvk0CidGj6Na6\nOxaLxYTR1l6jX5glIiJSG06Xk//u/Zp3Nr5F8tE1APQK7UNcVDydgy+hS3AXOrfqQufgLgT5tjJ5\ntHWjEBYRkSalsKKQedvnMmPj39h3Yi8AYztdwS8v/RXD2g1v8nu3F0IhLCIipiuuKGZn3g7+s/vf\nfLD17+SX5ePn48edve/mwX6P0CM0xuwhNgiFsIiINJrCikJ25u5gR9520vN2sCN3GzvydnDwxH4M\nDADCWoTxVPwz3BN7PxEBESaPuGEphEVEpEE4XA625Wwh+dhaUo5W/jt1ePlMEf6RDGs/nB4hMQyI\njOP6bjfib/M3YcSNTyEsIiL1Iq80tzJsj60l+ehaUo+to9hR5F7e2q81w9uPICa0Jz1CetIztBc9\nQmMIbRFm4qjNpRAWEZE6O3BiP9/s/Q9f7/kPa4+sdh9SBogJ6UlCm8uIbzOI+KhBdAvpjtWiNvZn\nUgiLiEitGYbBlswtfLjuY77Z8xWbszcCYMFCQpvLGB49goQ2gxgYGU/rFiEmj7bpUwiLiEiNtudu\n47Mdn/D1ni/Zc3w3AHarndEdk7jmkuu5ovPVRAacv3eAnE0hLCIi1Sp1lPLVnn8ze8vfWXOksld8\ngK0lN/e+maT2V5HUcRyt/IJNHqVnUwiLiEgVe/J38cHWf/LJ9jnkluYCMKrDGCb0vpukTuPo2DbS\nI7ooeQKFsIiIFyuuKGZ77la25WzFYTgIsAUQYG95+qs9gJYnv08+upbZW/7OskNLgMr5mH814Akm\n9L6LLsGXmFyJd1IIi4h4ieySbNKyN5GWvZm07I2kZW9mV/5OXIbrgrYztN3l3NXnXq6+5Dr8fPwa\naLQCCmEREY9lGAYbMlP5NL3ySuUjRYerLA+0BzGozWBiw/vSJ6wv/nZ/iiuKKaoopLiimGJHMcUV\nRe6vUS3bMqHXXV47RWRTpBAWEfEwhwoO8nn6p3y642N25qcDlVM9XtH5KvqE9yU2rB+x4X3p2KqT\nPpfbxCmERUQ8QGF5AV/t+ZLPdnzC8oxlGBj4+fhxQ7ebGB9zGyM7jMFm1Vu6p9EzJiLShG3O2sj7\nm2fwxa7PKXGUADC47VDGx9zGdV1/RrBfa5NHKBdDISwi0sRUOCv4796vmLn5Xffnczu16sytPe/g\n5h630KlVZ3MHKPVGISwi0kRkl2QzZ+s/+WfaLA4XZQAwumMS9/d9iFEdk3R+1wsphEVETOBwOcgp\nzSG7OItjxUf5964FLNj5GWXOMlraA5nU9wEmxT5It5DuZg9VGpBCWESkgRwtOsLqwytJPrqGI0VH\nyCnNJrs4i+ySLPLK8s5av0srkLt4AAAcCklEQVTwJdzX90Fu7XkHQb6tTBixNDaFsIhIPTAMgwMF\n+1l1eAUbViazZO9S9h7fU2UdCxZCW4QSGRBF77BYwvzDCfcPJ8w/nLioeEZ2GKNDzs2MQlhE5ByO\nFh3ho20fsiN3GxaLFavFio/FB+vJ760WKxasnCjPZ+2RNe7zuACtfIMZ1+lKBrcbxmVtB9O51SWE\ntgjFx+pjYkXS1CiERUTOYBgGP2b8wD/TZvHfvV/hNJy1ul+4fwTXdb2BIW2HcnWfcURZOilwpUYK\nYRERIK80l0+2f8QHW//O7vxdAPQJ68vdsZNI6jgOq8WKy3DhwoXLcOE0nBiGC5dh4OvjS8egTlgs\nFgAiIoLUZUhqRSEsIs2WYRikZqbwz7RZ/HvXAkqdpfj5+DE+5jbu7jOJuKgEd7CKNASFsIg0O5nF\nmcxPn8fH2z5kR952oPLK5Lv6TOLWnrcT2iLM5BFKc6EQFpFmocJZwXcH/sdH2z9k8f5FOFwOfK2+\n/KzrTdzReyKJ0SN1ZbI0OoWwiHg0l+HC6XLiNE7+czlOfl953jbr5F7vpzs+JrskC4C+4f25vdcE\nbur+C0JahJpcgTRnCmER8Uh7ju/m+eXP8L/9i2q1fohfCPf3fYhbe02gb3i/Bh6dSO0ohEXEoxRX\nFPOX1Om8vf5Nyl3l9AnrS6h/GDaLDz4WH3ysPlgtPtisNnwsVvx8WjC20xVc0eVq/Hz8zB6+SBUK\nYRExzYmy4wTYW9aqD65hGHy150umrpjCocKDtGvZnv837FWu63qDrmAWj6UQFpFGtzl7E39eN52v\ndv+bQN8gBrcdwtB2wxnW/nL6hvc/a5KLnXnpTPnxt/xwaAl2q51fD3ySx+OeoqW9pUkViNQPhbCI\nNJrUYym8vfj/+E/6fwDoHRZLqaOE/+1f5D63G+TbiiFthzK0/XAuazuYr/f8hxkb36bCVcGoDmN4\ndfjrdG2tzkLiHRTCItLgVh9ZxRsp01h68HsAEtpcxpPxkxnVIQmLxcKRwsOsPLyclYeXsyLjR77d\nv5Bv9y90379DUEdeGvYaV3W5RoeexasohEWkQbgMF8szlvFGyuusPLwcgOHtR/D7MVPp0zKuSpi2\nDWzHz3uM5+c9xgO4Q3n1kVVEB0Zzf79fEmAPMKUOkYakEBaRi1bmLGNH7jY2Z20iLWcTm7M2sSUn\njaKKQgDGdBzLE3GTGdT2slrNq/zTUBbxVgphETmv4opicktzyCvNJbc0l9zSHHJLc8krzWX/iX1s\nzt5Eet52HC6H+z4+Fh+6h/Tg0siB3Bt7P5dGDjSxApGmSyEsIm4nyo6zPONHfjj0PT8e+oFDBQcp\ndZae9z4BtgAujRhIbHhf+kb0JzasLz3DeuNv82+kUYt4LoWwSDPmcDnYkJnK0oPfs/Tg96w7luzu\nnxtoD6JnaC9C/cMI8QslzD+MkBahhLQIJaxF5fftWranS/Al6psrUkcKYZFmxOFysDUnjdWHV7Ly\n8AqWZyzjRPlxAKwWKwMi4xjZYTQjO4xhYGQcdh+7ySMW8W4KYREvVuIoIfVYCmuOrGL1kZWkHE2m\nsOL0RVEdgzrxs243MbLDaIa3T6R1ixATRyvS/CiERbxImbOM5KNr+OHgEpZnLGNT1gYqXBXu5d1a\nd2dw25sY1HYwg9sOpVOrzvrcrYiJFMIiHswwDLbmbOGHQ0tYdmgJqw+vpNhRDFReodw3vB+XtRvK\n4LZDGdRmMBEBESaPWETOVKsQfvXVV9m4cSMWi4UpU6bQr9/pNmCLFy/mnXfewdfXl2uuuYYJEyY0\n2GBFpPIjQwv3fc3/9i1i2aGlZJVkupfFhPRkRIdRJEaPZGi7ywn0DTJxpCJSkxpDeO3atezfv595\n8+axe/dupkyZwrx58wBwuVy89NJL/Otf/6J169bcf//9JCUl0aZNmwYfuEhz4nQ5WXH4Rz7b8Qlf\n7fnSPQlGhH8kN/e4hcTokYyIHkXbwHYmj1RELkSNIbxq1SqSkpIA6Nq1K8ePH6ewsJDAwEDy8vJo\n1aoVoaGhAAwePJiVK1dy0003NeyoRZqJbTlb+Sz9Ez5P/5QjRYeBynmUH+j3ENd3vYneYX10TlfE\ng9UYwtnZ2fTp08d9OzQ0lKysLAIDAwkNDaWoqIh9+/bRvn171qxZw6BBgxp0wCLeyuFycKBgP8n5\nh1m1J5kvdi0gLXsTAK18g7mz9938osetDGo7GKvFavJoRaQ+XPCFWYZhuL+3WCy89tprTJkyhaCg\nIKKjo2u8f0hIADabuR/sj4jw/vNk3l6jJ9dXUFbAxmMb2ZG9g/ScdHbkVH7dlburypXMNquN62Ou\n585+d3Jtj2tpYWth4qjrlyc/f7Xl7TWqvvpRYwhHRkaSnZ3tvp2ZmUlExOkrLAcNGsRHH30EwJ/+\n9Cfat29/3u3l5RXXdaz1ojaTx3s6b6/Rk+orc5axNTuN9VmprD+2jg2ZqaTn7cDAqLJesF9r+kX0\n55LgbvRvH0tb344MbTecMP8wAAryKiigorqH8Die9PzVlbfXqPrqts3q1BjCw4YN46233uLWW29l\ny5YtREZGEhgY6F5+3333MW3aNPz9/VmyZAn33HNP/Y1axIOUOEpIz93Olpw0NmVtYH3mOrZkp1Hu\nKnev09IeyJB2w+gfMYAeITF0DelOt9bdCWsR5j636+1vcCJyWo0hPHDgQPr06cOtt96KxWJh6tSp\nLFiwgKCgIMaOHcv48eO59957sVgsPPDAA+6LtES8lWEYHC06wpaczWzN2cKW7M1syUljV/5OXIbL\nvZ7daic2vC+XRg5kQGQcAyLj6Na6u+ZZFhG3Wp0Tfuqpp6rc7tmzp/v7cePGMW7cuPodlUgTtTFz\nPb9cfB+78ndW+XmQbysS2lxGn7BY+oT3JTasL73DY/Hz8TNppCLiCTRjlkgtGIbBB1v/wXM/Tqbc\nVc6Vna+mb0R/+oT1pU94LB2DOumjQiJywRTCIjUoqijitz88zvz0eYT4hTA76SPGdNLRHxG5eAph\naVaKKorILsmq9Z5reu4OJi26kx1524mLimfmuNlEB3VohJGKSHOgEBavZhgG23K38v2BxSw5+B1r\nDq+k3FVOx1aduarz1VzV5VoGtR2MzXr2S2HBzs/4zZLHKHYUcX/fh5g69GV8fXxNqEJEvJVCWLxO\nXmkuPxxcwpKD37Hk4HccLTriXtY3vD/RQR348dAPzNj0N2Zs+hshfiGM7XwlV3a+hlEdx2Cz2nhh\nxbP8I+19WtoDeX/cbK7vdqOJFYmIt1IIi1fYlbeT/+77moV7v2bdsWT3R4XCWoRxU/dfMLpjEiM7\njCEyIBKonERjRcaPLNz7NQv3fcOnOz7m0x0f4+fjR1RAGw4U7KdXaG9mXfEh3UK6m1maiHgxhbB4\nJJfhIvVYCv/dWxm8O/PTAbBarMRHDWJMx7GM6jiGfhGXVjvPsp+PH6M7JjG6YxKvJf6JjZnrWbjv\naxbu/Ybtudu4JeZ2piW+QYA9oLFLE5FmRCEsHqPCWcGPGUv5fvUivtj+bzKLjwHgb/Pnqi7XclWX\naxjb6Ur3VI+1ZbVYGRAVx4CoOJ697AXKnGX6fK+INAqFsDRphmGQfHQtn++cx5e7/kVOaQ5QeZj5\ntp4TuKrLtSRGj6zXPVYFsIg0FoWwNEnbc7exIP0zFuz8jAMF+wEI94/gvr4PMjHuDrq36KvpH0XE\n4ymEpUk41W3ox4xl/GvnfLbkbAYqGx6Mj7mNn3cfz/DoEdisNjU4EBGvoRCWRud0OdmZn876Y+tY\nn1nZ3m9LTpq7l67daufKzlfz8x7jGdvpSl0cJSJeSyEsDa64opjko2tYnrGMtUdXsylrI0UVhe7l\nvlZfYsP7MiAyjoFR8YztdAUhLdSNS0S8n0JY6l25s5zUzHUsP/QDyzOWkXJ0rbunrgULPUJiGBAV\nV9niL2Kgug2JSLOlEJaL5nA52Jy1kR8zlrEiYxlrjqyi2FEMVIZu34j+DGs3nOHRiVzWdghBvq1M\nHrGISNOgEJYL5jJcbM3ZwvKMH1iR8SMrD6+goPyEe3lMSE8uj07k8vYjGNpumA4ti4icg0JYADhW\ndJTN2RupcDlwuBy4DCcO9/cuHIaDoopC1h5Zw8rDP5Jbmuu+b5fgS7ih200Maz+cYe0TiQqIMrES\nERHPoRBuppwuJ+uOpfDdgUUs3v8/NmdvrPV9owM7MDbmSi5vn8jl7RNpHxTdgCMVEfFeCuFmJLsk\nm+8P/I/v9n/L0oPfk1eWB1R+JCgxehRD2g0lwNYSm9UHH6sNm8WGzWrDarFis9rwtfrSN6I/nVt1\nqVUvXhEROT+FsJc7UXacL3d/wbwdH7H2yGoMDADatWzPtV1vIKnTOIZHjyDQHmjySEVEmh+FsBdy\nupwsOfAd83bM5Zs9X1HqLMWChcvaDmFs5ytJ6jiOnqG9tDcrImIyhbAXSc/dwbwdH7Fg16dkFGQA\ncElwV26JuZ1fxNxKdFAHk0coIiJnUgh7sApnBeuOJbP04Hd8d2AxG7PWAxDsF8ydve/hlpjbSWgz\nSHu8IiJNlELYgxiGwe78Xfxw6HuWHvye5Rk/uqd/9LH4MLpjErfG3MGEhFsozHeYPFoREamJQriJ\nc7gcLDu0lK92/5ulB7/nUOFB97KurbsxInoUIzuMYVj7y90zUfnb/SlEXYZERJo6hXATdKqR/YKd\nn/Ll7n+RXZINQGu/1lzf9UZGdBjFiOhRdGzVyeSRiojIxVAIN6BSRymrj6xk2aGlVDjLaR8UTfvA\nDkQHRtM+qAPh/uFYLVb3+ttytrJg52f8a+f8MxrZh3Nv7P3c2P0XxEclqJG9iIgXUQjXo1PnbJcc\nXMz3Bxaz8vByShwl51zf1+pLu8D2RAd1IKckm225W4HTjexv6n4zw9uPxO5jb6wSRESkESmEL5LD\n5WDx/m9ZvP9blh78zr0HC5WNDEZ2HMOoDmMIbRHKoYJDZBQe5FDhITJOfp9RmMHyjGX4Wn25qsu1\n/Lz7L0jqdIUa2YuINAMK4To6UXacOds+4P1N77ovlmrlG8x1XW9gVIfK4P3pnMqXRg6sdltlzjKc\nLqeCV0SkmVEIX6BDBQd5b9M7zNk6m8KKAgJsAdwbez83dR/PwKg4bNYL/5X6+fiBTvWKiDQ7CuFa\nWn9sHe9sfIv/7P43TsNJVEAbfj3wN0zsc4/65YqISJ0ohM+j3FnOwr1f8/7mGaw+shKA3mGx/LL/\no9zY/WZ8fXxNHqGIiHgyhXA1DpzYz5yts5m77QOySjIBGNNxLA/1f5TE6JGaBlJEROqFQvikU1c5\nz94yi+8PLMbAINivNQ/2e5iJfe6le0gPs4coIiJexqtDOLskm3c3/JX8snxa2lvS0t6SqJAwjDLb\nyduBBNgDSDm6ljlbZ3O4qLLzUFxUAnf1uZefdbsJf5u/yVWIiIi38soQdrqczN76d/6w5iWOl+XX\n6j4t7YHc3WcSE/vcS2x43wYeoYiIiBeGcPLRNTyz7Ck2Z28kyLcVr1w+jZEdxlBUUUhRRRG2ABeH\ns7Moqihy/ywqoA0/63Yjgb5BZg9fRESaEa8J4aziLF5ePZWPt88B4JaY23l+yP8jMiCyynoREUFk\nhajDkIiImM/jQ9jpcvLPLbN4be3LHC/Lp09YX15L/BOXtR1s9tBERETOy6NDOLM4k9u++jmbszfS\nyjeYVy9/nbtj76vTrFUiIiKNzaPTau/xPWzL3XLOQ88iIiJNmUeH8GVtB3PggUzt+YqIiEey1rxK\n06YAFhERT1WrBHv11VfZuHEjFouFKVOm0K9fP/eyuXPn8uWXX2K1WomNjeW5555rsMGKiIh4kxr3\nhNeuXcv+/fuZN28er7zyCq+88op7WWFhIbNmzWLu3Ll8/PHH7N69mw0bNjTogEVERLxFjSG8atUq\nkpKSAOjatSvHjx+nsLAQALvdjt1up7i4GIfDQUlJCcHBwQ07YhERES9R4+Ho7Oxs+vTp474dGhpK\nVlYWgYGB+Pn58cgjj5CUlISfnx/XXHMNXbp0Oe/2QkICsNnM7WAfEeH9M2N5e42qz7N5e33g/TWq\nvvpxwVc1GYbh/r6wsJAZM2awcOFCAgMDueuuu9i+fTs9e/Y85/3z8orrNtJ6EhERRFaWd8+Y5e01\nqj7P5u31gffXqPrqts3q1Hg4OjIykuzsbPftzMxMIiIiANi9ezcdOnQgNDQUX19f4uPjSUtLq6ch\ni4iIeLcaQ3jYsGEsWrQIgC1bthAZGUlgYCAA7du3Z/fu3ZSWlgKQlpZG586dG260IiIiXqTGw9ED\nBw6kT58+3HrrrVgsFqZOncqCBQsICgpi7NixTJo0iYkTJ+Lj48OAAQOIj49vjHGLiIh4PItx5kne\nRmD2eQRvP5cB3l+j6vNs3l4feH+Nqq9u26yOx8+YJSIi4qkUwiIiIiZp9MPRIiIiUkl7wiIiIiZR\nCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiY5IK7KDVFr776Khs3bsRisTBlyhT69evnXjZ3\n7ly+/PJLrFYrsbGxPPfcczgcDp577jkOHDiA0+lk8uTJxMfHc+edd1JcXExAQAAATz/9NLGxsWaV\n5Xah9S1YsIC//OUvdOzYEYChQ4fyy1/+ku3bt/Piiy8CEBMTw+9//3szyqnWhdb4zjvvsHLlSgBc\nLhfZ2dksWrSI0aNH06ZNG3x8KttlTp8+naioKFNqOtP56lu8eDHvvPMOvr6+XHPNNUyYMOGc9zly\n5AiTJ0/G6XQSERHBH//4R3x9fc0qy60u9b3++uusW7cOh8PBgw8+yLhx43jmmWfYsmULrVu3BmDS\npEmMHDnSjJKquND61qxZw69//Wu6d+8OQI8ePXj++eeb7PMHF17jZ599xpdffuleJy0tjfXr1zfZ\n99H09HQefvhh7r77bvf/wVNWrlzJG2+8gY+PD4mJiTzyyCNAI70GDQ+3Zs0a44EHHjAMwzB27dpl\njB8/3r2soKDAGDVqlFFRUWEYhmHcc889xvr164358+cbU6dONQzDMNLT042f//znhmEYxoQJE4wd\nO3Y0bgE1qEt9n3/+ufHaa6+dta0JEyYYGzduNAzDMH7zm98YS5cubYQKalaXGs+0YMECY+bMmYZh\nGMaoUaOMwsLCRhp57ZyvPqfTaSQmJho5OTmG0+k07r33XuPIkSPnvM8zzzxjfPPNN4ZhGMaf/vQn\nY+7cuY1czdnqUt+qVauM++67zzAMw8jNzTVGjBhhGIZhPP3008b333/f6DWcT13qW716tfGrX/3q\nrG01xefPMOpW40/v/+KLLxqG0TTfR4uKiowJEyYYv/vd74wPP/zwrOVXXXWVcfjwYcPpdBq33Xab\nsXPnzkZ7DXr84ehVq1aRlJQEQNeuXTl+/DiFhYUA2O127HY7xcXFOBwOSkpKCA4O5vrrr+fZZ58F\nIDQ0lPz8fNPGX5O61Fed8vJyMjIy3H/djho1ilWrVjVOETW4mBodDgcff/zxWX/ZNiXnqy8vL49W\nrVoRGhqK1Wpl8ODBrFy58pz3WbNmDWPGjAGaznNYl/oSEhL4y1/+AkCrVq0oKSnB6XSaVsP51KW+\nc2mKzx9cfI1vv/02Dz/8cKOPu7Z8fX2ZOXMmkZGRZy07ePAgwcHBtG3bFqvVyogRI1i1alWjvQY9\nPoSzs7MJCQlx3w4NDSUrKwsAPz8/HnnkEZKSkhg1ahT9+/enS5cu2O12/Pz8AJg9ezbXXnut+/5v\nvvkmd9xxBy+88IK7RaOZ6lIfwNq1a5k0aRJ33XUXW7dudb+QTgkLC3Nvx2x1rRHg22+/5fLLL6dF\nixbun02dOpXbbruN6dOnYzSBCeHOV19oaChFRUXs27ePiooK1qxZQ3Z29jnvU1JS4j701VSew7rU\n5+Pj4z5cOX/+fBITE92nEObMmcPEiRN54oknyM3NbfyCfqIu9QHs2rWLhx56iNtuu40VK1YANMnn\nD+peI8CmTZto27atu888NL33UZvNVuU94kxZWVmEhoa6b5+qvbFeg15xTvhMZ77pFhYWMmPGDBYu\nXEhgYCB33XUX27dvp2fPnkDlucYtW7bw7rvvAjBx4kRiYmLo2LEjU6dOZe7cuUyaNMmUOs6lNvX1\n79+f0NBQRo4cyfr163n66ad5//33z7mdpuZCnsPPP/+8yrntxx57jOHDhxMcHMwjjzzCokWLuPLK\nKxu9hvM5sz6LxcJrr73GlClTCAoKIjo6usb7nO9nTcGF1Ld48WLmz5/P3//+dwB+9rOf0bp1a3r1\n6sV7773HX//6V1544YVGHX9NalNf586defTRR7nqqqs4ePAgEydO5Ntvvz3ndpqaC3kO58+fz403\n3ui+7Qnvo3XRUK9Bj98TjoyMrPJXWWZmpvsvst27d9OhQwdCQ0Px9fUlPj6etLQ0AD777DO+//57\n/va3v2G32wEYO3as+2Km0aNHk56e3sjVnK0u9XXt2tV9McuAAQPIzc0lJCSkymH3Y8eOVXtoxgx1\nfQ6Li4s5evRolTeFG264gbCwMGw2G4mJiU3+OQQYNGgQH330ETNmzCAoKIj27duf8z4BAQHuPYum\n8hzWpT6AH3/8kXfffZeZM2cSFFTZ5m3IkCH06tUL8IzXIFRfX1RUFFdffTUWi4WOHTsSHh7OsWPH\nmuTzB3V/DqHyEPuAAQPct5vi++j5/LT2U89LY70GPT6Ehw0bxqJFiwDYsmULkZGRBAYGAtC+fXt2\n797t/oWlpaXRuXNnDh48yCeffMJf//pX92FpwzC4++67OXHiBFD5H+vUlY1mqkt9M2fO5KuvvgIq\nrwg8FWCXXHIJKSkpQOVh3OHDh5tQ0dnqUiPA9u3bueSSS9zbKSgoYNKkSZSXlwOQnJzc5J9DgPvu\nu4+cnByKi4tZsmQJQ4YMOed9hg4d6v55U3kO61JfQUEBr7/+OjNmzHBfCQ3wq1/9ioMHDwKe8RqE\n6uv78ssvmTVrFlB5uDMnJ4eoqKgm+fxB3WqEyhBq2bKl+/BsU30fPZ/o6GgKCws5dOgQDoeDJUuW\nMGzYsEZ7DXpFF6Xp06eTkpKCxWJh6tSpbN26laCgIMaOHcsnn3zCggUL8PHxYcCAAUyePJk33niD\nr7/+mnbt2rm3MWvWLBYvXsz777+Pv78/UVFRvPLKK/j7+5tYWaULre/o0aP89re/xTAMHA6H+9L6\nXbt28cILL+Byuejfv7/74rSm4EJrBFi0aBErV66scjh69uzZfPHFF/j5+dG7d2+ef/55LBaLWWW5\nna++b7/9lrfffhuLxcK9997L9ddfX+19evbsSWZmJk8//TRlZWW0a9eOP/zhD+4jOWa60PrmzZvH\nW2+9VeX8/rRp0zhw4AB//OMf8ff3JyAggD/84Q+EhYWZWFmlC62vsLCQp556ihMnTlBRUcGjjz7K\niBEjmuzzB3X7P5qWlsaf//znKqe7vvnmmyb3PpqWlsa0adPIyMjAZrMRFRXF6NGjiY6OZuzYsSQn\nJzN9+nQAxo0b5z583hivQa8IYREREU/k8YejRUREPJVCWERExCQKYREREZMohEVEREyiEBYRETGJ\nQlhERMQkCmERERGTKIRFRERM8v8By+QHC8TsRmIAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "KjY_KnlE5ClG",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Drive the loss to a minimum."
+ ]
+ },
+ {
+ "metadata": {
+ "id": "JKiHjGN15HPX",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# YOUR CODE HERE\n",
+ "with tf.Session() as sess:\n",
+ " \n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " prev_loss = None\n",
+ " \n",
+ " while True:\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " if prev_loss == None:\n",
+ " prev_loss = curr_loss\n",
+ " else:\n",
+ " if prev_loss == curr_loss:\n",
+ " break\n",
+ " final_loss = curr_loss\n",
+ " print('Minimum Loss = '+str(final_loss))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ }
+ ]
+}
\ No newline at end of file