Bayes algorithm introduction

Bayes theorem works using conditional probability. My "Introduction to the Statistics textbook describes this in the first chapter as the probability(P) of an event (B) occurring given evidence (A) or written as P(B|A). Bayes theorem is the probability of an event B occurring when we already know that event A has occurred.

Bayes theorem is applied by measuring probability for virus detection, cancer, and defects for many problems. I use Bayesian interpretation to measure the degree of belief and frequentist interpretation to measure the proportion of outcomes given A.

Bayes algorithm

I start by first understanding the algorithm and breaking it up using a spreadsheet. This spreadsheet will help me understand the algorithm and help me code it. It will also help me write the tests for evaluating probability.

(P(n1┤|n3)×P(n3))/(P(n1┤|n3)×P(n3)+P(n1│common)×(1-P(n3))) ×P(n1┤|n3)

P(B|A) * Bayes Factor = posterior odds or posterior probability

code example

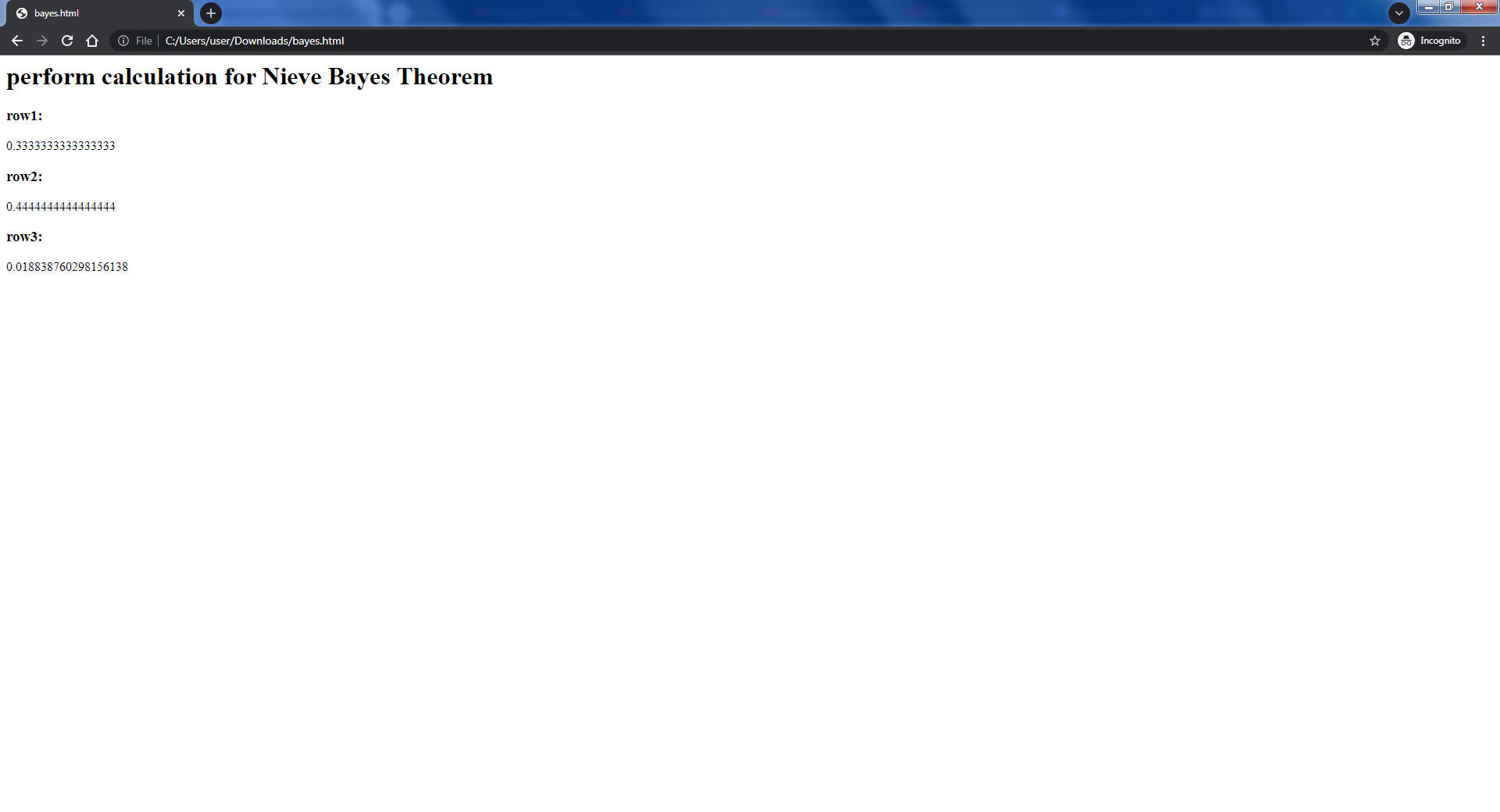
Below is an example of using the Bayes Algorithm. The data will come from a list you will want to iterate over in the application. You may want to use one array of data and search for a pattern (B|A). You need to search for occurrences of B, but not include (B|A), which is how we get the B_in_common and why we subtract the A_num from the total_size to compute the common_num.

function mr_bayes(total_size, B_num, A_num, B_in_common)
{
  const p_B_A = B_num/A_num;
  const p_A = A_num/total_size;
  const numerator = p_B_A * p_A;
  const common_num =  total_size - A_num;
  const p_B_common = B_in_common/common_num;
  const p_common = 1-p_A;
  const denominator = numerator+(p_B_common * p_common);
  const bayes_factor = numerator/denominator;
  const pp = p_B_A * bayes_factor;
  return pp;
}

Viewing the HTML file.