Mathematician's Life

1. Adaptive Base Representation Theorem: An Alternative to Binary Number System,
   DOI Number: 10.1007/978-981-96-7499-2_37

   Abstract: This paper introduces the Adaptive Base Representation (ABR) Theorem and proposes a novel number system that offers a structured alternative to the binary number system for digital computers. The ABR number system enables each decimal number to be represented uniquely and using the same number of bits, n, as the binary encoding. Theoretical foundations and mathematical formulations demonstrate that ABR can encode the same integer range as binary, validating its potential as a viable alternative. Additionally, the ABR number system is compatible with existing data compression algorithms like Huffman coding and arithmetic coding, as well as error detection and correction mechanisms such as Hamming codes. We further explore practical applications, including digital steganography, to illustrate the utility of ABR in information theory and digital encoding, suggesting that the ABR number system could inspire new approaches in digital data representation and computational design.
   
   Adaptive Base Representation Theorem:
   For a given positive integer n, the set of numbers representable with n bits in the Binary Number System is identical to the set of numbers representable with n bits in the Adaptive Base Representation Number System.

   Formally,

   Let Bn denote the set of numbers representable using n bits in the Binary Number System, and An denote the set of numbers representable using n bits in the Adaptive Base Representation Number System, where n is a positive integer. Then,
   Bn = An, ∀n ≥ 1
   
   
   Cite as: Kumar, R. (2026). Adaptive Base Representation Theorem: An Alternative to Binary Number System. In: Senjyu, T., So-In, C., Joshi, A. (eds) Smart Trends in Computing and Communications. SmartCom 2025. Lecture Notes in Networks and Systems, vol 1458. Springer, Singapore. https://doi.org/10.1007/978-981-96-7499-2_37
   

   Resources:
   

   1. Published paper: click here
   2. Published paper (DOI Link): click here
   3. Paper on archive.org: click here
   4. Preprint on github.com: click here
   5. Preprint on arxiv.org: click here
   6. Preprint on SSRN: click here
   7. Preprint on Research Gate: click here

2. A Theorem on Numbers of the Form 10^x,
   DOI Number: 10.51483/IJPAMR.1.1.2021.55-57

   Abstract: Number theory is one of the core branches of pure mathematics. It has played an important role in the study of natural numbers. In this paper, we are presenting a theorem on the numbers of form 10^x, where x ∊ Z⁺. The proposed theorem have a major application in computer science. It can be used to predict ‘n’ bits which will always represent more than 10^x total numbers. We proved that the nature of the ‘n’ bits is always one of the forms 10i, 10i + 4, or 10i + 7, where i ∊ Z⁺.

   Proposed Theorem:
   
   2^{(10⌊x/3⌋+4((x mod 3) mod 2)+7⌊(x mod 3)/2⌋)} > 10^x ; ∀ x ∈ Z⁺. Here, x is any positive integer.

   Cite as: Ravin Kumar (2021). A Theorem on Numbers of the Form 10^x. International Journal of Pure and Applied Mathematics Research, 1(1), 1-3. doi: 10.51483/IJPAMR.1.1.2021.55-57.

   Resources:
   

   1. Published paper: click here
   2. Published paper (DOI Link): click here
   3. Paper on github.com: click here
   4. Paper on archive.org: click here
   5. Paper on Research Gate: click here
   6. Preprint on SSRN: click here
   7. Preprint on osf.io: click here
   8. Preprint on Research Gate: click here
   9. Github repository (python code): source code

3. Theorems for Arcs of Different Circles having Same Arc-Angles with Application in Concave and Convex Structures,
   DOI Number: 10.51483/IJPAMR.3.1.2023.46-51

   Abstract: Arcs are one of the fundamental concepts of circles and are also used in real-life objects such as bridges, jewelleries, buildings, tools etc. In this paper we have proposed theorems for arcs of different circles having the same arc-angles. The proposed theorems have applications in concave/convex surfaces such as lenses and mirrors, buildings, infrastructures, bridges, jewelleries, and mechanical tools such as a sickle.

   
   

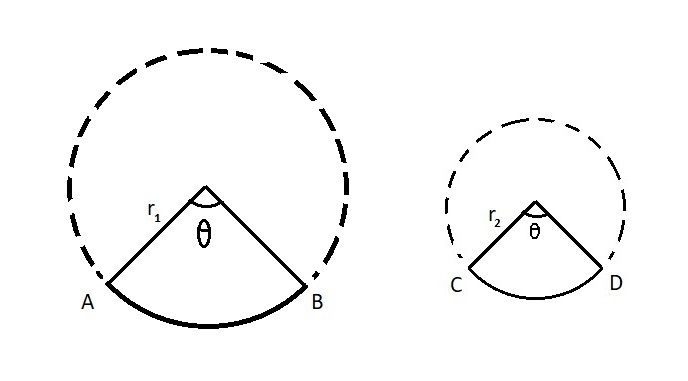
   Figure 1: Circles with arcs of the same arc-angles.
   
   Proposed Theorems:
   
   We have proposed three theorems for arcs from different circles with the same arc angle Θ (in degree unit) along with their mathematical proofs.
   
   
   1. Arc and Chord Length Theorem: Arcs AB and CD having same arc-angles taken from circles with radius r₁ and r₂ respectively. The ratio of the arclengths is equal to the ratio of the line segments obtained after joining the endpoints of the individual arc.
      
      $\frac{\text{Arc Length AB}}{\text{Arc Length CD}} = \frac{\text{Chord Length AB}}{\text{Chord Length CD}}$
      
   
   
   2. Arc and Area Theorem: For arc AB and arc CD having same arc-angles taken from circles with radius r₁ and r₂ respectively. The ratio of the areas enclosed after joining the endpoints of the individual arcs (by a line segment) is equal to the square of the ratio of their individual arc-lengths.
      
      $\frac{\text{Area enclosed by Arc AB and Chord AB}}{\text{Area enclosed by Arc CD and Chord CD}} = \left( \frac{\text{Arc Length AB}}{\text{Arc Length CD}} \right)^2$
      
   
   
   3. Arc Ratio Theorem: For arc AB and arc CD having same arc-angles taken from circles with radius r₁ and r₂ respectively. The following mathematical expression is always true:
      
      $\frac{\text{Area enclosed by arc AB and chord AB}}{\text{Area enclosed by arc CD and chord CD}} = \left(\frac{\text{Arc Length AB}}{\text{Arc Length CD}}\right)^2 = \left(\frac{\text{Chord Length AB}}{\text{Chord Length CD}}\right)^2$
      

   Cite as: Ravin Kumar (2023). Theorems for Arcs of Different Circles having Same Arc-Angles with Application in Concave and Convex Structures. International Journal of Pure and Applied Mathematics Research, 3(1), 46-51. doi: 10.51483/IJPAMR.3.1.2023.46-51.

   Resources:
   

   1. Published paper: click here
   2. Published paper (DOI Link): click here
   3. Paper on github.com: click here
   4. Paper on archive.org: click here
   5. Paper on Research Gate: click here
   6. Preprint on SSRN: click here
   7. Preprint on osf.io: click here
   8. Preprint on Research Gate: click here