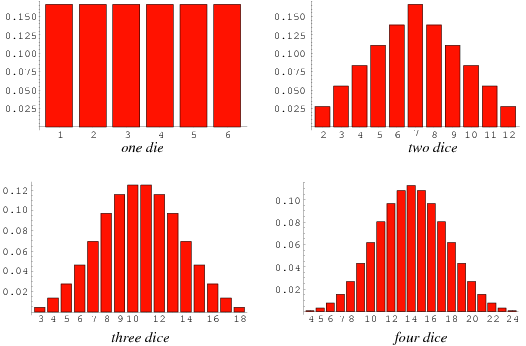
Geometric explanation for most probable sum of three dice
This program is interactive and was written in python with matplotlib.
The plane x + y + z = k (where x, y, z are the individual dice rolls and k is their sum) intersects the sample space
Ω = {{1, 2, 3, 4, 5, 6} x {1, 2, 3, 4, 5, 6} x {1, 2, 3, 4, 5, 6}}, represented by a 3D lattice of points.
- Each lattice point is an event (x, y, z)
- Sums are color coded, with the similarly colored points lining up in planes parallel to x + y + z = k
- k has a slider to offset the plane to a new sum
- Number of intersections (stars) directly determines the probability of the sum
(P(k) = intersections / 63 since all lattice points are equally likely) - Plane cross sections form triangles for k ≤ 8 and k ≥ 13; hexagons in between
- The most intersections occur on the planes where k = 10 or k = 11
Feel free to run the program and view the plot from plenty of angles to understand why the cross section takes on different shapes for different values of k.
For a more detailed explanation, see below . . .
Preview
Click to expand!
If you've ever played Catan, you would know that the most probable sum is 7, since it can occur the most ways. However, a geometric argument would be that the line
x + y = 7
intersects the sample space Ω = {{1, 2, 3, 4, 5, 6} x {1, 2, 3, 4, 5, 6}}
at the most lattice points (6 out of 62, where each is equally likely for fair dice).
Image credit: Professor Hanbaek Lyu
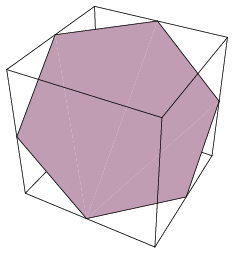
A seemingly likely solution would be the plane
x + y + z = 8
because it intersects the sample space at three vertices of the cube (1, 1, 6), (1, 6, 1), (6, 1, 1): a sum of 8,
The cross section forms a triangle with maximum area. For k < 8, the triangles are closer to the vertex (1, 1, 1), and therefore contain less area, implying that they contain less lattice points than when k = 8.
However, according to Wolfram Alpha, 10 and 11 are the most likely sums for 3 dice!
I created this plot to determine why the seemingly symmetrical answer of 8 was incorrect.
After observing the plot from many angles, I concluded that a hexagonal cross section intersects more lattice points than a triangular one. The 6 edges of the hexagon connect lattice points better than the triangle's 3. Where the k = 8 triangle had a vertex, the k = 10 and k = 11 hexagons have sides that cross the top and bottom faces of the box.
Click to expand!
In the corresponding homework question, Professor Lyu introduced an alternative approach to this question, which generalizes well for n dice.
This method is computationally feasible and does not involve higher dimensional geometry.
Consider the following identity
(x + x2 + x3 + x4 + x5 + x6)3
= x18 + 3x17 + 6x16 + 10x15 + 15x14 + 21x13 + 25x12 + 27x11 + 27x10 + 25x9 + 21x8 + 15x7 + 10x6 + 6x5 + 3x4 + x3
The following are equivalent:
- coefficient of xk
- number of intersections between Ω and the plane x + y + z = k
- number of 3 dice arrangements that sum to k
To connect the polynomial expansion to the geometric interpretation (and therefore the dice arrangements) . . .
Compute the cube of (x + x2 + x3 + x4 + x5 + x6) by summing the products on a 3D grid with each axis labeled with ticks from x to x6. Recall the power rule: xm * xn = xm+n
e.g. point (x, x3, x2) becomes the product x1+3+2 = x6
Finally, group like terms (same power of x), analogous to counting the intersections with matching sums. Note that the coefficients of the expansion sum to 216 (63) as expected.
Thus, the algebraic and geometric interpretations are equivalent.
For a general n, expand the generating function (x + x2 + x3 + x4 + x5 + x6)n
To learn more, look here, here, or here